二维VOBr2 单层的结构畸变及其磁性和铁电性
宋蕊 王必利 冯凯 王黎 梁丹丹
(陆军工程大学基础部,南京 211101)
借助第一性原理计算,对VOBr2 单层的结构、磁性以及铁电性进行了系统研究.计算结果表明低温下VOBr2 会产生自发铁电极化,从高对称顺电相转变为铁电相结构.与同族姊妹材料VOI2 不同的是,V 的二聚化现象不仅无法在VOBr2 中稳定存在,还会导致局域磁矩淬灭.此外,VOBr2 易磁化轴在面内a 轴方向,面内a,b 轴上近邻磁矩均为反铁磁耦合.VOBr2 中的铁电极化主要由V 在a 轴方向V—O—V 链上的铁电位移产生,大小约为40 μC/cm2.与铁电同步翻转相比,通过分步翻转不同链上的铁电极化,可以有效降低铁电翻转能垒,从而有望通过低能外场实现部分或个别链上的铁电翻转,为低能耗高密度铁电存储器件设计提供新的思路和方向.
1 引言
随着21 世纪初单原子层石墨烯的成功制备[1],二维层状材料受到了广泛关注,相关研究热潮很快席卷全球.二维范德瓦耳斯材料的层内具有较强的键合作用,层间则通过较弱的范德瓦耳斯力相互耦合,因而具有易于分层解离的特点.随着相关研究的不断深入,二维范德瓦耳斯材料展现出诸多不同于块材的优异物理性能,加之材料易于制备、比表面积高等特点,为后续二维磁性、铁电性以及量子反常霍尔效应等领域研究起到了推波助澜的作用,掀起了研究的热潮[2-7].随后,在单层SnTe 中发现的铁电性[8]和在单层CrI3,以及多层Cr2Ge2Te6中发现的本征磁性[9,10]又为二维材料、功能材料的研究和磁电器件设计注入了新的活力.
多铁材料同时具有铁电性和磁性,其背后的物理机制和巨大的应用潜力始终吸引着众多研究者的关注.然而经过多年的研究,发现受制于磁性和铁电性的不同机制起源,多铁性材料在自然界非常稀少[11].随着二维材料的兴起,二维多铁的探索之旅也随之开启[12,13].近期的理论报道预测VOX2(X=Cl,Br,I)系列材料中存在着多铁性[14],随后又对VOI2单层材料中的磁性和铁电性展开研究[15,16].然而,关于同一系列材料中的其他成员的研究报道却十分有限[17].本文通过第一性原理计算研究了单层VOBr2材料的结构、磁性和铁电性,结果表明单层VOBr2是具有反铁磁序的离子位移型铁电材料,近邻V4+离子上的局域磁矩在VOBr2面内a,b轴方向均为反铁磁耦合.材料的铁电极化主要源于V 在a轴V—O—V 链方向上的铁电位移,该面内铁电极化大小为39.6 μC/cm2.
2 计算方法
采用基于密度泛函理论的第一性原理计算软件(Viennaab initiosimulation package,VASP)完成计算[18,19].具体采用广义梯度近似(GGA)的Perdew-Burke-Ernzerhof 函数对电子与电子之间的交换关联作用进行处理[20].在单层VOBr2单胞和2 ×2×1 超胞的计算过程中,分别在布里渊区内以Gamma 点为中心采用Monkorst-Park 法[21]取11×11×1 和5×5×1 的K点网格进行积分求和,平面波截断能设为500 eV.晶体结构几何优化迭代的能量收敛判据为1.0×10—5eV,原子力收敛判据为0.01 eV/Å (1 Å=0.1 nm).计算所用单层模型均采用厚度为15 Å的真空层,以避免层间耦合作用的影响.材料的声子谱计算采用DFPT 方法[22],分析处理借助Phonopy 完成[23],铁电极化计算采用Berry Phase 方法[24,25].
3 结果及讨论
3.1 结构分析
首先从具有高对称性的顺电相展开研究.单层VOBr2顺电相结构如图1(a)所示,其中V—O—V 键角为180°,V—Br—V 键角为90°,且V—O,V—Br 键长均各自相等,结构具有中心反演对称性(属于Pmmm空间群).由于Br/O 阴离子半径存在显著差异,导致V—Br 的键长(2.54 Å)明显长于V—O 键(1.81 Å),因此在VO2Br4八面体中,VBr4面内与VO2面外不等价的晶体场作用会导致三重简并的t2g轨道进一步劈裂成具有更低占据能的dxy轨道和能量略高且双重简并的dxz和dyz轨道.如图1(b)内插图所示,dxy轨道躺在xy(VBr4)面内,与z轴(V—O 键)垂直,很难与O 的p 轨道形成交叠,由此不难推断V 的dxy轨道与O 的p轨道之间耦合作用非常微弱.此判断可从VOBr2单层的轨道投影能带图(图1(b))中得到印证.此外,从态密度(DOS)分布(图1(c))不难看出,费米面附近态密度主要源自V 和Br 的贡献,而由于O 的氧化性强于Br,其2p 轨道态密度主要局域于—1 eV以下的内层能级区域,与V 的d轨道没有交叠.因此虽然VOBr2不符合d0规则[11],但当V 在z方向发生铁电位移时并不会受到该d 电子的阻碍[14].
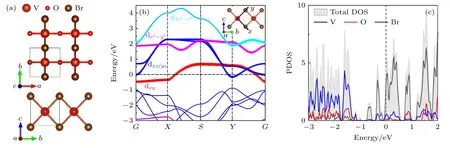
图1 Br2 单层高对称结构示意图(a)、轨道投影能带图(b)、态密度分布(c)Fig.1.(a)Structure diagram,(b)orbital-projected band,and (c)projected DOS of VOBr2 monolayer with high symmetry.
为研究材料的铁电畸变模式,对顺电相VOBr2的2×2×1 超胞进行了声子谱计算,结果见图2.高对称性下材料声子谱存在多个虚频,表明该顺电相结构在零温下并不稳定.借助AMPLIMODES软件[26,27]分析获知这些虚频分别对应S3—,Y1+,Y2+,Γ3—振动模式,即两种V-V 二聚化(Dim1,Dim2)畸变模式和铁电(FE)、反铁电(AFE)畸变模式.其中二聚化结构畸变主要体现在V 离子沿b轴方向的反向位移,两种二聚化模式主要区别在于同一条V—O—V 链上近邻V 之间位移是否同向.如图2(b)和图2(c)所示,同向位移对应Dim1 模式,反向位移对应Dim2 模式.FE 和AFE 畸变模式中V—O—V 链上V 的位移始终都是同向的,两者区别体现在V—Br2—V 链上的近邻V 之间沿a轴的位移方向是否相同,相同则为FE 模式,相反则是AFE模式,具体如图2(d)和图2(e)所示.显然,4 种畸变结构中,只有FE 相结构存在宏观铁电极化.

图2 (a)单层VOBr2 高对称相下2×2×1 超胞的声子谱;(b),(c)声子谱虚频对应的两种二聚化畸变模式Dim1 和Dim2;(d),(e)声子谱虚频对应的两种铁电畸变模式FE 和AFEFig.2.(a)Calculated phonon spectrum of high symmetry VOBr2 2×2×1 supercell;(b),(c)two dimerization distortion modes Dim1 and Dim2;(d),(e)FE and AFE distortion modes,corresponding to the imaginary frequencies in the phonon spectrum.
分别计算上述4 种结构的声子谱,结果如图3所示.其中FE 和AFE 结构相声子谱均是在各自磁基态下进行的,关于体系磁性的分析将在下文展开详细讨论.结果表明,除FE,AFE 结构外,Dim1和Dim2 结构的声子谱均存在虚频.为进一步确定VOBr2的低温基态构型,对Dim1 和Dim2 结构的声子谱虚频进行模式分析,得到了4 种新的畸变结构:FE1,FE2,AFE1 和AFE2,分析结果及相应结构如图4(a)所示.不难发现,其中FE1 结构是FE 畸变与Dim1 畸变模式叠加的结果,FE2是FE 与Dim2 畸变叠加的结果.类似地,AFE1和AFE2 结构是AFE 分别与Dim1 和Dim2 畸变累加的结果.
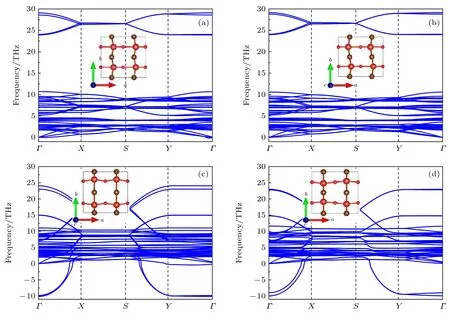
图3 4 种畸变结构的声子谱 (a)FE 相;(b)AFE 相;(c)Dim1 相;(d)Dim2 相Fig.3.Calculated phonon spectrum of the four structural phases:(a)FE;(b)AFE;(c)Dim1;(d)Dim2.
有趣的是,继续对上述4 种畸变结构进行优化时,FE2 和AFE2 中的Dim2型二聚化模式退化消失,结构又分别回到FE 和AFE 相,而FE1 和AFE1 结构的畸变特征在优化后依然存在.后续的声子谱计算(图4(b))表明,FE1 和AFE1 结构均没有虚频,说明这两种结构与FE 和AFE 相一样都是VOBr2的可能构型.但是通过能量对比发现,FE 相能量是4 种结构中最低的(见表1),由此可见,FE 相才是VOBr2的低温基态结构,而另外3 种结构都是VOBr2的亚稳态构型.

表1 含磁优化结果对比汇总表Table 1. Summary of the main results of structural and magnetic optimization.

图4 (a)单层VOBr2 2×2×1 超胞的畸变模式分析;(b)FE1 和AFE1 畸变结构的声子谱Fig.4.(a)Distortion mode analysis of 2×2×1 super cell of VOBr2 monolayer;(b)calculated phonon spectra of VOBr2 monolayer in FE1 and AFE1 distortion modes.
3.2 磁性研究
考虑到VOBr2中V4+离子外层有一个未配对的3d 电子,对FE,AFE,FE1,AFE1 四种结构相进行了含磁优化计算,其中考虑了4 种常见磁序(图5(a)).具体计算结果如表1 所列.
结果显示,含磁优化后FE 结构的磁基态能量最低,AFE 相的基态能量次之,两种结构相在各自磁基态下的局域磁矩分别为0.96μB和0.98μB,与V4+离子外层3d1的电子配置(S=1/2)相吻合,并且与VOI2中的结果一致[14,15].不同的是,FE结构相下VOBr2的磁基态为GAFM,即a轴和b轴上近邻V 离子间自旋均为反平行排列(如图5(a)所示).其中b轴上近邻V 离子间存在V-V直接磁交换作用和以Br 为媒介的超交换作用,前者倾向于反铁磁耦合,而根据Goodenough-Kanamori规则后者倾向于铁磁耦合,显然直接交换作用在竞争中占据主导地位[28,29].此外,亚稳态的aFbA 磁序仅比基态GAFM 高了1 meV/f.u.,预示着a轴方向上的磁耦合相对较弱.

图5 (a)含磁优化计算考虑的4 种常见磁序:FM 表示近邻V 离子自旋平行排列,即铁磁序;aAbF 表示近邻V 离子自旋沿a 轴反平行排列,沿b 轴平行排列;aFbA 表示V 离子自旋沿a 轴平行排列,沿b 轴反平行排列;GAFM 表示近邻V 离子间自旋均反平行排列;(b)FE 相GAFM 磁基态下的投影态密度分布Fig.5.(a)Four magnetic orders considered in the magnetic ground state calculations.FM denotes the spin parallel arrangement,aAbF denotes the antiferromagnetic (ferromagnetic)coupling between neighbouring V ions along a (b)-axis,aFbA represents the ferromagnetic (antiferromagnetic)coupling along a (b)-axis,and GAFM denotes the antiferromagnetic coupling between neighbouring V ions along both directions.(b)Projected DOS of the GAFM ground state within the FE structural phase.
根据Mermin-Wagner 理论,长程磁有序无法在各向同性的二维体系中稳定存在.为确认VOBr2单层中存在长程磁序,对材料的磁晶各向异性进行计算,与VOI2中情况相同,VOBr2单层的易磁化轴也在面内沿a轴方向[15],面内外的磁晶各向异性能为60 μeV/f.u..
此外,在FE 相的磁基态中,磁有序导致体系打开大小为0.8 eV 的能隙.如图5(b)所示,V 和Br在费米面附近存在较强的轨道杂化,O 的p 轨道依然分布在—1 eV 以下能量区域.借助metaGGA算法针对FE 相的GAFM 磁基态做了进一步验算,所获得的能隙为0.7 eV 与密度泛函理论结果吻合.
与FE,AFE 结构不同,沿b轴方向的V-V 二聚化导致FE1 和AFE1 结构的b轴明显收缩,能隙也有所减小.而且两者的含磁优化输出磁矩均为零,不同初始磁序的最终收敛能量都完全相同.该现象可以理解为,V-V 二聚体内两个3 d 电子归二聚体共有并形成配对,从而导致局域磁矩为零,体系呈现出非磁性.事实上,TiCl3,MoCl3以及TcCl3体系中均存在由于金属离子二聚化导致局域磁矩淬灭的实验现象和理论报道[30-32].
3.3 铁电性研究
为研究材料的铁电性,采用Berry Phase 方法对FE 相VOBr2的极化大小进行了计算,结果表明VOBr2铁电极化沿a轴即V—O—V 链方向,主要源于V 离子在该方向上的铁电极化位移.如图6(a)所示,VOBr2铁电极化大小为277.5 pC/m,若按照单层VOBr2厚度为7.0 Å来换算,可折算为39.6 μC/cm2,与点电荷模型估算值33.6 μC/cm2较为吻合.该数值与本征钙钛矿铁电BaTiO3的极化大小相近[33],同时也与文献[14]报道的VOX2系列材料中的相关数据相符.
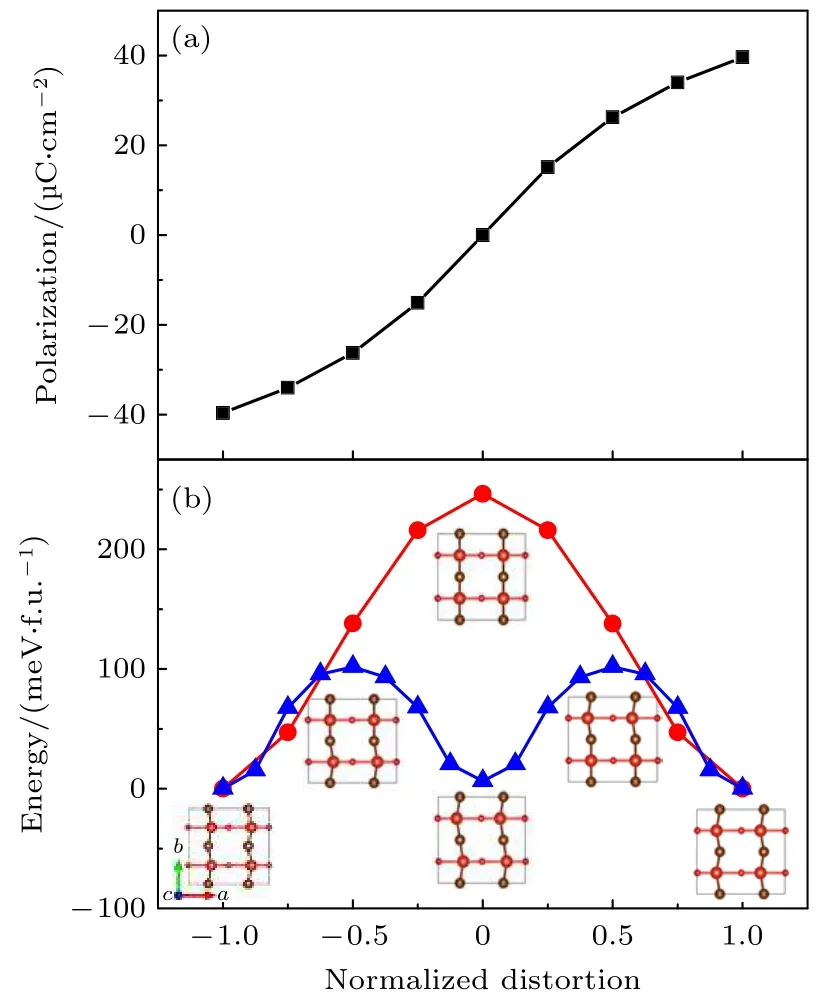
图6 (a)单层VOBr2 的铁电极化;(b)两种铁电翻转路径下的能垒,红色表示途径PE 的路径,蓝色对应途径AFE的翻转路径Fig.6.(a)Polarization of VOBr2 monolayer.(b)Energy barriers of two ferroelectric flipping paths:FE-PE-FE (red)and FE-AFE-FE (blue).
接下来估算了VOBr2的铁电翻转势垒.从FE极化相出发,考虑V—O—V 链上所有V 离子沿a轴同向位移,经过顺电相实现铁电极化从—P到+P 的翻转.该过程对应的能量曲线如图6(b)中红色曲线所示,对应的铁电翻转能垒为246 meV/f.u.,该数值与传统钙钛矿铁电PbTiO3材料的翻转能垒(约220 meV/f.u.)相近[34].为有效降低该翻转势垒,又模拟了途径AFE 相的翻转路径,即考虑近邻V—O—V 链上V 离子的极化翻转并非同步发生,而是分步进行:首先彼此相互间隔的半数V—O—V链上的V 先发生铁电位移翻转,导致近邻V—O—V链间极化相反,此时材料从FE 相转变为AFE 相;随后另半数V 再发生相同的铁电翻转,从而实现从—P 态到+P 态的转换(具体过程如图6(b)中蓝色曲线及其附近插图所示).不难看出,该路径的能垒显著降低至100 meV/f.u..由此可推测,实际应用中可以通过更低能的外场调控实现局部少数V—O—V 链甚至是单链上的铁电翻转,从而可以在提高铁电存储器数据密度的同时有效降低能耗.
4 结论
通过密度泛函理论计算,系统地研究了二维VOBr2单层的低温结构相、磁性以及铁电性.结果表明,VOBr2是一种同时具有反铁磁序和铁电性的多铁性材料.材料磁性源自V4+离子外层未配对的3d1电子,磁基态下近邻V 位上局域磁矩呈反铁磁耦合.此外,受到VO2Br4八面体的晶体场劈裂作用影响,V4+离子外层d 电子主要占据dxy轨道,使得V,O 间的d-p 轨道耦合十分微弱,并不会阻碍V 在z方向(V—O—V 链上)的铁电位移,导致材料呈现出违背d0规则的本征铁电性.更有趣的是,由于二维VOBr2本征的低维特性,有望通过较小能量的外场调控实现个别V—O—V 链上的铁电翻转,这无疑为铁电存储器件设计应用提供了更多思路,其中的诸多物理性质有待后续更深入的探究.

