基于多径信道模型研究时间反演腔的反演特性

陆希成 邱扬† 田锦 汪海波 江凌 陈鑫3)

1) (西安电子科技大学机电工程学院,西安 710071)

2) (西北核技术研究院,西安 710024)

3) (中国工程物理研究院电子工程研究所,绵阳 621999)

基于时间反演腔的电磁波时间反演技术在许多方面有着潜在的应用,如脉冲压缩、功率合成、微扰探测、波束成形等.其中,时间反演腔通常采用具有多径传输特征的微波混沌腔.利用衍射理论,虽然可以证明这类腔体在时间反演过程中具有时空聚焦特性并可用于脉冲压缩,但是它不能用于分析腔体的反演性能.为了得到一个合适的分析方法并可用于指导时间反演腔设计,本文基于信道理论,分析电磁波传播的散射、扩散和衰减特性,构建了时间反演腔的多径信道模型,并详细研究了路径之间的串扰特征,给出反演重构信号的时间旁瓣产生机理、时移特征以及对主瓣的干扰情况.另外,根据随机平面波假设,还分析了空间焦斑的分布特征.实际焦斑大小不但受限于衍射极限而且还与初始焦斑大小有关.这些理论分析结果与实验和数值仿真结果基本一致.

1 引言

时间反演方法是将系统响应信号进行时间翻转后形成反演信号,然后再输入到系统中,并在初始位置重构出原始波形的一种方法,该方法具有时空同步聚焦特性.早在20世纪六七十年代,人们就提出了时间反演的概念[1],主要用于研究声波在时间和空间上的聚焦[2].在数学上,声波的传播方程与电磁波的传播方程是一致的,均为双曲型扩散方程.因此,理论上可将声学中的时间反演技术引入到电磁学领域.直到2000年之后,随着高频数字采样技术的成熟,时间反演技术才开始引入到电磁学领域.第一个电磁反演系统由单个收发天线和高Q值混响室(即时间反演腔)组成[1].该系统采用的时间反演腔(time reversal cavity,TRC)不但可以提高时间反演中的多径效应,而且还克服了收发天线的时空覆盖限制,具有很好的反演性能.对于TRC,一些研究人员利用衍射理论和格林函数证明了时间反演的时空聚焦特性[3,4].

近年来,许多研究人员开展了TRC的时间反演技术在脉冲压缩及功率合成[5−7]、保密通信[8−10]、反演成像[11,12]、波束成形及定位[13−17],微扰探测[18,19]等方面的理论和实验研究.为了进一步推进实际应用,还需要建立合适的物理模型和方法,用于分析TRC的反演性能并指导TRC的优化设计.但目前还缺少这方面的深入研究.当前主要是采用无线信道理论中的统计建模和确定性建模的仿真方法开展分析.例如,文献[20]基于样本参数信息采用遗传算法优化的神经网络模型方法去获得质量较好的反演系统;文献[21]利用数值仿真分析了无线信道的时间反演多径特征.但在TRC的优化设计中,改变参数就需要重新仿真计算.该方法不但耗时长,而且也很难指导获得最优结构.

本文将基于多径信道理论,分析路径之间的串扰特征,建立TRC的多径信道模型,并用于分析TRC重构信号的时间主瓣与旁瓣特征.此外,假设路径上传播的电磁波为随机平面波,进一步分析重构信号的空间分布.这些可为TRC优化设计和实际应用提供理论支持.

2 多径信道模型

2.1时间反演腔

当电磁波传输介质的介电常数和磁导率张量均为实对称矩阵时,电磁系统具有时间反演对称性,也称为时间反演不变性[22].基于这种对称性,文献[1]中构建了一个TRC系统,并开展了电磁波的时间反演实验,其典型结构如图1所示.其中,系统中的TRC满足电大条件(电大条件是指腔体特征尺寸远大于传播波长的情况);Port 0和Port 1为系统的输入或输出端口.另外,上部蓝线为普通的响应过程,下部红线为反演过程.

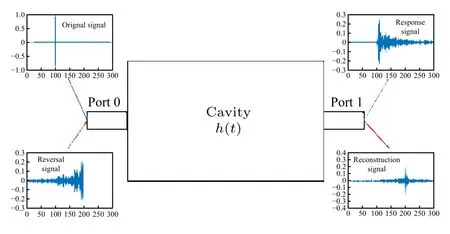
图1 典型的TRC系统Fig.1.Classical TRC system.

该系统中的电磁波从一个端口经腔体传播到另一个端口.根据信息论,该通道能够传送信息(电磁波),可认为是一条完整的信道.由此,本文利用信道的概念和理论来分析TRC系统的时间反演问题,并将Port 0,Port 1和TRC构成信道的冲激响应函数利用h(t) 表示.

为了简化分析,本文以电场信号为例分析电磁时间反演的特性.并且,进一步将电场矢量信号简化为标量信号,记为s(t) .在这种情况下,如果初始信号sori(t) 在Port 0输入,则在Port 1的响应信号sres(t) 可表示为

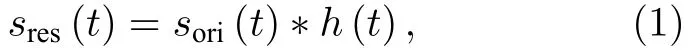
式中,∗为卷积算符.将响应信号进行时间反演变换可得到反演信号srev(t) 为

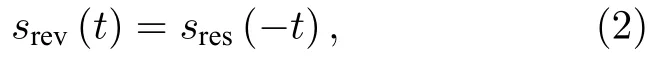
并将其在Port 0(或Port 1)输入到系统中.由此,可以得到时间反演重构信号srec(t) 为

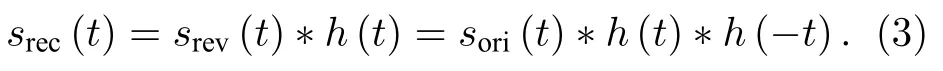
为了研究反演重构信号的特征,需要重点分析冲激响应函数.由此本文定义它的自相关函数κ(t) 为

它是决定系统时间反演性能的一个核心参数.在理想条件下,系统的自相关函数满足

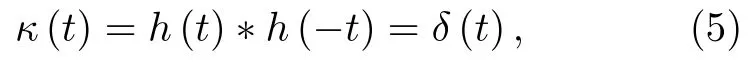
式中,δ为奇异函数.此时,重构信号等于初始信号,即srec(t)sori(t) .

但在实际情况下,电磁波传播的扩散、散射和衰减特性将会导致自相关函数并不等于奇异函数.也就是说,实际情况下反演重构信号并不完全等于初始信号,如图2所示.该重构信号是基于图1中的几何模型通过实验方法获得的,具体反演过程也可参见图1.

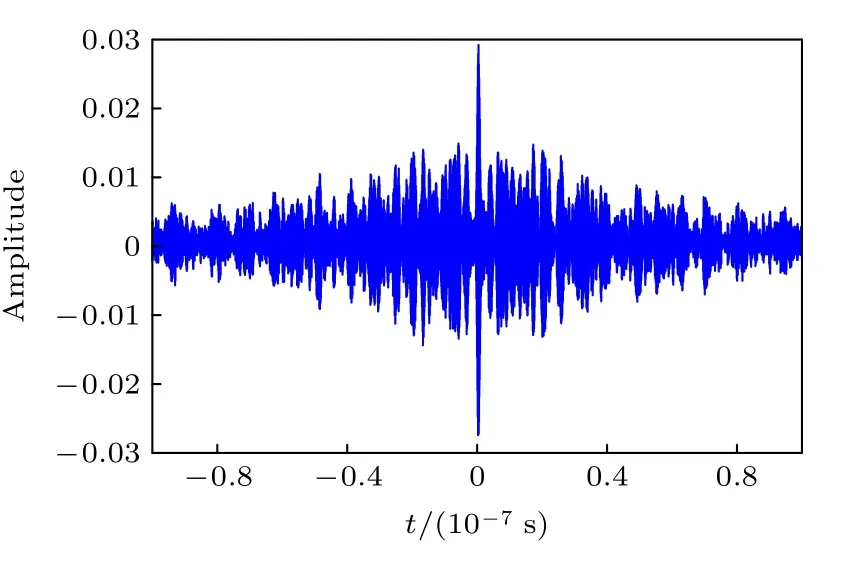
图2 实验测量的时间反演腔重构信号Fig.2.Reconstructed signal of TRC.

另外,从数学上看,时间反演过程等于系统分别进行了一次卷积和一次反卷积运算.因此,时间反演系统也可称为卷积系统.

2.2 多径串扰

对于电大的TRC,腔体内电磁波的传播满足程函近似条件,即波长变化缓慢并且振幅的变化远小于相位的变化,可近似认为是无穷多个相互独立的射线形式传播[23].因此,TRC系统可看成是一个多径信道,冲激响应函数h(t) 可通过多径信道理论来建模.信道中的多径可能包括了直射路径、散射路径(镜面散射和漫散射)、衍射路径、绕射路径等.他们有长有短,信号到达接收端的时间会不同,将会出现多径时延现象,即时间色散特征.

如果仅从空间上看,信道内每条路径都是相互独立的,具有独立的冲激响应函数.在线性条件下,信道的冲激响应函数h(t) 可表示为信道内每条路径的冲激响应函数hi(t)之和,即h(t) 可表示为

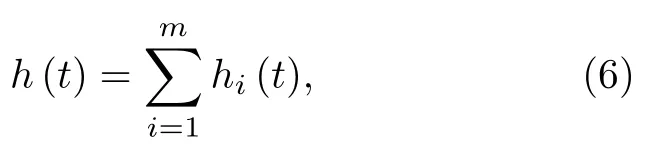
式中,m表示信道的所有路径数量.

虽然在空间上腔体内的路径是相互独立的,但是由于电磁波在传播过程中的扩散特性和散射特征,将会导致不同路径上传播的电磁波出现串扰(互耦)现象,如图3所示,即独立路径上的电磁冲激响应函数hi(t) 不再独立.由此,本文重新定义多径信道的冲激响应函数为

图3 散射和扩散对路径串扰影响 (a) 散射情况;(b) 扩散情况Fig.3.Crosstalk of scattering and diffusion on paths:(a) Scattering;(b) diffusion.

式中,k(t) 为路径的衰减系数向量,其第i个系数ki(t)描述了第i条路径上传播信号的时间衰减特征;矩阵A(t) 为电磁波在每条路径之间传播的关联矩阵,描述了路径之间电磁波传播的串扰特征,可表示为

其中,aij(t) 表示第i条路径上的电磁波传播到第j条路径上的相关性.δ为奇异函数向量,可表示为

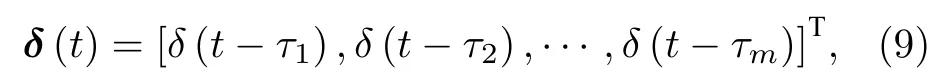
其中,τi为第i条路径的响应延迟时间(即路径的飞行时间);T表示向量的转置.

3 反演特性分析

根据多径信道模型可知,路径将会对反演信号进行时间补偿,使得沿不同路径传播的信号同时到达接收端口,可重构出初始信号.在这个过程中,电磁波出现了时间和空间上的汇聚,即具有时间压缩和空间聚焦特征.这也是时间反演技术两个最重要的基本特性.

但是,电磁波在路径之间的传播存在串扰使得反演重构信号出现“噪声”,导致重构信号与初始信号并不完全相同.另外,从空域上看,由于电磁波的衍射特征,也会导致重构信号的空间分布不可能与初始信号分布一致.由此,本文根据重构信号分析它的反演特性.

3.1时域波形特征

3.1.1 主瓣与旁瓣

根据多径信道模型,自相关函数κ(t) 和重构信号srec(t) 可分别表示为

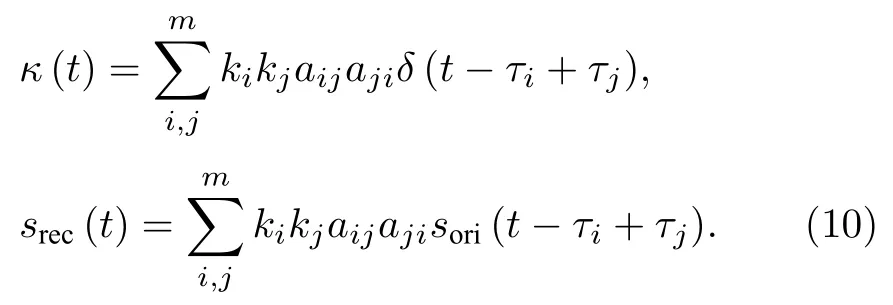
根据关联矩阵特性,可将(10)式分成以下几种情况讨论.

1)当ij时,有τiτj,自相关函数和重构信号可表示为

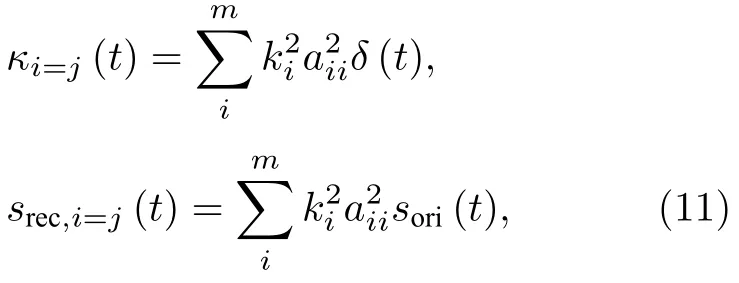
式中,κi=j(t) 表示第i条路径自身传播电磁波的相关特性.由此可见,在ij时,重构信号srec,i=j(t)与初始信号波形一致,只是幅度减小了.这种情况没有考虑到串扰的影响.

2)当ij时,若τiτj,自相关函数和重构信号可表示为

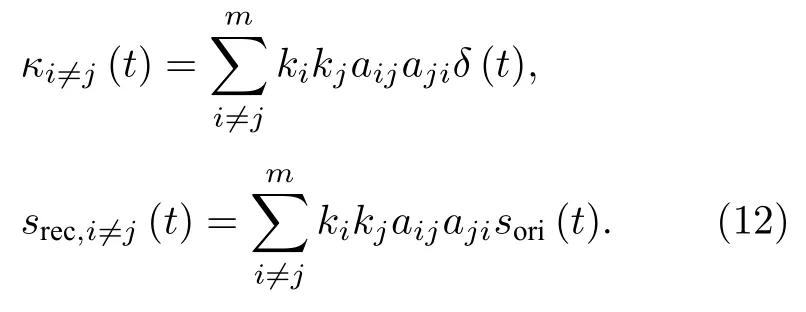
此时,重构信号的波形与初始信号波形也一致.由此,可将同时到达的路径认为是同一个路径,这在路径的时间分析中非常有利.

3)当ij时,若τiτj,自相关函数和重构信号可表示为

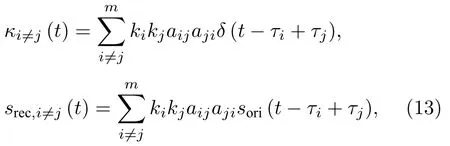
式中,κi=j(t) 表示第i条路径和第j条路径上电磁波传播的相关性.在电磁波传播的扩散和散射特性条件下,aij0和aji0.此时,重构信号srec,i=j(t)的波形与初始信号波形基本一致,只是出现了时间偏移 (τi−τj) .

由此,重构信号中发生时间偏移的信号被称为“时间旁瓣”,而第一部分中没有出现时间偏移的信号,则称为“时间主瓣”.再根据电磁波传播的对称性可知,关联矩阵中的单元相关系数应满足

这也反映出反演重构信号的时间旁瓣具有对称性,如图2所示.

如果时间反演系统中没有电磁散射,例如只有直射路径,则路径之间没有信息(能量)交换.此时,重构信号不会出现时间旁瓣,文献[24]给出了实验证实.由此可见,散射是重构信号出现时间旁瓣的一个必要因素.但是,根据电磁场理论可知,系统散射是产生多径的主要原因,电磁波的扩散才是引起路径之间串扰的核心因素.因此,旁瓣应是系统散射和波扩散的共同作用结果.

3.1.2 旁瓣时移

利用射线追踪理论,路径串扰主要发生在发射端口和接收端口.在这种情况下,旁瓣时移可利用不同路径传播的时间差表示,即 (τi−τj) .它能够反映出主瓣和旁瓣、旁瓣与旁瓣之间的时间间隔,可用于区分主瓣的被干扰情况.

根据上述分析,旁瓣时移应与路径长度有关,即路径越长则串扰信号的时移就越大.对于一个TRC,从统计上可将路径分为直接到达路径、第一次反射到达路径、第二次反射到达路径、以及第n次反射到达路径,即将其分成n+1类.在这种情况下,每类路径的时移可用腔体内射线的平均自由飞行时间τc(即平均自由程的射线飞行时间,也称为腔体特征时间常数)来表示.

当收发端口位于腔体两侧时,根据上述分析,第i类到达路径的旁瓣时移τi可近似表示为

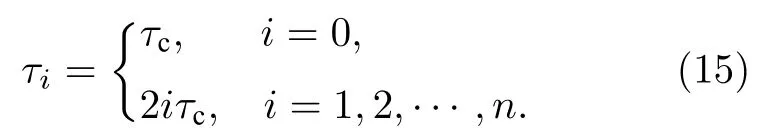
由此,时间旁瓣的相对时移Tij可近似表示为

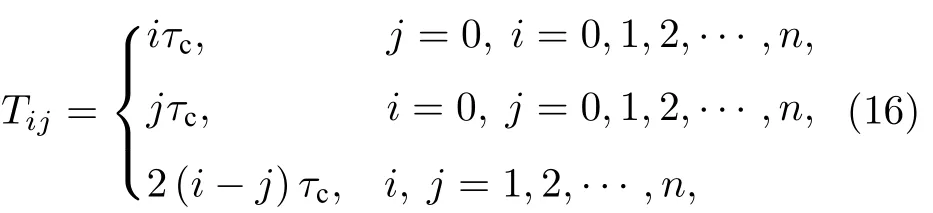
式中,i和j是任意的整数.由此可见,反演的时间旁瓣具有对称性,如图2所示.

根据上述分析,初始信号脉宽大于2倍的腔体特征时间常数时,旁瓣和主瓣将会产生叠加,从而影响主瓣波形,如图4所示.仿真模型如图1所示,其中TRC尺寸为600 mm × 400 mm,特征时间常数约为0.8 ns,初始信号为载波频率10 GHz脉宽10 ns的方波脉冲.由此可见,主瓣受到了一定的干扰.根据腔体特征时间常数定义可知,旁瓣时移主要与腔体尺寸有关.这在TRC的选择和初始信号脉宽设计中具有很好的指导作用.

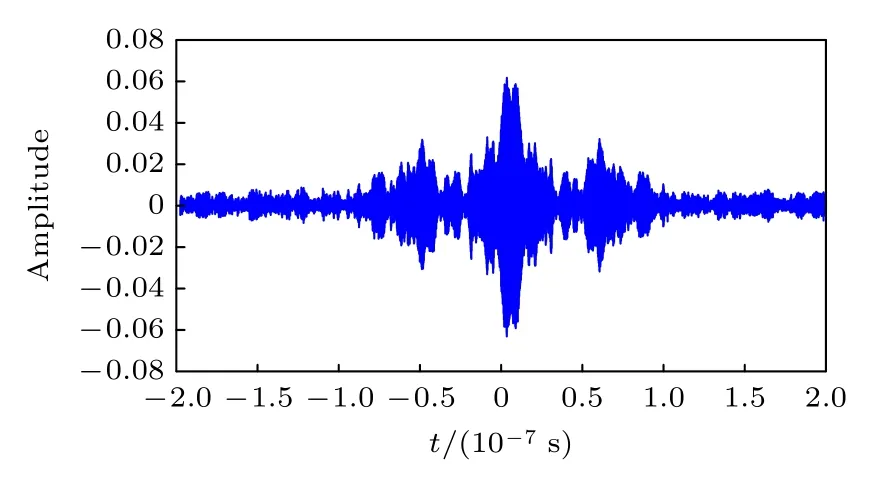
图4 旁瓣对主瓣的干扰Fig.4.Interference of side lobe to main lobe.

3.2 空间分布特征

3.2.1 空间方向图

由于电磁波的衍射特性,时间反演的空间聚焦不会形成一个理想点.由此定义时间反演空间方向图来表示它的空间聚焦特性,即可利用相关函数的主瓣最大值(即t0)垂直于传播方向上的分布表示.以单方向为例,有

式中,D(x) 表示x方向上的分布.

对于TRC,可假设每条路径上传播的电磁波为随机平面波[25].在接收端口位置上的电磁场为这些平面波的线性叠加.根据中心极限定理,电磁场空间分布的相关函数可表示为

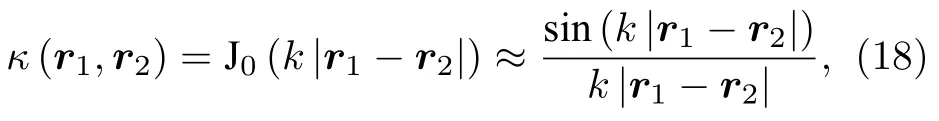
式中,J0为零阶贝塞尔函数;r1和r2表示空间任意两点.该式反映出了系统反演空间聚焦特性,与文献[3]中利用衍射理论得到的结果一致.

当kn|r1−r2|→∞时,两个空间位置的场相关函数趋近于零,即可认为,在远大于一个波长情况下,在点r1的重构信号对点r2的重构信号没有影响.由此,可以得到系统时间反演的空间分辨率等于λ/2,即满足经典衍射极限.另外,如果重构信号端口存在近场散射,则还可获得时间反演的超分辨率特性[26−28].

3.2.2 焦斑分布

实际的空间聚焦尺寸,即焦斑,应是初始信号分布和自相关函数的卷积.由此,初始信号发射时的分布dori(x) 与空间方向图进行卷积,有

式中,d(x) 为重构信号的焦斑分布.由此可见,如果初始发射信号的分布过宽,则会导致重构信号的焦斑过大,不利于能量的空间聚焦.

图5给出了利用(19)式的计算结果和相应的数值仿真结果的比较.其中,仿真计算模型与图1计算采用的模型相同.由此可见,理论分析结果和仿真计算结果基本一致.在系统不满足反演超分辨率的情况下,反演重构信号的焦斑不会小于λ/2 .这可为反演重构信号的能量提取端口设计提供技术支持.

图5 焦斑分布比较Fig.5.Comparison of focal spot distribution.

4 结论

本文根据电磁波传播的散射和扩散特征分析了TRC的多径路径串扰,建立了时间反演腔的多径信道模型.利用该模型,研究了重构信号时间旁瓣的产生机理,给出了旁瓣对主瓣的干扰情况以及旁瓣时移与腔体尺寸(特征时间常数)的关系,即时间反演腔的尺寸越大,则旁瓣时移就越大.该结论可用于指导选择合适的初始信号脉宽或合适的腔体尺寸.另外,根据路径上的随机平面波假设,同样可以得到空间聚焦的最小衍射极限为λ/2 .但实际的反演焦斑不仅仅受限于衍射极限,还与初始端口的电磁场分布有关.这些研究结果对接收端口设计和反演信号的能量提取有重要意义.