黄原胶溶液中法拉第斑图色散关系的修正
高云浩,王 伟,周路群
(北京大学 a.元培学院;b.物理学院,北京 100871)
1831年,法拉第(Michael Faraday)发现,对一定质量的液体施加竖直简谐驱动后,在一定条件下可形成稳定的表面驻波[1],这种现象被称为法拉第斑图(Faraday waves). 法拉第斑图系统是经典的复杂非线性系统,其物理内涵丰富,已有大量有关斑图的实验、理论结果被报道,但是仍有许多问题值得进一步研究.
法拉第斑图系统中稳定模态与连续流体介质中的表面波具有相同的色散关系. 朗道(Lev Davidovich Landau)对纳维-斯托克斯(Navier-Stokes)方程采取了理想流体、纯势流和小振动近似,给出了经典表面重力张力波的色散关系表达式[2]. 基于对黄原胶溶液沿某一直径方向的斑图色散关系的测量,亓瑞时等人在低频区域对朗道的结果进行了较充分的检验[3];然而,在高频驱动下,黏滞耗散和流体本身表现的非线性效应逐渐显著,原色散关系将不再适用,需要进行修正.
本文从黏滞耗散和剪切稀化效应出发,对经典色散关系进行理论修正;实验测量黄原胶溶液在较大频率范围内的色散关系,通过实验验证所作理论修正的合理性.
1 理论分析
在本部分中,首先简要介绍朗道的经典色散关系及处理方法,随后引入黏滞耗散和剪切稀化作用,进行理论修正.
1.1 朗道的经典色散关系
朗道从理想不可压缩流体的欧拉方程出发,设重力加速度为g,流体密度为ρ,得出流体速度场v和压强p的关系
(1)
忽略(v·)v项,将流体视为纯势流v=φ.按z轴竖直向上建立直角坐标系.因为表面张力引起的压强差满足拉普拉斯公式Δp=ακ,其中α为表面张力系数,为表面平均曲率,可得流体表面z=h(x,y,t)处速度势φ满足
(2)
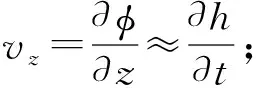
(3)
设流体厚度为H,利用流体底部流速为0的边界条件,结合式(3),即可得到经典表面重力张力波的色散关系为
(4)
其中,ω为频率,k为波矢.
朗道的处理主要采用了3点近似:
a.理想流体近似;
b.纯势流近似;
c.小振动近似.
在下面的分析中,将分别给出对应这3点近似的修正.
1.2 黏滞耗散对色散关系的修正
1.2.1 严格定解方程组
写出决定流体运动的严格定解方程组,其中连续性方程为
·v=0,
(5)
纳维-斯托克斯方程为
(6)

(7)
液面处应力平衡方程为
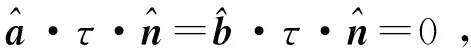
(8)
(9)
式(8)和(9)分别描述了切向平衡与法向平衡.引入黏滞应力张量τ=2ργe=2ηe,其中:
(10)
分析定解方程组[式(5)~(10)]可以看出,黏滞耗散的影响包含两方面:流体的运动方程中需要引入γ2v项,流体表面处的平衡方程需要考虑黏性阻力的作用,二者将分别影响流体运动满足的微分方程和边界条件.
1.2.2 准势流近似和小振动近似
式(5)~(10)不能直接解析求解,原因在于无法做纯势流假设而使方程标量化.在与边界接触(简称边界层)处,流体黏滞耗散的作用将占据主导地位,使得流体不再是有势流.
针对这一问题,引入速度势,使得v=φ,从而简化方程,此处采取的是准势流近似.准势流近似假设流场除了边界层外都是有势的,而在边界层处以适当的关系进行连接[4].得到微分方程
2φ=0 ,
(11)
边界条件为
(12)
(13)
(14)
式中,h=h(x,y,t)为流体表面方程,W=W(x,y,t)为流体表面速度沿z方向的旋转分量.式(11)~(14)为标量形式的定解方程组.
并写出有关h与φ的二元微分方程组
(15)
(16)
其中,φ满足拉普拉斯方程,即式(11).比较式(15)与式(16),可以发现h与φ满足的方程是对称的,因此可用h描述流体的运动.结合式(11),式(15)与式(16)可以消去φ,并化简得到有关h的微分方程为
(17)
式(17)是典型的阻尼振动方程,其阻尼来自黏滞耗散.该式表明黏滞项导致的耗散系数为2γk2.
1.2.3 黏滞耗散对色散关系的修正
式(17)描述的是衰减波,如果系统要产生稳定波,必须引入外界能量输入,这对应于法拉第斑图系统中的竖直简谐驱动.如果以振动的容器为参考系,该驱动等效的重力加速度g随时间谐变,即
g→g[1+εcos (Ωt)],
(18)
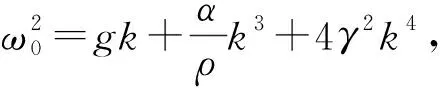
(19)
理论分析表明,当发生稳定共振时,驱动频率恰为本征频率的2倍[6],即
Ω=2ω0,
(20)
在实验上可用式(20)确定ω0.从式(19)出发,略去下标,设流体厚度为H,利用流体底部流速为0的边界条件,可得到振动频率
(21)
在以上过程中,对应于朗道的近似,采取了以下修正:
a.抛弃理想流体近似,引入黏度;
b.将纯势流近似修正为准势流近似;
c.保留小振动近似.
根据式(21),黏滞耗散为色散关系引入了四次方依赖项. 对于恒黏度体系,这个依赖项将在高频下起主导作用.
1.3 剪切稀化效应及其对色散关系的修正
黄原胶溶液是典型的假塑性非牛顿流体,实验表明,黄原胶溶液的黏度随着剪切速率的增大而降低,即存在剪切稀化效应[7],在高频下该效应将弱化黏滞耗散. 一般认为静止或低剪切速率的黄原胶溶液中,黄原胶分子彼此缠绕,形成高黏度;随着剪切速率逐渐增大,黄原胶分子团发生解聚,变为分离的链状结构,因而溶液的黏度不断下降.
流变学中存在多个经验公式描述剪切稀化效应,如幂律方程、Cross方程、Carreau方程等[8]. 其中,幂律方程形式简单,且对于黄原胶溶液符合程度较好,这在文献[7]中已经得到证实.
幂律方程指出,在一定范围内,动力黏度η与剪切速率v之间存在如下关系
η=Kvn-1(0 (22) (23) 式(23)考虑了剪切稀化效应,该效应为黏滞修正提供了负反馈,弱化了黏滞耗散. 实验装置示意图[3]如图1所示. 各仪器的型号为:模态激振器JZK-100,扫频信号发生器YE1311,功率放大器YE5878,压电式加速度传感器GA-YD-107,电荷放大器YE5852(江苏联能电子技术有限公司),示波器TDS1002[泰克科技(中国)有限公司],高速摄像机AOS S-MOTION(瑞士AOS公司). 图1 实验装置示意图 实验中,驱动信号由信号发生器产生,经功率放大器放大,输入模态激振器,使激振器产生竖直方向的简谐驱动,带动固定于其上的平板、加速度传感器以及装有一定量黄原胶溶液的无盖圆形容器;传感器的加速度信号经电荷放大器后输入示波器供读取;高速摄像机用于观察表面形成的法拉第斑图,摄像机下装有均匀照明光源. 实验采用容器的内径D=9.00 cm,注入的黄原胶溶液浓度c=5 g/L,厚度H=2.00 cm. 在此参量条件下溶液的密度ρ=976 kg/m3,表面张力系数α=0.085 N/m. 实验中重力加速度g=9.80 m/s2. 实验中由高至低调节驱动信号频率,观察斑图出现的临界位置,此时应为振幅不大且较为稳定的表面驻波. 通过示波器可以测量驱动加速度信号的频率. 设此时示波器读数为f(单位:Hz),则Ω=2πf. 据式(20)可知此时ω=πf. (a) 23 Hz驱动下的拍摄结果 在具体的图像处理过程中,先将原始图像转换为灰度图像,再通过边缘识别,匹配出等相位点,即可实现自动化测量. 在均匀光源照射下,峰顶点与其周围点存在较大的亮度差异,实验中将峰的匹配模式设定为在圆形深色区域中的浅色点. 在高频的情况下,斑图呈现出高度周期性的特征. 此时可以通过二维傅里叶变换,将灰度图像表征的位置分布变换为空间频谱分布,从而得到较为准确的空间频率,如图3所示. 将通过以上方式测得的ω和k绘制在坐标图中,得到色散曲线. 实验中设置驱动频率范围10~120 Hz,其中大于35 Hz的部分属于高频段. (a) 100 Hz驱动下的拍摄结果(红色圈为液面边缘) 黄原胶溶液的实验结果如图4所示. 黑色数据点为实验的测量结果,蓝色线为朗道经典色散曲线[7],红色线为引入恒定黏度修正的色散曲线,橙色线为在考虑黏度的基础上引入了剪切稀化效应的色散曲线. 图4 黄原胶溶液的色散关系 从图4可以看出,实际色散点整体高于经典色散关系曲线;在较低频段,恒定黏度的修正公式[式(18)]已经给出较为满意的符合结果;随着频率增大,恒定黏度修正显著大于实测结果,这说明此时剪切稀化效应不可忽略,采用剪切稀化修正公式[式(20)]的符合结果较好. 做进一步定量分析,从修正后的色散关系出发,根据测得的多点ω和k值,可以反解出对应的γ(ω)与η(ω)分别为 (24) (25) 作出η(ω)与ω的双对数关系图并进行线性拟合,如图5所示. 图5 黄原胶溶液的动力黏度与频率的关系 根据幂律方程η∝ωn-1,由拟合结果可以得出n≈0.13.文献[7]中给出浓度为5 g/L的黄原胶溶液对应n≈0.2,本实验的结果与其大致吻合.因此,在误差允许范围内,实验与理论修正的结果一致. 在本实验中,边界效应的影响、高阶非线性效应、高速摄像机的中心投影偏差等误差仍然存在.但是根据以上实验结果可以判断,在测量的频率范围内,这部分误差的效应远不及黏滞耗散和剪切稀化效应,且后者对于黄原胶溶液的色散曲线修正起到了主导作用. 从经典表面重力张力波的色散关系出发,基于黏滞耗散和剪切稀化效应,引入了理论修正,提出了适用范围更广的色散关系表达式,揭示了流体的黏滞耗散和流体本身的性质对色散关系的作用. 在黄原胶溶液体系中测定了10~120 Hz范围内的色散曲线,定量验证了理论修正结果. 所得到的色散关系将适用于在较高频率条件下描述其他斑图体系的色散行为. 在表达式推导过程中仍然保留了小振动近似. 实验中观察到,在振幅较大的情况下也能形成稳定的斑图,说明斑图系统中存在丰富的非线性现象. 斑图中更普遍的色散关系有待理论与实验工作的进一步探索. 致谢:感谢潘程扬、刘雨霖同学的讨论交流.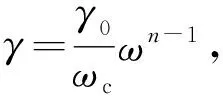
2 实验仪器
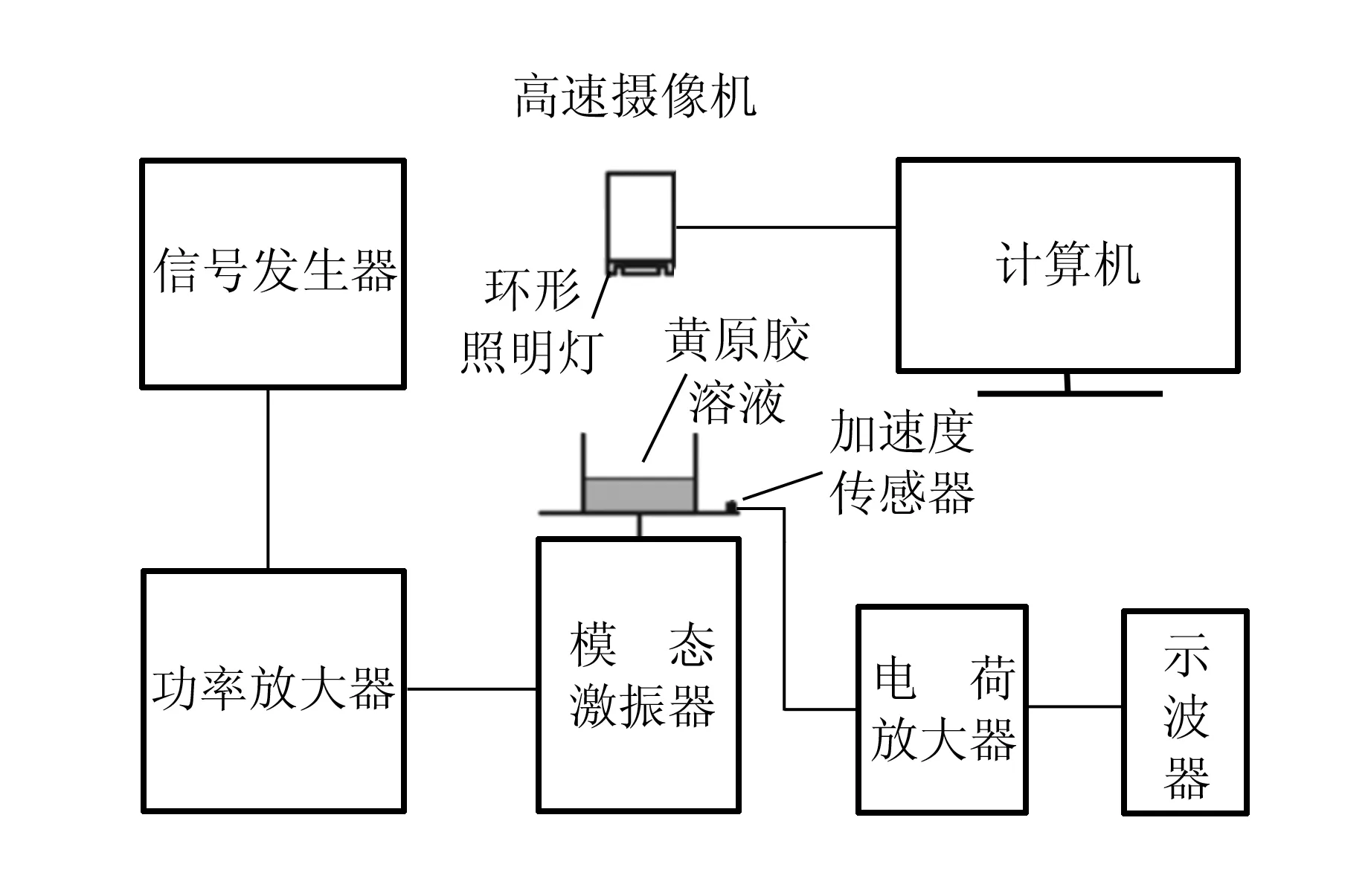
3 测量方案
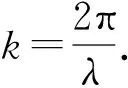
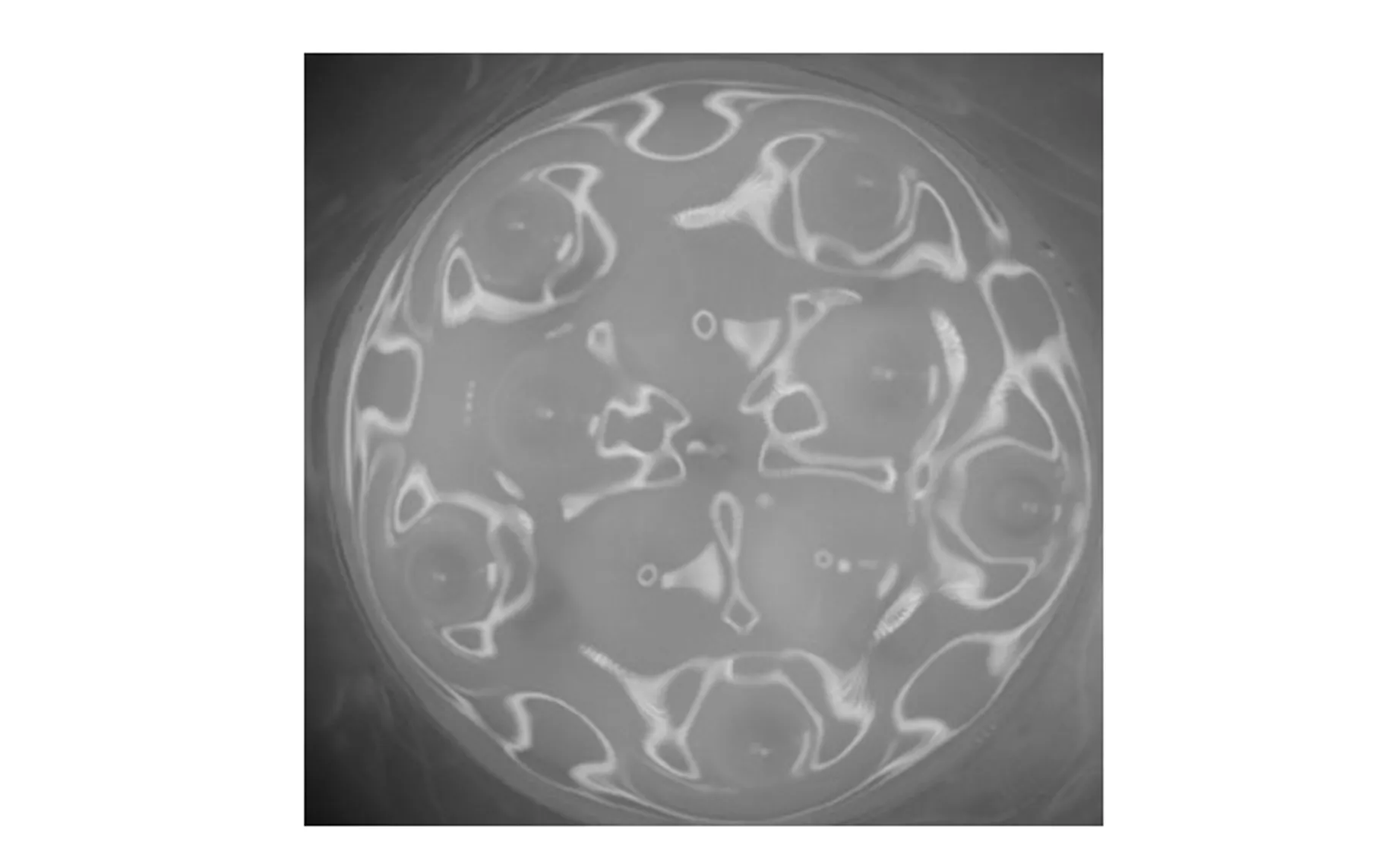

4 实验结果及分析

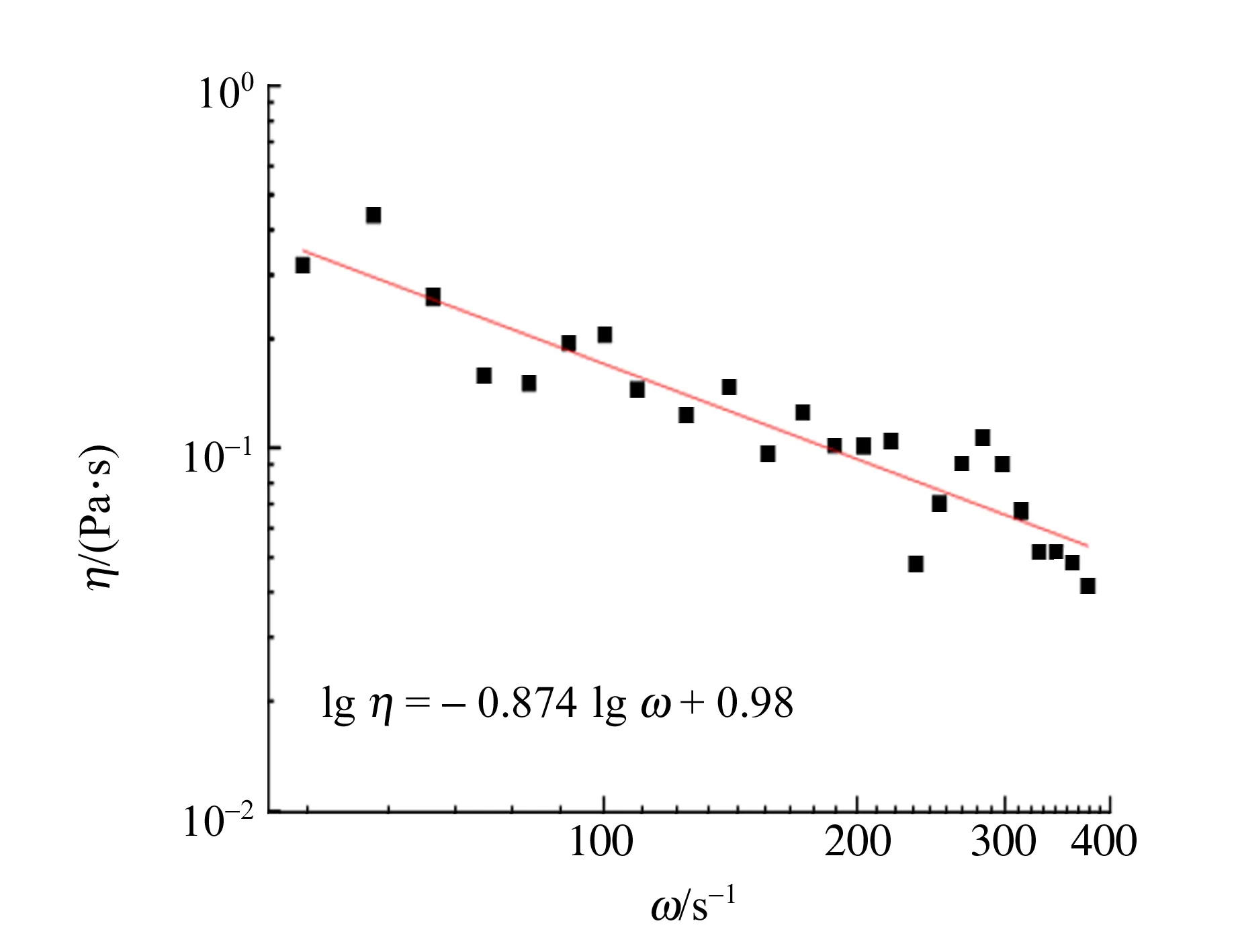
5 结 论

