地震荷载作用下超大跨扁平地下硐室位移特征的影响因素

陶连金， 张乃嘉， 安 韶

(北京工业大学 城市与工程安全减灾教育部重点实验室， 北京 100124)

0 引 言

21世纪以来，地下空间的开发利用越来越受到重视。随着我国经济、国防等事业的飞速发展，在水利、军事、交通、石油等工程建设中，越来越多的大跨度、大断面地下硐室工程不断涌现。如近几年集中建设的大型水电站地下厂房、国家战略石油地下水封岩洞储备库及核废料储存库等。硐室建设工程除了常规硐室外，还涌现出很多大跨及超大跨扁平硐室结构。目前，国内外地下硐室工程在跨度上也正逐渐朝着巨型跨度发展。而地震是给地下建筑带来严重破坏的主要灾害之一。如1906年美国旧金山地震[1]，1923年日本关东大地震[2]，1976年唐山大地震[3]，1995年日本阪神地震[4]，2008年汶川大地震[5]等都对地下工程造成了不同程度的破坏。一旦此类超大跨硐室在地震中遭到破坏，将有可能造成巨大的经济损失和人员伤亡，社会影响巨大。因此，研究超大跨度地下硐室的地震响应规律是十分必要的。

目前，无论是在震害调查还是数值分析方面，已经有学者做了大量的研究。S.Sharma 等[6]收集了世界范围内的 85 次地震中的 192 篇地下结构破坏实例报告，为地下结构的抗震研究提供了大量可靠的分析数据，并研究了地震动、硐室埋深、支护类型及岩石类型等对地下结构的影响。C.H.Doeding 等[7]整理分析了 71 座修建在岩体中隧道的震害资料，总结了岩体地下硐室在地震作用下的震害特点及规律，定性划分了岩体地下硐室的破坏程度，分析了地下硐室破坏程度与峰值地震动参数之间的关系，进而提出了地震作用下岩体地下硐室的地面峰值加速度破坏阈值。I.D.Moore等[8]推导了无限介质中双衬砌隧道在地震荷载作用下的三维响应计算公式，从理论和数值两方面证明了该方法的收敛性。Y.M.A.Hashash等[9]对地下结构抗震设计进行了总结与归纳。文献[10-15]应用有限元、有限差分，离散元等方法，分析了地下岩体硐室在地震动荷载作用下的加速度、位移、应力等响应特征和规律。文献[16-17]结合工程实例对超大跨度扁平地下硐室的开挖方式、稳定性等进行了研究。就目前研究来看，针对超大跨度扁平地下硐室的动力响应分析较少。因此，文中依托于国内某超大跨扁平地下硐室工程，采用动力时程分析方法，分析了在地震作用下，地应力特征、围岩条件、硐室跨度、地震荷载峰值对超大跨度扁平地下岩体硐室位移特征的影响，以期能为今后类似工程的抗震设计提供一些概念性指导。

1 计算模型与参数

1.1 工程背景

国内某超大跨扁平地下硐室工程区以厚-巨厚层的白云质灰岩、灰岩为主组成，自然状态下单轴抗压强度为95～125 MPa，岩体完整坚硬致密，强度高、抗风化能力强，围岩强度等级为Ⅱ级。硐室结构尺寸如图 1 所示。断面跨度 66.3 m，高 17.4 m，侧墙高度 4.4 m，矢跨比为 0.262，硐室埋深 120 m。采用喷射混凝土进行初期支护，强度等级为 C30，厚 0.25 m；二次衬砌强度等级为 C45，侧墙部位厚 1.4 m，拱顶部位厚 0.9 m，混凝土材料参数如表 1 所示。

图1 硐室及二衬支护Fig. 1 Cavern dimensions and supports

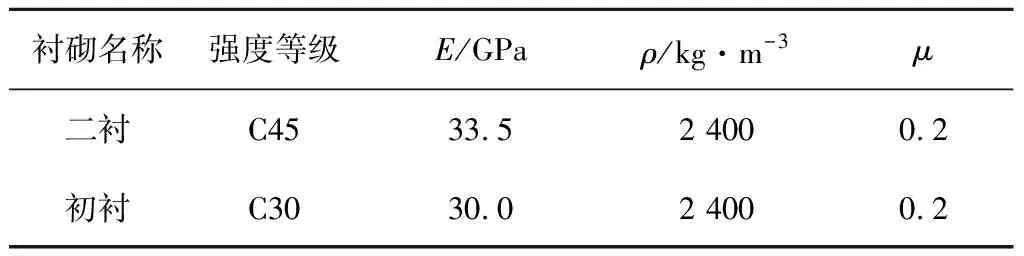
表1 混凝土材料参数

1.2 硐室-结构有限元模型

对超大跨扁平地下硐室进行横向地震响应分析，建立了围岩-结构有限元二维平面应变模型。GB 50909—2014《城市轨道交通结构抗震设计规范》[18]规定：“采用时程分析方法时，计算模型的侧面人工边界距地下结构距离不宜小于3倍地下结构水平有效宽度，底面人工边界宜取至设计地震作用基准面且距结构的距离不小于3倍地下结构竖向有效高度”。因此，确定模型尺寸长×高为500 m ×200 m，侧面人工边界距地下结构距离为3.27倍地下结构水平有效宽度，底面人工边界取至地震作用基准面且为3.6倍地下结构竖向有效高度，满足边界条件要求。

数值模型网格划分如图 2 所示，结构及围岩均采用CPE4R单元，共8 977个单元。初期支护与围岩之间采用绑定连接，初期支护与二次衬砌之间设置摩擦接触，摩擦因数设为0.4。网格划分在硐室开挖面及其附近加密，远离硐室开挖面处网格逐渐增大。模型网格最小尺寸为1 m×1 m，最大为4 m×4 m。基于廖振鹏[19]的分析结果，土单元网格尺寸需满足：

式中：hmax——土单元网格的最大尺寸；

vs——土层的剪切波速，依据实际地勘资料，取为1 549 m/s；

fmax——输入地震动的最大振动频率，模拟中选用Kobe地震波，最大振动频率为1.44 Hz。

经过计算，土单元最大尺寸为 6.72～14.34 m。由以上分析可知，网格尺寸满足计算要求。

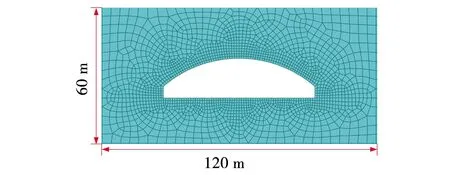
图2 硐室周边网格划分Fig. 2 Grid division around hole

地下硐室地震荷载作用下位移特征，以拱顶、底板中水平相对位移表示。监测点设置如图3所示。

图3 监测点设置Fig. 3 Setting of monitoring points

1.3 围岩模型与参数

数值分析中，结构采用线弹性模型，地下硐室岩体采用理想弹塑性模型，服从Mohr-Coulomb 屈服准则，屈服函数为

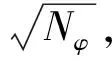
ft=σ3-σt,

式中：φ——内摩擦角；

σ1、σ3——最大、最小主应力；

c——黏聚力；

σt——抗拉强度。

当岩体内部某一点应力满足fs<0，发生剪切破坏;当岩体内部某一点应力满足fs>0，发生张拉破坏。文中依据实际工程情况，考虑了3种围岩条件，岩体力学参数如表 2 所示。其中Eo为变形模量。

表2 岩体力学参数

1.4 模型边界与分析步设置

模型计算分3步进行。首先在静力计算阶段，模型两侧水平向约束，底部边界双向固定。在重力作用下使模型区域的岩石介质材料达到地应力平衡；然后使用型号改变命令[20]在模型区域内开挖超大跨度扁平地下硐室，继续在重力作用下进行模型区域在开挖后的应力重分布直到完成，再进行初衬混凝土的喷射及二衬结构的施加。

完成静力部分模拟分析后，考虑到有限的计算模型区域边界可能造成波的反射，给数值分析结果的准确性造成一定影响，因此将静力边界撤除，最后在模型周围施加黏弹性动力边界。该边界将波动作用转换成人工边界节点作用力来实现地震动的模拟，降低了地震波反射对分析结果的影响[21-22]。

1.5 地震荷载与阻尼的确定

依据地震危险性报告，当地设防烈度为7度，对应的地震动加速度峰值为0.1g，考虑到地下建筑物的使用功能，进行提高一度设防，地震加速度峰值取0.2g进行数值分析。输入地震波选用日本阪神地震波。阪神波为近场地震波，频带相对较窄，主震频率范围主要分布在0.7～3.0 Hz，低频成分丰富，卓越频率为 1.45 Hz，分析时长为 30 s。地震波加速度峰值为 0.2g时的阪神地震波时程曲线及傅氏谱曲线如图4所示。动力计算中采用 Rayleigh 阻尼，即

C=αM+βK

，

式中:M——质量矩阵，

K——刚度矩阵，

α、β——常数，计算得出α=0.4，β=4×10-3。

图4 输入地震动时程曲线及傅里叶谱Fig. 4 Time history curve and Fourier spectrum of input seismic wave

2 硐室位移的影响因素分析

2.1 地应力特征

以最大水平地应力与垂直地应力的比值(侧压力系数)表征不同的地应力状态。垂直应力可近似表示为岩体自重(σv=γh)，最大水平主应力取为σh=λσv。我国实测资料表明,侧压力系数多为0.5～3.0[23]，文中分别取侧压力系数为0.5、1.0、1.5、2.0、2.5、3.0进行模拟计算，地震波加速度峰值取为0.2g。

地下硐室在地震荷载下的反应可以用硐室顶底的相对水平位移差来表示。图5为硐室顶底相对位移与侧压力系数的关系曲线。随着侧压力系数的增大，硐室在动力作用下顶底相对水平位移整体先减小而后趋于稳定。围岩级别为Ⅱ类时，6种侧压力系数条件下的相对位移s分别为10.3、9.6、9.5、9.4、9.4、9.6 mm，与侧压力系数λ为0.5工况相比，λ为1.0、1.5、2.0、2.5、3.0时的相对位移分别降低了6.8%、7.7%、8.7%、8.7%、6.8%。由以上分析可知，当λ由0.5(垂直应力主导)增长到1.0时，位移的量值和变化幅度较大，但当λ>1.0(水平应力为主导)时，侧压力系数对硐室顶底相对水平位移变化影响较小，位移曲线基本趋于稳定。当λ为3.0时，相对位移出现较小幅度的增长。

图5 硐室顶底相对位移与侧压力系数的关系Fig. 5 Relationship between relative displacement of surrounding rock top and bottom and lateral pressure coefficient

为探究侧压力系数λ为3.0时，相对位移出现增长的原因，提取地震作用后λ为0.5、1.0、3.0时围岩塑性应变云图,如图6所示。由图6可知，λ为3.0时验算点相对位移出现增加的趋势，是由于硐室拱顶出现了塑性区。在地震作用下，围岩拱顶处进入塑性状态，导致验算点相对位移增加。

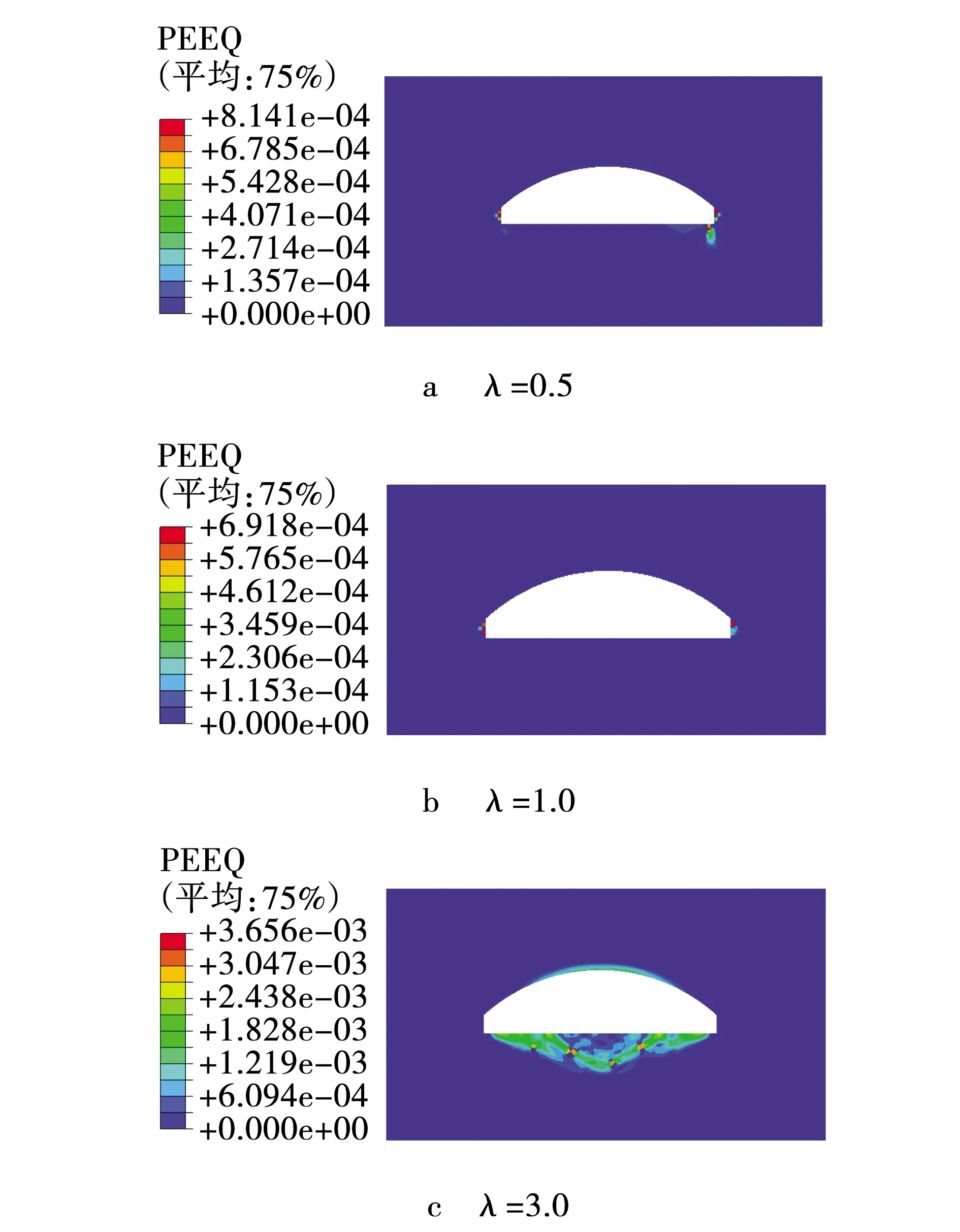
图6 地震动作用后围岩塑性区云图Fig. 6 Contour of surrounding rock plastic zone after earthquake

2.2 围岩类别

图7为硐室顶底相对水平位移随围岩级别的变化曲线。由图7可知，在地震作用下，围岩级别对硐室顶底相对位移有着显著影响，不同侧压力系数条件下硐室位移特征规律一致，即围岩级别越高，硐室顶底相对位移越小。当侧压力系数λ为0.5时，与围岩级别Ⅲ2工况相比，围岩Ⅲ1与Ⅱ工况相对位移分别降低了6.25%、15.97%；当侧压力系数λ为1.0时，与围岩级别Ⅲ2工况相比，围岩Ⅲ1与Ⅱ工况相对位移分别降低了8.04%、24.47%；当侧压力系数λ为3.0时，与围岩级别Ⅲ2工况相比，围岩Ⅲ1与Ⅱ工况相对位移分别降低了8.22%、23.69%。由此可知，随着围岩级别的增加，相对位移呈现非线性的降低趋势，地下硐室抗震性能明显提高。

图7 硐室顶底相对位移与围岩条件的关系Fig. 7 Relationship between relative displacement of roof and bottom of cavern and surrounding rock conditions

2.3 跨度

保持硐室矢跨比及埋深不变，调整硐室跨度b为30.0、40.0、50.0、66.3 m，对比分析不同跨度硐室的地震反应位移响应。图8为围岩条件为II类，输入地震动峰值为0.2g时，硐室顶底相对水平位移随硐室跨度的变化曲线。随着硐室跨度的增大，硐室顶底相对位移差逐渐增长。当跨度为30 m时，不同侧压力系数下硐室拱顶底相对位移基本相等，说明当结构硐室跨度较小时，地震对不同侧压力系数的硐室位移特征影响并不显著。当硐室跨度达到或超过50 m，侧压力系数为0.5时，拱顶底相对位移明显大于λ≥1.0时的工况。这是因为随着硐室跨度的增加，以竖向应力为主导(λ<1.0)的地下硐室在水平地震作用下响应愈来愈剧烈，从而导致围岩顶底相对位移明显增加。随着硐室跨度的增加，不同侧压力系数硐室地震位移特征差异性越大。对超大跨扁平地下硐室来说，其跨度越大，硐室顶底相对水平变形越大，在地震中稳定性越难保证，抗震设计中尤其需加强支护。

图8 硐室顶底相对位移与硐室跨度的关系Fig. 8 Relationship between relative displacement of roof and bottom of cavern and cavern span

2.4 地震波加速度峰值

将地震波加速度峰值依次调整为 0.1g、0.2g、0.3g、0.4g，以探究加速度峰值对硐室位移响应的影响。图9为围岩级别为II类时，侧压力系数分别为0.5～3.0的硐室顶底相对水平位移随地震峰值变化的曲线。图中横坐标为输入的地震动加速度时程的峰值，以重力加速度g的倍数表示，纵坐标为硐室顶底相对位移。

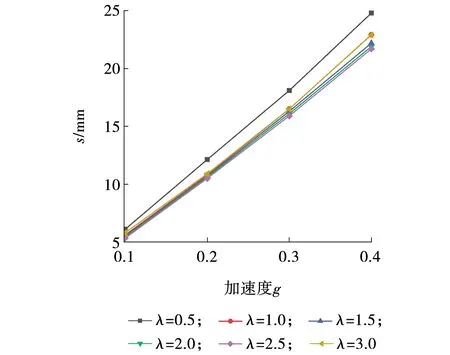
图9 硐室顶底相对位移与地震动峰值的关系Fig. 9 Relationship between relative displacement of surrounding rock top and bottom and peak ground acceleration

由图 9 可见，随着地震波加速度峰值的增大，硐室顶底相对位移基本呈线性增长，强震作用对硐室稳定影响明显。λ=0.5时的顶底相对位移大于λ≥1.0时的顶底相对位移，说明当λ<1.0，即垂直应力为主导时，不利于硐室在地震作用下的稳定。

3 结 论

(1)在地震荷载作用下，硐室相对位移随侧压力系数增大先减小后趋于稳定。当λ从以垂直应力为主导(λ<1.0)转换为水平应力为主导(λ>1.0)时，位移减小幅度较大。由垂直应力为主导的硐室顶底相对水平反应位移明显大于由水平应力为主导的情况。围岩级别对地震作用下的硐室顶底相对位移影响显著，围岩级别越高，整体性越强，抗震性能越好。

(2)对超大跨扁平硐室，跨度是影响硐室地震反应位移特征的重要因素。随着硐室跨度的增大，硐室顶底相对水平位移逐渐增长。硐室跨度越大，不同地应力特征对硐室顶底相对水平位移影响差异越大，其在地震作用下的稳定性越低，应加强支护。

(3)地震动峰值对硐室顶底相对水平反应位移的影响显著。随着地震动峰值的增大，硐室顶底相对位移呈线性增长。与水平应力为主导的工况相比，以垂直应力为主导的硐室在地震作用下的抗震稳定性更不利。