江苏省城市物流发展水平实证分析

沙如雪

(南京财经大学，江苏 南京 210023)

一、引言

物流业是支撑国民经济发展的基础性、战略性和先导性产业，与人们的日常生活息息相关。党的十八大以来，在习近平总书记关于现代物流业重要论述的指导下，我国现代物流业发展质量明显提高，公路、铁路、水运等货运量以及快递业务量的发展速度均跃居全球前列，物流政策环境不断优化，物流业不断发展壮大。

物流业的高质量发展可以促进一系列相关产业的发展。因此，物流业的发展水平已成为衡量一个国家实力和现代化水平的重要指标之一。经过几十年的努力，自2013年以来，中国已成为物流业发展大国，拥有世界顶级的物流市场。

物流业的稳定高效发展与促进区域经济发展密切相关。江苏省地处中国东部沿海地区、长江经济带，经济发展综合水平一直走在全国前列，全省整体经济特征为“南强北弱”。2019年10月，江苏成为全国首批交通电力试点地区之一。在这种背景下，研究江苏省区域物流发展水平，全面认识江苏省物流业发展差异，有利于促进江苏省城市物流业健康可持续发展，提高江苏省整体经济发展水平。

目前中国学者对物流业的发展进行了一系列的研究。刘洪芹运用GEM模型选取指标，分析河南省各城市物流发展水平状况，并提出相应建议。孙国钊从物流竞争力的角度构建了长江经济带城市物流竞争力评价体系。胡毅标准化全国数据、综合熵权法和模糊物元模型评价中部地区物流发展。郭鑫、徐君运用密切值法对长江经济带物流发展水平进行了综合评价。王明严、李芸嘉系统地回顾了区域物流竞争力的研究方法、范围和对象，并对未来物流发展水平的研究方向进行了展望。因素分析和聚类分析在物流综合分析中应用并不广泛。鉴于此，本文采用因子分析法对关联度高的指标进行分析，并对江苏省13个市的物流发展水平进行评价。同时，通过聚类分析，根据地级市物流发展水平的不同对城市进行聚类。

二、评价指标体系的构建

(一)评价指标体系设计原则

为构造出一套有关物流业发展水平的科学合理且可行性较强的评价指标体系，现根据如下三个原则选取本文所需的指标。

1.科学性

指标体系的选取要有代表性，科学合理，能够全面地反映江苏省各市的发展水平和综合实力，并且可以进一步找出各城市之间的差异性。

2.系统性

各指标之间要有必然的逻辑关系，它们不仅要从差异的侧面反映出物流业的竞争上风和薄弱环节，并且还要反映各部分之间的内在联系。

3.可行性

在选择指标时，应强调整体的可行性。指标选择的计量尺度和计算方法必须统一，必须选择概念清晰、数据容易获取、计算方便的指标。数据来源应真实可靠，避免出现不合逻辑、不准确且无效的数据。

(二)评价指标体系

本文在参考大量关于城市物流发展水平评价指标体系的文献并全面考虑数据来源、研究层次以及全面性的前提下，结合江苏省各市物流业发展水平的研究现状，构造了包括两级指标的物流发展水平评价指标体系，如表1所示。

表1 物流发展水平评价体系

(三)相关指标说明

1.经济发展水平

物流作为一种衍生需求，是经济的重要组成部分，在经济发展中发挥着重要作用。城市经济发展水平的高低间接决定了城市物流的发展水平。经济发展水平越高，对货物运输、包装、仓储、配送和加工物流服务的需求就越大。因此，物流的发展与经济的发展是正相关的。本文从区域生产总值、人均生产总值、区域常住人口数和城市常住居民人均可支配收入四个指标对城市经济发展水平进行评价。

2.物流产业规模

影响物流规模的因素很多，其中物流需求是主导因素。本文通过查阅大量文献，选择用社会消费品零售总额、进出口总额和邮政业务总额这三个指标来衡量物流业的规模。

3.物流发展基础

城市物流业的发展离不开城市良好的基础设施。本文以公路货运量、公路里程为计量指标，通过城市基础设施的发展规模来反映区域物流的发展潜力。

4.信息化程度

物流业的飞速发展，离不开现代通信技术的广泛使用。较高的物流效率不仅能为企业节省运营成本，还能带来优质的服务体验。一个地区的信息化水平在一定程度上决定了现代物流业发展的前景，本文以互联网宽带接入用户和年末移动电话用户作为衡量指标，来反映一个地区的信息化水平。

三、物流发展水平的定量评价

(一)原始数据收集

本文的数据主要来源于«2020年江苏统计年鉴»，选取了2019年江苏省城市物流业发展水平相关指标数据进行综合评价分析。共选取了11个指标数据，且均为正指标。

(二)研究方法

关于物流发展水平的评价方法有很多种，本文根据研究对象和研究实际情况采用因子分析和聚类分析。

因子分析(factor analysis):利用降维思想，用几个不相关的综合变量来表示多个关系复杂的原始变量，这些综合变量可以尽可能多地包含原始变量的信息。因子分析模型为:设有

n

个相关性较强的可观测随机变量，即

X

，

X

，…，

X

，现从中提取公共因子

F

，

F

，…，

F

(

m

≤

n

)，则模型的矩阵形式为:

X

＝

AF

＋

ε

。即:

其中，公共因子

F

，

F

，…，

F

相互独立且不可测，

ε

，

ε

，…，

ε

为特殊因子，相互独立，且与公共因子的协方差为零。

聚类分析(cluster analysis):将相似度较大的聚类归为一类，将另一些相似度较大的聚类归为另一类，以此类推，最终形成完整的分类体系。最后再用一个树状图来表示所有样品间的亲近程度。

(三)实证分析

1.因子分析

(1)原始数据处理与检验。本文主要使用的统计软件为SPSS，对表1中的11个指标数据进行因子分析。由于数据中缺失值较少，故采用均值替代法进行处理。由于数据之间的差距很大，为了减少数据差异，并消除数据差异造成的影响，应该对数据进行标准化处理，使因子分析的结果更加准确。公式如下:

其次，在进行因子分析前，需要对原始数据进行KMO和Bartlett球形检验，判断其是否适合做因子分析。

从表2中数据可看出，KMO的值为0.722>0.6，适合进行因子分析。此外，Bartlett球形检验值为262.760，对应的概率接近0.000<0.05，拒绝原假设H0，表明原始变量之间相关性较强。因此，该数据可以进行因子分析。

表2 KMO和Bartlett的检验结果

(2)公共因子的提取。本文采用主成分分析法提取主因子，从原始数据的相关矩阵中得到矩阵的特征值和特征向量。根据初始特征值大于1、累积方差贡献率大于85%的原则，从矩阵中提取公因子，如表3所示。

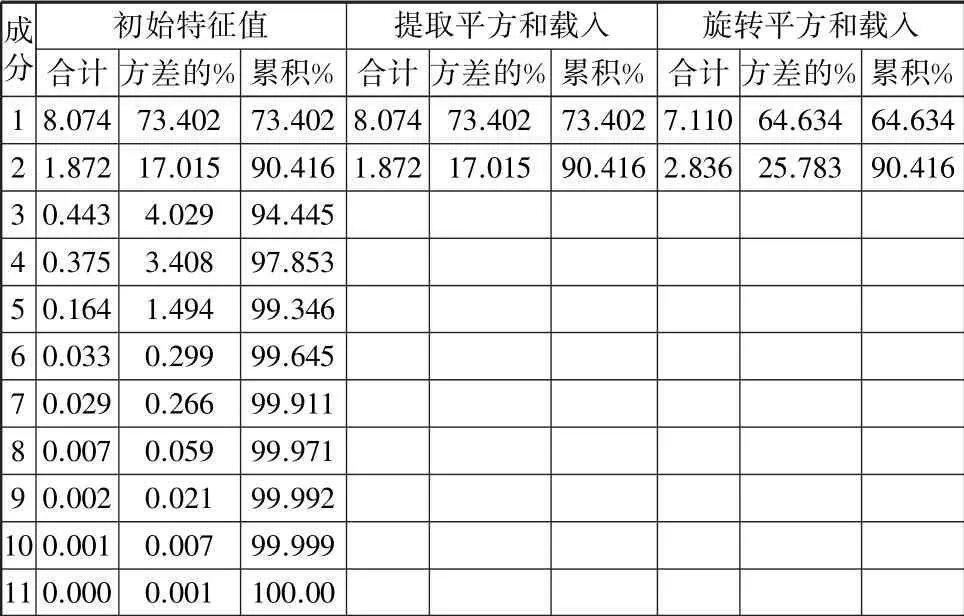
表3 解释的总方差

从表3的数据可以看出，本文提取了两个公因子，分别记为

F

，

F

，提取的公因数旋转后的累积方差贡献率达到90.416%，基本代表了原变量的大部分信息，可以作为评价和分析城市物流发展水平的主因子。

此外，为使分析更加清晰直观，可由因子的特征值及因子的数量关系画出相应的碎石图。从图1的碎石图中可以看出，前两个因子对应的曲线较为陡峭，而从第三个因子开始对应的曲线趋于平缓。此外，碎石图表明，前两个因子的特征值都大于1。因此，选择前两个公共因子作为本研究的主因子较为合适。

图1 碎石图

(3)旋转前后的因子载荷矩阵。通过对提取的公共因子进行分析，得出成分矩阵，也就是因子载荷矩阵。为了使因子分析法求出的因子载荷矩阵简化，便于对主成分进行专业上的解释，需要进行因子旋转。本文采用方差最大法对因子载荷矩阵进行正交旋转，使各公共因子的方差差异性达到最大。由此得到旋转后的因子载荷矩阵，即旋转后的成分矩阵，如表4所示。

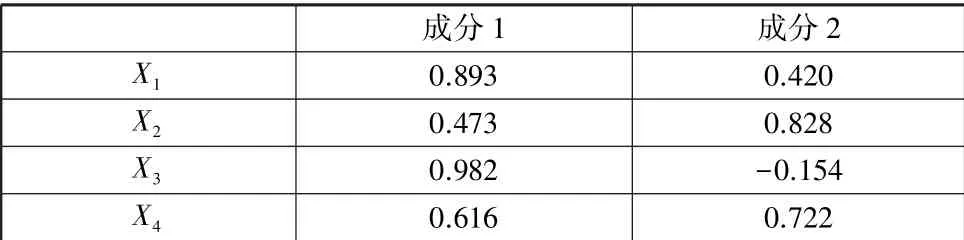
表4 旋转后的成分矩阵

续表

由表4中数据可以看出，虽然公共因子解释数据的能力没有发生变化，但是，旋转后的因子载荷矩阵发生了变化，各指标在公共因子上的载荷量更加接近于0或者正负1。

(4)各因子得分函数。运用回归法根据四个公共因子求得因子得分系数矩阵，如表5所示。

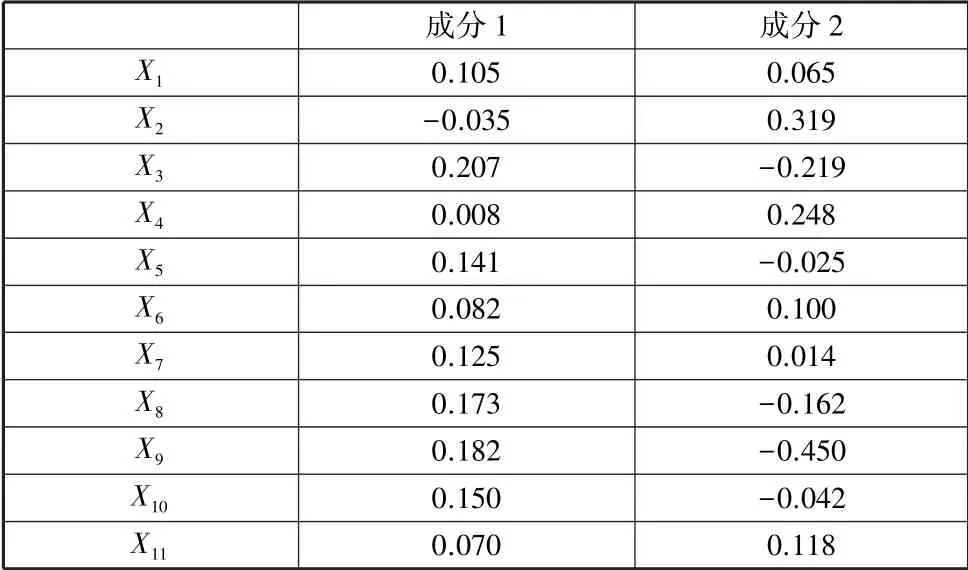
表5 成分得分系数矩阵

由于原始数据经过标准化，所以根据标准化数据求出的因子得分系数只是一个相对数，数据有正有负，在正负1之间，数据为正表明该因子得分超过平均水平，数据为负表明低于平均水平。

(5)因子得分与排名。在因子得分系数矩阵的基础上，运用回归法求得各因子得分函数:

F

＝0

.

105

X

－0

.

035

X

＋0

.

207

X

＋0

.

008

X

＋0

.

141

X

＋0

.

082

X

＋0

.

125

X

＋0

.

173

X

＋0

.

182

X

＋0

.

15

X

＋0

.

07

X

F

＝0

.

065

X

＋0

.

319

X

－0

.

219

X

＋0

.

248

X

－0

.

025

X

＋0

.

1

X

＋0

.

014

X

－0

.

162

X

－0

.

45

X

－0

.

042

X

＋0

.

118

X

在因子得分函数的基础上，以各因子的方差贡献率占个因子总方差贡献率的比重作为权重进行加权汇总，得出各地区的综合得分

F

，即:

F

＝(64

.

634×

F

＋25

.

783×

F

)

/

90

.

416对表5中数据进行处理计算得主因子得分

F

、

F

及综合得分

F

，并根据得分对变量进行排序，得到江苏省13个市物流发展水平的因子得分及综合排名表(表6)。

表6 江苏省13个市物流发展水平的因子得分与排名

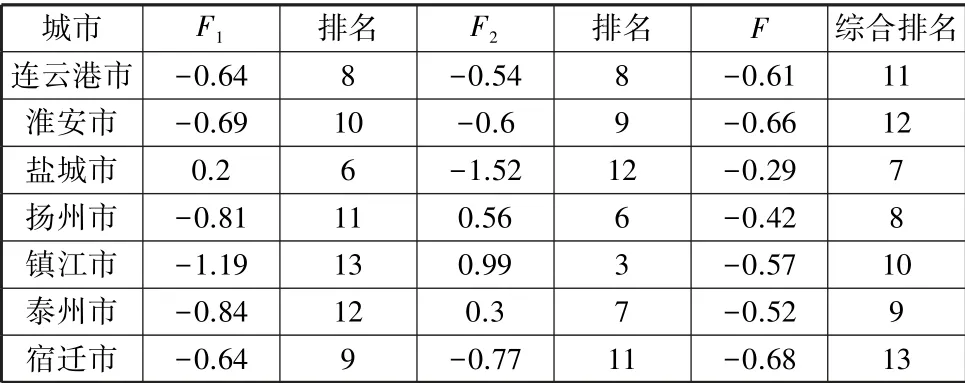
续表

从表6中的因子得分和排名可以看到，在第一公共因子上得分较高的为苏州、南京、徐州、南通等，主要是经济较发达的城市，这些城市交通便利、人口众多，表明该区域有巨大的物流需求和良好的物流基础设施；在第二个公共因子上，无锡、常州、南京、镇江等城市得分较高，主要集中在苏南地区，表明该区域的人均经济发展水平高，消费能力较强，物流发展潜力大；苏州、南京、无锡、徐州等城市的综合因子得分排名靠前，表明这些城市的物流业综合实力较强。

(6)因子分析结果。为了使分析更加直观清晰，将2019年江苏省13个市的物流发展水平的因子得分及综合排名表(表6)转为柱形图，如图2所示。

图2 2019年江苏省13市因子得分柱状图

从图2可以看出，整体上可以将因子分成两类，即大于0的和小于0的，其综合得分大于0的城市代表物流业发展状况良好，而小于0的城市相对来说还有薄弱环节，需要进一步改进。总的来说，2019年苏州、南京、无锡、徐州等地的物流发展水平综合得分大于0，高于全省平均得分，而宿迁、淮安、连云港、镇江等地的物流发展水平综合得分小于0，低于全省平均得分。

具体来说，从全省综合得分排名来看，苏州、南京、无锡2019年物流发展水平综合得分远高于其他城市，处于全省中上等水平；徐州、南通、常州相对于苏州、南京这些城市，物流发展水平综合得分有一定的差距，但是仍然处于全省中等水平；而剩余城市如宿迁、连云港等地区在综合得分上大多小于0，低于全省均分，处于全省中下等水平。

目前，从以上的排名得分来看，城市物流发展水平与地理位置、地区经济发展水平有一定的联系。一般来说，地理位置优越的地区有一定的经济发展优势，综合实力较强，相应地，物流业的发展也不落后。

2.聚类分析

根据表6得到的综合得分，对江苏省13个市进行聚类分析，其中度量标准采用平方欧氏距离，类别间距离采用组间联接法，得到聚类分析的树状图，如图3所示。

图3 聚类分析树状图

根据图3聚类分析得出的结果，本文将13个城市的物流发展水平分为三类，结果如表7所示。

表7 聚类分析结果

第一类是物流发展水平较高的城市，即苏州和南京。2019年，苏州物流发展水平综合得分为1.8，南京物流发展水平综合得分为1.2，分别位居江苏省第一、第二位。苏州和南京都是经济发展规模大、工业基础强、贸易流通繁荣的城市。这些条件支持了物流业的强劲发展，为未来物流竞争提供了强大的潜力。

第二类是物流发展水平较高的城市。从表7可以看出，江苏省物流发展水平较高的城市有无锡、徐州、南通、常州，其综合得分均超过0，在全省排名较为靠前。这些城市处于江苏省中上游的经济发展规模和物流供给能力，反映了这些城市经济实力强、物流需求大、信息化水平高，物流基础设施建设相对完善，物流业未来的发展潜力不可低估。

第三类是具有一般物流发展水平的城市，即淮安、宿迁、连云港、镇江、泰州、盐城、扬州等城市。这些城市的综合得分为负，说明这些城市的物流发展水平低于江苏省物流业发展的平均水平。

四、结论及建议

(一)结论

本文通过构建物流发展水平评价体系研究了2019年江苏省内13个城市的物流发展水平的高低关系，通过因子分析得出苏州、南京、无锡的物流发展水平综合得分远远高于其他城市，处于全省中上等水平；徐州、南通、常州相对于苏州、南京这些城市，其物流发展水平综合得分有一定的差距，但是仍然处于全省中等水平；而剩余城市如宿迁、连云港等地区在综合得分上大多小于零，低于全省均分，处于全省中下等水平。

接着利用因子分析的得分情况进行聚类分析，分析得出可以将13个城市的物流发展水平分为三类，第一类为物流发展水平高的城市，即苏州、南京，第二类为物流发展水平较高的城市，有无锡、徐州、南通、常州，第三类为物流发展水平一般的城市，为淮安、宿迁、连云港、镇江、泰州、盐城、扬州等城市。

从因子分析和聚类分析研究的结果来看，物流发展水平与地理位置及地区经济发展水平有一定的联系，江苏省内物流发展水平呈现较为明显的地区差异，苏南地区城市经济发展水平较高，基础设施完善，物流业规模大，信息化程度高，发展水平较高。一般来说，地理位置优越的地区有一定的经济发展优势，综合实力较强，相应地，物流业的发展也不落后。

(二)建议

现代物流业是支撑国民经济发展的基础性行业，也是引导产业布局创新的先导性产业。通过区域协同、韧性联动，加强物流业在地区间的联系，使得各地区的物流业发展逐渐趋向均衡发展。江苏省内物流发展水平较高的地区如苏州和南京，可以通过加强区域物流合作来解决地区间发展的不均衡问题。构建“通道＋枢纽＋网络”的现代物流体系，以适应复杂多变的经贸环境，把握经济高质量发展的时代要求。值得注意的是，物流业的发展离不开新平台、新技术、新理念的融合，在加强区域协同发展的同时要注重加强物流业的创新。同时，在物流业发展态势逐渐良好的情况下，也要更加注重绿色健康的发展，加强科技创新、加强智能研发的同时减少能耗，提升企业效率，夯实科学完备的现代物流基础体系。