值得修炼的教师“诊评”功夫——从一次课堂记录说起

☉江苏省泰州市姜堰区实验初级中学 鲍爱珍

数学教师需要修炼很多专业基本功，如南京大学哲学系郑毓信教授指出的“善于提问”“善于举例”“善于比较和优化”，这三项基本功引发很多教研专家的共鸣。近年来，《中学数学》（初中版）上有多篇文章提到“三项基本功”.此外，结合教师在课堂中的主导作用，笔者认为，教师在课堂上面对课堂生成，非常需要修炼“诊评”功夫.本文就从一次听课记录说起，记叙听课观感及对教师“诊评”功夫的一些初步思考.

1 从一次听课记录说起

最近观摩一节公开课教学，课题是一元二次方程单元教学起始课，执教者是一名青年教师Z.近年来，很多地区积极推行“单元教学”，鼓励教师整合教材内容，让学生整体研究某个数学单元，如一元二次方程的单元教学起始课，着重引出一元二次方程的概念与相关概念，并初步探索一元二次方程的不同解法，让学感知一元二次方程部分即将学习的主要内容.青年教师Z由一个实际问题引出新知，定义一元二次方程之后，安排学生分别研究两个一元二次方程（x2-4＝0，x2＋6x-16＝0）的解法，以下是师生对两个方程的解法的教学记录：

生1：可以将x2-4＝0移项，得x2＝4，直接开方，得x＝2或x=-2.

师：正确！你通过移项，利用直接开方法求出方程的解，还有其他解法吗？

生2：我是将方程x2-4＝0左边进行变形，得（x＋2）（x-2）＝0，然后可得x＋2＝0或x-2＝0，也可求得x＝2或x=-2.

师：你这样做的依据是什么？

生2：左边是因式分解，然后根据乘法的性质：两个数的积为0，则这两个数中必有一个因数为0.

师：很好！你运用因式分解，将二次方程转化为两个一次方程，同样实现了降次，求出方程的解.两个解可以表示为x1＝2，x2＝-2.请大家继续思考如何解方程x2＋6x-16＝0.

学生陷入思考，两分钟后，陆续有学生示意已有解答，教师安排学生上台展示.

生3：我是将方程x2＋6x-16＝0左边因式分解，得（x＋8）（x-2）＝0，解得x1＝2，x2＝-8.

师：正确.还有不同的解法吗？

生4：我是这样解的，两边同时加上25，得x2＋6x-16＋25＝0＋25，化简得x2＋6x＋9＝25，这时左边是一个完全平方式，可以写成（x＋3）2＝25，然后直接开方，得x＋3＝5或x＋3＝-5，于是x1＝2，x2＝-8.

师：很好！说说你是怎么想到这种思路的.

生4：我是想凑出一个完全平方式x2＋6x＋9，所以要对左边的x2＋6x-16加上25，才能写成（x＋3）2，根据等式的性质，方程的右边也要加上25，所以可得出（x＋3）2＝25.

师：大家听懂了吗？（众生表示理解）很好！你帮这种解法取一个名字吧！

生4：配方法.

师：好！就叫配方法.

听课简评：以上关于一元二次方程解法探究的教学过程中，学生思维灵活，教师追问得当，顺利引出一元二次方程的不同解法，让学生自主发现了一元二次方程的不同解法（直接开方法与因式分解法），并且初步涉及配方法，知道一元二次方程的解决关键是“降次”.

教学记录：在本课小结之后，教师布置了一道作业题，用配方法求一元二次方程ax2＋bx＋c＝0（a≠0）的解.

听课随感：在课堂进程中，对于学生的这步变形“x2＋6x-16＋25＝0＋25”，教师如果没有及时优化表达，本课的作业中布置用配方法解一元二次方程ax2＋bx＋c＝0（a≠0），就显得要求偏高（本质上是运用配方法推导一元二次方程的求根公式）.笔者认为，如果在学生的变形基础上，教师进一步做出如下“优化”（我们将采用虚拟师生对话的方式，给出教学优化），将有利于学生课后独立探究一元二次方程的求根公式.

生4：我是凑出一个完全平方式x2＋6x＋9，写成（x＋3）2，方程的右边也要加上25，所以可得出（x＋3）2＝25.

师：你讲得很好！根据你的想法，我将你写的过程重新书写一下（教师板书示范），看是否符合你的意图.

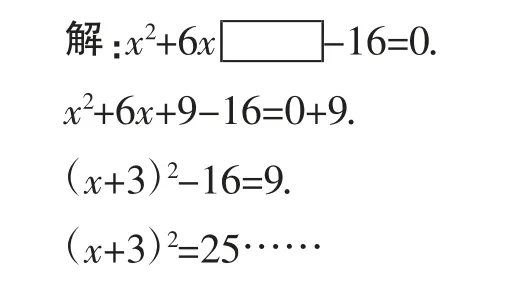
还可以换一种书写的“序”，

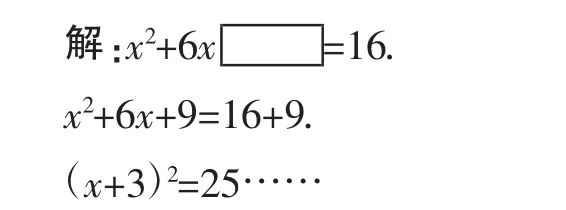
说明：我们可将上述书写方式称为“留白式”书写，这种书写方式，有利于后续学生研究更为复杂的配方法解一元二次方程，包括解题过程中“序”的意识也得到很好的渗透.

2 关于教师的“诊评”功夫的一些思考

2.1 教师对教学内容要有深刻理解

教师备课是很大的一个话题，其中深刻理解教学内容是最关键的.正如中国教育学会中学数学教学专业委员会理事长章建跃博士所指出的，很多教学乱象、教学不足，多是由于教师对教学内容的理解不深，即在“理解数学”上出现了偏差.以上文提到的一元二次方程的单元起始课为例，虽然几种不同的解法在本课只是初步涉及，只要学生能够顺利解出一些特殊形式的一元二次方程就达到了本课的教学目标，然而从有利于学生后续的“可持续发展”来看，如果学生在配方法的解法步骤上没有得到优化和规范，则不利于后续系列研究配方法解一元二次方程.可见，在这些教学细节上，如果教师课前对本课的教学内容没有达到深刻理解，在课堂教学中，就缺少“预案”，也就难以做出必要的纠正或优化.从这个意义上看，深刻理解教学内容，不只是关注本课的教学内容和目标达成，还要关注本课的教学内容或一些教学细节对学生后续学习有怎样的示范和引领价值，教师的高观点、教学设计的高立意往往能在这些教学细节、教学诊评中得到体现.

2.2 教师在课堂教学中要重视倾听

华东师范大学李政涛教授关于教师的“倾听”功夫有很多深刻的见解，值得我们学习，并在教学中加强课堂倾听功夫的修炼.具体来说，在精心设计的问题驱动下，学生经历独立思考后，有些问题需要适当安排学生进行小组讨论与交流，教师可参与小组的讨论，倾听学生的观点，捕捉一些有价值的观点，然后安排全班交流互动；或者学生在上台讲题或展示时，教师要注重倾听，根据教学需要进行追问或点评，对于一些有价值的学生观点，可以让台下的学生再次复述，并追问“你们是如何理解他的观点（或见解，或思路）的”.教师在倾听之后，以“促动师”的身份组织更多学生参与课堂活动，使得一两个学生的讲解变成全班的倾听与对话互动，让全班学生的思维被充分卷入课堂对话中.在这里还需要指出一种现象，那就是有些教师容易机械地“执行教案”，忽略学生课堂对话中一些精彩观点，而只挑战适合自己课前在教案中预设好的思路，对学生的一些精彩表达因为倾听不充分、不到位，使得一些有价值的观点或思路被忽略，这是一种教学遗憾.

2.3 教师针对课堂生成要精准诊评

我们在著名特级教师李庾南的课堂教学中，常常很享受李老师课堂倾听、诊评的教学功夫，背后是李老师长达六十多年的课堂教学经历.课堂教学中，处理好预设和生成是关键，然而“知易行难”，面对学生的生成，很多情况下，需要教师的“即兴”诊评功夫，而且诊评是否恰当、精准往往影响着教学品质.像上面学生关于配方法的解法步骤，如果教师“高度”肯定，当然对这个学生是很大的鼓励，然而，对其余没有想到这种“配方”技巧的学生却不会有很大的启发，如果能精准诊评，进行必要的优化表达，则可促进更多的学生掌握这类问题的“配方通法”，并且通过“留白式”书写，既化解了配方的难点，又有利于后续研究更多一元二次方程的配方法.当然，精准诊评作为一项专业基本功，是需要长期修炼的，也需要多观摩专家型教师的课堂（或录像），并从这些课堂教学中感悟出专家教师是怎样捕捉课堂生成的，又是如何精准点评这些课堂生成的，长期坚持下去，可发展教师的“学习力”，相信会有越来越多的青年教师能修炼出较好的课堂诊评功夫.