基于“情境—活动”的“有理数的加法”教学设计

☉江苏省扬州市邗江区公道初级中学 韦文进

针对初中阶段的数学教学，新课标给出了明确的教学要求，应当在课堂教学的过程中落实有效的学生活动，彻底改变学生被动听讲的教学格局，提高学生的参与度，使学生可以深入所学内容，展开主观、高效的数学学习，这一点也同样体现于核心概念教学实践.基于这样的观点，在初中数学教学中，采取“情境—活动”式教学，能够有效地促进学生数学学习的高效化.以下我结合“有理数的加法”这一教学实例展开简单剖析，谈谈基于“情境—活动”进行的教学设计.

1 创设问题情境，引入学习内容

情境1：小刚沿着某路向东行进a米，然后继续向东行进b米，请问：两次一共行进多少米？

学生活动：通过已知条件就能够准确辨析：根据已知条件，a、b都应当为有理数；根据问题能够了解这是两个有理数的相加，这样便能够顺势引入本课的课题.

2 引导自主探究，归纳加法法则

情境2：根据情境1的分析，请大家认真思考，梳理出a、b两数在符号上存在哪些可能.

学生活动：根据已有认知进行总结：同为正数、同为负数、一正一负、加数中至少有一个为0.

教师活动：当学生完成分类之后，还需要结合正确的引导，使学生立足于不同的情境，对有理数的加法法则展开深入讨论.在提出问题之后，应当给予学生相应的提醒，引导学生注意已知条件的真实含义.为了帮助学生理解，可以利用多媒体，通过建立数轴的方式为学生提供形象认知，在这一数轴中，取向东为正方向.

情境3：如果将a、b设为两种不同类型的有理数，在进行加法运算的过程中，你认为能够得出哪些结论？是否能够从中推导出有理数的加法运算法则？

学生活动：建立合作小组，以组为单位展开自主探究，梳理讨论具体的处理方法，预设可能呈现的结果.

预设1：同为正数.为a、b赋以任意值，例如，a=20，b=15，然后将对应过程呈现于数轴上.根据数轴可以发现a、b之和为35，写成算式为（+20）+（+15）=+35.

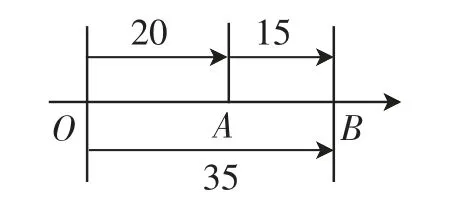
图1

对这一过程而言，教师应当预设其中可能存在的问题.例如，很多学生会认为这是一个非常简单的运算过程，即使不用数轴也不会出现计算错误.此时，教师应当给予相应的提醒，使学生了解使用数轴的根本目的并非是使计算过程更简单，而是呈现分析过程.还要告知学生，在未来的学习过程中，当涉及其他类似的知识或者问题时，也可以利用数轴，一方面，可以简化已知条件；另一方面，可以快速找到有效的解题思路.

预设2：同为负数.假设a=-20，b=-15，利用数轴呈现a、b两数并揭示对应过程，如图2.可以将这一过程转化为具体的场景：在这两个阶段，小刚都是向西行进，第1次行进20 米，第2次行进15 米，最终行进的距离为-35 米，由此得出算式：（-20）+（-15）=-35.

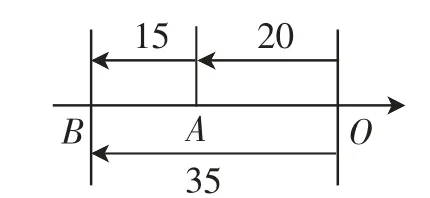
图2

预设3：一正、一负.假设a=+20，b=-15，将具体的对应过程呈现于数轴上，如图3所示.针对这一过程，可以理解为以下情形：在这两个阶段，小刚呈现出了两次不同方向的行进，第1次向东，第2次向西，确定最终的行进距离为+5 米.由此得出算式：（+20）+（-15）=+5.

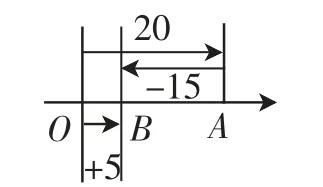
图3

预设4：对情形3中b的值进行修改，假设其为-25，具体的意义又该如何？如何利用数值对其进行处理？如何理解这一过程？结合数轴对应的过程可以发现，在这两个阶段，小刚分别向东和向西行进，第1次是向东，第2次是向西.此时可以将其理解为：当向东走完之后，向西的路程要超过向东，也就意味着向西行进要超过原点，最终位置在原点西侧5 米.由此得出算式：（+20）+（-25）=-5.

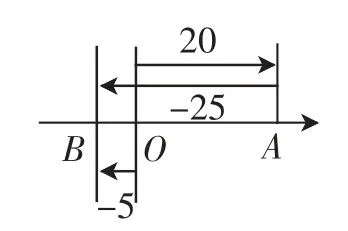
图4

对预设3、4而言，如果仅仅依赖于学生的自主讨论，很难准确把握这两种不同的情况.所以，在具体讨论的过程中，教师有必要深入其中，选择合理的契机，旁敲侧击给予启发.当然，启发应当点到为止，不管是画图还是具体的运算过程，都应当由学生自主完成.

预设5：假设a=0，b=-20，此时的运算过程可以利用算式表示为0+（-20）=-20，就此理解为：第1阶段没有移动，第2阶段向西行进20 米.

预设6：假设a=+20，b=0，由此可得出算式：（+20）+0=+20.

预设7：假设a=+20，b=-20，由此可得出算式：（+20）+（-20）=0.

预设8：假设a=-20，b=+20，由此可得出算式：（-20）+（+20）=0.

a、b同取值0的情况相对简单，在此处不做过多讲解.

教师活动：结合学生之前的讨论，对其进行完善和补充，以此形成最终的结论，然后对上述情形进行分类.以此得出以下三种不同的情况：

（1）同号相加：（+20）+（+15）=+35，（-20）+（-15）=-35.

（2）异号相加：（+20）+（-15）=+5，（+20）+（-25）=-5，（+20）+（-20）=0，（-20）+（+20）=0.

（3）含零相加：0+（-20）=-20，（+20）+0=+20.

学生活动：通过梳理和归纳，已经基本完成了雏形的架构，此时需要结合教师的引导，对具体的法则进行归纳及完善.

最终结果如下：

（1）如果相加两数为同号有理数，其结果取相同符号，相加的是绝对值.

（2）如果相加两数为异号有理数，还需要结合具体的情况进行以下分类：①绝对值不相等，其结果取绝对值较大的加数的符号，得数是用较大的绝对值减去较小的绝对值；②绝对值相等时，结果为0.

（3）对任何有理数而言，在与0相加之后，其结果仍然是这个有理数.

学生活动：教师为学生提供练习，由学生自主展开训练，目的是巩固法则、熟悉法则.针对练习的设计，应当能够涵盖所有的加法类型，也要有效控制题量，应当维持在8～10题，既能够实现有效的训练，也要确保不会占用较多的课堂时间.

教师活动：在带领学生归纳法则的过程中，应当突出强调其中的要点：其一，要针对两个有理数所有的符号类型进行判断；其二，为其匹配相对应的运算法则；其三，确定得数的符号，然后利用绝对值完成运算过程.

3 组织体验探索，深化法则认知

学生体验1：任意选择两个有理数，确保其中存在一个负数，将其填于○和□中，分别完成计算○+□和□+○，然后对比计算结果.

学生活动：上述计算过程应当由学生自主完成，然后尝试探索结论.经过学生的反复实践之后，发现任何一组有理数都能够满足○+□=□+○，由此也能够帮助学生形成认知：在有理数运算过程中，加法交换律同样成立，即a+b=b+a.

学生体验2：任意选择三个有理数，确保其中存在一个负数，将其填在○、□和◇中，在此基础上分别计算（○+□）+◇和○+（□+◇），然后对比计算结果.

学生活动：这一过程仍然由学生自主完成，尝试将有理数代入相应的位置，尝试进行运算，并尝试推导结论.对于任何一组有理数而言，都能够满足（○+□）+◇=○+（□+◇）.就此可表明，在有理数的运算过程中，加法结合律同样成立，即（a+b）+c=a+（b+c）.

学生活动：教师所设置的例题由学生独立思考、自主完成，在实际处理的过程中，教师应给予学生一定的启发，引导其灵活运用不同的运算规律，以实现对问题的简化和优化.结合教师的引导和总结，学生顺利完成课堂内容的归纳和梳理，具体如下：有理数加法运算法则及运算规律，展现数轴在加法处理过程中的具体作用.最后由教师布置作业，这样就能够将课堂学习顺利延伸至课外，实现更深层面的理解和认知.

以上是以“有理数的加法”为例展开的教学设计，通过合理的教学活动安排，既能够提高学生对实际活动的参与度，也能够主动探寻知识、发现知识，全身心投入其中.在这样的课堂中，学生所掌握的不仅是数学知识，也习得了数学方法及数学思想，还能够实现更有效的延伸和应用.