精选“数学好问题”，驱动拓展活动课——从一节九年级活动课的片段说起

☉江苏省无锡江阴市云亭中学 钱嘉蓉

全等三角形是八年级上学期的学习内容，随着全等工具的运用，平面几何就可以更方便地展开对很多特殊图形及性质的探究与发现，比如，特殊三角形（等腰三角形、直角三角形），平行四边形的性质与判定的研究，九年级圆和相似的研究，等等.可见全等的学习是具有奠基和全局作用的，是一种“好的数学”（陈省身语）.最近，在九年级学习圆和相似之后，笔者又安排了一节数学拓展活动课，引导学生运用圆、相似等知识继续研究与全等有关的条件，促进了学生对全等、圆、相似等平面几何知识的深刻理解.

1 从一节九年级活动课的片段说起

提出问题：在八年级曾研究过命题“全等三角形对应边上的高相等”，我们也知道这是全等三角形的性质，同学们当时已证明过.现在让我们对这个命题做一些变式，提出以下问题：

问题1：如图1、图2，在△ABC和△A′B′C′中，AD、A′D′分别是△ABC和△A′B′C′的高.如果BC=B′C′，∠BAC=∠B′A′C′，AD=A′D′，那么△ABC与△A′B′C′全等吗？

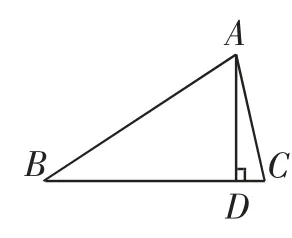
图1

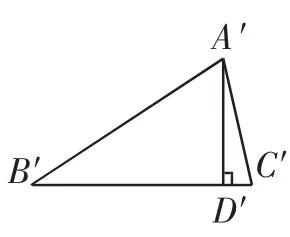
图2

教学记录：经过一段时间的思考，有学生提出证明思路1.

思路1：如图3，画出△ABC的外接圆⊙O，过点A作AA′∥BC，与⊙O交于点A′.连接A′B′（点B′与C重合）、A′C′（点C′与B重合），得到△A′B′C′.接下来进行证明.由AA′∥BC，得∠A′AB=∠ABC.又∠A′AB=∠A′B′C′，则∠A′B′C′=∠ABC.又因为∠B′A′C′=∠BAC，B′C′=BC，所以△A′B′C′△ABC.

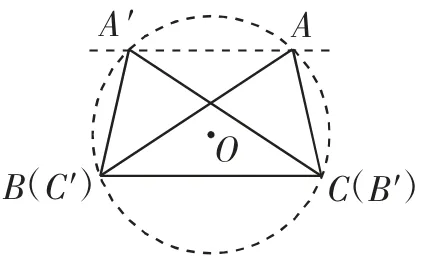
图3

思路2：如图4，将△A′B′C′进行图形变换，使边C′B′与BC重合.设A′B′、AB相交于点M，连接A′A.

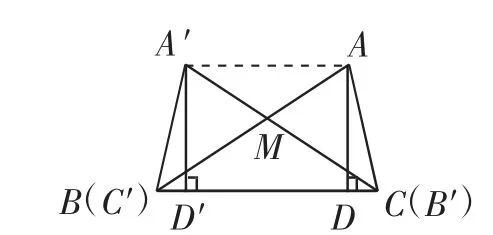
图4

结合∠BAC=∠B′A′C′，∠AMC=∠A′MC′，得△A′MC′△AMC，得比例式

由比例式①、②可得MC=MC′，则∠A′B′C′=∠ABC.又BC=B′C′，∠BAC=∠B′A′C′，所以△ABC△A′B′C′.

解后回顾：解决问题1的关键是将“分散”着的两个三角形“集中”到一起，然后运用圆的性质或相似三角形的性质，解决证明全等三角形的一个关键条件.

问题2：如图5、图6，在△ABC和△A′B′C′中，AD、A′D′分别是△ABC和△A′B′C′的高（AD＜A′D′），且∠BAC=∠B′A′C′，，求证△ABC△A′B′C′.

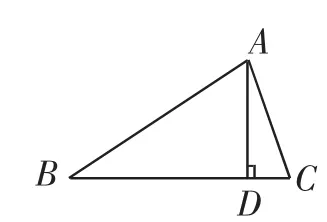
图5

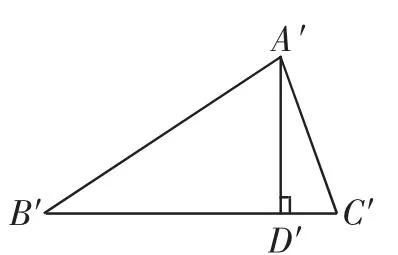
图6

教学记录：学生经过5分钟左右时间思考之后，仍然没有获得进展，于是我们给出以下方法启发.如图7，在A′D′上截取A′E=AD，过点E作FG∥B′C′.分别交A′B′、A′C′于点F、G.

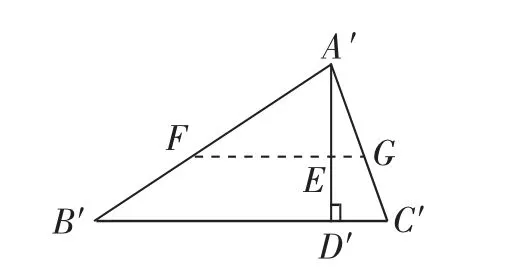
图7

在作辅助线之后，继续安排学生思考，很快有学生获得思路贯通.

由FG∥B′C′，可得∠A′EG＝∠A′D′C′，△A′FG△A′B′C′.结合A′D′⊥B′C′，可得∠A′EG＝∠A′D′C′＝90°，所以A′E⊥FG，即A′E是△A′FG的高.

在△ABC和△A′FG中，AD、A′E分别是△ABC和△A′FG的高，BC＝FG，∠BAC＝∠FA′G，AD＝A′E，由问题1的证明进展可知△A′FG△ABC，所以△ABC △A′B′C′.

解后回顾：解决这个问题的障碍在把“小三角形”集中到“大三角形”中，然后运用相似三角形的性质将问题2转化为问题1，实现问题解决.

2 关于拓展活动课的一些思考

2.1 拓展活动课需要精心选编学材内容

拓展活动课主要是拓展学生的理解，教材上的阅读材料、实验案例等都可以成为拓展活动课的素材，但是具体备课时，不应局限于教材上的素材，还可以查阅教师用书或其他数学史料，挑选适合本章内容或一个阶段学习内容的拓展素材，进行恰当选编，成为拓展活动课的学材，这也是“学材再建构”的一种体现.在选编学材时，还可关注一类“数学现实”，即在之前学习过程中遇到的一些较难数学问题，由于出现了新的数学知识或工具，则可以对这些“较难题”进行攻克，像上面提出的问题1，虽然是一个证明全等三角形的问题，但是成功解决却需要借助圆或相似等知识.这类问题的成功解决，让学生看到新工具、新知识的价值，将其作为作业安排给学生可能是偏难的，但作为拓展活动课的学材，师生共同探究是可行的.

2.2 拓展活动课可以基于问题驱动探究

基于问题驱动的数学教学设计是很多教师开展的课题研究，问题驱动要将习题变为问题，减少课堂上习题的数量，让问题的品质得到提升，有利于学生解题思维的聚焦和深入，促进对问题的深刻理解.在上面的课例中，我们精选了两个问题，驱动着这节数学拓展活动课的教学进程，学生在这两个有挑战的问题引导下，攻克难题的心理驱动着他们“安静的”思考，此时“无声胜有声”是这类活动课的又一教学特点.另外，两个问题之间也具有关联和递进的关系，学生在解决问题2时，问题2可以转化为问题1的已有进展，这是一种“看似并列，实则递进”的问题设计方式，当学生不能顺利转化时，可启发他们思考前一个问题带来的进展或性质，教学启发或教学干预的强弱可以根据学生的课堂反应灵活把握.

2.3 拓展活动课需要提前预设铺垫问题

拓展活动课一般都是安排在全章（或一个相对完整的单元）新知学习结束时进行，所以挑选的学习资源往往比较有挑战性，教师可基于学情的研判进行铺垫式问题的预设.铺垫式问题就像解题台阶一样，教学时应根据学生的已有进展或解题主要障碍，相机出示铺垫式问题，而不是根据课前预设“全盘托出”.比如，当学生对解题出发点还没有辨明时，可出示帮助他们继续审题、找准起点的铺垫式问题；又如，当学生解题目标不清时，可引导学生从问题待求证的目标“逆过来”思考，假设这个求证目标是成立的，能得到什么呢？还有，当学生不能突破思路中的关键步骤时，可以启发或出示一个之前学生曾练习过的同类问题，帮助学生回忆这类问题的解决策略（对几何经典问题来说，如如何添加某条重要的辅助线），然后学生在这类问题的启示下，再独立贯通思路，这时学生就会有解题成就感，不但能掌握这类问题的解法，而且在这个过程中会收获解题自信.

2.4 拓展活动课也要安排回顾反思环节

课堂小结对一节课来说非常关键，一个好的课堂小结能对本节课所学起到聚意点睛的作用，而那些泛泛而谈应付式的小结（比如，这节课你学到什么？你还有什么疑惑？）则可有可无.对拓展活动课来说，在课堂最后，要围绕本课研究内容进行必要的小结与回顾.比如，围绕研究问题之间的关联，请学生谈谈有怎样的认识；再如，围绕解题过程中的较难一步、关键步骤有怎样的认识或经验分享；还有，让学生就同类问题进行梳理，在组内先进行交流、归类，然后大组汇报，等等，这样的小结环节，能促进学生回顾本课所学、所思、所悟，教师鼓励学生交流、分享与展示，能达到较好的回顾与反思的作用.