某库岸开挖边坡卸荷岩体分析评价方法研究

白亚妮，胡习文，毛振凯，袁秋霜，陈兴周

(1.西安科技大学 建筑与土木工程学院,西安 710054；2.中国葛洲坝集团股份有限公司,武汉 430000；3.中国电建集团西北勘测设计研究院有限公司,西安 710065)

0 前 言

深切峡谷中陡峻岩质边坡的开挖，是中大型电站建设过程中不可避免的工程问题；且库区原生陡倾岩坡多数具有复杂的坡体结构及易于伴随工程活动产生卸荷变形的应力渗流环境。工程开挖与库水蓄泄是诱导开挖边坡发生变形甚或产生坍塌失稳的主要因素，结合岸坡结构与场区环境研究涉水岩质岸坡的变形破坏特征，可为工程设计优化及风险防范提供参考。陡高岸坡的开挖活动是诱导岸坡发生应力释放与形成开挖卸荷岩体及诱发卸荷扰动区裂隙网络贯通的根本因素。与河流潜蚀过程滋生的岸坡自然卸荷变形相比，工程建设导致的岸坡开挖卸荷岩体往往具有应力释放迅速、原生结构破坏显著且变形短时间突出的显著特点,即开挖卸荷岩体与紧邻岸坡原岩既存在结构性差异，更存在力学参数衰减特征，是岸坡非特殊滑面之外所需支护的重点对象，也是防范库水蓄泄过程产生渗透潜蚀作用的核心区域。关注岸坡开挖卸荷岩体的衍生机理及分析评价方法，既是合理评估开挖卸荷岩体范围及其稳定性研究所要解决的核心问题，也是实现预测开挖岩坡变形规律及服务工程设计的有效途径。因此，有必要结合库岸边坡结构与赋存环境及初拟开挖设计方案，开展岸坡开挖卸荷岩体分析评价方法及其在场区环境或工程活动干扰下长期力学特性与变形破坏机理方面的研究工作。

国内学者哈秋舲[1]于1997年首次提出了“卸荷岩体力学”概念，在此之前，工程开挖岩体问题的研究多数基于加载岩体力学理论，所得结论与工程实际观测结果很不一致。此后，诸多学者基于卸荷岩体力学理念，开展了多因素复合作用下岩体开挖卸荷变形机理及分析方面的研究工作。张永兴[2]提出了卸荷岩体力学分析方法—变刚度迭代法，通过取不同卸荷区域岩体力学参数有效模拟了岩体卸荷非线性特征。李建林等[3]通过室内试验研究了卸荷岩体的应力应变关系及变形参数随卸荷阶段的变化规律。周济芳等[4]研究得到随着卸荷量的增大，岩体的宏观力学参数衰减，岩体质量不断劣化的规律，为卸荷岩体力学特性的进一步深入研究提供了依据。刘泉声等[5]通过对高应力条件下花岗岩进行卸荷试验，得出卸荷过程中岩石横向变形剧烈、扩容显著，变形参数损伤劣化的规律与初始围压相关等结论。王兴霞等[6]应用卸荷岩体理论计算得到开挖边坡水平位移值是常规算法所得位移值的2～4倍，验证了边坡岩体工程采用卸荷岩体力学理论更符合工程实践情况。柏俊磊等[7]通过三维有限元模拟考虑岩体开挖卸荷作用的影响，对比分析了边坡模型的应力应变过程及塑性区变化范围。胡田飞等[8]以偏应力增量为主要评判指标，依托数值分析法确定了边坡开挖松弛区范围。刘爽等[9]基于岩体损伤力学理论，构建了考虑岩体材料非均匀性和损伤特性的边坡分步开挖卸荷数值计算模型，并通过案例分析给出了开挖过程中松弛区范围及松弛程度。陈兴周等[10]指出依据边坡岩体的卸荷量级对卸荷扰动岩体进行分区，并根据卸荷岩体分区结果提出加固及相应的支护方案。李宁等[11]提出边坡潜在滑动面力学参数最小取值准则，为有效进行边坡初始场岩体力学参数的遴选提供了思路。

本文采用室内试验和数值仿真研究方法，以对象边坡岩体为试样载体，开展室内常规三轴压缩及三轴卸荷试验；对比加载与卸荷过程中试样应力-应变曲线变化规律，获取试样卸荷量级与弹性模量降低百分比之间的相关性，为后续数值分析中岩体变形参数的确定提供参考；构建边坡分级开挖数值计算模型，依托地勘报告和数值计算结果开展初始场参数细化及遴选工作，并依据应力卸荷量开展开挖松弛区域划分与对应岩体力学参数取值及本构模型适应性对比；同时考虑支护设计及库水影响下岩体变形稳定问题，为岸坡开挖卸荷岩体分析评价提供参考。

1 室内卸荷试验

1.1 试验方案

结合地勘报告和工程类比手段，并参考GB/T 50266-2013《工程岩体试验方法标准》规范要求，将砂岩制备成50 mm×100 mm(直径×高度)的标准圆柱体岩样，表面无明显可见节理，整体完整性较好。为减小试验结果的离散性，对岩样进行了纵波波速测定，并剔除结果异常的岩样，选定岩样如图1所示。

图1 试验岩样

采用岩石THMC多场耦合三轴流变测试系统，针对试验岩样分别开展不同围压下(8、12、16 MPa)的三轴压缩及三轴卸荷试验。综合实际工程坡体开挖强度及三轴压缩试验结果，选取不同围压下三轴峰值抗压强度的70 %作为卸荷试验的轴向应力水平；并从边坡开挖过程岩体应力环境入手，三轴卸荷试验的应力路径最终选定为恒轴压卸围压。

1.2 变形参数特征分析

依据室内试验结果，绘制了8、12、16 MPa围压下常规三轴压缩及三轴卸荷试验的应力-应变关系曲线，如图2所示。

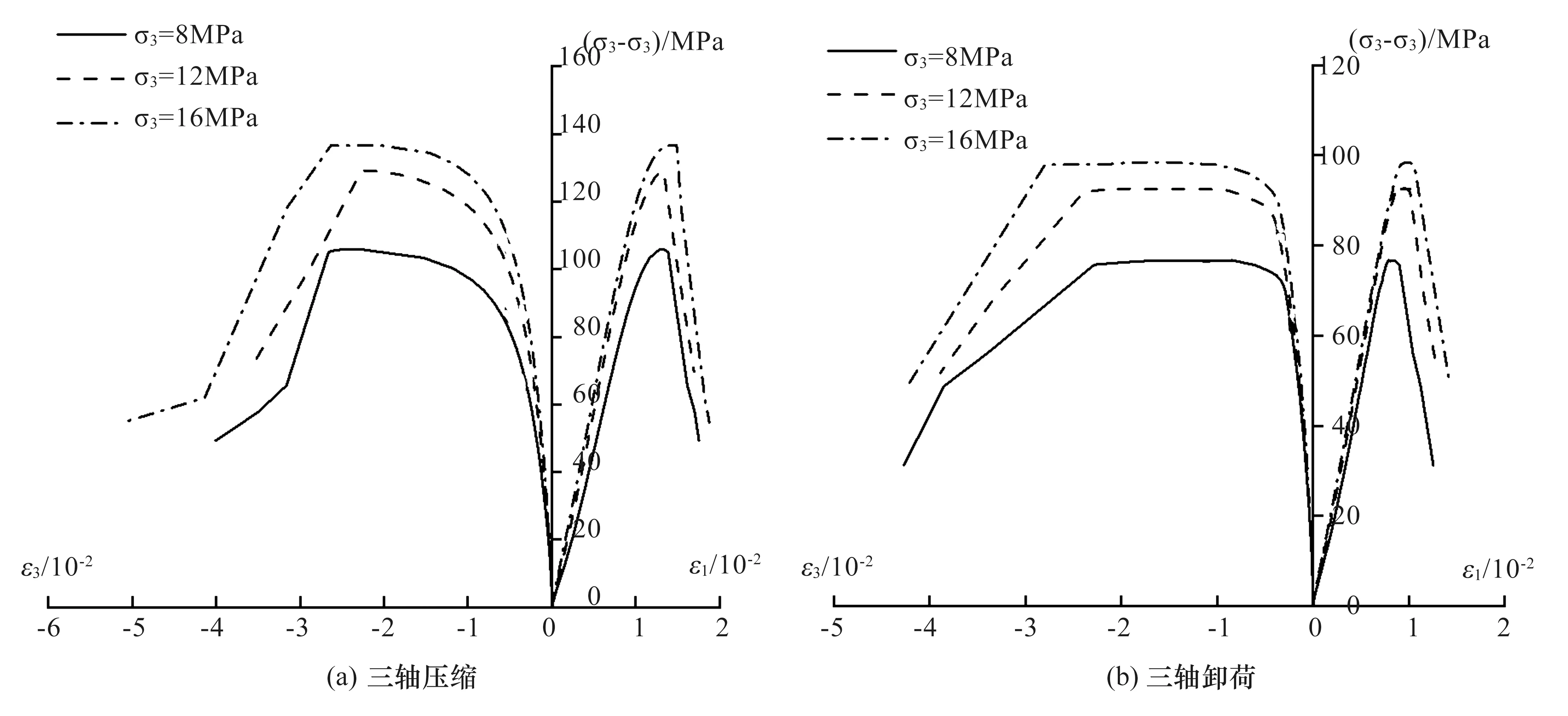
图2 不同应力路径下应力-应变关系曲线

三轴压缩试验结果表明，随着初始围压的增加，岩样的峰值抗压强度逐渐增大，主要因围压对试样环向变形约束越大，对新生微裂隙发育的抑制作用、对原有微裂隙扩展的束缚作用越明显，故承载能力有所增强。卸荷试验结果表明，不同围压下卸围压过程中试样环向应变增长迅速；围压越高，卸荷过程中环向变形越大。究其原因在于模拟开挖方式的同等卸荷速率条件下，试样初期应力环境越高，卸荷过程中应力释放量级越大，类似于为试样环向承受拉剪作用提供了更大荷载，从而导致了试样环向微裂隙的迅速滋生、扩展、贯通。因此，试样卸荷破坏主要因环向扩容显著所致，加载破坏主要因轴向压缩变形较大所致。

依据三轴卸荷试验结果可知，初始围压水平一致时，试样弹性模量随卸荷量的增加而减小，且随着卸荷量级的增大，弹性模量降低百分比增量急剧增加，主要因围压卸载引起试样强烈的卸荷回弹变形及沿卸荷方向张性扩容，进而导致力学性质劣化。

不同初始围压下卸荷量与试样弹性模量降低百分比关系见表1。当卸荷量小于40 %时，弹性模量降低约5 %以内；卸荷量在40 %至80 %，弹性模量削减量在5%～14%；大于80 %时，由于岩样环向扩容显著、变形急剧增加，处于结构性破坏状态，内部裂隙贯通，试样的力学性质大幅度劣化，弹性模量降低约60 %。

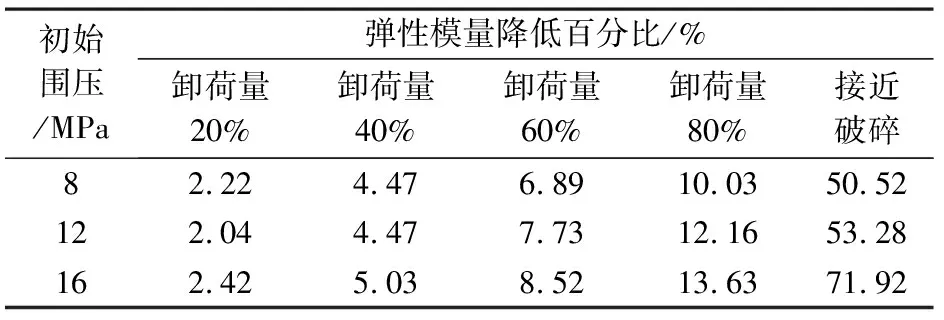
表1 不同初始围压下卸荷量与弹性模量降低百分比关系

结合表1试验参数特征，针对边坡分步开挖计算模型，以围压卸荷量为60 %和岩样接近破碎时所对应的弹性模量削减百分比作为初步参考值，以模拟边坡分步开挖过程中产生的不同卸荷松弛影响区域对岩体力学参数的影响，实现边坡开挖过程中变形参数的遴选匹配。

2 模型构建与参数遴选

2.1 模型构建

依据工程地质剖面图构建边坡分级开挖模型，模型总高度为150 m，宽度290 m，坡顶至坡脚采用台阶式放坡开挖，共分5级开挖。采用生死单元算法模拟边坡分步开挖，选取四节点四边形单元进行网格划分，共划分为12036个单元、12212个节点，其中坡面网格划分密集，远离坡面的区域划分相对稀疏，并在坡面和坡体间采用过渡单元，以减小计算结果产生的误差。

模型底部为固端约束，两侧为水平约束，坡面为自由边界，允许其发生变形；整个计算过程只考虑坡体自重作用，忽略构造应力和外部载荷的影响。本构模型采用理想弹-塑性模型，屈服准则选取Mohr-Coulomb准则和Drucker-Prager准则对比分析。

数值计算模型及监测点布置如图3所示。为了更加直观反映随边坡分步开挖，卸荷效应对坡体变形的影响，沿坡面从上至下布置4个监测点，编号依次为1～4号。主要选取位于第四级边坡中部的监测点3号为例进行数值计算结果讨论。

图3 数值计算模型及监测点布置

2.2 参数遴选

岩体力学参数的选取极大的影响数值计算结果，也是决定计算结果是否符合工程实践的关键因素。本文主要依托已构建的边坡初始场模型，以李宁等[11]提出的潜在滑动面力学参数最小取值原则为思路及地勘报告所建议的岩体力学参数范围为参考进行试算。计算结果分析如下。

图4为初始场应力矢量分布图。由图4可知，坡面附近最大主应力方向与坡表近于平行，最小主应力与坡面近于垂直。随边坡深度的增加，任一点最大、最小主应力增大且方向互相近于垂直，即深处岩体应力分布近似处于静水压力状态。

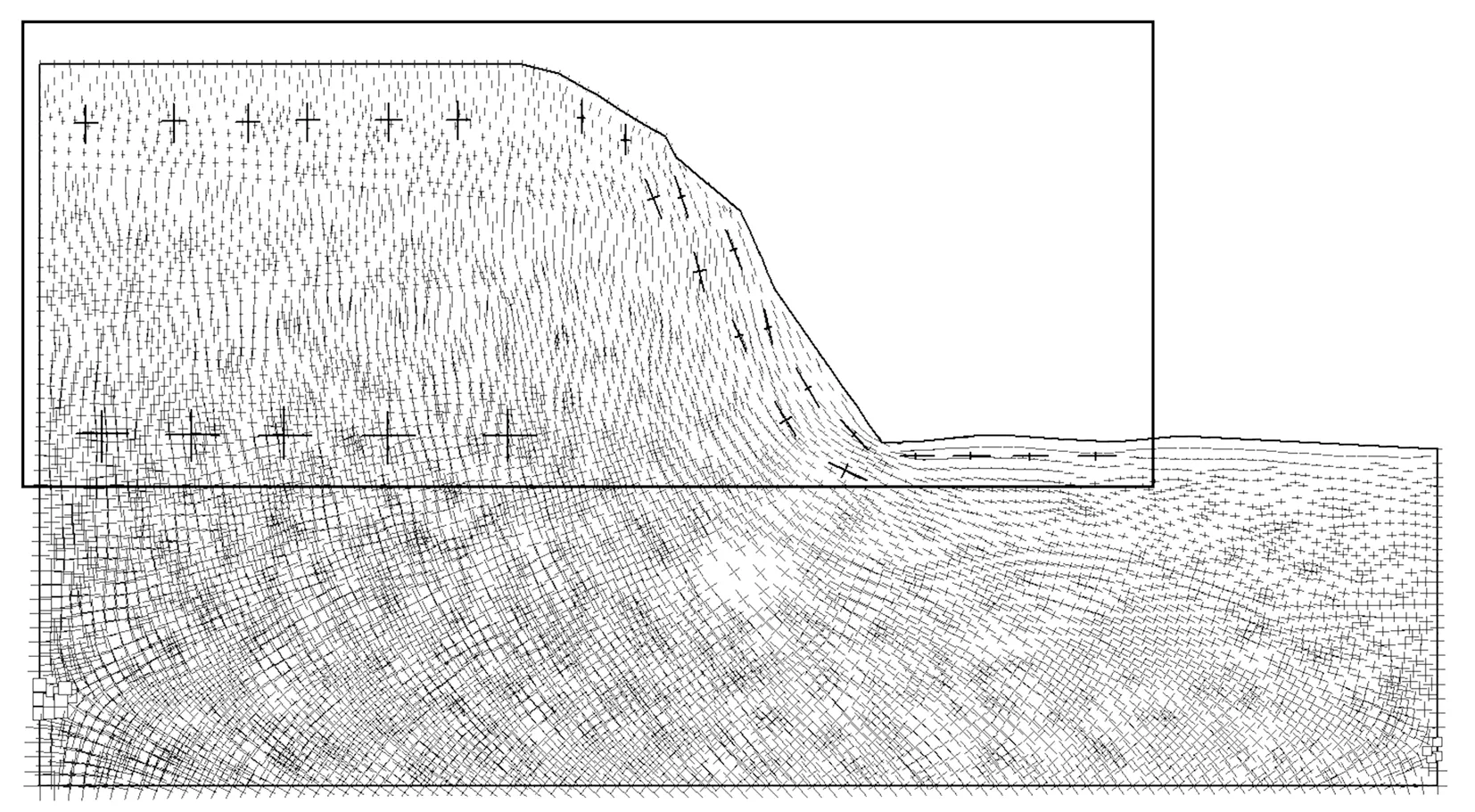
图4 初始场应力矢量分布

图5为初始场剪应变等值线图。自然环境下边坡坡体表面岩体风化剥蚀较为严重，故剪应变较大值主要集中在坡面中上部和坡脚位置处，此时剪应变区域尚未贯通，坡体深处剪应变值较小；自然状态下经过长期的地质构造作用，边坡处于稳定状态。

图5 初始场剪应变等值线 单位：%

结合初始场应力应变试算结果，以地勘报告岩体参数范围为参考，遴选确定出基本吻合对象边坡的岩体力学参数，如表2所示。

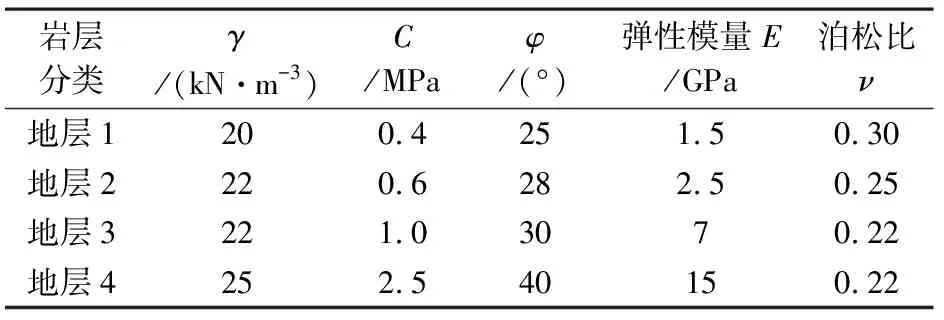
表2 Mohr-Coulumb准则下试算确定的初始参数

为探讨不同本构模型对开挖卸荷岩体的适用性，采用关联法则推导出与M-C准则匹配的D-P准则参数计算公式，如下所示：

(1)

(2)

公式(1)～(2)中：k、α为材料常数；c为黏聚力, MPa；φ为内摩擦角,(°)。

依据表2所得参数，利用公式(1)和公式(2)，计算得出Drucker-Prager准则等效参数，如表3所示。

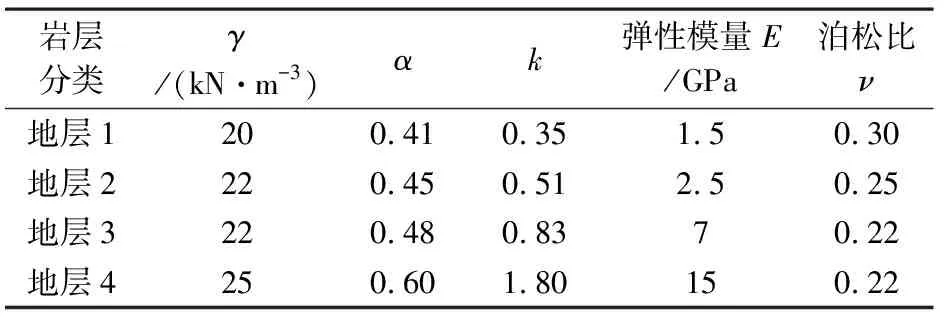
表3 Drucker-Prager准则下的等效参数

2.3 边坡开挖卸荷分区试算

边坡在长期地质构造作用下处于稳定状态，工程开挖扰动造成坡体局部岩体应力释放，应力发生重分布，临近坡表岩体逐渐向临空面移动、发生变形及破裂，随着分步开挖的进行，其变形破裂程度由开挖面向坡内逐级递减，岩体的力学性质也由于应力释放量不同而发生不同程度的劣化[12]。由于边坡开挖的进程导致坡体不同区域卸荷程度不断变化，即岩体的卸荷模拟应该是一个不断调整的动态过程；因而在数值分析中，需根据边坡开挖卸荷扰动程度，对应将坡体不同卸荷区域取与之对应的岩体力学参数，以实现吻合工程开挖实际情况。

室内三轴卸荷试验结果表明，试样弹性模量随围压卸荷量的增加而折减，说明卸荷量与开挖岩体的力学性质有一定联系。参考王瑞红等[13]研究提出的通过比较开挖前后应力场变化，将降低比值相同的区域划分为岩体同一开挖卸荷带思想，即利用应力卸荷量构建考虑岩体开挖卸荷应力松弛效应的数值计算模型。

假设开挖前边坡岩体所受应力为σa，开挖后的应力为σb，则应力变化百分比Δσ表示为：

(3)

通过公式(3)可将应力变化百分比相同的区域划分为同一开挖卸荷带，根据应力变化值从高到低将边坡岩体划分为强卸荷区、弱卸荷区和原岩区。

依据室内试验所得变形参数特征，对应取应力变化百分比为50 %和10 %作为依据划分出强、弱卸荷区域。针对强、弱卸荷区域岩体弹性模量分别降低50 %和10 %，主要依托有限元分析软件内置方法实现边坡开挖对强弱卸荷影响区内材料参数的动态折减，以模拟边坡开挖卸荷过程，使其更加吻合工程开挖实际情况。

3 边坡开挖卸荷数值计算结果分析

3.1 分步开挖进程应力应变分析

(1)位移分析

工程岩体随开挖卸荷进程损伤逐渐累积，近坡面处岩体由于应力释放，不断滋生微小裂隙，且张开微裂隙不断形成、扩张，直至最后贯通，岩体破碎，承载力下降。图6为开挖过程卸荷分区后水平位移净增量变化图，由图可知，水平位移增量较大值主要分布在近坡面中下部，坡脚位移增量最大；主要因岩体的风化程度随埋深的增加而减小，岩层稳定性逐渐向好，故远离开挖面位移增量较小。靠近坡面中下部位移等值线连续，而靠近边坡开挖第一级台阶处，等值线出现明显变化，主要因岩层交界面处岩体性质差异较大导致。

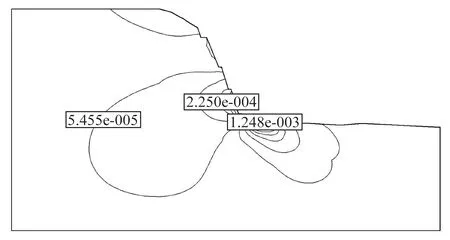
图6 水平位移净增量变化 单位：m

室内卸荷条件下，岩样破坏形式通常为形成贯通的剪切破裂带，此时，剪应变可反映岩体破坏程度。图7为开挖完成后坡体剪应变等值线图。由于对岩体力学参数按卸荷扰动程度的不同进行了折减，靠近坡面为强卸荷区域，故开挖完成后边坡表面变形影响范围增大。较初始场剪应变分布图，开挖面附近剪应变等值线几近贯通，且主要在坡顶、坡面中下部分布较为集中，为张拉破坏；坡脚剪应变分布最为密集，且数值较大，为压剪破坏。

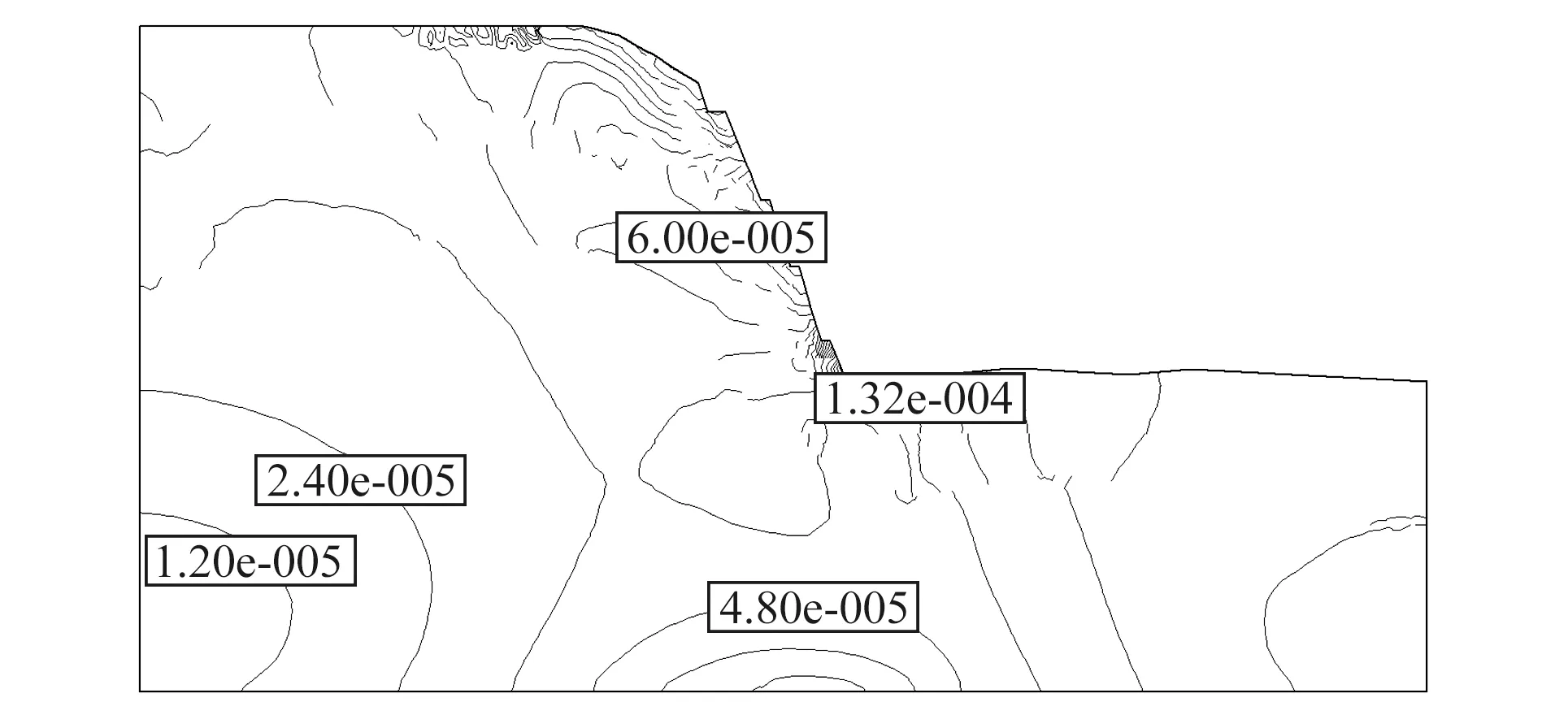
图7 开挖完成后剪应变等值线 单位：%

图8为监测点3号随开挖水平位移净增量图，从第2步开始进行第一台阶坡体开挖，水平位移增量随分级开挖呈增长趋势；12步开始开挖第四级台阶，故越靠近开挖面，扰动程度越大，位移增量越显著。综合分析，工程开挖中采用考虑卸荷松弛效应对岩体力学参数进行动态调整的计算方法，所得结果对优化工程设计和风险防范更具有参考意义。

图8 监测点3号随边坡开挖水平位移净增量

(2)应力分析

随边坡分级开挖，初始场应力受到扰动，距开挖面距离不同，应力释放量不同。因只考虑自重应力的影响，故上覆岩体的开挖，使第三主应力总体呈下降趋势。

监测点3号第三主应力变化趋势如图9所示。开挖级数越多，开挖面附近应力变化越明显，卸荷松弛效应也更加显著，第三主应力减小；岩体开挖卸荷回弹导致局部坡体开挖面附近产生拉应力，即第14步开挖以后，岩体应力由压应力转为拉应力状态，应力值为负。依据室内卸荷试验，可知岩体的承载力下降，脆性特征增加，从侧面反映了边坡抗滑力随工程开挖不断减小，边坡整体稳定性下降

图9 监测点3号随边坡开挖第三主应力变化

3.2 岩体开挖下M-C与D-P准则结果分析

Mohr-Coulomb屈服准则能较好地描述岩土材料的强度特性，在岩土工程领域得到了广泛的应用，但计算时忽略了中间主应力对破坏面的影响，且其屈服面在π平面上为不等角六边形，存在尖顶和棱角，数值计算存在一定困难。Drucker-Prager准则屈服面在π平面上为圆形，表述简单且数值计算效率高[14]。针对其各自的优缺点，通过对比边坡开挖卸荷下选用两种屈服准则的计算结果，验证摩尔匹配D-P准则在边坡开挖工程中的适用性。

图10为两种屈服准则下监测点3号水平位移净增量对比图。图10表明，D-P准则计算得到的位移增量普遍略大于M-C准则的计算结果，主要由于摩尔匹配D-P准则屈服面为M-C屈服面的内切圆，计算时低估了材料的抗屈服能力，因此屈服区较大，且不存在尖顶处数值计算问题，故计算结果略大。图11为两种屈服准则下计算迭代次数对比。D-P准则较M-C准则总迭代次数略多，各步迭代次数分散更加均匀，收敛更快。对于数值分析而言，屈服准则表述越简单，计算越易收敛，计算时间越短。结果表明，选用D-P屈服准则计算时间为26 s，选用M-C准则计算时间为55 s，时间缩短至一半，但结果相差不大。综合分析，说明摩尔匹配D-P准则具有一定的可信度，在数值模拟边坡开挖卸荷分析中，根据实际需求可采用D-P屈服准则，提高计算效率。

图10 两种屈服准则下监测点3号水平位移净增量对比

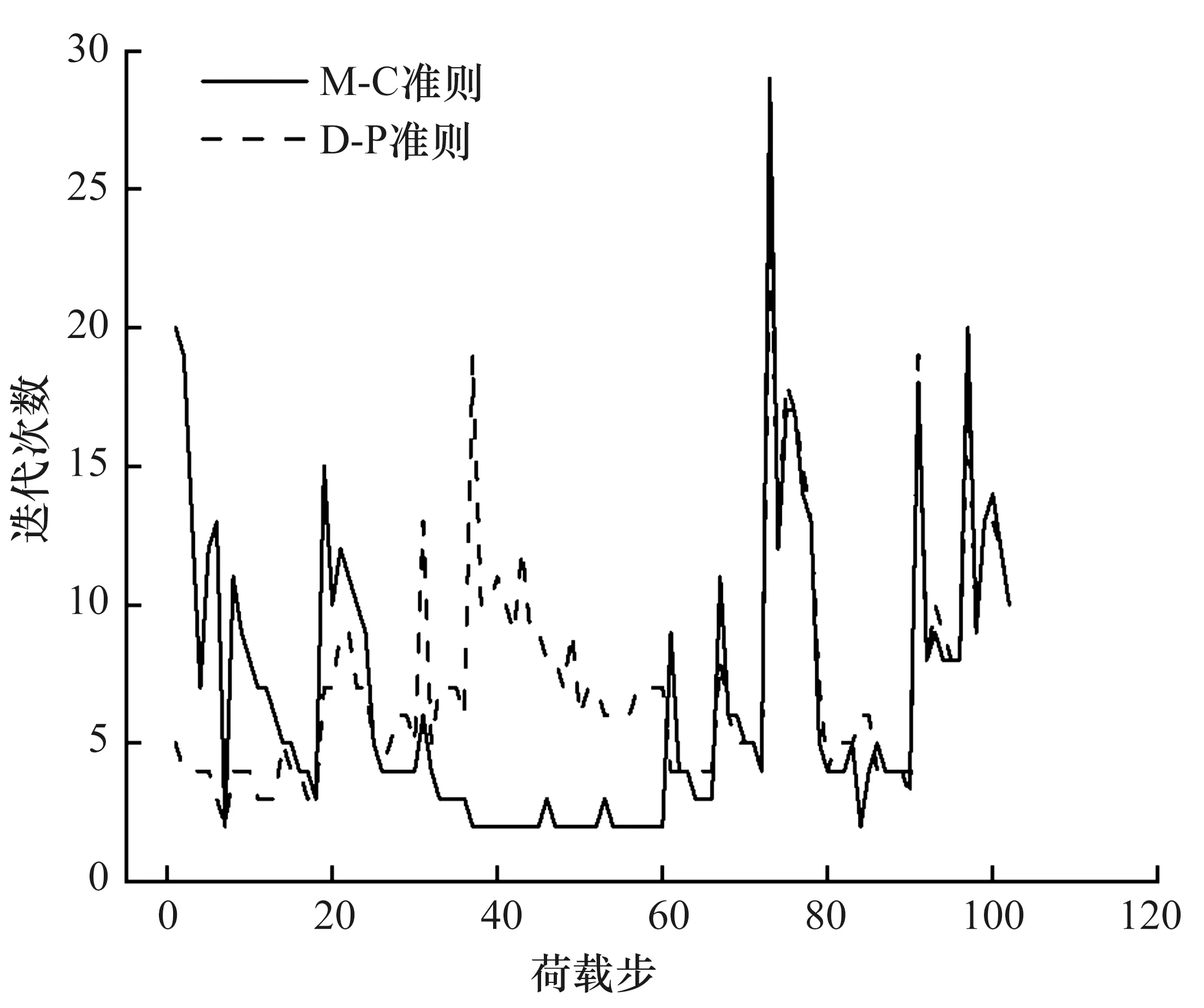
图11 两种屈服准则下计算迭代次数对比

4 开挖支护与蓄水下数值计算结果

结合边坡分步开挖划分的卸荷带区域，对边坡岩体采用锚杆和锚索联合支护。图12为开挖支护前后监测点3号水平位移净增量对比图，由图可知，边坡岩体仅开挖下变形趋势最显著，随分级开挖的进行变形迅速增大；对边坡岩体边开挖边进行支护，因加固措施改变了边坡开挖应力场，减小了其卸荷量，故水平位移净增量有所减小。

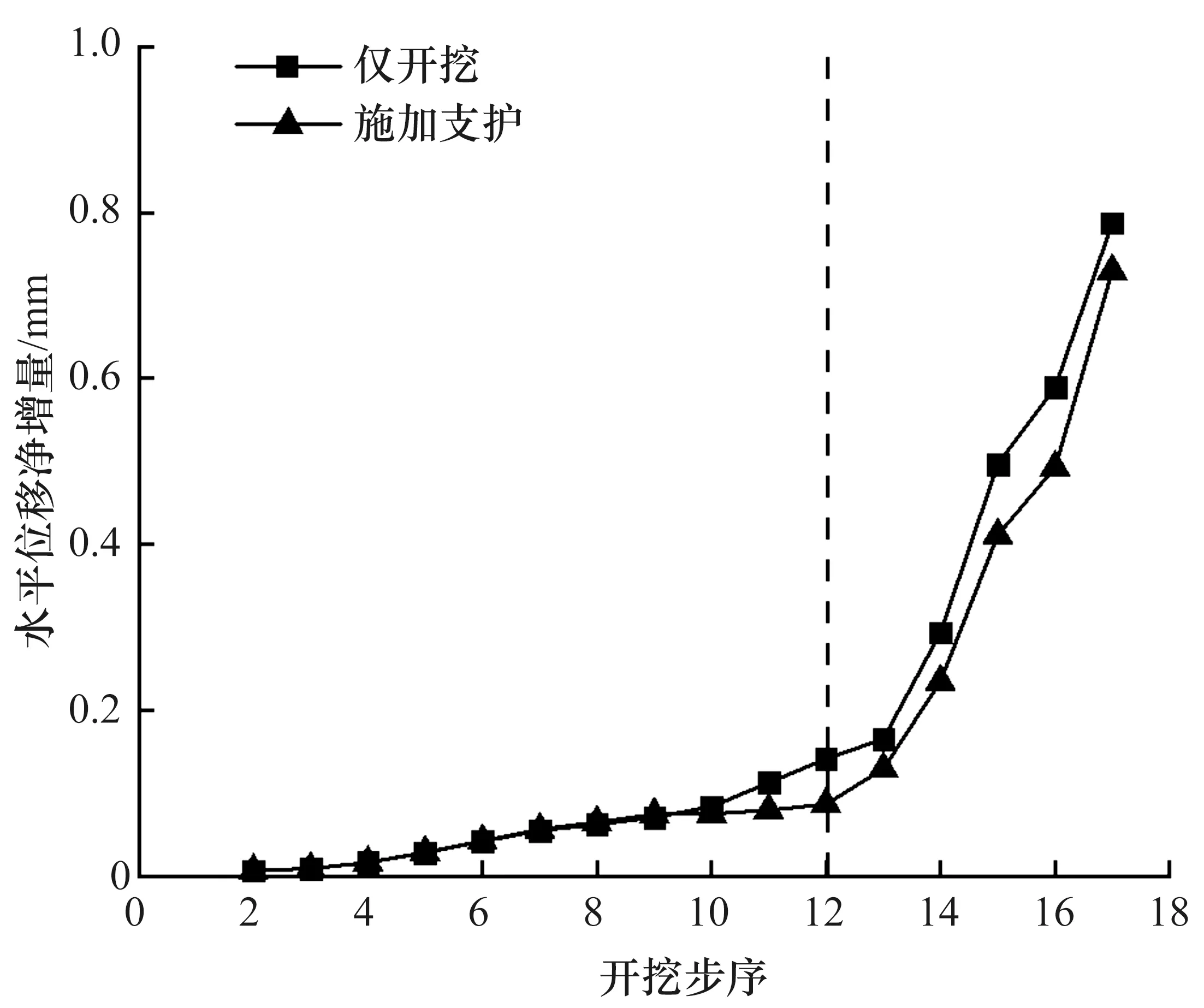
图12 支护前后监测点3号水平位移净增量对比

水库蓄水后，库岸边坡受力状态发生改变，随着蓄水高度的增加，边坡岩体在水的软化作用下，矿物联结力降低，导致抗剪强度下降，变形增加。

图13为监测点3号在蓄水前后水平位移净增量变化图，随水库水位的增加，边坡变形增大，尤其在边坡岩体开挖完成后至水库开始蓄水至正常水位时位移净增量幅度最大，可见蓄水对边坡变形影响显著。因此，对于水电站库岸边坡考虑水库蓄水影响下边坡的变形特征，具有实践意义。

图13 蓄水工况下监测点3号水平位移净增量变化

5 结 论

本文以库岸工程地质剖面及开挖边坡卸荷岩体为对象，结合室内卸荷试验参数特征分析，构建了考虑卸荷效应的边坡分级开挖数值计算模型，分析了开挖卸荷对坡体变形的影响及库水作用下边坡的变形特征，并研究了M-C与D-P准则在卸荷岩体分析中的适用性，形成结论如下：

(1)开展室内试验，界定了不同卸荷量级下变形参数取值范围，随围压的降低，弹性模量发生不同程度的削减。卸荷作用诱导岩样沿卸荷方向发生卸荷回弹变形、裂隙张性扩容以及产生一定量的拉剪裂隙，使变形参数呈现出非线性劣化特征。

(2)边坡开挖岩体随应力释放和应力重分布，卸荷损伤逐渐累积，其中不同卸荷范围影响区内的岩体力学参数发生不同程度的弱化。根据开挖前后边坡应力场变化特征划分卸荷带，且卸荷分带区域可为边坡支护范围及变形预测提供参考。

(3)开挖岩体变形显著，近坡面最大剪应变区域逐渐贯通。随开挖边坡的进行，坡面最小主应力释放诱导坡面岩体结构松弛，局部产生拉应力，但坡脚主要为压应力集中带。

(4)采用摩尔匹配D-P准则和M-C准则分析计算结果相差不大，说明该准则具有一定的可信度，并且计算时间较短，迭代次数多，计算效率更高。考虑边坡支护与蓄水下边坡变形计算成果，对于边坡岩体变形预测具有重要的实践意义。