滑带土强度参数选取
——以白龙江水泊峡水电站Ⅶ号滑坡为例
寇甄涛,刘荣清,张莉媛
(中国电建集团西北勘测设计研究院有限公司,西安 710065)
0 前 言
滑带土的赋存环境在时间和空间上均具有差异性[1-2],固结时间的长短和沉积条件的差异将直接影响岩土体的密度、孔隙、含水率,不同部位的滑带土受形成条件的影响,其物理力学性质也不尽相同。而滑带土强度、性质的差异必然导致滑坡的变形特性有所不同,进而影响滑坡整体的演变过程[3]。
滑带土的强度对滑坡的稳定性与变形评价影响重大,因此,被诸多学者关注。关于滑带土的性质与强度,有关学者已进行大量相关研究。闫玉平[4]基于滑带土的强度参数,利用有限元对滑带土进行抗剪强度分区。郑莉[5]认为联合水库右岸岩质滑坡体的滑带取样困难,分别采用重塑试验法、结构再生法、反演分析法提出了滑带土的参数建议值。赵宝平[6]人通过数值模拟手段研究了模型抬升角度与滑带土力学参数降低之间的关系。此外,在不具备室内试验的前提下,采用颗粒流模拟也逐渐成为获取滑带土强度参数的一种新方法[7]。
岩土体参数的选取在工程实践中具有重要作用,科学合理的选取参数是勘察设计中工作的重要组成部分。在试验参数选取方面,李鹏[8]认为在原位试验资料不足的情况下,经修正后的GSI指标可用于选取岩体力学参数。杨期祥[9]利用原位直剪试验、室内试验、工程类比法等手段综合确定了滑带土的力学强度参数,为大型深层滑坡滑带土的强度参数选取提供了借鉴。
如上所述,滑带土的强度与性质直接影响滑坡稳定性与变形的评价,如何准确地量化滑带土的强度参数是滑坡评价工作的重点。本文以白龙江水泊峡水电站Ⅶ号滑坡为研究对象,依托大量滑带土的试验数据,筛选出主控因子后采用数理统计方法建立预测模型,为合理推测力学参数提供支撑。
1 参数选取思路
岩土体的形成条件与赋存条件对其力学性质有着直接的影响,直观表现为物理性质的不同导致强度参数也有所差异。因此,如何通过物理指标合理选取力学指标对滑坡参数的确定具有重要意义。
在实际勘察工作中,获取各种赋存条件下滑带土的物理指标与力学指标对于查明二者之间的关系十分重要。对于规模较大或者危害性较大的滑坡,若条件允许,尽可能分段、分组取样,并增加试验组数。岩土试样群的干密度ρs、含水率ω及孔隙比e应囊括工程区内所有可能出现的情形,为科学分析滑带岩土体物理指标与力学指标的关系建立丰富的数据基础。
本文所研究的参数选取方法为:在获取大量滑带土试验参数的基础上,筛选对岩土体力学性质影响较大的物理指标作为主控因子,将力学参数(c值、φ值)作为目标参数,采用数理统计手段拟合出合适的回归方程。在已知各项物理参数的条件下即可合理预测岩土体的力学指标,整体思路如图1。
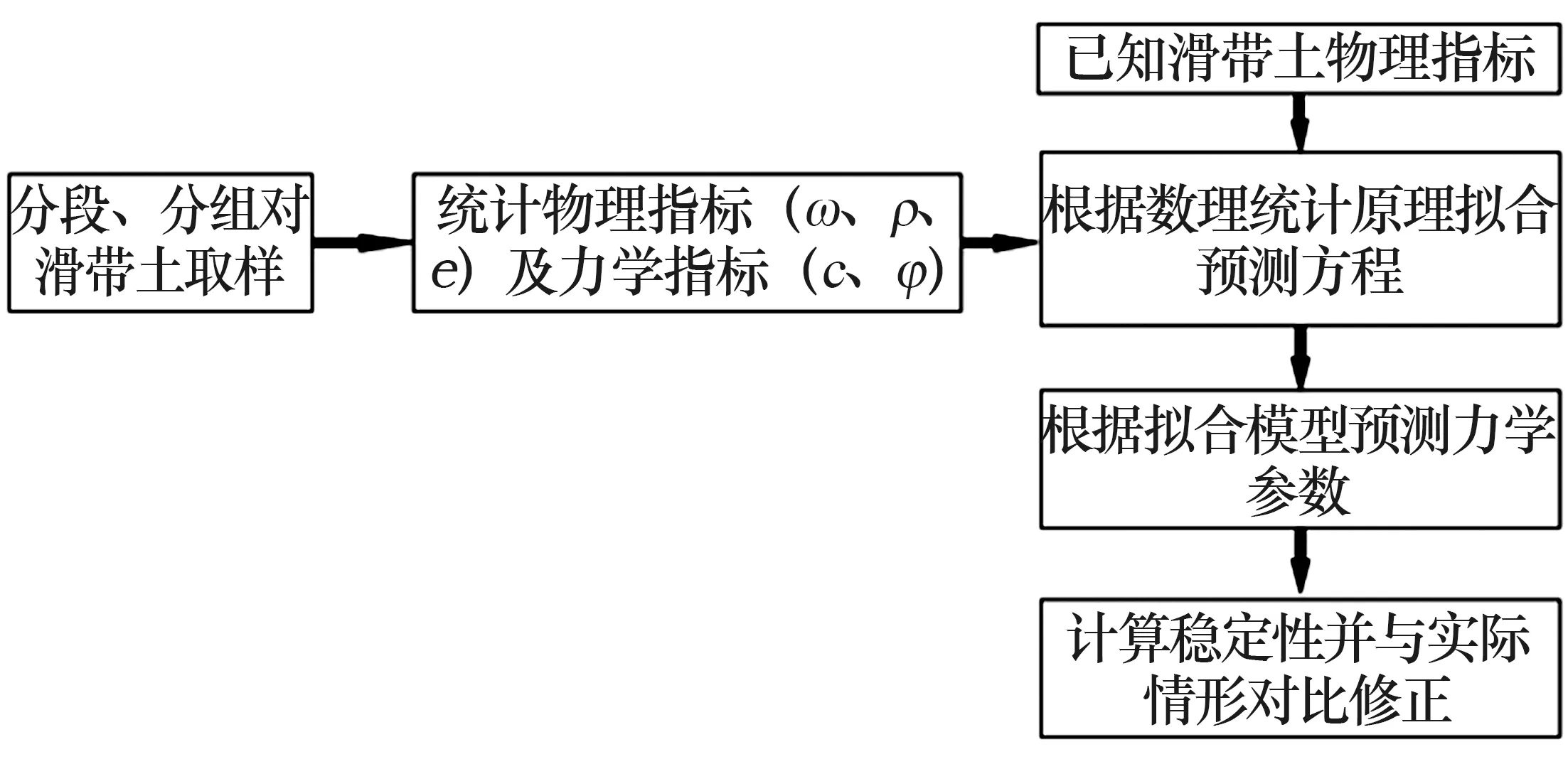
图1 参数选取思路流程
2 滑坡工程地质条件及概况
本文选取白龙江水泊峡水电站Ⅶ滑坡为研究对象,按照上述研究思路获取滑带土的力学参数,作稳定性分析后与实际情形进行对比,以验证上述参数选取方法的可行性。
Ⅶ号滑坡位于水泊峡峡谷左岸,白龙江自西南方向流入,滑坡区平面如图2所示。滑坡整体高陡,平均坡度30°~50°。滑坡前缘为白龙江III级阶地,阶地以下为河槽地貌,阶地以上河谷呈“V”字型。区内出露的基岩为志留系中上统薄板状绢英千枚岩夹板岩,产状NW290°~330° SW(NE)∠30°~50°,滑坡前缘部位发育有河流Ⅲ级阶地堆积的含漂砂卵砾石层和崩坡积层。区内断裂不发育,局部发育数条小断层。区内地下水活动不强烈,主要为覆盖层孔隙性潜水和基岩裂隙水。

图2 滑坡区平面
滑坡在平面上呈上小下大的喇叭状,东西两侧边界沟槽发育,后缘具明显的圈椅状。坡体最高高程为2 395.00~2 405.00 m,前后缘高差618.00~624.00 m,平均坡度30°~50°,主滑方向185°。坡体形态较完整,坡体上发育3条顺坡向冲沟。沿河方向滑坡宽约530 m,从前缘至后缘长约1 063 m,钻探揭露滑体最厚约115 m,总体积约3053×104m3,属巨型岩质滑坡,Ⅶ号滑坡滑坡全貌如图3所示。滑体主要为倾倒折断的岩体,表层为薄层崩坡积碎石土,滑动带主要为具一定胶结的块碎石土。

图3 Ⅶ号滑坡滑坡全貌
“5·12”地震发生后,滑坡发生明显变形,上下游侧、后缘以及前缘局部地段因滑动形成明显的锯齿状拉裂缝和剪裂缝。根据现场地质调查,滑坡目前处于整体稳定状态,仅前缘局部有小规模掉块、坍落。
3 预测模型
水泊峡水电站Ⅶ号滑坡为巨型岩质滑坡,一旦发生滑动,大量土石将填塞河道,并对水电站的安全造成威胁。因此,准确分析评价滑坡的稳定性至关重要。为全面了解滑带土的物理力学特性,勘察期间分别在上下游剪出口、后缘和坡体平硐内取粗粒土样共33组,适当去除大粒径后,依照土样原始赋存环境重制出物理指标与现场岩土体接近的重塑土样,然后进行试验,试验结果如表1所示。
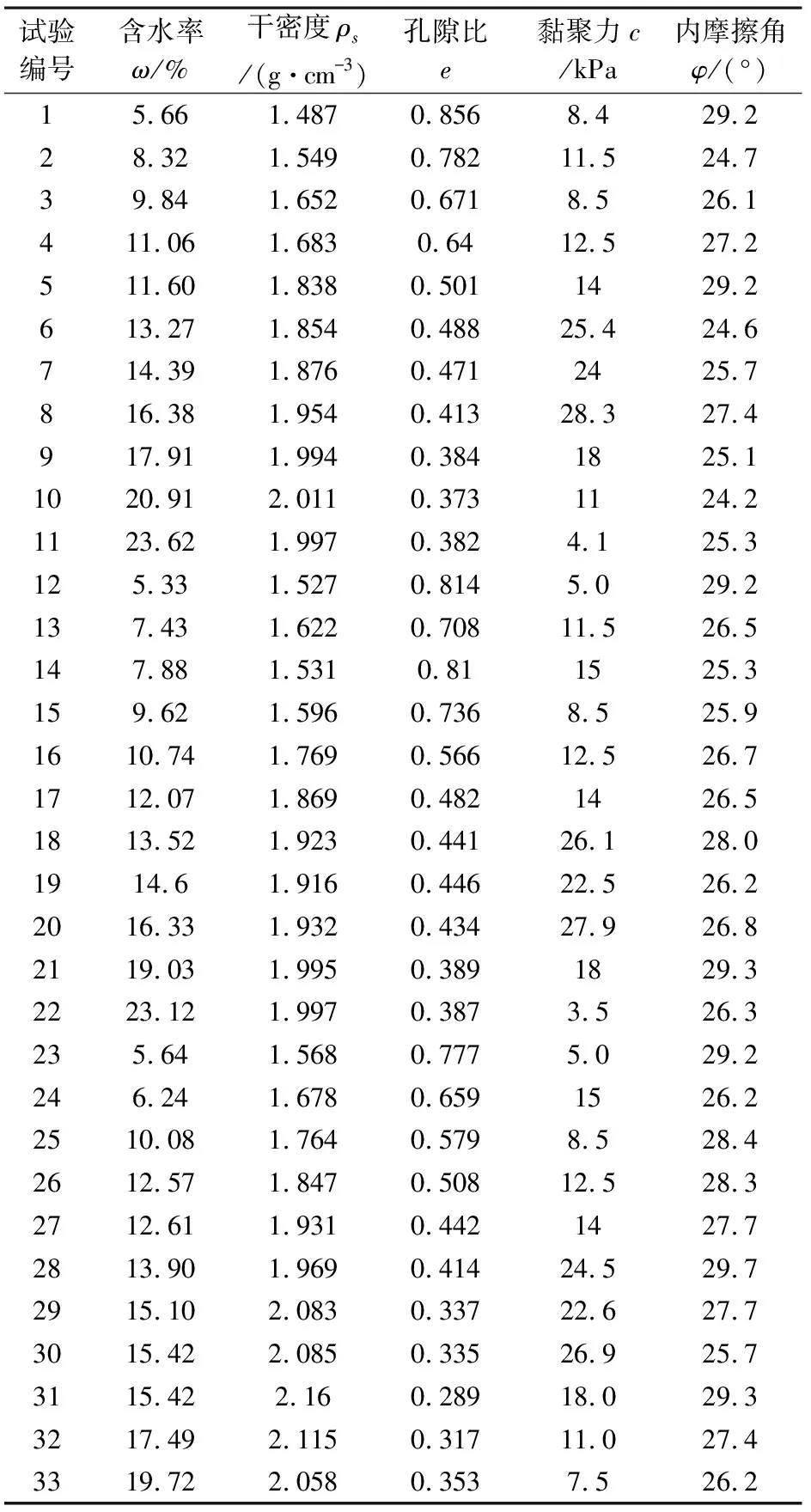
表1 滑坡滑带土试验数据
在获取原始试验数据的基础上,需要运用数理统计知识对上述数据进行处理分析,从而拟合出接近原始数据的趋势函数,建立预测模型。本文所研究的滑带土样本中,物理指标包括含水率ω、干密度ρs及孔隙比e,将上述3项指标作为主控因子,并作为预测模型的自变量。力学指标为黏聚力c与内摩擦角φ,作为本次预测模型的因变量。
3.1 拟合原理
根据自变量与因变量的函数关系,预测模型的拟合可分为多元线性拟合和多元非线性拟合。
3.1.1多元线性拟合
建立多元线性回归模型时,各变量应满足以下3个条件:
(1)自变量与各因变量的分布趋势应近似符合线性关系;
(2)各种条件下的因变量预测值应相互独立;
(3)残差ε应符合正态分布。
假定因变量Y与自变量X1、X2、X3,…,Xm存在如下关系:
Y=β0+β1X1+β2X2+…+βmXm+ε
(1)
公式(1)中:β0为常数项;β1、β2,…,βm为偏回归系数,其数学意义为Xi变化一个单位时,Y的平均该变量;ε为残差。

(2)
(2)式方程组中:
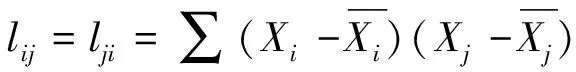
(3)

(4)
在上述方程组求解完成后,再求解常数项b0,见公式(5)。
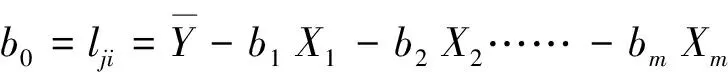
(5)
3.1.2多元非线性拟合
多元非线性拟合较多元线性拟合而言,计算更为复杂,其本质仍是寻找拟合函数值与样本值的误差平方和最小的函数模型[10]。由于脱离了线性条件的束缚,各自变量与因变量的关系并不明朗,可能存在多种近似关联。因此,解决此类问题时,一般常用的手段为根据对拟合关系的已知理解给定基本拟合模型,然后通过统计方法求得各项参数。由于非线性拟合计算体量较大,因此,一般借助计算机或者专业的统计软件完成计算拟合。
3.2 拟合结果
基于上述理解认识,对本文中的滑带土试验样本进行拟合,分别进行多元线性回归拟合与多元非线性回归拟合,选择出更贴近样本原值的回归模型。
如前文所述,含水率ω、干密度ρs、孔隙比e3项物理指标对岩土体的力学性质影响较大,因此将其作为控制岩土体强度的主控因子,并选择为本次拟合的自变量,对应的强度参数c和φ为因变量。
从表1中试验数据可发现,由于滑带土为粗粒土,颗粒间内摩擦角较大,且分布均匀,可见物理指标的改变对摩擦强度的影响并不大。因此,采用多元线性回归拟合即可获得理想的内摩擦角数据,而黏聚力c对各项物理指标相对较敏感,本节对其作线性和非线性的回归对比。
3.2.1内摩擦角φ的拟合模型
根据公式(1)建立本文研究数据的多元线性模型,内摩擦角φ与自变量ω、ρs、e间的线性关系可拟合如下:
φ=-0.27ω+15.396ρs+11.00e-3.43
(6)
公式(6)中:ω为岩土体含水率,%;ρs为岩土体干密度,g·cm-3;e为孔隙比。经试算,调整后可决系数R2=0.842,说明预测曲线基本与样本数据趋势贴近。拟合数据趋势与原样本数据对比如图4。
根据图4可知,拟合模型曲线基本代表了数据的增减趋势,并且消除了部分异常数据的影响。在已知上述物理指标的前提下可基本预测内摩擦角。

图4 内摩擦角(φ)拟合对比
3.2.2黏聚力c的拟合模型
分析原始试验数据可知,黏聚力c值随自变量的变化起伏较大,首先采用多元线性回归拟合预测模型,方法同前文所述,最终得线性方程如下:
c=-1.49ω-100.74ρs-176.20e+312.55
(7)
公式(7)中:各参数及量纲同公式(6)中规定,调整后可决系数R2=0.677,说明多元线性回归模型虽一定程度上与样本值分布趋势相关联,但拟合程度有限,并且在某些变幅较大处不能体现差别。因此,线性模型有一定局限性。黏聚力c拟合对比如图5所示。
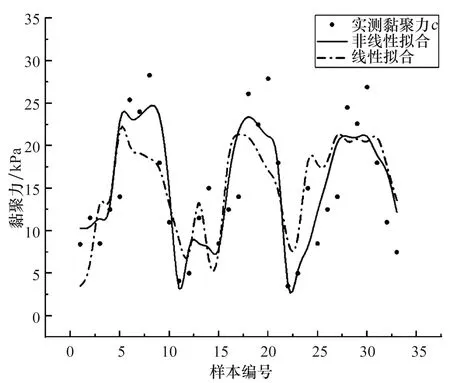
图5 黏聚力c拟合对比
采用非线性拟合时,需给定模型的基本方程。通过分析单个自变量与c的分布关系发现,3个自变量与c均呈多项式关系,ω的四次方、ρs的三次方、e的二次方对函数趋势影响较大,基于此结论并经不断尝试验算,最终确定拟合方程如下:

(8)
公式(8)中:A、B、C、D、E、F分别为各项待求系数。经不断迭代试算,最终求解得各项系数的计算结果,如表2所示。

表2 各待求系数计算结果
非线性方程的拟合结果统计于图5,调整后可决系数R2=0.795,与线性拟合结果相比,可决系数值更大,非线性拟合的计算结果与实测值更贴合,且趋势曲线可体现某些变幅较大的数值区间,相比而言拟合优势更加明显。
4 案例分析验证
为验证上述拟合预测模型,沿水泊峡水电站Ⅶ号滑坡的主滑方向剖切一条剖面进行稳定性计算,剖面分段如图6所示。根据现场资料,剖面附近钻孔钻至滑动带处时,由于钻探工艺受限,岩土体松散无法取得原状样,因此无法直接通过岩土试样获取强度参数。根据现场滑带土的赋存环境及物理指标差异,将滑带分为Ⅰ、Ⅱ两段,计算稳定性时根据各区段滑带土的物理特性分别赋值,具体参数见表3。

图6 剖面分段
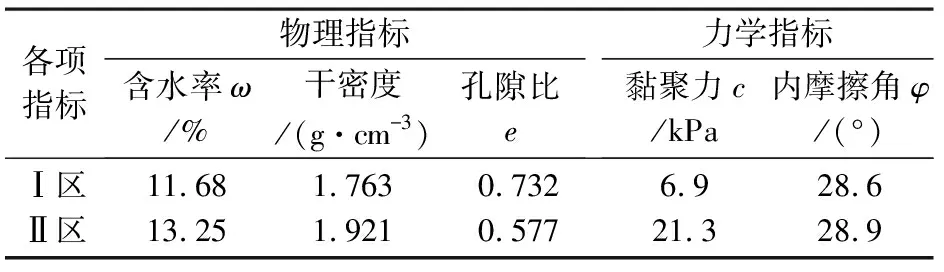
表3 剖面力学指标预测
利用前文建立的预测模型分别计算黏聚力c值和内摩擦角φ值,计算结果见表3。
根据图6所示剖面建立剖面稳定性计算模型,滑带土强度参数按表3中的计算结果分段赋予。本次分析采用Geo-Studio软件分析计算,在建立计算模型时进行了必要的简化,稳定性计算模型如图7所示。根据滑坡发育特征,在指定滑面后采用不平衡推力传递系数法计算滑坡稳定性。根据现场调查,天然状态下滑坡处于稳定状态,地震工况下滑坡发生变形,但未发生滑塌。本节只研究天然与地震两种工况,地震工况下添加“5·12”地震加速度后进行计算。

图7 稳定性计算模型
稳定性计算结果表明,滑带土分段赋予预测强度值后,天然工况下,滑坡稳定性系数K=1.434,处于稳定状态,与现状吻合;地震工况下,K=1.063,根据滑坡相关规范中规定,认为该稳定系数条件下,地震作用使得滑坡变形增大,但未发生滑动,滑坡处于整体变形~滑动状态。根据对Ⅶ号滑坡多年来的观测,天然工况下滑坡处于稳定状态,周边未见明显变形与破坏。而在“5·12”地震期间,滑坡上下游侧及后缘局部出现明显变形,并形成锯齿状拉裂缝,但整体并未滑动。综上,利用本文预测模型获得滑带土的强度参数,并用于稳定性计算,其结果与实际情形基本吻合。
综上,利用前文所研究的预测拟合模型,通过物理指标可合理预测滑带土的强度参数,且案例验证结果与实际情形基本吻合。因此,在无法直接获得岩土试样的力学参数时,本节所述滑带土的参数选取方法对同类型工程的参数选择具有参考意义。
5 结 论
(1)滑带土的物理性质与力学性质具一定关联性,在获取某滑坡大量滑带土试验参数的基础上,筛选部分物理指标作为主控因子,将力学参数作为目标参数,采用数理统计手段可拟合出合适的回归方程,用以推测选取滑带土的力学参数。
(2)以白龙江水泊峡水电站Ⅶ号滑坡为研究对象,在获取大量滑带土试验数据的基础上,将物理指标ω、ρs及e作为自变量,采用多元线性回归拟合内摩擦角φ的预测方程;分别采用多元线性回归和非线性回归建立黏聚力c的预测模型,经对比分析,非线性拟合的计算结果更贴合实测数据。
(3)沿Ⅶ号滑坡主滑方向剖切计算剖面,根据滑带土的物理指标与预测模型计算力学参数,计算得Ⅰ区滑带土c值为6.9 kPa,φ值为21.3°;Ⅱ区滑带土c值为28.6 kPa,φ值为28.9°。稳定性计算结果表明:天然工况下K=1.434,处于稳定状态;地震工况下,K=1.063,处于整体变形~滑动状态。计算结果基本与实际情形吻合。

