数学教学设计与实施课程的课程思政架构与实践

聂淑媛

(洛阳师范学院 数学科学学院， 河南 洛阳 471934)

自2016年全国高校思想政治工作会议提出“课程思政应与思政课程同向同行”的协同育人机制后， 高等院校即开展了轰轰烈烈的课程思政教育教学研究， 内容几乎涵盖了所有专业及其具体课程[1-3]. 相比之下， 中学的课程思政研究较为单薄、 零散， 就中学数学而言， 多数研究者选取一个概念、 一节实际课堂教学、 部分教材或教学内容进行思政设计[4-6]， 系统规划理论和实践相结合的中学数学大思政研究还相对欠缺.

数学教学设计与实施是学科教学(数学)方向教育硕士、 数学课程与教学论硕士研究生的学位必修课程， 其核心内容是将数学、 教育学和心理学等多门学科的基础理论与中学教学实践活动密切结合、 深度交融， 全方位提升职前数学教师的师范技能和教学实战能力， 以培养既深刻理解掌握新课程教育教学理念， 又切实具备新课改实施和研究能力的学者型中学数学教师. 它是准教师踏入真实课堂、 面向中学生授课前的高度仿真实训课程， 可谓上传高等师范教育、 下达基础教育的纽带和桥梁. 因此， 该课程的思想政治教育， 肩负着即将为人师表的青年学子、 新一代中小学生共同成长的双重责任， 其思政研究具有重要的理论价值和现实意义.

1 数学教学设计与实施课程的课程思政规划架构

为充分发挥课程思政的教育导向功能， 数学教学设计与实施课程不仅明确了课程知识目标和能力目标， 而且特别设置了育人素质目标：依据中学数学的学科知识体系和具体教学内容， 培养学生严谨推理、 科学思维的思想意识和技术方法； 结合数学史料、 数学典故和数学文化， 培养学生精益求精、 大国工匠、 科学伦理等精神； 时时、 事事、 实实渗透规则立德、 典型树德、 课堂育德的师德师风建设. 在思政总目标的指引下， 课程实行全员参与、 全过程渗透、 全方位设计的三全育人模式[7]， 整体规划架构关系如图1所示.

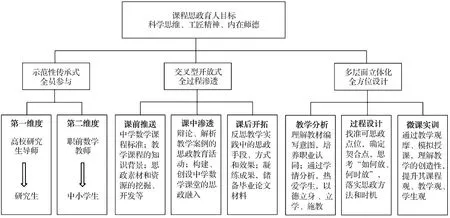
图1 数学教学设计与实施课程的课程思政规划架构图

首先， 设置两大维度开展示范性传承式的全员参与模式， 利用第一维度——从高校研究生导师、 基础课和学位课授课教师到研究生课程教学的思政示范， 引领驱动第二维度——从准数学教师、 职前数学教师到中小学生数学教学的育人实施， 通过中间枢纽研究生的传递， 在高等教育和基础教育领域营造全员参与的思政氛围.

其次， 立足于课前课中课后三维时空渗透交叉型开放式的全程思政活动， 围绕中学数学的基本教学知识点， 课前推送义务教育数学课程标准和高中数学课程标准， 深度解析其育人要求和引领价值[8]； 师生共同搜集梳理学科知识背景、 概念发展历程、 数学史与数学文化等， 挖掘思政素材. 课堂教学重点研讨、 辩论教学案例的设计模式， 依托数学知识所蕴含的哲学原理、 辩证思想、 数学美、 人文精神和理性思维等， 通过同课异构、 案例教学、 项目教学等形式， 不仅对比、 评述、 讨论教学设计中已给定的思政教育内容， 而且创新思维， 开发更新颖、 更高效的思政活动. 课后进一步反思教学实践、 拓展思政成效、 凝练成果， 为教学技能比赛、 课题申报、 毕业论文写作储备第一手材料.

再次， 实行多层面立体化的全方位思政行动方案， 对于教材和教学内容分析模块， 剖析理解教材编写意图， 以培养教育信念， 获取职业认同感； 通过对学生数学基础、 认知特点、 思维困难等学情状况的分析， 加深教师热爱学生、 理解学生的共鸣心理， 树立以德立身、 以德立学、 以德施教的师德典范. 对于教学设计的核心模块——教学过程， 关键在于根据课例的知识、 结构、 思想等特征， 找准可思政的点位， 尤其是重点章节， 认真思考思政元素和数学知识的契合点， 精心设计“如何放、 何时放”， 科学落实思政教育的方法和时机[9]. 对于教学设计的实践模块——微课实训， 通过教学观摩、 演示和模拟授课等， 引领研究生理解教学是创造性劳动和创新性思维， 不断提升其课程观、 教学观、 学生观.

2 中学数学课程思政的实践策略与案例分析

根据中学数学知识的内容分布和课堂的教学形式， 新授课是其最常见的课型， 具体又细分为概念课和命题课. 针对这两类课型的实际特点， 灵活采取课例分析法和案例教学法等多元化教学策略， 精心设计、 巧妙构思， 切实融入思政教育活动.

2.1 追根溯源、 探寻本质， 通过概念教学培养学生追求真理、 献身科学的奋斗精神和浓厚的教育情怀

数学概念反映现实世界数量关系和空间形式的本质特征， 最常用的两种学习方式是概念形成和概念同化， 其关键都在于厘清概念内涵(质的特征)和外延(量的范围)， 故立足数学史视角追溯概念的来龙去脉， 可谓探寻概念本质的最佳途径. 同时， 经过曲折、 漫长的发展历程演变形成的数学概念， 既是古往今来数学家艰苦卓越、 不懈努力的结果， 也是数学思想方法和社会文化底蕴实质性联合的科学成果， 这正是激励学生严肃思考、 潜心钻研、 勇攀科学高峰的思政资源[10]. 因此， 在探究中学数学概念课应如何设计时， 课程组选取高中数学人教版A版教材第3章“3.1.1函数的概念”这一典型课例， 以教学内容分析、 教学过程设计、 教学反思和凝练提升三个层面为切入点， 深度解析概念发展史， 密切关联思想政治教育， 具体安排和思路见表1.

根据表1可知， 厘清概念本质是概念课教学的重中之重， 为此， 教师必须非常清晰概念的诞生背景、 发展历程和形成缘由. 比如， “数系的扩充和复数的概念”是中学阶段最后一次扩充数集， 如果教师不了解数系扩充源于客观生活生产和学科内在发展两个层面， 不能领悟其中所蕴含的数学符号发展史和数集的封闭性运算， 不仅无法引领学生从系统的视角深度思考数系扩充的实质， 更无法恰如其分地在教学中穿插“第一次数学危机”“高斯、 卡尔丹等数学家的故事”“数学美”等教育意义显著的思政材料. 因此， 追溯概念渊源是教师提升课程思政素养和育人能力的契机.

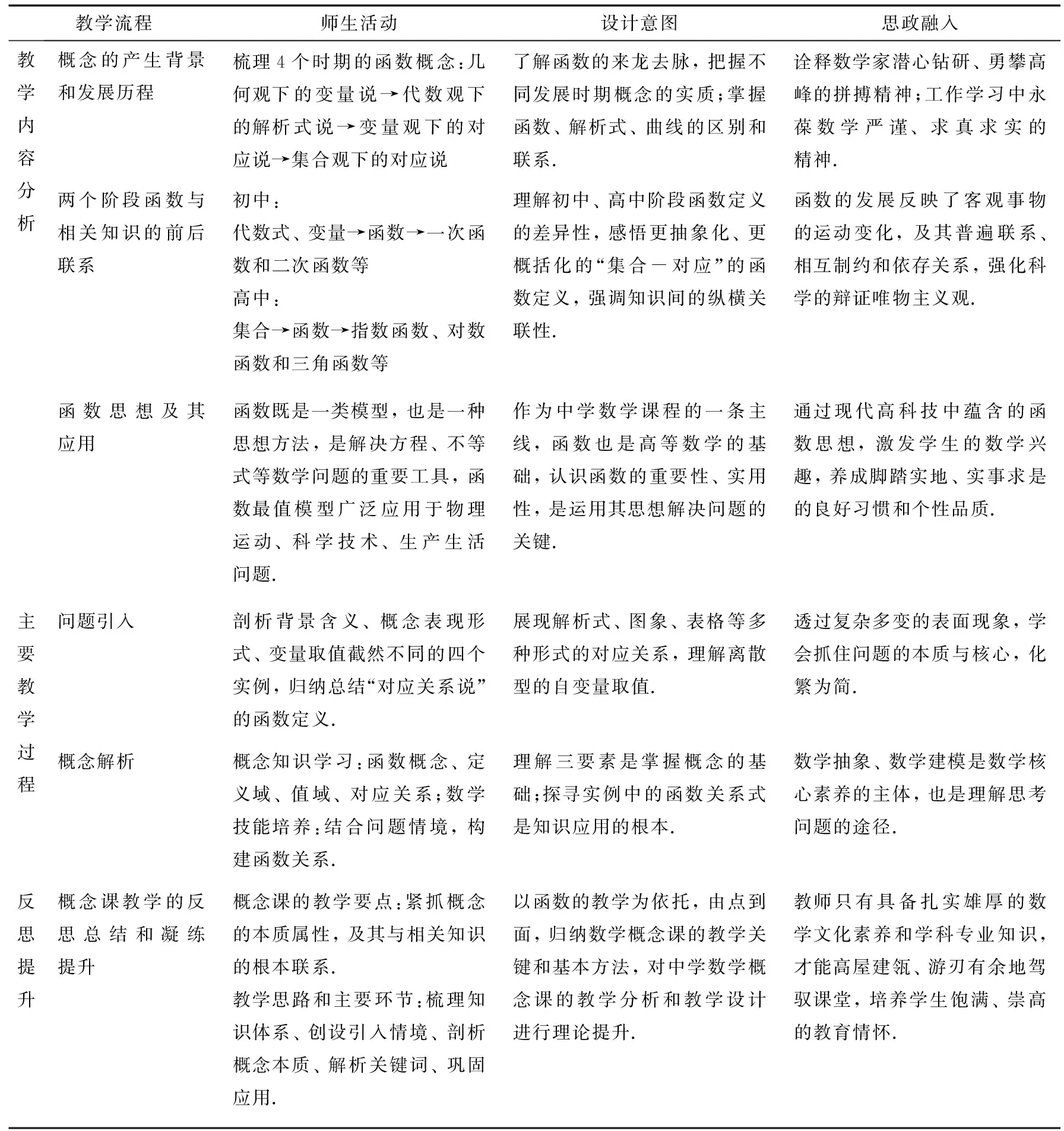
表1 中学数学概念课的教学分析和设计反思表

2.2 从探究生成到语言描述， 层层解析数学命题中的理性思维和哲学观念， 培养学生的优良品质和辩证观

概念是数学最基本的知识单元， 将其按一定规则联结组合就形成了命题. 数学命题表达一个完整的数学思想， 通常以定理、 公式、 法则的形式运用于数学判断. 数学命题的教与学不仅是培养学生学科核心素养、 发展思维能力和创新意识的一线实践活动， 也始终是中学数学教学改革的热点话题. 因此， 对于数学命题课的教学设计研究， 课程组采用全国教育专业学位研究生教育指导委员会大力倡导的案例教学法， 依托河南师范大学侯学萍教授的入库案例《落实数学核心素养的课堂教学设计旅程——以“函数单调性与导数”为例》， 全方位探究数学命题的德融课堂教学模式， 其设计思路和主要教学环节如下.

2.2.1 案例推送与任务布置

课前通过网络平台发布教学案例及使用说明书， 引导学生了解案例教学法； 查阅“函数单调性与导数”的教材和课程标准要求， 自行设计本节课的教学流程； 研读教学案例， 尝试理解Z老师三轮设计的改进和意义.

设计意图：通过课标和教材掌握中学数学课例内容， 感悟案例中多次修订教学设计的价值.

思政融入：引领研究生了解新形势下的教学模式， 强化教书育人的责任感和使命感.

2.2.2 案例剖析与观点辨析

师生经过简短对话和交流辨析， 首先提出分组讨论提纲：①结合案例中“函数单调性与导数”的教学设计， 谈谈中学数学命题课需要高度重视的关键点是什么， Z老师是如何逐步提升改进突破教学关键点的. ②在三轮教学中， Z老师如何常态化落实数学核心素养、 融入课程思政教育？这对数学命题课的教学有何启发意义？③你认为， 案例中Z老师对教学设计进行的三轮修订中最大的转变是什么？这说明了什么问题？

各小组经过组内成员的讨论交流、 梳理归纳， 组间代表的观点碰撞、 思想交融， 以及教师的穿插点拨， 逐步明晰了相关问题的核心观点. 第一， 中学数学命题课的关键环节是探究和形成结论. 对Z老师的三轮教学设计进行纵向和横向对比， 可以发现， 三轮设计都非常注重精心选取问题情境， 引发认知冲突， 为后续教学铺垫基础； 教学重心显然都在于探究、 生成和描述结论. 教学以学生已经掌握的函数图象为起点， 充分利用现代信息技术手段， 从最初的表演图像， 到利用GGB动态演示， 再到实物工具牙签的运用， 目的指向明确——探究函数单调性和导数的关系. 因此， 这类新授课的关键就是探究总结数学命题， 带领学生经历观察、 猜想、 发现、 归纳、 总结， 不仅培养其“四基”“四能”， 落实学科核心素养， 而且在这个过程中， 教师要有意识地引导学生把建构知识、 用数学语言科学描述命题的思想方法内化成自身的行为习惯， 形成优良的个性品质[11]， 这也是不容忽视的思政育人点. 第二， 中学数学命题课的思政挖掘是命题蕴含的哲理与思维方式. 比如， 函数的单调性启示我们， 人生起伏不定， 高潮和低谷始终相伴而行， 要学会用乐观积极、 辩证发展的眼光对待生活； 再如， 笔者的入库案例《在比较中发展 在评析中生成——以“二项式定理”为例》， 由格言警句“积跬步以致千里， 积怠惰以致深渊”开启教学导入， 且首尾呼应， 不仅贯彻了严格自律的生活态度和坚持不懈的行为品质， 而且培养了学生数学抽象、 数学建模的创新能力和思维理念. 第三， 教育教学改革的前提和基础是教师教育理念的转变. 限于文章篇幅， 此处不再详细分析三轮教学设计的具体改变及其优缺点， 旨在强调一个主题——正是教师教育理念的转变， 指引着教学设计的根本性变革. 案例中Z老师从第一轮“着眼于教设计学”， 到第二轮“着眼于学设计教”， 再到第三轮“从学到悟”， 不仅是讲授顺序的调整和课堂结构的优化， 更是对“教师主导、 学生主体”“自主探究”等新课改精神的落实. 由此可提醒研究生， 对于新时代的课程思政教育， 一线中学数学教师只有大胆解放思想， 积极转变观念， 才能有效拓宽思政资源， 高效实施思政活动.

研讨启示：由具体课例的教学设计及改进修订， 扩展到数学命题课的教学研磨； 由实际教学中的思政育人点， 升华到中学数学课程思政的教学策略； 注重教学案例的内容剖析， 更强调案例中教育教学思想的凝练及其对职前准数学教师的启发.

2.2.3 案例反思与延展应用

依托案例对实际课例三轮教学设计的展示解读、 对比评析， 反思中学数学教师的专业发展途径， 深度思考如何开展基于中学数学教学设计的教改课题研究， 并凝练成果， 将其灵活运用到教育教学研究论文和学位论文中. 思政融入：学以致用， 触发对自身专业成长问题的积极探究， 引领职业规划.

需要强调的是， 无论是概念课， 还是命题课， 其思政切入点都不是单一维度、 固定不变的， 需要结合教学内容， 合理选取思政视角. 比如， 上述函数概念的教学， 不仅培养学生的数学思维， 也包含着联系、 运动、 变化等辩证唯物主义观； 定积分、 数列极限等概念中的“无限逼近”“以直代取”“量变到质变”“有限到无限”等思想， 都蕴含着丰富的马克思主义矛盾观. 同时， 很多数学定理交融的数学史趣话， 也传递着拼搏奋斗的励志精神， 如勾股定理的300多种证明方法、 高斯关于等差数列求和的典故等. 此外， 对于应用综合课或复习课， 可以通过社会热点话题、 国家最新前沿成果创设问题情境， 塑造家国情怀. 比如， 关于二次函数的应用， 可借助国庆阅兵典礼上的炮弹和火箭等， 适时展现我国强大的科技、 军事实力， 树立社会主义道路的自信心等. 在梳理知识时， 教师要善于提炼数学美和数学思想方法， 以提升学生的科学人文素养. 如， 经典公式eiπ+1=0的和谐统一美， 素数的简洁美及性质应用等.

3 结语

对于课程思政的开展和落实， 应该注意， 不是每堂课都要进行思政教育， 也不是每个环节都要融入思政教育. 课程思政不是要把专业课打造成一门思想政治课， 它是一种教育教学理念， 适宜于潜移默化地“浸润”， 而不是机械地生搬硬套， 教师润物无声的“身教”， 要优于空洞的高谈阔论. 从某种意义上说， 课堂外教师认真准备、 精心搜寻、 及时发布相关课程资源， 积极建设校级、 省级优质课程； 课堂教学中注重创新教学模式， 同步提升学生的理论素养和教学实践能力， 强化课程教学对后续学业学习和将来从事教育事业的影响等， 这本身就是一种爱岗敬业、 职业道德的思政示范教育， 充满正能量和乐观精神， 富有感染力， 可高效促进学生健康阳光地专业发展， 有助于激发其饱满的教育情怀.