响应数据缺失下一般线性分位数回归模型的估计
黄婉娟,罗双华,张成毅
(1.西安工程大学 理学院,陕西 西安 710048;2.西安交通大学 经济与金融学院,陕西 西安 710049)
0 引 言
在科学研究领域,常常由于一些抽样个体不愿意提供所需信息,以及一些不可控的因素或调研人员本身原因,造成收集的数据缺失。因此,在进行统计分析时经常会遇到带有缺失数据的回归模型,尤其是生物领域和社会科学领域。针对缺失数据的研究已有很多[1-4]。在统计分析缺失数据的回归模型时,通常假设数据随机缺失,普遍使用逆概率加权的方法:ROBINS提出使用逆概率加权的方法去对协变量缺失的回归模型进行参数估计[5];WANG等提出对协变量随机缺失的广义线性模型使用局部逆概率加权方法[6];LIANG等考虑对协变量缺失的部分线性模型使用逆概率加权方法进行参数估计[7];SHEN等基于响应数据缺失下的线性回归模型,使用逆概率加权方法进行参数估计[8]。
许多加权估计方法是基于最小二乘法展开研究的。由于最小二乘法的模型误差具有重尾或偏斜分布时可能会产生不可靠的估计,所以对于数据随机缺失的回归模型,最小二乘法估计的有效性和稳健性仍面临巨大挑战。与仅依赖数据中心趋势的均值回归方法相比,KOENKER和BASSETT提出的分位数回归对异常值不太敏感,因而更稳健。于是,SHERWOOD等提出了缺失协变量的逆概率加权分位数回归模型[9];TANG等针对数据随机缺失的线性回归模型,考虑将分位数信息与最小二乘相结合以提高估计效率[10];CHEN等研究了在独立非同分布误差下观测值随机缺失的分位数回归模型的参数估计问题[11];YANG等基于分位数回归方法研究了变系数部分非线性模型的统计推断问题[12]。
尽管分位数回归有诸多的优良性能,但是利用分位数回归对实际问题进行预测时,因部分预测值可能存在尾部过于左偏或右偏的情况,而导致分位点的选取难以抉择,影响模型估计效率。因此,学者们认为它不是最小二乘的可靠替代。为了克服这个缺点,ZOU等提出了针对线性模型的复合分位数回归估计[13];随后,文献[14-15]指出不同的分位数可能承载实质上不同的信息量,适当地组合不同的分位数信息对增加估计效率至关重要,且复合分位数回归相对于经典最小二乘回归,具有抗重尾误差和高效率的优点;ZHAO等通过最佳组合分位数信息对回归模型进行参数估计,所提出的方法可应用于广泛的参数和非参数估计[14];SUN等研究了一般误差分布情况下的加权局部线性复合分位数回归估计[15];NING等运用复合分位数回归研究了协变量随机缺失的一般化线性模型[16];YANG等针对异方差变系数模型,运用加权复合分位数回归估计和变量选择进行统计研究[17];JIANG等研究了随机截尾数据下的复合分位数回归[18];KAI等基于复合分位数回归提出了半参数变系数部分线性模型的系数的有效估计量[19];TANG等研究了随机删失数据的线性模型的加权复合分位数回归估计[20];TANG等考虑了具有缺失协变量的变系数模型的复合分位数回归估计和推断,即当选择概率已知,非参数估计或参数估计时,提出未知系数函数的加权局部线性估计[21];YANG等提出了协变量随机缺失的线性模型的惩罚加权复合分位数回归估计[22];JIN等提出了缺失协变量的部分线性变系数模型的惩罚加权复合分位数回归[23]。上述研究表明,复合分位数回归方法可以显著提高估计的相对效率。
基于以上研究且受到复合分位数回归方法良好性能的启发,本文拟考虑使用逆概率加权复合分位数回归方法研究响应数据缺失的模型,主要考虑如下一般线性模型:
Y=φT(X)β+ε
(1)
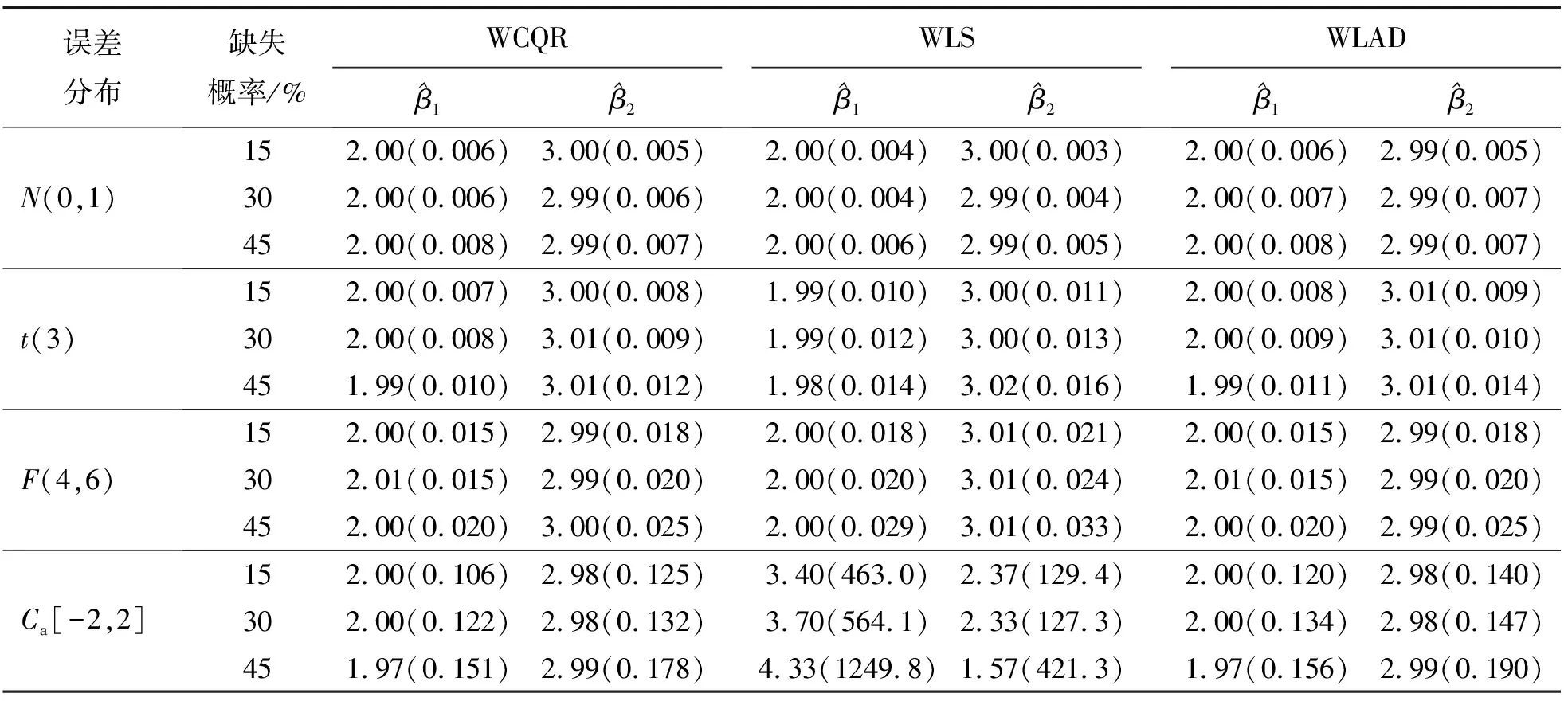
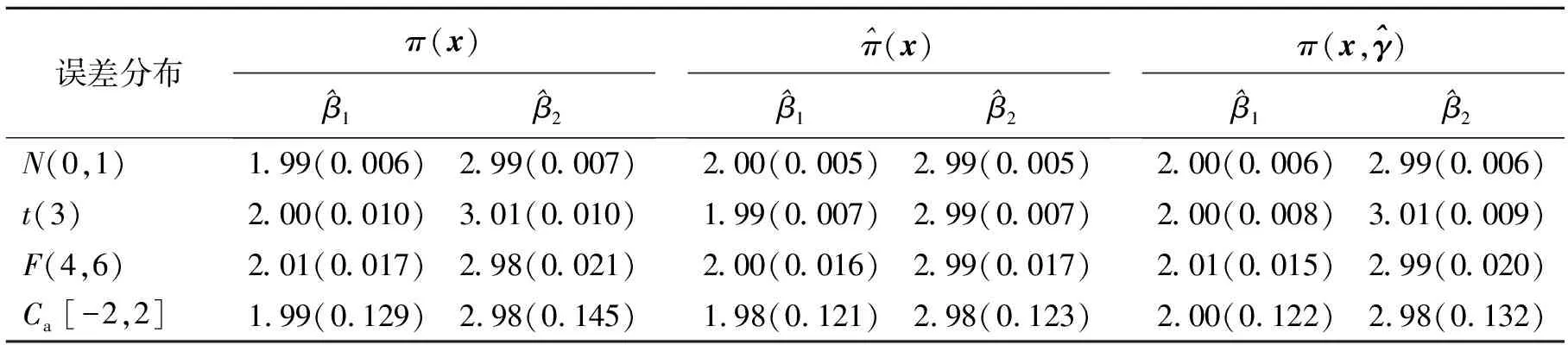
式中:Y∈R是响应变量;φ(·)为已知的p×1向量函数;β=(β1,β2,…,βp)T为p×1维未知参数向量;ε为随机误差且满足P(εi 假设{(Yi,Xi,δi),i=1,2,…,n}是模型的一组独立同分布的不完全随机样本。当δi=1时,Yi有观测值;当δi=0时,Yi缺失,随机缺失机制如下: (2) 其中,称π(x)=P(δ=1|X=x)为选择概率函数。 ρτk(Yi-ak-φT(Xi)β) 式中:ρτ(u)=u(τ-I(u<0))为分位数回归的损失函数,其中I(·)为示性函数;π(·)为选择概率函数,见式(2)。 (3) ρτk(Yi-ak-φT(Xi)β) 然而,当式(3)中X的维数太高时,非参数光滑估计π(·)将面临维数灾难, 此时使用参数模型估计π(·)更适用。令π(x)=π(x,γ),随机缺失机制被定义为 假设 π(x,γ)=(1+exp(γ0+xTγ*))-1 首先给出定理所需要的一些正则化条件: C2)矩阵D,Ω,Λ,Σ都是正定且有限的; C4)核函数K(·)是一个具有紧支撑的有界对称密度函数; 定理1假设选择概率π(x)是已知的,当条件C1)~C5)成立时,有 定理2假设选择概率π(x)≥c>0是关于x的光滑函数,当条件C1)~C5)成立时,有 式中: 定理3假设选择概率π(x,γ)含有一个未知参数γ,当条件C1)~C3)、C6)成立时,有 式中: 其中 于是 [ρτk(εi-ak-n-1/2(vk+φT(Xi)u))- ρτk(εi-ak)] 根据文献[24]中定理1的公式,∀s≠0,有 ρτ(s-y)-ρτ(s)=y(I(s<0)-τ)+ 其中 定义 ∀ε>0,有 类似文献[20],容易证明 由于 于是 其中 E[f(ak|Xi)φ(Xi)φT(Xi)] 于是 其中D=D1+D2+…+Dq。 又因为 var(Zn,k)=E[(Zn,k)2]-[E(Zn,k)]2= var(Wn)=E[(Wn)2]-[E(Wn)]2= 根据中心极限定理,于是有 根据文献[24]中引理2和文献[25],于是 其中 I(εi≤ak)]dt 注意到 其中 类似文献[26]中定理3的证明,且在条件C3)~C5)下,有 由于 因此 于是 类似定理1的证明,于是有 其中 又根据条件C6)并令Γi=(1,Xi),可得 其中π′(Xi,γ)=gradγπ(Xi,γ)。于是 其中π′(Xi,γ)=π(Xi,γ)(1-π(Xi,γ))Γi, (δi-π(Xi,γ))Λ-2+οp(1) 其中 因此 (δi-π(Xi,γ))Λ-2+οp(1) 类似于文献[9]中引理1的第二步,容易得到 类似定理1的证明,于是有 通过数值模拟验证所提出方法的有限样本性。在模拟实验中,核函数为 K(t)=0.75(1-t2)I(|t|≤1) 复合水平q=9,样本容量n=100,重复实验200次,利用交叉确认法选择最优窗宽hopt。 例1为比较WCQR(加权复合分位数回归估计), WLS(加权最小二乘回归估计)和WLAD(加权中位数回归估计)的估计效果, 现考虑如下模型: y=β1x1+β2x2+0.5ε π(x)=(1+exp(γ0+γ1x1+γ2x2))-1 式中:β1=2,β2=3;(x1,x2)是均值为0,方差为1,相关系数为0.5的二维变量。选择不同的γ=(γ0,γ1,γ2)分别为 (2,-1,0),(2,0,-2),(1,-2,-2) 实现3种缺失比分别为15%、30%、45%;且考虑4种随机误差ε分布分别为N(0,1),t(3),F(4,6),Ca[-2,2],其中Ca[·,·]为柯西分布。 表1为3种加权回归估计方法计算出参数β的均值和均方误差结果。 表 1 3种加权回归估计方法下参数β的均值和均方误差 由表1可以看出: 1)当模型误差是正态分布时,WCQR和WLS的估计效果相似,并且略好于WLAD; 2)WCQR在各种误差分布之下都表现良好,且在同一误差分布下,均方误差随缺失概率的增加而增加,而且较之WLS和WLAD,WCQR有更小的均方误差。 例2在相同缺失概率下,比较3种加权复合分位数回归估计的优越性,考虑如下模型: y=β1x1+β2x2+0.5ε π(x)=(1+exp(γ0+γ1x1+γ2x2))-1 式中:β1=2,β2=3;(x1,x2)是均值为0,方差为1,相关系数为0.5的二维变量。当γ=(γ0,γ1,γ2)=(2,0,-2),缺失比大约为30%;且考虑4种随机误差ε的分布分别为N(0,1),t(3),F(4,6),Ca[-2,2]。 表2为相同缺失概率下的3种加权复合分位数回归估计在4种误差分布下的参数估计结果。 表 2 相同缺失概率下的3种加权复合分位数回归估计 由表2可以看出: 1)在缺失概率相同的条件下,加权复合分位数回归估计方法在各种误差分布情况下的估计效果都较好; 因此,在小样本中,使用估计的权重进行加权复合分位数回归估计优于使用真实的权重进行加权复合分位数回归估计,且非参数估计略优于参数估计。 本文利用逆概率加权法给出了响应数据缺失下一般线性复合分位数回归模型的3种参数估计,即选择概率已知、选择概率未知时的非参数估计和参数估计;使用复合分位数回归方法减小了参数估计的方差,提高了估计效率,并且在一定条件下证明了所给估计量的渐近正态性。通过数值实验说明了所得估计的有效性。1 主要结果
1.1 主要方法
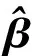
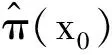
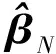

1.2 主要定理
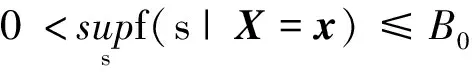
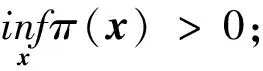
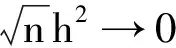
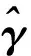

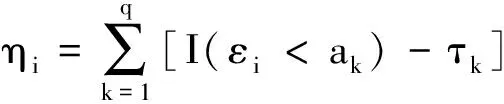
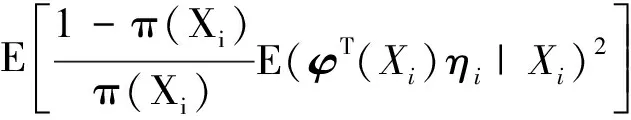
2 定理证明
2.1 定理1的证明
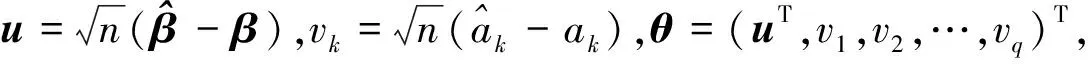

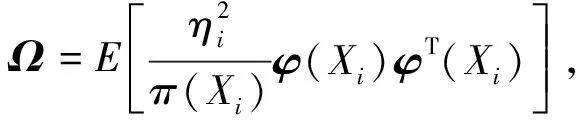
2.2 定理2的证明
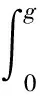
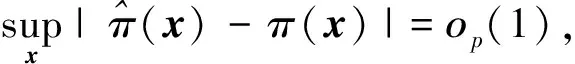
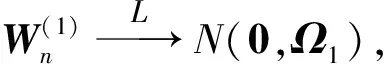
2.3 定理3的证明

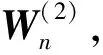
3 数值模拟
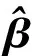
4 结 语

