多策略融合的黄金正弦布谷鸟搜索算法
刘 青,贺兴时,顾佳鑫
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
布谷鸟搜索算法(cuckoo search algorithm,CS)是YANG等基于一些布谷鸟的产卵寄生行为的群智能算法[1],具有计算速度快、稳定性高、参数少、易实现的优点。
国内外学者对该算法的改进研究,可归纳为以下几个方面:①改进算法参数:陈程等提出了动态调整概率的双重布谷鸟搜索算法(DECS)[2],相比传统布谷鸟搜索算法寻优性能有所提升,但算法步骤复杂不易理解;黄闽茗等将逐维的反向学习策略添加到动态自适应布谷鸟搜索算法中[3],但测试函数只考虑了单峰和多峰函数,算法测试效果不全面;宋庆庆等将混沌序列引入布谷鸟搜索算法,以优化鸟巢的初始位置,并在混沌序列的基础上建立布谷鸟搜索算法[4],但仅和传统的布谷鸟搜索算法进行了对比,对比算法种类较少;JABALLAH等提出了适应布谷鸟搜索算法(SACS)的方案,根据优化过程的进展动态调整控制参数[5],但算法精度有待提高。②和不同优秀算法融合:张珍珍等提出了融合正弦余弦和种群初始化策略的布谷鸟搜索算法[6];ABDEL-BASET等提出了CS-GA和GA-CA 等2种算法[7];ZHAO等将CS算法与ABC算法相结合[8];李娜等将PSO算法引入布谷鸟搜索算法[9]。不过,上述不同算法融合使改进算法复杂度变高,运算时间花费较大。③算法的应用:谢永盛等提出了一种改进算法,解决了多机器人任务分配和路径规划问题[10],但改进算法对多机器人任务分配及路径规划所需能量消耗还存在提升空间;方园园把改进的布谷鸟搜索算法应用于帮助机器人准确定位气味源[11],但固定步长的莱维飞行发现策略,得到最优解的质量有所下降。贾政方等引入离散布谷鸟算法对建筑能耗数据进行监测[12];GARG等提出了一种基于CS算法的最佳掩模生成方法,用于噪声抑制和语音信号增强[13];过文俊等采用CS算法对支持向量机进行优化,将其引入到财务数据的评估[14]。以上算法一定程度上存在通用性差,不能有效地解决各种实际问题。
可见,上述文献对于布谷鸟搜索算法的改进策略比较单一,改进算法运行时间消耗、计算精度、整体性能上还存在提升空间。本文提出一种融合多策略改进布谷鸟搜索算法(GSACS),通过对算法参数改进并与其他优秀算法的思想结合,极大地保证改进布谷鸟搜索算法的优化性能。
1 布谷鸟搜索算法
1.1 原理及相关公式
布谷鸟无固定配偶且不会筑巢孵化卵,而是在各种雀形目鸟类的巢中产卵,由这些鸟孵化后代。如果被其他鸟类发现巢穴内不是自己的后代,它们会丢弃这些鸟蛋或者重新搭建新的巢穴。同时,布谷鸟善于模仿其他鸟类的习性,以保护自己及后代不被其他鸟类发现。2009年,文献[1]基于布谷鸟的产卵寄生行为,提出了3种理想化的规则。
1)每个布谷鸟在特定的时间产了一枚蛋,并转储在一个随机选择的巢。
2)提供高品质蛋的鸟巢将孵化下一代雏鸟。
3)自然界中其他鸟类的巢穴是有限的,其他鸟类发现不是自己后代的概率为Pa(1≥Pa≥0)。在被发现后,其他鸟类将舍弃巢穴或者丢弃鸟蛋。
根据上述3种理想化规划建立布谷鸟搜索算法,更新公式如下。
1)全局位置更新[15]
(1)

(2)
式中:μ和ν服从标准正态分布,β=1.5,
(3)
α=α0(Xti-Xb)
(4)
式中:α0=0.01;Xb表示当前最优解。
根据式(1)~(4),全局搜索公式可以表示为
(5)
2)局部位置更新公式
该阶段为偏好随机游走阶段,计算公式为
(6)
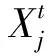
1.2 布谷鸟算法实现流程
1)布谷鸟算法各参数值设置并初始化,其中鸟巢个数为m,最大迭代次数为N。
2)计算每个鸟巢的适应度值,找出所对应适应度最优的位置,即当前最优解。
3)保留上次迭代所产生的最优位置,对剩下m-1个位置的鸟巢按照莱维飞行进行位置更新并计算适应度值。
5)按照布谷鸟巢卵发现的概率,对当前位置的布谷鸟蛋进行一轮“发现”。被发现的鸟巢则抛弃,并按照莱维飞行产生新解。
6)在新解中找出适应度最优的解并与当前最优解进行比较,有更优则替换。
7)判断算法是否达到最大迭代次数N。若达到,输出当前最优解;否则转2)。
2 改进布谷鸟搜索算法
2.1 拉丁超立方体采样初始化种群
经典的布谷鸟搜索算法一般以随机方式产生初始化种群的位置,但这种采样方法可能导致种群内个体分布不均匀,故采取拉丁超立方体抽样方法[17]产生初始种群。拉丁超立方抽样是基于空间填充技术,即在设计变量空间内的样本点在每一维上的投影都是均匀分布的。根据拉丁超立方体采样方法的初始种群位置可以保证整个空间填充和采样的非重叠,并且可以使种群分布均匀[18],同时可以在少量样本点的情况下更加充分地探索整个设计变量空间。种群初始化的具体步骤如下:
1)确定布谷鸟搜索算法种群规模N和维数D;
2)确定变量x的区间为[Ub,Lb],其中Lb和Ub分别是变量的下界和上界;
3)将变量x的区间[Ub,Lb]划分为N个相等的子区间;
4)在每一维各个子区间中随机选取一个点;
食管癌 吞咽食物有迟缓、滞留或轻微哽噎感,可自行消退,数日后又可出现,反复发作,逐渐加重。或在吞咽时,总感觉胸骨有定位疼痛。平时感觉食管内有异物且与进食无关,持续存在,喝水及咽食物均不能使之消失。
5)将抽取的每一维的点组合形成布谷鸟搜索的初始种群。
2.2 发现概率改进
发现概率保证了将最优解带到下一代以构造新的解的概率,同时发现概率用于均衡随机搜索和局部搜索之间的关系[19]。基本的布谷鸟搜索算法采用固定发现概率Pa=0.25。Pa为定值时,不能根据解的好坏进行动态调整。本文采取发现概率Pa的动态调整机制,Pa随着迭代次数增长动态变化。由于双曲正切函数具有良好的性能[20],故将双曲正切函数引入到发现概率中,对其进行动态调整。改进的发现概率公式为
Pa=tanh(0.75log(exp(-T/t)+
exp(T/t)))-0.25
(7)
发现概率随着迭代次数变化如图1所示。
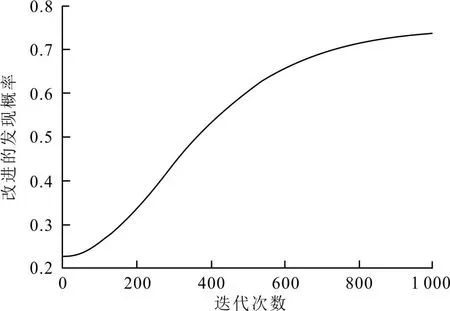
图1 改进的发现概率变化曲线
2.3 局部搜索公式改进
2017年,TANYILDIZI提出黄金正弦优化算法(golden sine algorithm,Golden-SA)[21]。由于该算法在收敛速度、求解精度方面表现优秀,被广泛应用并结合到不同的算法中。本文将黄金正弦优化算法结合到局部搜索的偏好游走公式中,即在每次算法迭代的后期对更新位置进行黄金正弦操作;并将黄金分割数添加到位置更新公式中,使搜索范围更加精准,同时有效地克服局部最优。算法中的参数r1和r2用于均衡位置迭代更新的距离和方向,合理地指引布谷鸟个体趋向于更好的个体,使布谷鸟之间的信息互通更有效。改进后的偏好游走位置更新公式为
(8)

3 仿真实验
3.1 仿真实验设计
选取适当的测试函数,通过将本文方法与布谷鸟搜索算法(CS)、自适应布谷鸟搜索算法(ASCSA)、蝙蝠算法(BAT)及萤火虫算法(FPA)进行对比,可以全面有效地测试GSACS算法的优化性能。
选取6个基准测试函数,在Matlab上进行仿真实验。其中f1(x)为Ackley函数,可有效检测算法的全局收敛速度;f2(x)是Rastrign函数,用于检测算法在求解规律中的实用性;f3(x)是Griewank函数,是检测算法跳出局部最优性能的;f4(x)为Sum Squares函数,可以检测算法的收敛性,但比Ackley函数更平滑;f5(x)为Schwefels 2.2函数,是连续的、平滑多峰函数,该函数有大量局部极值区域;f6(x)为Goldstein&Price函数,是常见的多模态基准测试函数,有多个局部极小值。6种测试函数如表1所示。

表 1 测试函数
实验环境如下:处理器为AMD Ryzen 55500U with Radeon Graphics 2.10 GHzb; 系统版本为Windows 10家庭中文版;运行内存为16.0 GiB; 操作系统为64位操作系统, 基于x64的处理器;编程环境为MatlabR2020b。
CS算法、ASCSA、BAT算法、FPA算法种群数目为25,迭代次数1 000次,各算法的其他参数如表2所示。

表 2 算法参数设置
3.2 实验结果及分析
算法的收敛曲线直观地显示了算法的收敛速度和收敛精度。图2是上述5种算法在6个测试函数上的适应度值对比图。
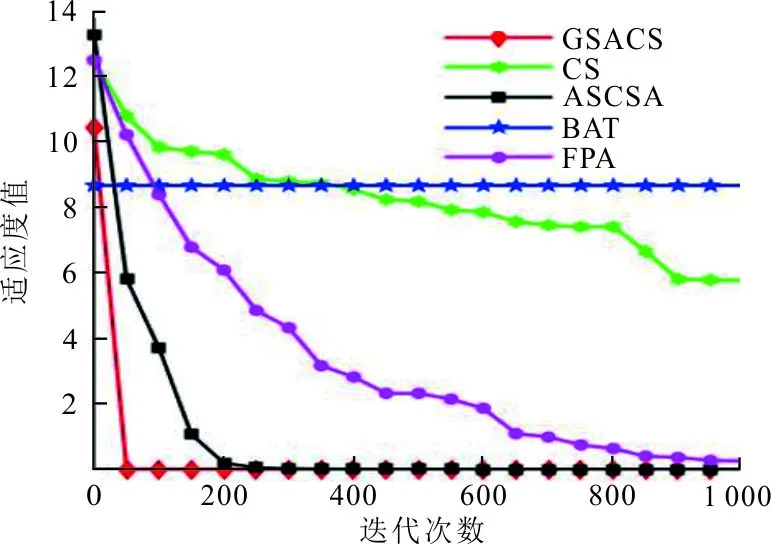
(a)Ackley函数
从图2(a)可以看出,GSACS的全局收敛速度比其他同类算法更快;图2(b)验证了改进算法的适应性能优于其他4种算法;图2(c)用的测试函数显示了算法跳出局部搜索的能力,从收敛曲线可以看出GSACS算法能有效的跳出局部搜索;图2(d)为测试收敛性能的函数,展示不同算法的收敛性能; 图2(e)、(f)为多模态测试函数,显示出GSACS算法跳出多个局部搜索范围的能力。
比较算法求解精度,用5种算法分别以50维和100维对每个测试函数独立分析,记录其标准差、平均值、最大值、最小值,结果如表3~8所示。
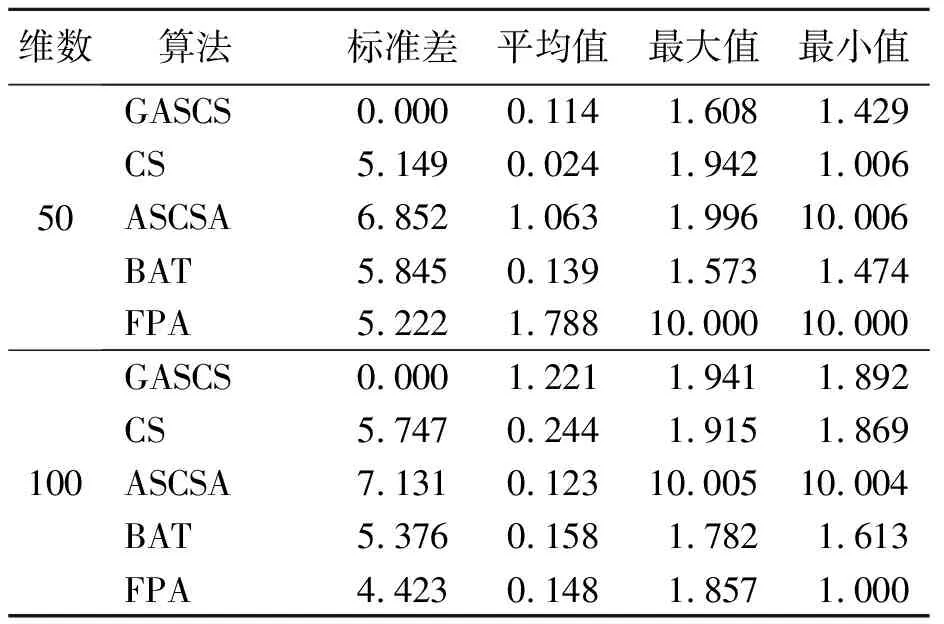
表 3 Ackley函数仿真结果
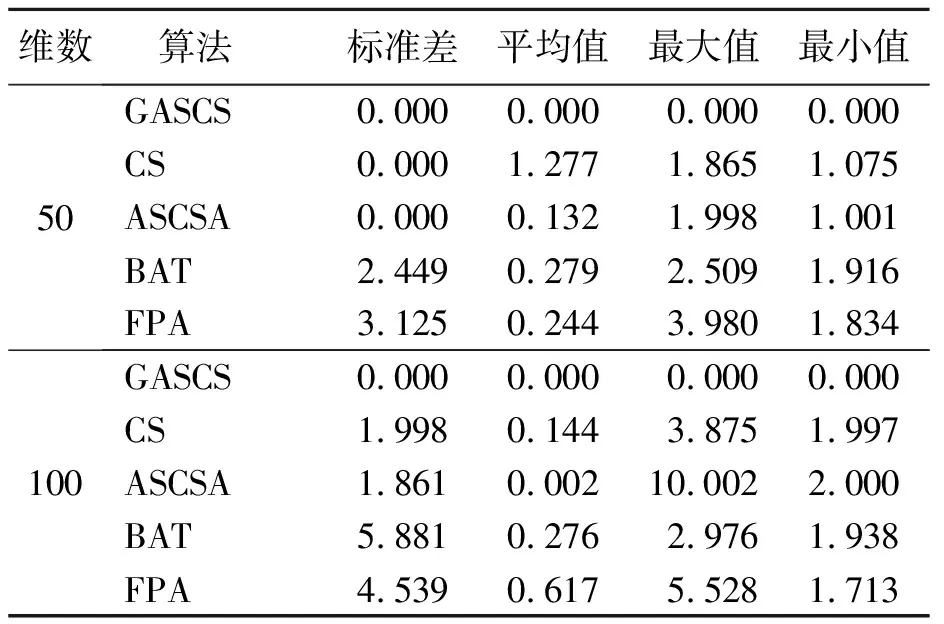
表 4 Rastrign函数仿真结果
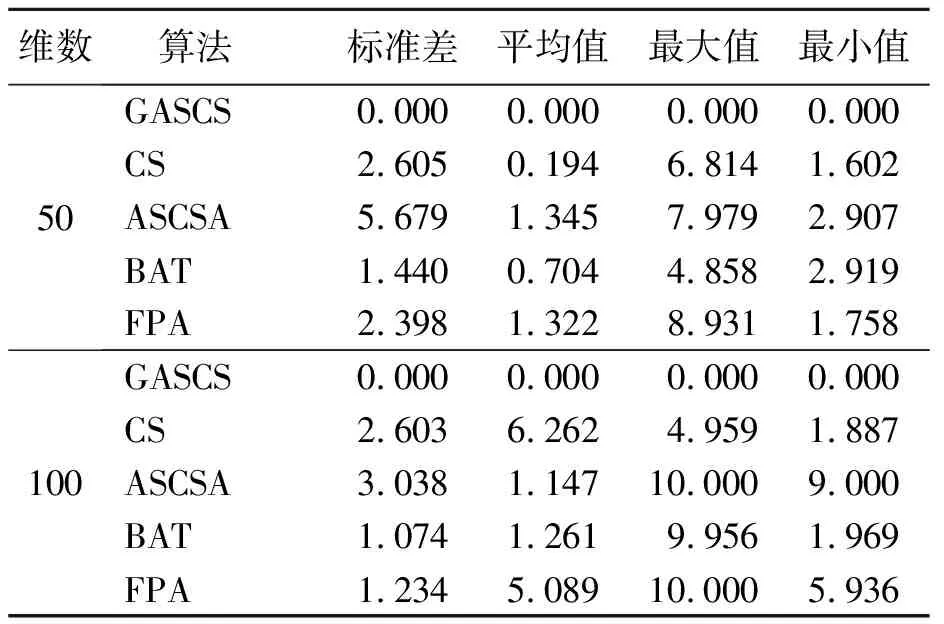
表 5 Griewank函数仿真结果
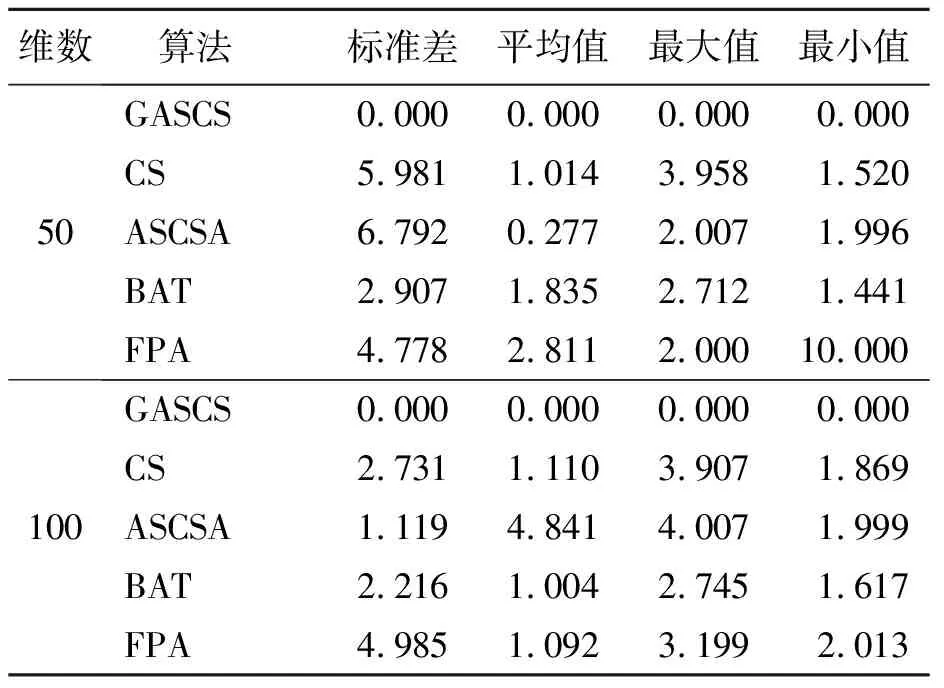
表 6 Sum Squares函数仿真结果
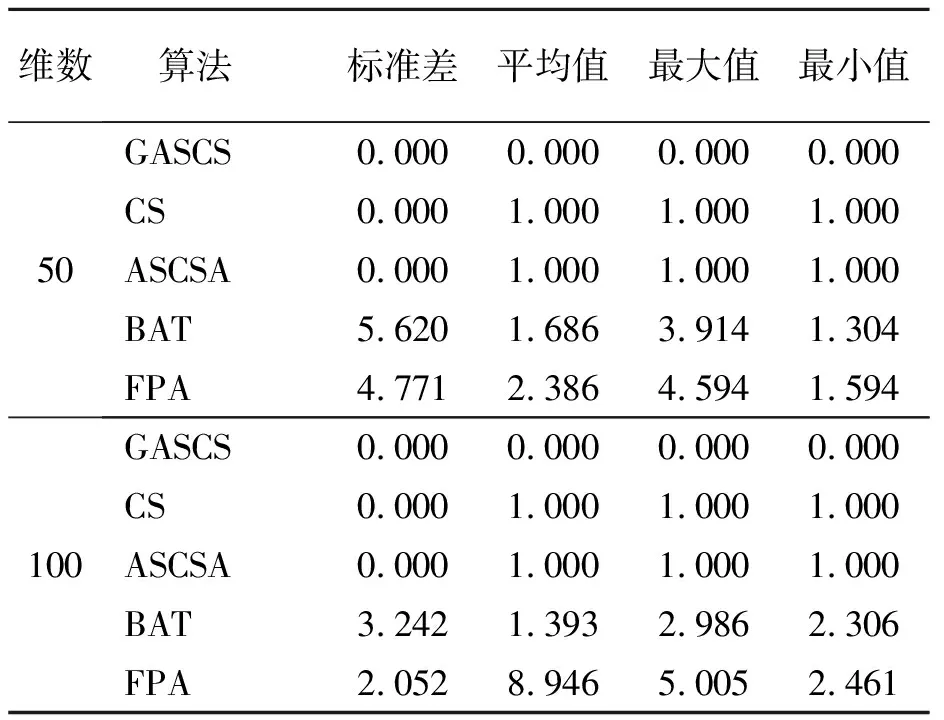
表 7 Schwefel′s Problem 2.2函数仿真结果

表 8 Goldstein&Price函数仿真结果
从表3~8可以看出,在50维、100维2种维数情况下,与其他4种算法比较,GSACS算法具有更优质的解,其他4种算法的求解精度和跳出局部搜索的能力略差于GSACS算法。
对于基准测试函数Ackley,各算法的性能表现优劣依次为:在50维下标准差评估指标的排序GASCS、CS、FPA、BAT、ASCSA。在100维下标准差评估指标的排序GSACS、FPA、BAT、CS、ASCSA。在基准测试函数Rastrign,50维情况下,GSACS、CS、ASCSA的标准差都相同;均值指标最好的为GSACS算法,最差的为BAT算法。100维情况下,各算法标准差指标的优劣排序为GASCS、ASCSA、CS、FPA、BAT。
对于不同维度Griewank函数各评估指标的表现,GSACS算法表现最好,BAT算法次之。在单模态基准测试函数Sum Squares和Schwefel′s Problem 2.2函数上,GSACS算法的求解结果标准差、最大值、平均值优于同类型算法;在多模态基准测试函数Goldstein&Price函数上,GSACS算法的求解精度和稳定性高于其他算法,GSACS的寻优能力强。
在不同维度下6个基准测试函数上的仿真结果表明,与CS算法、ASCSA算法、BAT算法、FPA算法相比,GSACS算法的性能更出色。在求解不同难度的优化问题上,该算法求解精度高、鲁棒性强。
4 结 语
针对布谷鸟搜索算法收敛速度慢且易陷入局部缺陷的问题,用拉丁超立方体初始化策略更新初始种群位置,基于双曲正切的动态发现概率,并结合黄金正弦算法的偏好随机游走位置更新算法公式。数值模拟实验结果表明,GSACS算法具有更好的性能,可以有效克服收敛速度迟缓和陷入局部最佳的缺点。同时,GSACS算法在理论上对基本的布谷鸟搜索算法进行改进和完善,并从其他高效能算法上获得启发,寻求不同算法之间的结合。GSACS算法可应用到医学、电子商务、金融等多个领域。

