基于博弈论视角的稀土矿区环境治理及监管策略研究
王秀丽, 张哲源, 李恒凯
(1.江西理工大学 经济管理学院,江西 赣州 341000; 2.江西理工大学 建筑与测绘工程学院,江西 赣州 341000)
0 引言
稀土被称作“工业维生素”和“新材料之母”,是国家的战略性资源,被广泛应用于石油化工、玻璃陶瓷、国防军事和新材料领域[1,2]。但是稀土开采往往会产生大量的浸矿废水,经过雨水的冲刷作用导致含有氨氮和重金属离子的废水进入地下水和土壤中,造成矿区环境的严重破坏[3]。
实际上,我国很早就重视稀土矿区的环境保护问题,自1989年《环境保护法》颁布以来,政府陆续出台了一系列的环境保护政策,主要包括稀土开采总量控制、调整稀土资源税以及实施矿业权设置方案制度等。但是对于稀土企业来讲,其作为理性的“经济人”,稀土企业往往消极对待环境规制[4,5]。而政府作为公众利益的代表,主动积极地调整政策以限制稀土企业的非法排污行为[6]。这种政府和稀土企业之间的动态过程与博弈行为具有内在的契合性。
我国的环境规制是由中央政府统领全局,各地方政府结合实际制定相应的规制策略并执行的过程,其实质是政府为削弱经济活动的负外部性[7]。国内外学者关于环境规制实施过程中各利益主体间的相互博弈研究较多,且主要集中在三个方面。一是研究地方政府和企业之间的博弈关系,如Presley和Lin[8]以及Xia H[9]发现当排污税较高时能有效的促进企业选择合法排污策略;曾繁伟[10]和涂国平[11]探讨了中心点位置博弈双方的演化过程。二是研究中央政府和地方政府之间的博弈关系,如潘峰[12]、潘鹤思和李英[13]分析博弈参与者之间的演化规律和演化稳定策略;游达明[14]和吴士健[15]通过研究发现,中央政府和地方政府之间的博弈走向,很大程度上取决于地方政府环境规制执行力度以及中央政府监管力度和处罚力度等。三是研究公众参与下政府和企业之间的博弈关系,如Zhang和Kahn[16]等考虑公众对政府和企业之间相互博弈的影响;王丽珂[17]、彭皓玥[18]和徐松鹤[19]分析了博弈双方对待环境污染时的理性冲突与合作。
鉴于此,本文构建地方政府和稀土企业之间的演化博弈模型,分析环境规制下博弈双方的行为策略选择,从动态博弈的角度研究了两者在动态稳定点的均衡性,并利用matlab对其进行数值仿真,并针对分析结果提出一些合理性的建议。
1 模型假设与符号说明
1.1 模型基本假设
本文以地方政府和稀土企业为研究对象,并且假设两者存在博弈行为且均为有限理性。其中,稀土企业可以选择较高治污成本的“合法开采”,将废水的排放量控制在标准范围内,而部分稀土企业为了追求利益最大化超出政府规定的标准排放废水造成环境的严重污染,此时选择较低治污成本的“非法开采”;地方政府可以选择执法频率较高的“严格监管”,可以及时发现稀土企业的“非法开采”行为,除征收稀土企业固定的达标排污费外,还需征收超出排污标准之外的罚款,而由于稀土企业产生的经济效益反映了当地政府的绩效高低,部分政府监管机构为了本地的经济发展迅速,选择较低频率的“不严格监管”,不能发现稀土企业的“非法开采”行为,但是此时造成的环境损伤由政府承担。
1.2 基本符号说明
地方政府的总收益为D,当地方政府执行“严格监管”的策略时,其执行成本为C1,对稀土企业造成的经济损失为G,当地方政府执行“不严格监管”的策略时,其支出和收益均为0,当稀土企业执行“合法开采”的策略时,其执行成本为C2,地方政府对其的奖励为R,对该地区带来的环境收益为M,当稀土企业执行“非法开采”的策略时,其额外收益为F,对该地区带来的环境损失为N,地方政府规定的污染物排放标准为S,α为稀土企业的开采活动产生的废水总量,β1,β2分别为稀土企业选择“合法开采”策略和“非法开采”策略时废水的消减量,h1为稀土企业“合法开采”时的排污量,其值为α-β1,h2为稀土企业“非法开采”时超出排放标准的排污量,其值为α-β2-S,λ1为废水排放量在标准范围每单位环境税额,λ2为废水排放量超出排放标准范围的每单位环境税额。
2 地方政府环境规制策略行为演化博弈分析
2.1 博弈双方的演化博弈模型构建
由上述假设条件,考虑地方政府和稀土企业均为有限理性,可以独立随机地选择执行某一策略,得到两者的阶段博弈支付矩阵如表1所示。

表1 地方政府与稀土企业的博弈支付矩阵
假设稀土企业选择“合法开采”策略的比例为x,则其选择“非法开采”的比例为1-x,其中0≤x≤1;地方政府选择“严格监管”的比例为y,则其选择“不严格监管”的比例为1-y,其中0≤y≤1。
则当稀土企业选择“合法开采”策略时的期望收益为:
Ex=y(R-C2-G-λ1h1)-(1-y)C2
(1)
稀土企业选择“非法开采”策略时的期望收益为:
E(1-x)=y(F-N-λ1h1-λ2h2)+(1-y)F
(2)
稀土企业的平均收益为:
=x[y(R-G-λ1h1)-C2]+
(1-x)[F-y(N+λ1h1+λ2h2)]
(3)
根据Malthusian方程,并将上述三个方程联立,可得稀土企业的演化博弈动态复制方程为:
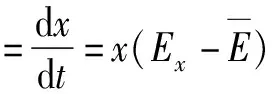
=x(1-x)[y(R+N-G+λ2h2)-C2-F]
(4)
当地方政府选择“严格监管”策略时的期望收益为:
Ey=x(D+M-R-C1+λ1h1)+
(1-x)(D-C1+λ1h1+λ2h2)
(5)
地方政府选择“不严格监管”策略时的期望收益为:
E1-y=D-N+xN
(6)
地方政府的平均收益为:
=y[(D-C1+λ1h1+λ2h2)+x(M-R-λ2h2)]+
(1-y)(D-N+xN)
(7)
根据Malthusian方程,并将上述三个方程联立,可得地方政府的演化博弈动态复制方程为:
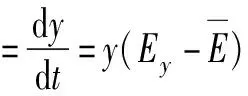
=y(1-y)[N-C1-xN+λ1h1+λ2h2+x(M-R-λ2h2)]
(8)
则该复制动态系统为:
(9)
2.2 博弈双方演化稳定性分析
在该复制动态系统中,地方政府和稀土企业均存在不同的均衡点,如从某均衡点的任意临近区域出发,其轨迹曲线最终都指向该均衡点,则该均衡点是局部渐进稳定的,不同均衡点自由组合所对应的策略即为演化稳定策略(ESS),令V1(x)=0,V2(y)=0。
则有:E1(0,0),E2(0,1),E3(1,0),E4(1,1),E5(x*,y*),其中
(10)
根据雅克比矩阵局部渐进稳定性的分析方法,对地方政府和稀土企业的演化博弈动态复制方程分别求偏导,可以求得两者在演化均衡点的稳定性并对其进行分析,该系统的雅克比矩阵如下:
(11)
其中:
(12)
则有该矩阵的行列式为:
detJ=a11·a22-a12·a21
(13)
该矩阵的迹为:
trJ=a11+a22
(14)
根据演化博弈理论可知,当均衡点的雅克比矩阵满足detJ>0且trJ<0时,该均衡点为系统中的稳定点,即存在ESS;当均衡点的雅克比矩阵满足detJ>0且trJ>0时,该均衡点为系统中的不稳定点,而当均衡点的雅克比矩阵不满足上述条件时,该均衡点为系统中的鞍点,将5个均衡点分别代入公式中,得到:
(15)
(16)
(17)
(18)
(19)
为便于分析,令
(20)
其中π1表示稀土企业选择“非法开采”策略时,地方政府选择“严格监管”策略的收益与环境损失的和值,π2表示地方政府选择“严格监管”策略时,稀土企业选择“合法开采”策略的收益与稀土企业选择“非法开采”策略的收益的差值,π3表示稀土企业选择“合法开采”时,地方政府的收益,π4恒大于0。对π1,π2,π3两两做差值:
π1-π2=C2+F+G+λ1h1-C1-R
(21)
π1-π3=N+λ2h2+R-M
(22)
π2-π3=2R+N+C1+λ2h2-G-C2-λ1h1
(23)
结合实际可知,就稀土矿区而言,其中π1-π2和π2-π3的差值无法确定其正负关系,而π1-π3的差值为正值,这是由于稀土企业选择“非法排污”策略时对环境造成的损失实际上应该是大于或等于该企业选择“合法排污”策略时对环境所带来的收益,同时对于稀土企业来讲,其本身获得的利益也小于其付出,不符合稀土企业作为“经济人”的需求,因此当π1<0时,π3<0,故根据以上分析,可以将其分为6种情形,因本文篇幅有限,以其中3种情形为例:
情形1π1>0,π2>0,π3>0
在此条件下,该系统存在2个鞍点、1个稳定点、1个不稳定点以及1个中心点(见表2),其中,E4(1,1)为演化均衡点,即稀土企业选择“合法开采”策略,地方政府选择“严格监管”策略。
情形2π1>0,π2>0,π3<0

情形3π1<0,π2>0,π3<0
在此条件下,该系统存在2个鞍点、1个稳定点、1个不稳定点以及1个中心点(见表2),其中,E1(0,0)为演化均衡点,即稀土企业选择“非法开采”策略,地方政府选择“不严格监管”策略。
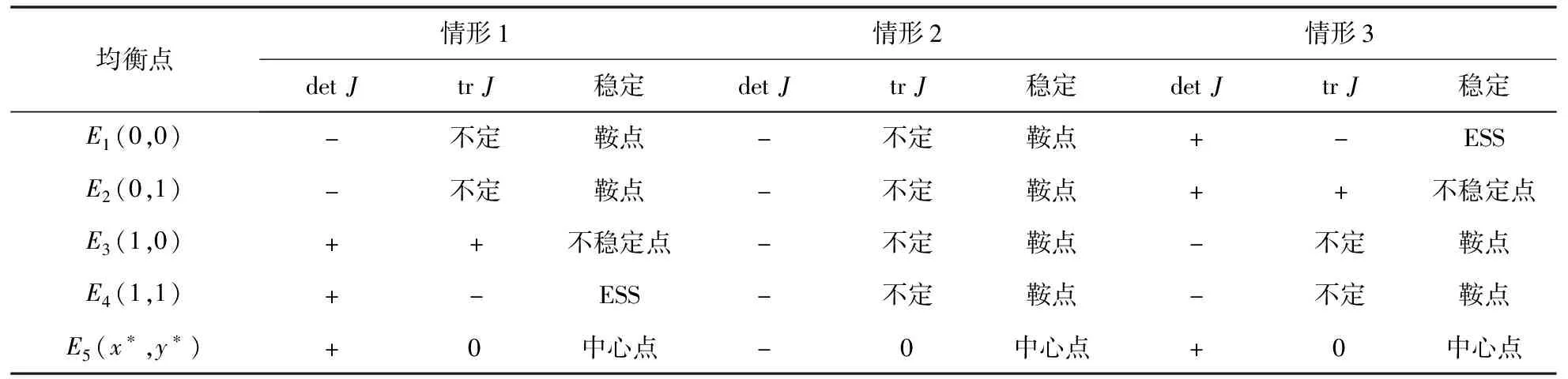
表2 局部均衡点稳定性(情形1、情形2、情形3)
3 数值仿真
为了进一步分析博弈双方在不同限制条件下的行为策略选择,本文首先在满足前文所有情形的前提下设定其参数,利用matlab对3种不同情形下的博弈双方的动态轨迹进行仿真。
根据变量定义可知,D,C1,G,C2,R,M,F,N,λ1h1,λ2h2≥0,且N≥M,λ2h2≥λ1h1,在定义范围内设定初始值,再结合情形1的限定条件,由于变量D对该系统的结果无影响,因此仅设定模型中其余9个变量的初始值分别为C1=6,G=1,C2=8,R=2,M=3,F=5,N=3,λ1h1=6,λ2h2=10,时间段t∈[0,25],其对应的系统演化如图2所示,随着时间t的增加,x和y的演化轨迹均趋于1,即E4(1,1)为博弈双方的演化稳定策略,其原因在于稀土企业选择“合法开采”策略的执行成本较低,稀土企业的财政压力小,且会受到地方政府的奖励,同时也提高了稀土企业的社会声誉,对于地方政府来说,其监督的成本处于较低水平,选择“严格监管”策略不仅不会带来财政压力,还会给政府带来良好的评价。
根据情形2的限定条件,设定模型中其他变量不变,将C1=6→10,其对应的系统演化如图3所示,随着时间t的增加,x和y的演化轨迹周期震荡,不存在稳定的均衡状态,其原因在于当地方政府的监督成本增加后,总体上博弈双方的成本、收益以及奖惩均发生变化,导致该系统很难达到稳定的状态,因而两者采取的行为策略也是不定的。
根据情形3的限定条件,设定模型中其他变量不变,将C1=6→20;其对应的系统演化如图4所示,随着时间t的增加,x和y的演化轨迹均趋于0,即E1(0,0)是博弈双方的演化稳定策略,其原因在于地方政府选择“严格监管”策略时的执行成本过高,严重制约了地方经济的发展,导致地方政府选择放弃严格监管,对于稀土企业来讲,当地方政府不严格监管时,无论稀土企业的治污成本如何,作为理性的“经济人”,为了追求自身利益的最大化,稀土企业均会选择“非法开采”策略,以降低自身的运营成本和获得额外收益。
4 结论与建议
本文以地方政府和稀土企业均存在“有限理性”为前提,运用演化博弈理论分析了两者在环境规制下的行为策略选择,得到如下结论:(1)稀土企业的治污成本、非法开采的额外收益以及政府的奖惩政策是影响其策略选择的关键因素;(2)当地方政府的监管成本和稀土企业的治污成本均为较低水平时,博弈双方的收益均大于其支出,相对应的演化稳定策略为{严格监管,合法开采}。
稀土矿区环境的治理有赖于地方政府的严格监管,为抑制稀土企业的非法开采行为,促进矿区环境的可持续性发展,基于上述分析结果,提出如下政策建议:
(1)通过财政补贴、财政转移以及加强各部门之间的合作等方式降低地方政府的监管成本;其次,为积极研发新治污技术的稀土企业提供政策支持,如税收减免、发放低息贷款等,以降低稀土企业的治污成本。
(2)地方政府应加强对矿区企业的非法开采的执行力度,对非法开采且造成严重环境危害的稀土企业,一经查明,则给予高额的罚金处罚,此外,对其开采许可证进行重新审查,严重时吊销其营业执照。
(3)建立包括居民、稀土企业、地方政府在内的环境监督体系,完善相应的法律制度,矿区周围的居民及时可以向地方政府公诉稀土企业的不治理或某些政府机构的不作为,并对公民的公诉行为进行保护并给予奖励,切实保障居民的合法权益,引导居民积极参与环境规制政策的监督。

