基于多分量电磁远探测仪的井旁裂缝特性研究

仵 杰，云 腾，胡 静

(1.西安石油大学 电子工程学院，陕西 西安 710065；2.光电油气测井与信息检测教育部重点实验室，陕西 西安 710065)

引 言

裂缝是油气储存和渗滤的重要通道。井旁裂缝的发育及分布影响着仪器探测油藏描述能力的感应成像[1]。裂缝储集具有非均质性强、各向异性明显、发育尺寸不一、填充物质多样等特点，这使得测井响应复杂，测井识别与定量评价难度很大[2]。目前主要利用阵列声波或电磁感应成像对裂缝型储层进行研究，阵列声波虽能够识别井壁较近的裂缝，但受井眼条件影响很大。电磁感应成像虽然可以比较直观、准确地识别切割井壁的裂缝，但根据获取资料很难有效地评价井旁裂缝[3-4]。

传统的测井工具和服务受限于有限的勘探深度，难以满足需求，而远探测技术对井周围地层构造及地质体的探测范围达到数米到数十米，因此可以用来探测井旁地层的内部构造。现有的远探测技术主要包括：声波远探测、电磁远探测等。声波远探测早已投入研究且基本理论日趋完善；而电磁远探测技术仅在国外研究中取得了显著的成果，在国内发展较晚，尚处于起步阶段。2015 年斯伦贝谢公司推出GeoSphere 服务，探测深度达30 m，与包括SpectraSphere 井下流体分析服务在内的整套随钻测井技术以及地表测井技术结合使用，可产生真实反映油藏结构与流体的测绘图，有利于优化井位，最大化油藏接触，改善油田开发方案。2018 年哈里伯顿公司推出的EarthStar 服务，将探测距离提高到61 m。随钻远探技术可以探测井筒周围数十米距离内的流体、油藏边界，具有随钻油藏描绘、地质导向功能。

常规地质导向中随钻电磁波测井仪器常采用轴向天线，只有一个方位的发射线圈和一个方位的接收线圈，测量不具备方位性，无边界距离探测能力，在地质边界探测等地质导向应用中受到了很大限制[5-6]。基于均匀无限大的地层假设，常规线圈系的轴线与井轴平行或重合,只能给出水平方向的一维电阻率，因此很容易低估储量，漏测储层[7]，难以清楚准确地反映裂缝的储存特性，这给该类储层的识别和综合评价带来较大困难[8]。

本文通过多分量电磁远探测仪器，基于其多分量电磁信号方向敏感性，利用其探测范围远的特点，对地层裂缝储层特征进行三维描述。通过COMSOL仿真软件建立响应模型，分析井旁裂缝的空间位置、张开度、方位角和俯仰角对电磁远探测响应特性的影响，为电磁远探测测量裂缝提供可靠的依据，对电磁远探测仪器在裂缝油气藏勘探开发中的应用具有重要的意义。

COMSOL 是一款基于有限元分析的多物理场仿真软件,可以实现各种物理电磁远探测的影响特性过程的模拟。本文利用该软件性能高效、可用于多项耦合的特点，对多分量电磁远探测仪井旁裂缝进行了模拟仿真[9]。

1 构建用于数值计算的裂缝地层测井模型

1.1 仪器和裂缝地层模型的建立

裂缝是岩石由于构造变形或物理成岩作用形成的面状体。根据天然裂缝的规模，将其分为大尺度裂缝、中尺度裂缝、小尺度裂缝和微尺度裂缝4级[10]。本文主要利用多分量电磁远探测仪器，选择大尺度裂缝进行地层裂缝储层特征的研究。

利用X/Y双线圈系结构的电磁远探测测井仪器对地层裂缝储层特征进行研究，仪器线圈布置如图1所示。在双线圈结构中发射线圈T与接收线圈R1间距为5.5 m。以实际仪器为坐标原点，发射线圈T和接收线圈R1位置分别为-3.5 m和2.0 m。发射线圈包含3个方位(Tx、Ty、Tz)，X/Y接收线圈包含2个方位(Rx、Ry)，多分量电磁远探测仪器测井可以获取XX、XY、YX、YY、ZX、ZY(6个)方向的地层内部响应信息。

图1 仪器线圈布置示意图

由于线圈尺寸和线圈间的距离相比很小，因此把发射线圈看成是振荡的磁偶极子源[11-12]，磁矩M=nTS0I，其中nT是发射线圈匝数，S0是发射线圈的面积，I是发射线圈上的交流电流。为了计算方便，将实际仪器结构参数进行等效，建立COMSOL模型等效参数(表1)。

表1 模型参数

目前，国内外使用的多分量感应测井仪器均采用单发射多接收的阵列感应设计思想，每组子阵列由3个中心共点的、相互正交的发射线圈(Tx、Ty、Tz)和与其平行的3个接收线圈(Rx、Ry、Rz)组成。三分量感应子阵列线圈系结构如图2所示，其中法向为z方向的垂直发射线圈产生垂直于井轴方向的涡流，其探测方法与传统仪器相同，主要测量地层的水平电导率；法向为x方向和y方向发射线圈产生平行于井轴方向的涡流，主要测量地层的垂直电导率,经过工程刻度组成9个分量的张量地层电导率[13-15]，本文多分量远探测仪器也是基于此设计思想，由于裂缝位于井旁的特性，接收线圈Z方向的响应特性影响意义不大，故选取X/Y方向进行仿真研究。

图2 三分量感应子阵列线圈系结构

数值计算中，首先要确定求解区域，求解域的半径大于等于趋肤深度的3倍。趋肤深度计算公式为

(1)

式中：ω是角频率，ω=2πf，rad/s；μ是地层磁导率，H/m；σ是地层电导率，S/m。本文中地层σ的值是0.01 S/m，当f=1 kHz时，求解区域为159.155 m，当f=20 kHz时，求解区域为35.588 m。裂缝的影响发生在地层，必须通过计算仪器(或裂缝)移动时的测井响应分析其影响规律。在裂缝空间位置移动的条件下，为了缩小模型尺寸，满足模型几何大小大于3倍趋肤深度的要求，需要在地层模型外围添加一层无限元域，将此区域的物理宽度设置为1 000，即实际中的地层尺寸为模型中地层尺寸的1 000倍。

图3是用于数值计算的裂缝地层测井模型，由井眼、裂缝、围岩3部分构成，裂缝垂直于围岩中，平行于仪器和井眼，井眼中有缠绕线圈的仪器棒。井眼和仪器同轴，井眼平行裂缝正中心，裂缝处于围岩中心。设置围岩为高度100 m，半径50 m的圆柱体，裂缝的长度为20 m，高度为40 m，线圈半径为0.03 m，井眼半径为0.1 m。

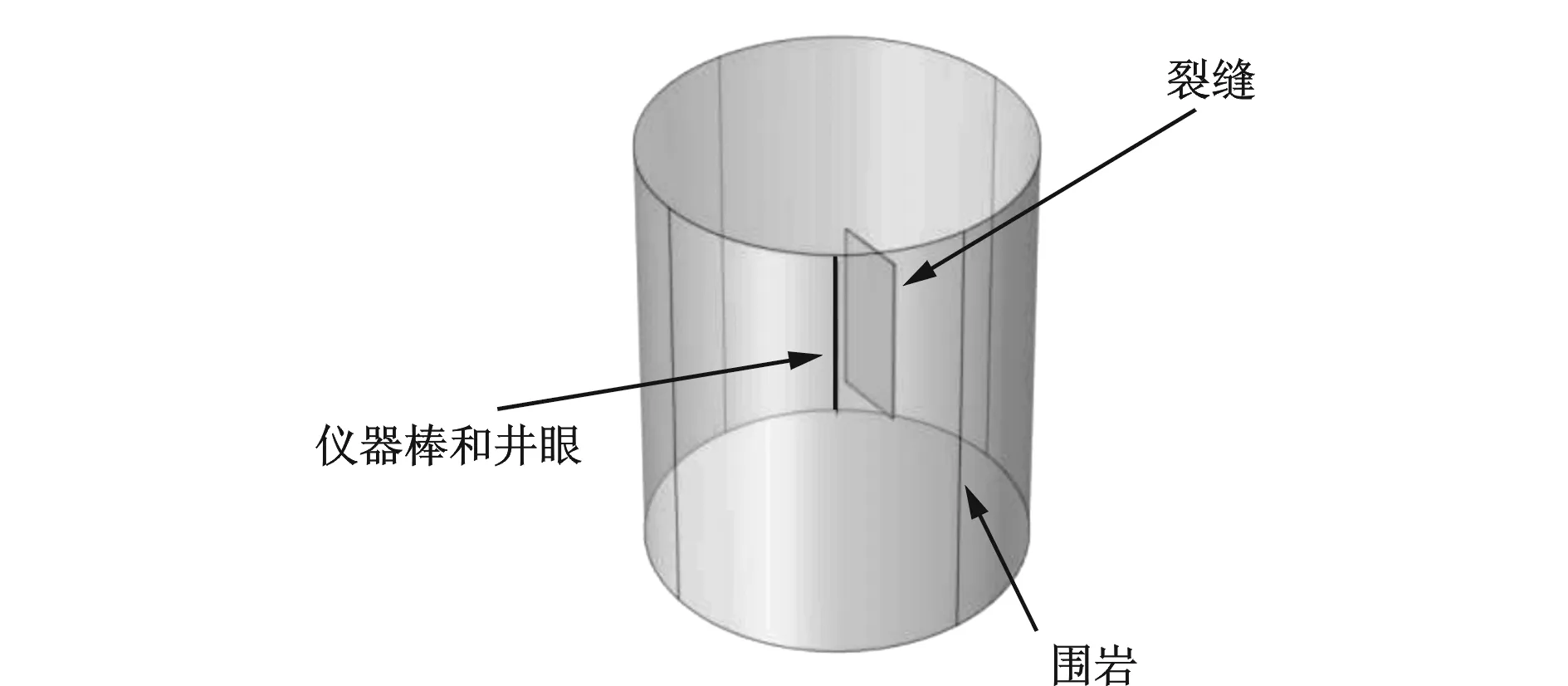
图3 垂直裂缝模型

1.2 数值计算的验证

对模型的适用性和网格剖分的合理性进行了验证。将仪器所处地层的电导率σ设置在0.01～1 S/m范围内，同时设定用于电流发射的线圈内存在1 A的电流，发射频率选择20 kHz。COMSOL计算得到的视电导率数值解和MATLAB计算得到的视电导率解析解响应数据见表2。

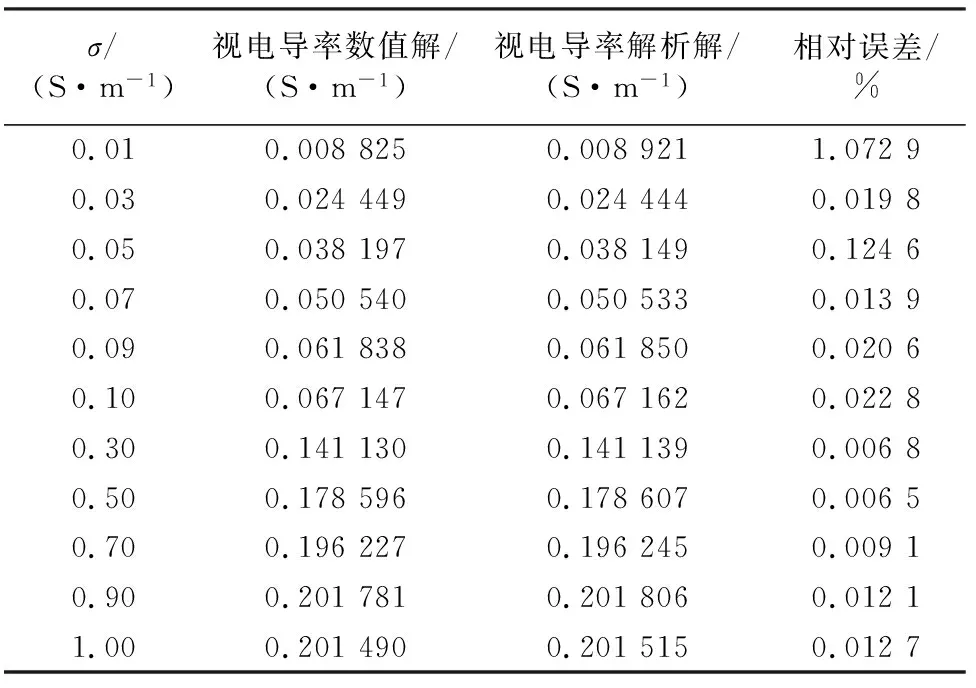
表2 均匀地层下视电导率解析解与数值解的数据对比

由表2可得：当地层电导率在0.01～1.00 S/m 范围内，仪器的相对误差均小于1.1%，符合仪器探测精度的要求，由此也证明了裂缝地层模型的适用性和网格剖分的正确性。

在实际工程中，设置频率为1 kHz时，对发射Z方向的信号测量进行了实验研究，对双线圈电磁远探测仪器进行了室内刻度响应的研究，实验结果验证了远距离收发信号的有效性，刻度响应曲线如图4所示。

在图4中，F1代表本文中的X/Y双线圈系结构，ZX和ZY代表不同方向的分量，LR为实部信号，LX为虚部信号。图中的响应曲线是在电阻为2.3 Ω的4 m长方形刻度盘中得到的，由此验证了远距离收发信号的有效性。因此，基于多分量远探测仪器对井旁裂缝研究是合理的且能够实现信号探测的。

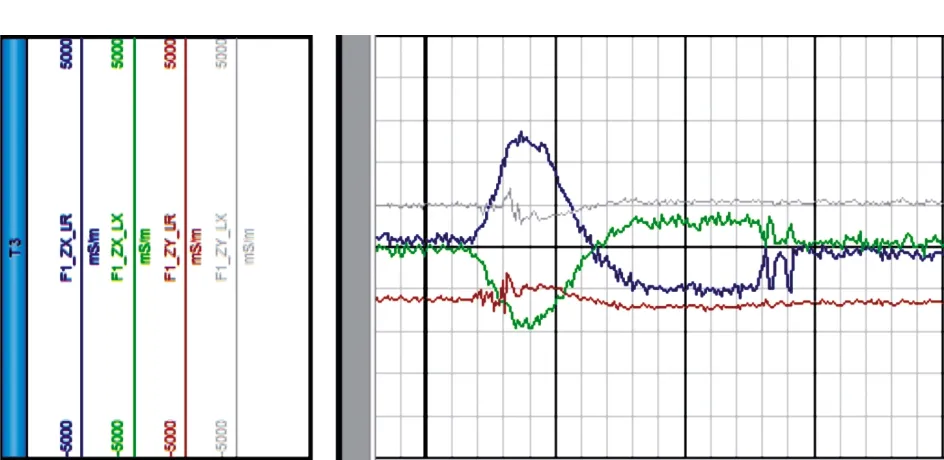
图4 双线圈电磁远探测仪器室内刻度响应曲线

2 数值模拟

本文主要研究多分量电磁远探测仪器下裂缝响应特性，影响电磁远探测测井响应敏感性的因素主要包括裂缝的空间位置、裂缝张开度、发射线圈频率、裂缝方位角和裂缝俯仰角。

数值模拟计算得到的是电压信号，本文只分析电压达到设定的50 nV阈值时分量的响应特性，该模型下，裂缝位于仪器的X轴正半轴方向，仅在XX、YY和ZX方向有有效电压信号。为了方便分析，通过电压信号计算得到它们的视电导率。本文计算不考虑井眼和侵入的影响。

2.1 垂直裂缝模型

裂缝垂直于围岩中，与仪器平行，探究裂缝在不同空间位置下，张开度和发射频率的响应特性。此模型下，主要探究裂缝在不同空间位置下，张开度和发射频率的响应特性。本文选择了2种发射频率，仪器距离裂缝12种不同的空间位置，给出了裂缝5种张开度，具体模型参数见表3。

表3 垂直裂缝模型参数

表3中Cs为围岩的电导率，Cc为裂缝的电导率，仪器棒垂直放置于围岩中心，DIST为仪器棒距离裂缝的距离，OP为裂缝的张开度。

2.1.1 裂缝空间位置和张开度的影响

为了研究裂缝空间位置和张开度的影响，选择发射线圈频率为1 kHz，按照表3中的数据，改变裂缝不同空间位置上的张开度。绘制图形如图5所示。

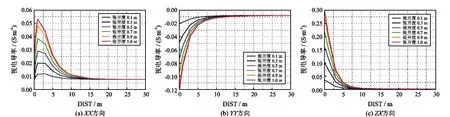
图5 裂缝空间位置和张开度对视电导率的影响(X/Y双线圈系结构)

由图5可以看出：

(1)XX方向，由于在层边界的电荷积累引起的“羊角”现象[16]，裂缝与仪器距离DIST小于3 m时，视电导率值单调上升，大于3 m时，视电导率单调下降，具有探测能力；YY和ZX方向，仪器距离裂缝0～30 m的范围内视电导率值均有单调性，具有探测能力；

(2)同一空间位置时，裂缝张开度越大，视电导率值越大。YY和ZX单调性相反，同一张开度时，裂缝与仪器距离越近，视电导率绝对值越大；

(3)根据XX、YY和ZX3个方向视电导率值变化规律，可以识别裂缝在不同空间位置和张开度的唯一视电导率数值，即X/Y双线圈系结构可以识别不同空间位置和不同张开度的裂缝。

2.1.2 线圈发射频率的影响

与2.1.1模型参数相同，发射频率调整为20 kHz，再次进行计算。选择裂缝张开度分别为0.1 m和1.0 m的情况下，进行发射频率1 kHz和20 kHz的对比。绘制图形如图6所示。

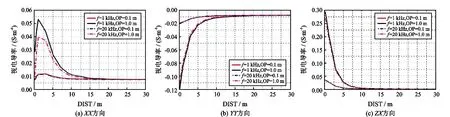
图6 线圈发射频率对视电导率的影响(X/Y双线圈系结构)

由图6可以看出：

(1)在XX方向，当张开度为1.0 m时，在仪器距离裂缝0～30 m的范围内，1 kHz测得的视电导率值略大于20 kHz测得的视电导率值；当张开度为0.1 m时，在仪器与裂缝0～30 m的范围内测量的视电导率值基本相同；

(2)在YY和ZZ方向，裂缝张开度分别为0.1 m和1.0 m时，不同频率情况下，在仪器距离裂缝0～30 m的范围内测得的视电导率值基本相同。

2.2 角度变化裂缝模型

裂缝0°时垂直于围岩中，与仪器平行，将裂缝绕Z轴或Y轴旋转180°。此模型主要研究方位角和俯仰角影响下的响应特性。由2.1知发射频率对多分量远探测仪器探测井旁裂缝几乎没有影响，后续研究都选择发射频率为20 kHz。研究裂缝方位角和俯仰角时，固定裂缝与仪器的距离，改变裂缝方位角或俯仰角，研究裂缝张开度分别为0.1 m和1.0 m情况下其响应曲线特征规律。具体模型参数见表4。

表4 角度变化裂缝模型参数

2.2.1 裂缝方位角的影响

在此模型中裂缝绕Z轴旋转即是改变裂缝的方位角，0°时仪器与裂缝相对位置最远，90°时仪器与裂缝相对位置最近。按照表3中的数据进行模拟。绘制图形如图7所示。

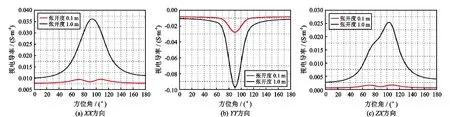
图7 裂缝方位角对视电导率的影响(X/Y双线圈系结构)

由图7可以看出：

(1)裂缝张开度为1 m时，在XX和YY方向，随着仪器与裂缝的相对位置不断接近，视电导率的值和变化幅度逐渐增大，在方位角为90°时，视电导率取得最大值。在ZX方向，方位角90°，受裂缝与仪器衔接的影响，视电导率最大值出现偏移。裂缝张开度减小为0.1 m，XX和ZX方向，在方位角为75°～105°时，视电导率反转。

(2)不考虑裂缝与仪器衔接的影响，视电导率值变化规律关于方位角为90°对称，利用单一方向线圈的视电导率值无法判断裂缝的方位角是0°～90°还是90°～180°。但是同时利用多组方向线圈，就可以通过视电导率值判断得到裂缝的方位角。

2.2.2 裂缝俯仰角的影响

在此模型中裂缝绕Y轴旋转即是改变裂缝的俯仰角，当俯仰角达到30°时，裂缝开始穿过仪器，当俯仰角达到105°时，裂缝开始离开仪器。按照表3中的数据进行模拟。绘制图形如图8所示。

图8 裂缝俯仰角对视电导率的影响(X/Y双线圈系结构)

由图8可以看出：

(1)在XX和YY方向，裂缝进入(30°～75°)或离开(105°～150°)仪器的时候视电导率值会出现一次反转。ZX方向只在裂缝进入(30°～75°)仪器的时候视电导率值出现反转；

(2)裂缝穿过仪器(75°～105°)的影响，在XX和YY方向，视电导率最大值出现前移，裂缝张开度越大，影响越大。ZX方向视电导率最大值出现了后移，裂缝张开度越大，影响越大；

(3)利用X/Y双线圈系结构判断穿过仪器裂缝的俯仰角，需要先分析进入、穿过或离开裂缝时的视电导率值，然后结合多组方向线圈去识别不同俯仰角的裂缝。

3 结 论

通过建立多分量电磁远探测仪的井旁裂缝响应模型，模拟计算了发射频率、裂缝张开度、裂缝的空间位置、裂缝方位角和裂缝的俯仰角的响应特性，探究了多分量电磁远探测仪器的井旁裂缝响应的敏感性。得到以下结论：

(1)利用多分量电磁远探测仪器，对井旁裂缝的研究表明，裂缝的张开度越大，即裂缝的体积越大，获得的视电导率数值也就越大；裂缝与仪器的距离越近，响应就越明显。裂缝张开度和裂缝离仪器的距离与视电导率值有着一一对应的特性，即裂缝可被仪器清楚地探测到；

(2)在本文模拟的情况下，如果排除层边界电荷积累引起的误差，X/Y双线圈系结构在XX，YY，ZX3个方向在仪器距离裂缝0～30 m内均有单调变化，仪器可以探测裂缝的空间位置，其余分量(未在文中给出)都因数值太小且不单调变化，不能用来探测裂缝；

(3)多分量远探测仪器X/Y双线圈系结构，线圈发射频率对裂缝的响应几乎没有影响；

(4)探测裂缝的方位角或者俯仰角时，需要识别裂缝的方位角或俯仰角是0°～90°还是90°～180°，需要选择多组方向的线圈来判断。当改变裂缝的方位角或裂缝的俯仰角，多分量远探测仪器依然可以识别到裂缝的张开度或空间位置。