微震信号初至拾取的AIC算法及其分析

赵震华，张杏莉，卢新明

(1.山东科技大学 计算机科学与工程学院，山东 青岛 266590；2.山东科技大学 山东省智慧矿山信息技术重点实验室，山东 青岛 266590)

在冲击地压微震监测技术中，微震信号P波初至到时对于震源准确定位、冲击地压预测预警具有重要的意义[1]。微震信号初至拾取的高准确性是实现震源定位可靠性的前提。

目前，国内外针对微震信号初至拾取的方法主要有赤地信息量准则(Akaike information criterion,AIC)算法[2-3]、长短时窗平均能量比法(short-term average/long-term average,STA/LTA)[4-5]、高阶统计量法[6]、人工神经网络法[7-8]等。STA/LTA方法是目前常用的微震事件识别方法，利用时域信号短时窗能量平均值和长时窗能量平均值之比动态反映信号振幅变化，通过识别微震事件的初至时刻达到自动检测微震事件的目的。该方法实现简单，运算速度快，但误判率较高。高阶统计量法通过从非高斯信号的高阶统计量中获取有效信息，根据高阶统计量中的峰度或偏斜度曲线的变化自动拾取震相到时，是研究非高斯、非线性和非平稳信号的有力工具，但在信噪比低时识别精度较差[9]。人工神经网络法在拾取震相初至时，一般将表征地震波的特征量如偏振特征、信噪比、频谱特征、振幅等作为输入参数，将震相类别作为输出，并使用样本集训练该网络使之获得模式分类识别功能，最后将地震波某一特征量输入训练好的网络，若输出值大于设定好的阈值，就认为获得了震相的类型。人工神经网络法具有良好的非线性映射功能，可并行处理大量信息，但存在工作量大、难以选择隐含层节点数和传递函数的缺点。

AIC算法是目前应用最广泛、拾取精度较高的震相初至拾取算法之一，具有运算速度快、拾取准确率高、噪声鲁棒性强等特点。王李管等[10]利用长短时窗法初步定位P波S波的到时区间，在到时区间内应用自回归赤池信息准则(auto regression-Akaike information criterion,AR-AIC)算法，计算出对应P波S波的初至到时，并结合时差阈值判别和时频图谱对拾取结果进行检测；贾瑞生等[11]利用Hilbert变换计算出包络信号，设置包络阈值，搜索出震相初至的大致位置，并设置合适的时窗，利用VAR-AIC算法计算P波震相初至；尚雪义等[12]利用经验模态分解(empirical mode decomposition,EMD)自适应地将地震数据和噪声分离为不同的本征模式函数(intrisic modcel function,IMF)，可靠地保留了P波震相到达幅值和相位谱，利用VAR-AIC算法识别P波初至。本研究对AR-AIC、VAR-AIC算法及其影响因素进行全面分析对比，并结合实测煤矿井下微震信号的处理，分析AR模型阶数、特征函数、时窗长度对算法效果的影响。

1 AIC算法简介

AIC[13]算法是由日本统计学家赤池弘次创立和发展的。AR-AIC[2]算法是一种基于AIC信息准则的到时拾取方法，该方法基于微震信号的非平稳特征，将信号划分成若干个固定长度的波形段，然后进行自回归(auto regression,AR)处理，求解AR模型阶数和系数，AR-AIC算法表示为[14]

(1)

Maeda[3]对AR-AIC算法进行改进，提出VAR-AIC算法，该算法直接由微震波形数据计算AIC函数，求解AIC函数的最小值，该最小值对应的位置即为震相初至。VAR-AIC算法表示为

VAR-AIC(k)=kln{VAR(CF(Xt[1,k]))}+(N-k-1)ln{VAR(CF(Xt[k+1,N]))}。

(2)

式中：Xt[1,k]为微震波形数据Xt中采样点1～k的振幅值，k的范围为时间窗口内所有的微震信号采样点，N为微震信号长度，VAR()为方差函数，CF()为特征函数。VAR-AIC算法计算简单，拾取精度高，因此得到广泛应用。

2 AIC算法的影响因素分析及参数确定

由式(1)和式(2)可知，影响两种AIC算法拾取精度的因素有AR模型阶数、特征函数和时窗长度。本部分对两种AIC算法的影响因素进行分析讨论并确定各参数的取值。

2.1 阶数M的选取

AR模型阶数M最常用的确定方法是AIC准则[15]，AIC准则的表达式为

AIC(M)=Nlnσ2+2M。

(3)

式中：M为AR模型阶数；N为微震信号长度；σ2为AR模型系数。取式(3)最小值时的M，即为AR模型阶数。利用式(3)得到某微震信号的AIC准则曲线如图1所示。

图1 AIC准则曲线图Fig. 1 AIC criterion curve

由图1可见，AIC(M)值在M=100时已经基本趋于稳定，在M=265时到达最小值。M取25、50、100、200、265和300时，AR-AIC算法对某微震信号的拾取结果如图2所示。

(a)为手工拾取结果；(b)～(g)分别为AR-AIC算法在M为25、50、100、200、265和300时的拾取结果。图2 不同AR模型阶数M影响计算结果Fig. 2 Calculation results of difference AR model order M

由图1和图2可知，当M=50和100时，M值偏小，AIC(M)值还未稳定，AR-AIC算法拾取结果与手工拾取结果差距较大；当M=200和265时，AIC(M)值已基本稳定，拾取结果与手工拾取结果差异较小；当M=300时，AIC(M)值已经稳定，拾取结果与手工拾取结果差异相对较小。结果表明AIC准则确定的AR模型阶数能够使AR-AIC算法取得相对良好的效果。

AR-AIC算法的计算时间会随着AR模型阶数M的增大而增加。以长度N=4 000的微震信号为例，使用AR-AIC算法在不同阶数M下的计算时间见表1。由表1可知，当M值增大时，算法耗时会显著增加。因此，在选择AR模型阶数时，建议选择AIC(M)最小值时的阶数M或者选择AIC(M)最小值稍前的阶数M，但还需不断计算，以保证该M值时拾取的初至到时与AIC(M)最小值时的M值拾取的初至到时相差不大，既保证拾取结果，又能适当降低算法运行时间。

表1 不同AR模型阶数M的计算时间Tab. 1 Calculation time of different AR model order M

2.2 特征函数的选取

特征函数对微震信号的初至到时拾取至关重要，选取对微震信号振幅和频率变化反应灵敏的特征函数，会提高算法对微震信号初至到时的拾取精度。

如式(2)所示，VAR-AIC算法的主要影响因素是能够影响微震波形的特征函数(characteristic function，CF)，特征函数的选取会直接影响初至到时拾取的结果[16]。目前常用的特征函数有：

CF1(i)=|Xt(i)|，

(4)

(5)

CF3(i)=Xt(i)-Xt(i-1)，

(6)

(7)

CF5(i)=SUM(|Xt(i)|)，

(8)

(9)

(10)

利用7种特征函数分别对余弦函数进行分析，对振幅变化的响应特征如图3所示。

(a)和(i)为振幅变化的余弦信号；(b)和(j)、(c)和(k)、(d)和(l)、(e)和(m)、(f)和(n)、(g)和(o)、(h)和(p)分别为特征函数CF1～CF7的拾取结果。图3 7种特征函数对振幅变化的响应Fig. 3 Response of 7 characteristic functions to amplitude variation

由图3可见，特征函数CF1～CF7对图3(a)的余弦信号振幅变化皆有响应，其中CF4在分段点处的VAR-AIC值变化最大，响应最灵敏；CF7相比其他特征函数的响应程度稍弱一点。特征函数CF1～CF6对图3(i)的余弦信号振幅变化皆有响应，其中CF4的响应最灵敏；CF7的响应最弱，并且拾取到错误的分段点。

对频率变化的响应特征如图4所示。特征函数CF1、CF2、CF5和CF6对图4(a)和图4(i)余弦信号频率变化没有响应，CF3和CF4对频率变化有响应。相比CF3，CF4在分段点处的VAR-AIC值变化更大，响应更为灵敏，CF7虽对频率变化有响应，但响应程度较弱。

(a)和(i)为频率变化的余弦信号；(b)和(j)、(c)和(k)、(d)和(l)、(e)和(m)、(f)和(n)、(g)和(o)、(h)和(p)分别为特征函数CF1～CF7的拾取结果。图4 7种特征函数对频率的响应Fig. 4 Response of seven characteristic functions to frequency

由此得出的7种特征函数对振幅和频率变化的响应特性见表2。

表2 7种特征函数对振幅和频率的变化响应特性Tab. 2 The response characteristics of seven characteristic functions to the variations of amplitude and frequency

图5为VAR-AIC算法在7种特征函数作用下的某实测微震信号初至拾取结果。可见，VAR-AIC算法对 7种特征函数作用下的微震信号都能进行初至拾取，但拾取结果受到一定影响。图5(d)和图5(e)中，CF3和CF4作用下的微震信号拾取结果比CF1、CF2、CF5、CF6和CF7更接近手工拾取结果，拾取结果更优，故建议选用特征函数CF3或CF4来进行微震信号初至拾取。

(a)为手工拾取结果；(b)～(h)分别为特征函数CF1～CF7作用下VAR-AIC算法拾取结果(虚线)图5 不同特征函数VAR-AIC算法拾取结果Fig. 5 VAR-AIC algorithm picks the first arrival results using different characteristic functions

2.3 时窗长度

在VAR-AIC算法实际计算过程中，会出现AIC函数最小值不在信号初至位置的情况，如图6所示。

(a)为某微震信号；(b)为VAR-AIC算法拾取错误初至图6 VAR-AIC算法拾取错误初至Fig. 6 VAR-AIC algorithm picks up error first arrival

为避免此类情况的发生，将微震信号的振幅最大值时刻p作为时窗的结束时刻(如图7)，从p向前取长度为l个采样点为初至拾取时窗，并在时窗内计算AIC函数最小值。为了分析时窗长度对拾取结果的影响，分别取l为200、400、600、1 000和1 200个采样点，且特征函数选择CF4，此时式(2)变为

图7 振幅最大值时刻pFig. 7 Maximum amplitude moment p

VAR-AIC(k)=kln{VAR(CF4(Xt[p-l,k]))}+
(N-k-1)ln{VAR(CF4(Xt[k+1,p]))}。

(11)

式中，p为振幅最大值时刻，l为时窗长度。

VAR-AIC算法对图7所示的微震信号拾取结果如图8所示。图8(a)～8(f)分别为时窗长度为200、400、600、800、1 000和1 200 个采样点的拾取结果，矩形框表示时窗长度。

图8 不同时窗长度的VAR-AIC算法拾取结果Fig. 8 VAR-AIC algorithm picks up signals with different time window lengths

由图8可见，时窗长度对VAR-AIC算法的拾取结果有较大影响。图8(a)和图8(b)的拾取结果与手工拾取结果相差较大，而图8(c)～8(f)的拾取结果与手工拾取结果误差仅为8个采样点。可见，当时窗长度过小时，时窗内手工拾取点后的微震数据占总时窗长度的25%以上，计算初至点前的方差偏大，从而导致拾取的初至点稍靠后。为保证拾取结果的准确性，建议在选择时窗长度时，开始时刻为信号最大振幅时刻向前移动600～1 000个采样点，结束时刻选择信号最大振幅时刻，且时窗内需要包含信号初至时刻。

3 影响因素实例验证

3.1 AR模型阶数M的选取

选取10条实测微震信号记录编号1～10，如图9所示。

图9 10条实测微震信号记录Fig. 9 10 micro-seismic signal records

利用AIC准则得到10条微震信号记录的AIC(M)的最小值，并利用AR-AIC算法得到各阶数M下的初至时刻结果如表3所示，AR-AIC算法的计算用时如表4所示。

表3 各阶数M下的初至时刻Tab. 3 The first arrival time of each order ms

由表3可知，在AIC(M)最小值时的阶数M的拾取结果相比于其他阶数的结果更接近手工拾取，效果更好。由表4可知，运行时间会随着阶数的增大而增加，因此阶数M应选择AIC(M)最小值时的阶数M或者选择AIC(M)最小值稍前的阶数M，既保证拾取效果，也尽可能减少算法的计算时间。

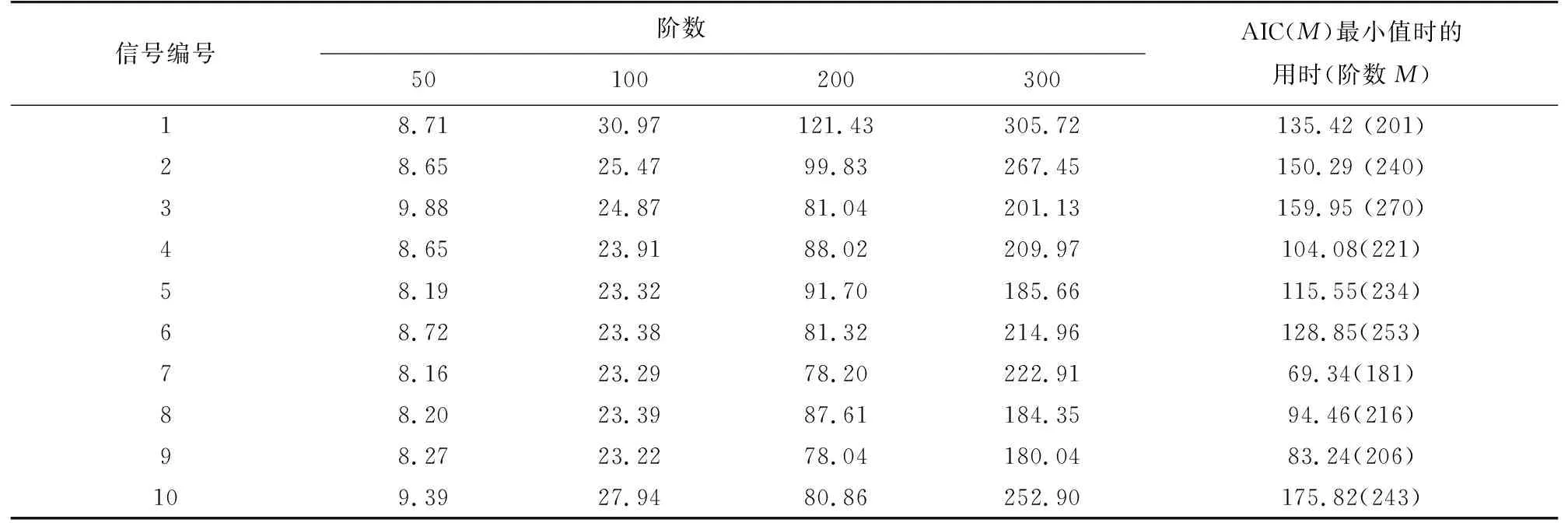
表4 AR-AIC算法在各阶数M下的计算用时Fig. 4 Running time of AR-AIC algorithm in different orders M s

3.2 特征函数的选取

选取图9中的10条实测微震信号，利用VAR-AIC算法分别计算10条微震信号记录在不同特征函数下的拾取结果，如表5所示。

表5 不同特征函数下的初至时刻Tab. 5 First arrival time under different characteristic functionsms ms

由表5可知，与手工拾取相比，特征函数CF4作用下的微震信号更接近于手工拾取结果，鲁棒性更强，因此特征函数选择CF4。此外，其他特征函数作用的微震信号在拾取初至时会出现拾取错误的情况，与图6所示结果一样，原因为初至时刻的AIC值不是AIC函数的全局最小值，导致拾取错误。

3.3 时窗长度的选取

同样选取图9所示的10条微震信号，利用式(11)计算10条微震信号记录在不同时窗长度下的拾取结果，特征函数选择CF4。时窗的开始位置为结束位置向前移动的时窗大小，结束位置为最大振幅值时刻，拾取结果如表6所示。

由表6可知，与特征函数CF4的拾取结果相比，时窗长度在200～400 个采样点之间的拾取效果与CF4的拾取效果相差较大，600～1 200 个采样点之间的拾取效果更接近于特征函数CF4的拾取结果，鲁棒性更强，故时窗长度应选择在最大振幅值之前的600～1 200个采样点。

表6 不同时窗长度下的初至时刻Tab. 6 First arrival time under different window lengthms

通过对以上10条实测微震信号记录的研究及分析，得出的结论与第2部分中给出的建议基本一致，验证了所得结论的正确性。

4 AIC算法应用分析

利用两种AIC算法及其改进算法拾取微震信号初至应用较多。由于AR-AIC算法本身存在计算量巨大、拾取精度不高、计算时间长等缺点，决定了该算法在微震信号初至拾取中应用相对较少。Leonard[17]和王海军等[18]分别对AR-AIC算法进行改进，提出混合初至估计的方法，改善了低信噪比震相的拾取效果。而在改进VAR-AIC算法时，一种思路是对待拾取的信号波形进行改变，例如本研究利用特征函数作用于信号波形，使其对信号初至拾取产生影响。刘希强等[19]提出利用三阶累积量进行精细震相拾取的TOC-AIC(third-order cumulant AIC)算法，即用两个时间段数据的三阶累积量代替VAR-AIC算法中的方差。TOC-AIC算法无论是在信噪比较低还是较高的情况下，得到的震相初至结果与实际结果都非常接近。

由于VAR-AIC算法存在拾取错误的问题，衍生出另外一种思路，即对微震信号长度进行限制，避免拾取错误。崔云洁等[20]应用小波阈值降噪方法对微震信号进行降噪，利用STA/LTA方法进行预拾取，获取初至大致时刻，并以该时刻为基准，向前向后各截取500个采样点构成时间窗口，在时窗内利用VAR-AIC算法拾取初至；朱权洁等[16]对原有的小波包去噪法模型进行改造，建立基于多去噪规则的多阈值去噪法，在VAR-AIC算法的基础上，提出了具有时窗限制的I-AIC(improved AIC)算法，精确拾取水力压裂微震信号P波初至，与其他4种方法相比，I-AIC算法对去噪结果更为敏感，拾取精度、计算速度更优。

通过对上述几种AIC改进算法的应用分析，说明对两种AIC算法的影响因素进行研究很有必要，可以为AIC算法在特征函数或时窗长度上进一步改进，以获得精度更高的初至拾取结果提供参考。

5 结论

通过对AIC算法的实验和应用分析，得出以下结论：

1) AR-AIC算法中，AR模型阶数M对拾取初至结果有较大影响。M值越大，算法复杂度越高，建议选择AIC(M)最小值时的阶数M或者选择AIC(M)最小值稍前的阶数M，该M值下算法拾取的初至点与AIC(M)最小值时的阶数M值拾取的初至点相差较小。这样既能保证拾取效果，又能适当降低算法计算用时。

3) 为避免拾取错误，应确定合适的时窗长度，建议时窗长度为600～1 000个采样点，时窗内需包含信号初至，时窗结束时刻通常选择信号最大振幅值时刻，时窗开始时刻为信号最大振幅时刻向前移动600～1 000个采样点。这样既能保证拾取效果、减少拾取误差，又缩短了计算时长。