具有垂直传染的离散SIS传染病模型的动力学性质
陈雨青,冯舒婷,岑泳欣,周效良
(1. 河海大学理学院,江苏 南京 211100; 2. 岭南师范学院数学与统计学院,广东 湛江 524048)
0 引言
一直以来,疾病是人类死亡的主要原因之一,传染病却是能危害更多人死亡的疾病,随着气候变暖、环境恶化,一些新型的恶性传染病带来的问题日益突出.人们对传染病的认识逐渐加深,通过建立合适的传染病模型,达到控制和治疗疾病的效果,是研究离散传染病模型的真正意义所在[1-2].
最近几年,人们越来越关注离散SIS(susceptible-infected-susceptible)传染病模型的研究,而且得到了丰富的研究成果[3-6],其中模型平衡点的稳定性、疾病的持久性、灭绝性以及模型分岔等动力学性态是大多数学者热衷研究的问题.例如Castillo-Chavez等[4]建立了一类离散 SIS 传染病模型,分析了该模型的动力学行为.王振国等[5]研究了一类具有非线性传染率的SIS 网络传染病模型的动力学行为,讨论了该模型的跨临界分岔.Allen等[6]提出了一类SI、SIR和SIS离散传染病模型,分析了这类模型平衡点的稳定性.
考虑染病的母亲把疾病传染给婴儿的概率为p(0 (1) 其中:Λ指易感者的常数输入,β指传染率系数,b,d分别表示出生率和死亡率,B表示输出率,α表示因病死亡率,γ表示染病者的恢复率.模型中所有参数为正常数且垂直传染率为1.将模型(1)离散化得到 (2) 模型(1)的基本再生数为 本文首先探讨系数参数对特征值的影响,得到双曲平衡点的类型及其稳定性.接下来,对于非双曲的平衡点,利用中心流型定理研究了模型(2)无病平衡点E0的跨临界分岔和flip分岔,以及地方病平衡点E*的跨临界分岔.最后,我们给出模型(2)分岔的生物学解释. 定理1平衡点Eo有以下性质: (ⅰ)如果R0∈l1,l2,平衡点Eo非双曲; (ⅱ)如果R0∈C0,平衡点Eo渐近稳定; (ⅲ)如果R0∈C1,C2,平衡点Eo为不稳定结点. 定理2平衡点E*有以下性质: 定理3当R0=1时,无病平衡点E0将产生跨临界分岔.具体过程如下:在R0=1处实施微小的扰动使得R0<1时,E0双曲且稳定,E*双曲且不稳定,使得R0>1时,E0双曲且不稳定,E*双曲且稳定,在R0=1处,平衡点E0非双曲. 证明对于平衡点E0,当R0=1时,有λ2=1,λ1=1-ϑ,把ξ1=R0-1看做分岔参数,将J(E0)写为Jξ1(E0),得到 其特征值λ1和λ2对应的特征向量为(1,0)τ,(w1,1)τ.其中 令 并利用变换(S,I)τ=T(u,v)τ,将系统(2)变为 (3) 由文献[8]定理2.2.4可知,在ξ1附近平衡点(u,v)=(0,0)的稳定性与分岔可通过其在中心流型上一参数族映射来确定,中心流型形式如下: Wloc(0,0)={(u,v,ξ1)∈R3|u=h(v,ξ1),h(0,0)=0,Dh(0,0)=0,|v|<δ,|ξ1|<δ}. (4) 将式(4)代入式(3),可得一维映射 (5) 验证下面式子成立: (6) 定理4当R0∈l2时,系统(2)在无病平衡点E0经历flip分岔;具体地讲,当α2>0时,系统(2)在平衡点E0分岔的2周期轨稳定;当α2<0时,系统(2)在平衡点E0分岔出的2周期轨不稳定. 其中 系统(2)在不动点E0经历flip分岔需满足: 其中 由文献[9]定理3.5.1可知,当R0∈l2时,平衡点E0经历flip分岔. 定理5当R0=1时,模型(2)在地方病平衡点E*产生跨临界分岔,其双曲性和稳定性的变化与定理3所述相同. 证明对于平衡点E*,当R0=1时,有λ2=1,λ1=1-ϑ,把ζ=R0-1看做分岔参数,将J(E*)写为Jζ(E*)得到 利用变换将模型(2)变为 (7) 解得 故式(8)表达式为 (8) 将式(8)代入式(7)得到 通过计算验算如下式子成立: 从而模型(2)在E*产生跨临界分岔. 在本节,我们对于模型(2)给出一些数值模拟结果,对理论研究进行验证. 例1令Λ=0.03,β=0.1,α=0.1,b=0.1,d=0.1,p=0.5,q=0.5,B=0.05,γ=0.1,通过计算,R0<1,选取3组初始值(S0,I0)为:(1.8,0.3),(1.6,0.4),(1.3,0.5),从图1可知E0(0.6,0)是稳定的. 选取Λ=0.3,β=0.1,α=0.1,b=0.1,d=0.1,p=0.5,q=0.5,B=0.05,γ=0.1,并选取3组初始值(S0,I0)为:(1.2,1.3),(1.6,0.4),(1.3,0.7),如图2所示,满足当R0>1时,E*全局渐近稳定. 从图1和图2可以看出:当R0<1时,E0稳定,而E*不稳定;当R0>1时,E*稳定,而E0不稳定.因此在平衡点E0和E*处均产生跨临界分岔. 图1 E0稳定Fig.1 E0is stable图2 E*稳定Fig.2 E*is stable 图3 flip分岔Fig.3 Flip split

1 平衡点性质




2 跨临界分岔与flip分岔

2.1 无病平衡点Eo的跨临界分岔与flip分岔








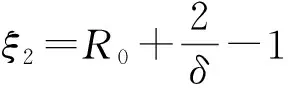


2.2 地方病平衡点E*的跨临界分岔





3 数值模拟



4 分岔的生物学解释


