一种零耦合度及部分运动解耦的空间2T1R并联机构动力学建模

汤 耀， 沈惠平， 曾博雄， 杨廷力

(常州大学 现代机构学研究中心, 江苏 常州 213164)

具有转动和移动混合输出的2T1R空间并联机构，因其驱动元件少、制造容易等特点，在空间抓取、调整姿态等操作中，具有较广泛的应用价值[1-6]。

对一个有待研发的并联机器人而言，建立一个精度高且响应快的动力学模型至关重要[7-9]。常用的动力学建模方法主要有：Lagrange法、Newton-Euler法、虚功原理法等[10-12]。Lagrange法根据动能和势能推导出动力力学模型，对于多杆件机构，此方法计算量大，且无法求解系统运动副处的支反力；Newton-Euler法通过对各杆件单独分析求得各关节的约束力，再通过消除各杆件的相互作用力，来建立完整的动力学模型，该方法建模思路清晰，但其推导过程复杂，计算量也大；虚功原理法根据系统的虚位移做功推导动力学模型，在计算过程中只需求解少数速度矩阵和作用力，因此，具有高效、方便的特点，但不能求得运动副反力。

进一步，杨廷力[13]提出了用于动力学建模的基于虚功原理的序单开链法，该方法的建模基本单元是子运动链(SKC)，不仅具有传统虚功原理计算过程简洁的优点，而且能够求出各SKC连接处的运动副支反力，这对机构构件的强度计算、结构设计以及机械振动研究等具有重要的作用。

在研究对象方面，对6-DOF并联机构，丁华锋等[14]基于虚功原理建立了一种新型6-DOF并联机构的动力学数学模型；对5-DOF并联机构，陈修龙等[15]基于虚功原理，对4-UPS-UPU机构进行动力学分析；张东胜等[16]还研究了5-DOF混联机器人的逆动力学；而4-DOF并联机构方面，蔡善乐等[17]运用虚功原理法，对2PRS-2UPS并联机构进行动力学分析；3-DOF并联机构方面，高征等[18]、陈子明等[19]，分别利用拉格朗日法和虚功原理，对三自由度旋转台、对称两转一移3-UPU并联机构的动力学进行分析；贾晓辉等[20]采用虚功原理方法，推导出3-RRPR柔性机构的动力学逆解模型，并给出了系统固有频率的求解表达式。尤晶晶等[21]针对一种具有解析位置正解的新型三自由度并联机构，求解了其逆向动力学方程。

本课题组设计、提出的一种新型3-DOF空间2T1R并联机构2P(Pa2R)2R-P(PaR)[22]，首先进行运动学分析，求得该机构每个构件的速度、加速度，然后，使用基于虚功原理的序单开链法，建立其逆向动力学模型，求解验证了该机构的驱动力和SKC连接处的支反力；并分析比较了不同广义坐标下的动力学方程求解的时间。为该机构的样机设计和动力学优化提供了技术依据。

1 2T1R并联机构的设计

本文研究的一种新型3-DOF空间2T1R并联机构，为零耦合度、部分运动解耦，且具有符号式位置正解，它由静平台0、动平台1和2条混合支链组成[22]，如图1所示。

图1 2T1R并联机构简图Fig.1 Structure diagram of the 2T1R PM

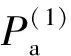
该机构具有4个优点：①仅由移动副和转动副组成，有利于制造、安装；②因机构的耦合度k=0，具有正向位置符号解，有利于误差分析、尺度综合、刚度分析及动力学研究等；③机构沿Y轴方向的位置仅由驱动副P1，P2决定，因此，该机构具有部分输入-输出运动解耦性，有利于机构的轨迹规划及运动控制；④该机构操作工作空间大，不仅适用于小范围内的两平移一转动(如抓取、喷涂)等精密操作(当3个移动副取不同的速度时)，也能用于沿导轨方向大范围内的一维移动(如工件搬运、传输等)运动输出(当3个移动副取相同速度时)，因此，具有潜在的应用前景。

2 运动学分析

2.1 位置分析

机构的运动学模型如图2所示，静坐标系O-XYZ的坐标原点O为静平台0的几何中心，Y轴方向平行于A1A2连线，Z轴平行于静平台0所在平面的法线方向，并指向动平台1；动坐标系O′-X′Y′Z′的原点位于动平台1的几何中心，X′轴、Y′轴分别重合、垂直于D2C3连线，而X轴、Z′轴方向均由右手定则确定。

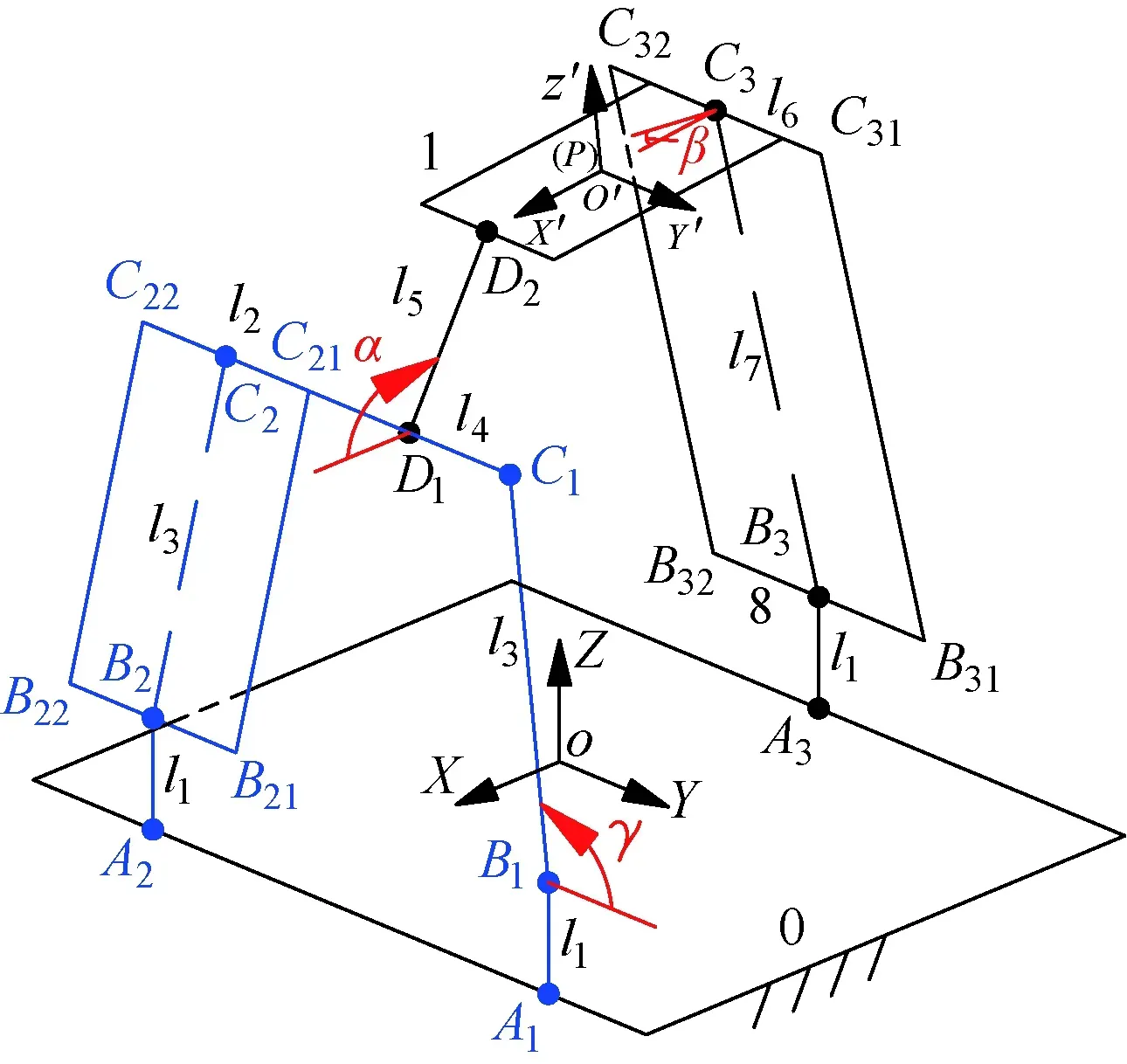
图2 2T1R机构整体运动学建模Fig.2 Integral kinematics modeling of 2T1R PM

机构的尺寸标注为：A1B1=A2B2=A3B3=l1，混合支链Ⅰ上B1C1=B21C21=B22C22=l3，C21C22=l2，C1C21=l4，D1D2=l5。混合支链Ⅱ中，B31C31=B32C32=l7，C31C32=l6。静平台0上两导轨之间间距为2b；动平台1上D2C3=2d。B1C1与Y轴正向的夹角为γ；D1D2与X轴正向的夹角为α；D2C3与X轴正向夹角为动平台输出姿态角β，以沿Y轴逆时针方向为正方向。

在静坐标系O-XYZ下，由文献[22]易知：A1=(b,yA1,0)；A2=(b,yA2,0)；A3=(-b,yA3,0)；B1=(b,yA1,l1)；B2=(b,yA2,l1)；B3=(-b,yA3,l1)；α=arccos[(2dcosβ-2b)/l5]。

设动平台P(y，z)及姿态角β，易求得：C1=(b,y+l4/2,z-dsinβ-l5sinα)；C2=(b,y-l4/2-l2/2,z-dsinβ-l5sinα)；C3=(-b,y,z+dsinβ)；D1=(b,yA1+l3cosγ-l4/2,l1+l3sinγ)。

由3个几何约束条件，建立位置约束方程为

(1)

2.2 速度与加速度分析

2.2.1 子运动链Ⅱ中各杆件

1) 动平台

设P点的输出速度为v1=[y′z′β′]T，驱动移动速度为v2=[y′A1y′A2y′A3]T，对式(1)两边关于t求一阶导数、二阶导数，可得：

Jpv1=Jqv2

(2)

Jpv′1-Jqv′2+K=0

(3)

f12=zC1-zB1，f13=(-dcosβ-2dsinβcotα)(zC1-zB1)，f21=u22=yC2-yB2，f22=zC2-zB2，f23=

(-dcosβ-2dsinβcotα)(zC2-zB2)，f31=u33=yC3-yB3，f32=zC3-zB3，f33=dcosβ(zC3-zB3)，K1=

机构非奇异时，Jp可逆，由式(2)、式(3)可得：

(4)

(5)

式(4)、式(5)为动平台1上P点的输出速度、输出加速度。

为了便于后续计算，现将动平台1的速度矩阵分解为平动矩阵和转动矩阵，即：

(6)

(7)

同理，可求出点D2、点C3的速度和加速度矩阵分别为：

(8)

(9)

(10)

(11)

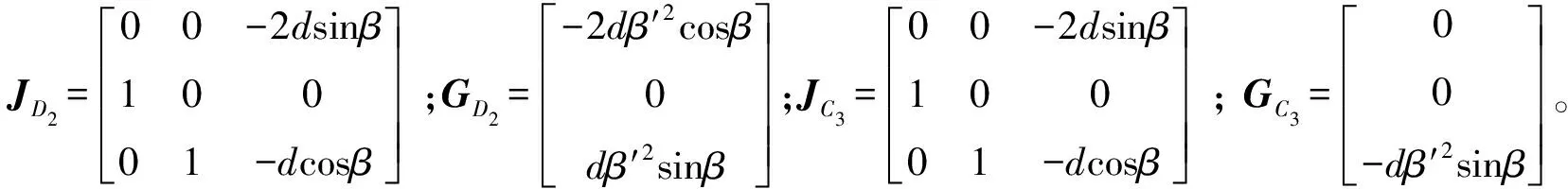
2) 驱动滑块A3B3

滑块A3B3质心的速度、加速度分别为：

vs3=Jv s3v2

(12)

as3=Jv s3v′2

(13)

3) 杆件B3C3

将B31C31，B32C32杆件的运动等效为杆件B3C3进行分析。易知，C3点的速度为

vC3=vs3+ωu3×e3·l7=Jv C3v2

(14)

式中：ωu3为杆件B3C3的角速度；e3为杆件B3C3的单位矢量。

对式(14)两边同时叉乘e3，整理得ωu3

(15)

杆件B3C3质心的速度矩阵表示为

(16)

进一步，对式(14)求导，得C3点的加速度为

aC3=as3+εu3×e3·l7+ωu3×(ωu3×e3)·l7

(17)

对式(17)两边同时叉乘e3，可得杆件B3C3的角加速度为

(18)

将式(16)求导，得杆件B3C3的质心加速度为

au3=as3+εu3×e3·l7/2+ωu3×(ωu3×e3)·l7/2=(as3+aC3)/2

(19)

4) 杆件C31C32

杆件C31C32质心的速度、加速度分别为：

vs5=vC3=Jv s5v2

(20)

as5=aC3

(21)

5) 杆件D1D2

设D1点的输出速度为v3=[y′D1z′D10]T，驱动移动速度为v2=[y′A1y′A2y′A3]T，对满足杆长C1B1，C2B2的约束位置方程求导，一阶导数、二阶导数可表示为：

Jmv3=Jnv2

(22)

Jmv′3-Jnv′2+L=0

(23)

机构非奇异时，Jm可逆，由式(22)、式(23)得：

(24)

(25)

D1点的速度、加速度分别为：

(26)

aD1=G3v′3

(27)

易知，D2点的速度为

vD2=vD1+ωu4×e4·l5

式中：ωu4为杆件D1D2的角速度；e4为杆件D1D2的单位矢量。

得杆件D1D2的角速度、质心的速度分别为：

(28)

(29)

进一步，D2点的加速度为

aD2=aD1+εu4×e4·l5+ωu4×(ωu4×e4)·l5

杆件D1D2的角加速度、质心加速度分别为：

2.2.2 子运动链Ⅰ中各杆件

1) 杆件C1C22

杆件C1C22质心的速度、加速度分别为：

vs4=vD1=Jv s4v2

(30)

as4=aD1

(31)

2) 驱动滑块AjBj(j=1，2)

滑块AjBj(j=1，2)质心的速度、加速度分别为：

vsj=Jv sjv2

(32)

asj=Jv sjv′2

(33)

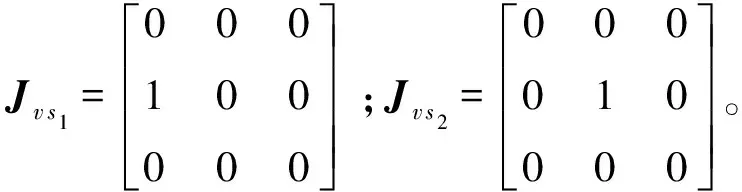
3) 杆件B1C1

易知，C1点的速度为

vC1=vs1+ωu1×e1·l3=Jv s4v2

(34)

式中：ωu1为杆件B1C1的角速度；e1为杆件B1C1的单位矢量。

对式(34)两边同时叉乘e1，整理得

(35)

杆件B1C1质心的速度的矩阵表示为

(36)

进一步，对式(34)求导，得C1点的加速度为

aC1=as1+εu1×e1·l3+ωu1×(ωu1×e1)·l3

(37)

对式(37)两边同时叉乘e1，可得杆件B1C1的角加速度为

(38)

进一步，将式(36)求导，得杆件B1C1的质心加速度为

au1=as1+εu1×e1·l3/2+ωu1×(ωu1×e1)·l3/2=(as1+aC1)/2

(39)

4) 杆件B2C2

将B21C21，B22C22杆的运动，等效为杆件B2C2进行分析。

同理，采用与杆件B1C1速度、加速度相同的求法，得到杆件B2C2的角速度、质心的速度分别为：

(40)

(41)

式中：ωu2为杆件B2C2的角速度；e2为杆件B2C2的单位矢量。

进一步，C2点的加速度为

aC2=as2+εu2×e2·l3+ωu2×(ωu2×e2)·l3

而杆件B2C2的角加速度、质心加速度分别为：

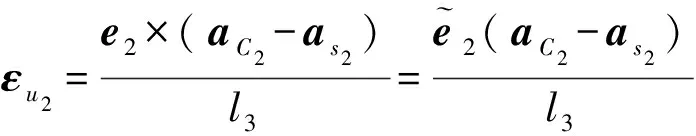
3 动力学分析

易知，杆件B21B22，A2B2及杆件B31B32，A3B3分别为同一个构件。

3.1 基于虚功原理的序单开链法基本原理

按上述结构分解的逆序，对各单开链进行动力分析，由单开链之间的约束关系和虚功原理，在理想约束下，外力(矩)和惯性力(矩)在机械系统的任何虚位移上的元功之和等于零，即可建立各SKC的动力学分析方程，其维度恰为机构耦合度k，在求出这k个未知支反力后，相应的驱动力(矩)可方便地直接求出[13]。

3.2 动力学建模与方程的生成

将移动副在驱动力作用下产生的位移定义为广义坐标，即q1=(yA1,yA2,yA3)T，对应产生的虚位移为δq1=(δyA1,δyA2,δyA3)T。

由式(6)～式(7)、式(12)～式(20)、式(28)～式(41)可建立各杆件的虚位移与驱动副的虚位移之间的关系式为：δXp=Jvp1δq1，δθp=Jwp1δq1，δXui=Jv uiδq1，δXsj=Jv sjδq1，δθui=Jw uiδq1(i=1～4，j=1～5)。

3.2.1 子运动链Ⅱ内各构件受力分析

1) 动平台

动平台在静坐标系{O}下的重力、惯性力、惯性力矩分别为：

动平台在工作时产生的力和力矩为：

2) 移动滑块A3B3

该滑块在静坐标系{O}下的重力、惯性力分别为：

oGs3=ms3og；ofs3=-ms3oas3

3) 移动杆C31C32

移动杆在静坐标系{O}下的重力、惯性力分别为：

oGs5=ms5og；ofs5=-ms5oas5

4) 转动杆(B3C3，D1D2)

转动杆在静坐标系{O}下的重力、惯性力、惯性力矩(i=3，4)分别为：

oGui=muiog；ofui=-muioaui；onui=-oIuioεui-oωui×(oIuioωui)

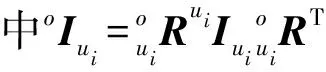
3.2.2 子运动链Ⅰ内各构件受力分析

1) 移动滑块(A1B1，A2B2)

移动滑块在静坐标系{O}下的重力、惯性力(j=1，2)分别为：

oGsj=msjog；ofsj=-msjoasj

2) 移动杆C1C22

移动杆在静坐标系{O}下的重力、惯性力分别为：

oGs4=ms4og；ofs4=-ms4oas4

3) 转动杆(B1C1，B2C2)

转动杆在静坐标系{O}下的重力、惯性力、惯性力矩(i=1，2)分别为：

oGui=muiog；ofui=-muioaui；onui=-oIuioεui-oωui×(oIuioωui)

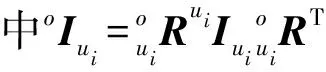
为简化动力学方程的计算，在静坐标系{O}下，将机构构件所受的外力(矩)，化简为各杆件质心位置的六维合力矢量。

动平台的六维合力矢量

(42)

移动杆(滑块)的六维合力矢量

(43)

转动杆的六维合力矢量

(44)

3.2.3 动力学方程的生成

解除联接2个SKC的运动副D1处的约束，则得到2个子系统，于是，支反力F4转化为作用在该2个子系统构件上的未知外力。由于2个SKC的耦合度均为0，其广义坐标与原系统的广义坐标相同，根据虚功原理可得，子运动链Ⅱ的动力学方程为

(45)

而子运动链Ⅰ的动力学方程为

(46)

式中F=(F1,F2,F3)T。

将式(6)～式(7)、式(12)～式(20)、式(28)～式(44)代入式(45)～式(46)，即可求出驱动力F1，F2，F3以及运动副D1处的支反力F4。

3.3 机构动力学分析实例

设机构的构件质量为：mp=0.031 7kg，ms1=0.022 1kg，ms2=0.036 7kg，ms3=0.039 7kg，ms4=0.023 7kg，ms5=0.014 8kg，mu1=0.056 0kg，mu2=0.112 1kg，mu3=0.127 4kg，mu4=0.041 5kg。

构件杆长与文献[22]一致，为：a=295mm，b=125mm，d=80mm，l1=20mm，l2=80mm，l3=230mm，l4=90mm，l5=170mm，l6=100mm，l7=280mm。

构件的转动惯量参数，见表1。

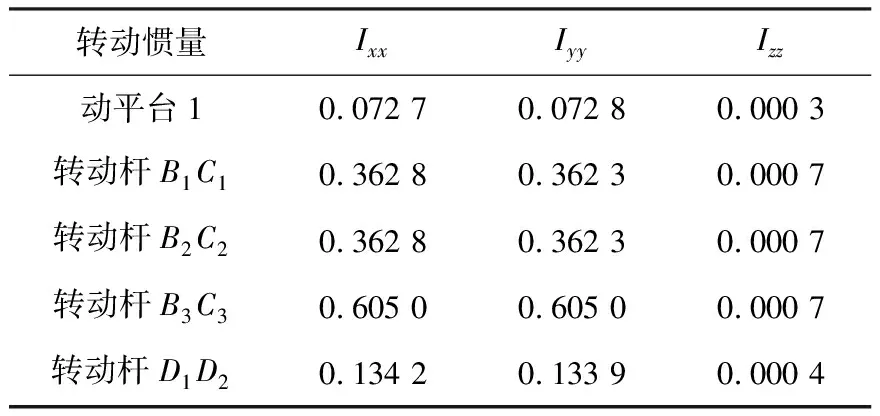
表1 2T1R并联机构中各构件的转动惯量参数

3.3.1 驱动力求解

1) 两种广义坐标下的计算

采用与文献[22]相同的运动规律(单位为mm): yA1=162.132 6+50sint，yA2=-168.926 4+50sint，yA3=98.430 0-50sint。

① 将3个驱动滑块产生的位移定义为广义坐标，即q1=(yA1,yA2,yA3)T；利用Matlab数值计算得到机构动平台空载(即oFp=0，oMp=0)的驱动力变化曲线(运算步数为1 000步)，如图3所示。

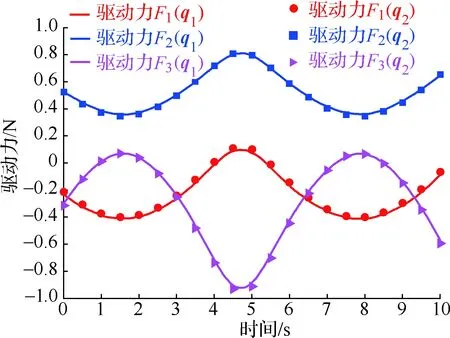
图3 Matlab计算得到驱动力变化曲线Fig.3 Driving force curve is calculated by Matlab

进一步，记录10次Matlab数值计算所用的时间，见表2中t1列所示。

表2 用Matlab计算时间t1和t2(对应广义坐标q1和q2)

② 再将动平台1在驱动滑块下产生的位移定义为广义坐标，即q2=(y,z,β)T，由于建模过程与选取q1为广义坐标相似，这里仅给出利用Matlab计算得到的机构动平台空载(即oFp=0，oMp=0)的驱动力变化曲线(运算步数为1 000步)，如图3所示，同样记录10次Matlab数值计算所用的时间，见表2中t2列。

2) 广义坐标的优选分析

由图3可知，基于虚功原理的序单开链法，在机构运动规律一致的前提下，选用不同的广义坐标，由Matlab计算得到的驱动力理论变化曲线是一致的。

由表2可知，选取q1作为广义坐标时的Matlab理论计算所用时间，比取q2作为广义坐标时的Matlab理论计算所用时间更短，响应更快。这是因为，尽管两种计算过程中，所给机构的运动时间一致且步长相同，但机构各构件速度与动平台速度点之间的关系矩阵，比建立各构件运动速度与驱动速度之间的关系矩阵更为复杂。

因此，可根据工作需求，选取合适的广义坐标进行动力学建模。建议：通过3个移动副取相同速度沿着导轨大范围移动整个机构到固定地点时，宜选取q1作为广义坐标，响应更快；而当控制动平台的精确工作轨迹时，宜选取q2作为广义坐标，这样计算过程更简便，动平台可获得更高的精度。

3) 动力学仿真计算

进一步，将虚拟样机导入到Adams中，设定好机构的运动副类型、驱动副的运动轨迹，施加沿Z轴反方向的重力，并选取仿真步长为0.01 s，仿真时间为10 s，对该2T1R虚拟样机进行动力学仿真，得到的驱动力仿真变化曲线如图4中仿真值所示。由图4可知，运用Matlab计算的理论驱动力曲线与Adams虚拟仿真驱动力结果吻合，证明了理论运算的正确性。

图4 驱动力变化曲线中的理论值与仿真值Fig.4 Theoretical value and simulation value in driving force variation curve

3.3.2 运动副D1处的支反力求解

运用Matlab计算得到2个SKC联接处D1点的理论支反力变化曲线，如图5中理论值所示；而用Adams仿真得到D1点的仿真支反力变化曲线，如图5中仿真值所示。由图5可知，基于虚功原理的序单开链法，运用Matlab计算D1点的理论支反力曲线，与Adams得到的D1点的仿真支反力曲线一致，说明了理论运算的正确性。

图5 D1点处支反力变化曲线Fig.5 The change curve of D1 reaction force

由于D1点仅能在YOZ平面内进行运动，因此，D1在X方向的支反力不能利用基于虚功原理的序单开链法求出，但可用基于Newton-Euler的序单开链法[13]求得。

3.4 与传统虚功原理法的比较分析

由虚功原理可得

(47)

式中F=(F1,F2,F3)T。其他参数与式(45)～式(46)一致，进一步简化式(47)得

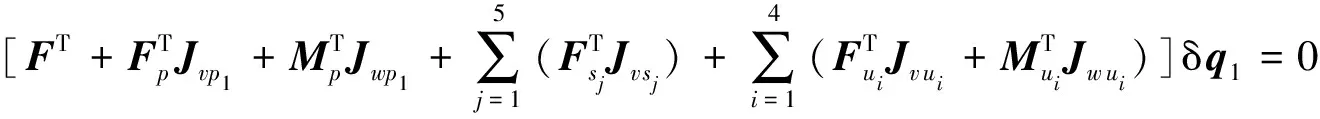
(48)

因式(48)上虚位移δq1各元素可以独立选取，因此，可得驱动力方程

(49)

采用3.3节中相同的参数和运动规律，且把q1=(yA1,yA2,yA3)T作为广义坐标，由式(48)利用Matlab计算得到机构动平台空载(即oFp=0，oMp=0)的理论驱动力变化曲线，与图3中以q1为广义坐标的曲线一致，故不单独列出。

可见，传统的虚功原理法，在建模过程中不分建模单元的先后顺序，且在动力学方程中没有体现求解任何运动副处的支反力。而基于虚功原理的序单开链法，不仅可以求出各个SKC连接处运动副的支反力(这有助于求解各SKC内其他运动副的受力情况)，而且通过SKC揭示了机构运动学与动力学之间的内在联系。

4 结 论

分析了一种新型的两平移一转动并联机构中各个杆件速度与驱动副速度之间的关系矩阵；采用基于虚功原理的序单开链法，建立该机构的动力学模型，并求解了机构的驱动力及2个SKC连接处运动副的支反力并进行了实例验证。

选取不同的广义坐标进行空间机构的逆向动力学建模与求解，其计算量不同。因此，在实际情况中需要根据工作情况，选取合适的广义坐标。移动整个机构到固定地点时，宜选取驱动副位移作为广义坐标，这样响应更快；而当控制动平台的精确工作轨迹时，宜选取动平台位移作为广义坐标，这样计算过程更简便，动平台可获得更高的精度。

基于虚功原理的序单开链法的优势之处在于，对含2个(以上)SKC的机构，既能求解驱动力，又能求出SKC连接处运动副处的支反力；当机构只有1个SKC，应选取杆、副为单元，将全部的运动副约束解除时，由Newton-Euler原理与虚功原理导出的2种动力学分析方程一致，因此，对含2个(以上)SKC的机构，选取SKC为单元，兼有Newton-Euler法和虚功原理法的优点。研究结果为该机构的设计和动力学优化奠定了基础。