数学类研究生培养质量评价的数学建模——以河南科技大学为例

李培峦 刘叶青 王海军

（河南科技大学数学与统计学院 河南洛阳 471023）

受高等教育扩招和国内外形势变化的影响，研究生数量快速增加。在研究生数量不断发展的过程中，如何保障和提升研究生培养质量越来越受到关注。

1 国内外研究现状

Edward Holdaway等提议从输入、过程、输出3个方面开展质量性的评价［1］。Jarratt Report 将研究生培养质量评价的绩效指标细化为3 个维度，并阐述了各个维度的子指标类型，以此来衡量学生质量高低［2］。

裴庆祺等引出了全面质量改善的开放系统方法，应用其构建了评估体系［3］。金云志认为应对培养质量的评价进行量化，将研究生培养质量分为5个评价等级［4］。

2 数学类研究生培养质量评价模型的建立

2.1 数学类研究生培养质量评价指标体系的建立

本文基于已有研究，建立了如表1所示的由5个一级指标和13 个二级指标构成的数学类研究生培养质量评价指标体系［6］。

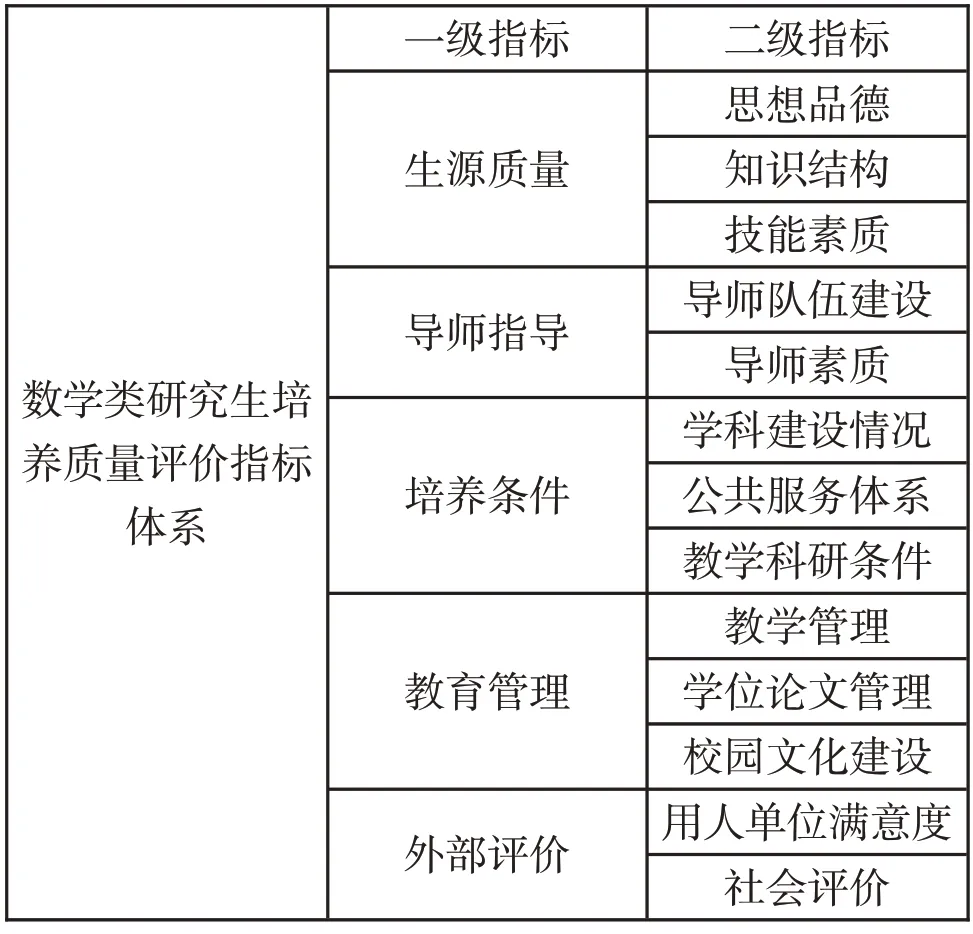
表1 数学类研究生培养质量评价指标体系

2.2 数学类研究生培养质量评价指标权重的确定

各评价指标对总目标影响程度不同，即所占权重不同。而合适的权重确定方法很重要，故本文选择在现实生活中应用十分广泛的层次分析法，其具体步骤如下。

（1）建立层次结构模型。

（2）构造判断矩阵A，A中元素表示某层某个因素相对于上层某个因素的重要程度。

（3）层次单排序，通过对矩阵A进行一致性检验确定其不一致程度，若不一致程度在允许范围内，则通过检验，计算出的特征向量归一化后即为权重向量W，W的分量即为相应元素单排序的结果。

（4）一致性检验，计算一致性比率CR，如果CR＜0.1，则可认为判断矩阵的不一致程度在容许范围内，通过一致性检验；否则修正判断矩阵，直至通过检验。

（5）层次总排序及其一致性检验，计算某一层次所有因素对于最高层的权重，自上而下合成单准则下权重。若b1，b2，…，bm是B1，B2，…，Bm对总目标的权重，c1j，c2j，…，cnj是C1，C2，…，Cn对于Bj的权重（当Ci与Bj无关联时，cij=0，j=1，2，…，m），则C层的层次总排序，即对总目标权重为：

同样进行一致性检验，C层层次总排序一致性比率为：

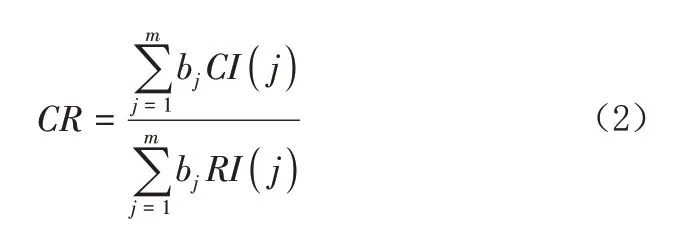
若CR＜0.1，则通过检验，否则修正判断矩阵或重新建立模型。

2.3 基于模糊综合评判的研究生培养质量评价模型的建立

根据上文建立的二级评价指标体系，建立研究生培养质量的二级模糊综合评判模型，具体步骤如下。

（1）确定评价因素集，也称指标体系，用U={u1，u2，…，um}表示。

（2）确定评语集。评语集用V={v1，v2，…，vn}表示，往往对应3～5个等级。

注意隶属度要归一化以消除量纲的影响，进而得到单因素评判矩阵：

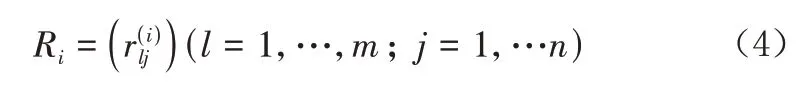
（5）一级模糊综合评判，对每个Ui进行综合评判，即将其权重向量Wi与单因素评判矩阵Ri加权平均，得一级模糊综合评判向量Fi：

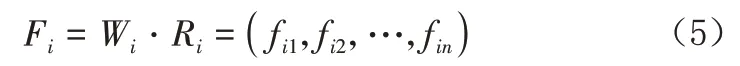
（6）二级模糊综合评判，视每个Ui为一个因素，则U={U1，U2，…，Uk}是单因素集，则R为：

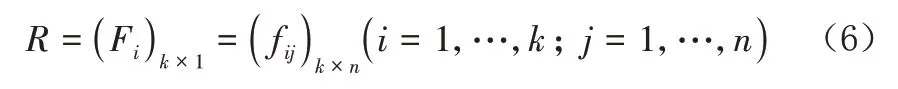
将其权重向量W0与单因素评判矩阵R进行模糊合成，则可得二级模糊综合评判向量为［19］：

（7）对模糊综合评判向量进行分析处理，本文选择加权平均原则分析处理模糊综合评判向量F，具体方法为：量化评语集中的各评价等级，得到模糊评判评语量化集S=(S1，S2，…，Sn)T，然后用二级模糊综合评判向量对S的加权平均值作为综合得分E，即：

各一级指标的综合得分为：

3 数学类研究生培养质量评价模型的实证分析

3.1 数据说明

本文用调查问卷确定隶属度，河南科技大学数学研究生及导师对12 个二级指标进行选择。调查共回收有效问卷50 份。用SPSS 得测度变量的Cronbach α系数为0.923 ＞0.8，说明问卷数据信度较高。用人单位满意度二级指标的评价数据来自于学科评估时用人单位填写的相关调查表。

3.2 模型的实证分析

3.2.1 利用AHP确定各评价指标权重

（1）建立层次结构模型。

根据表1可建立如图1所示的层次结构模型。

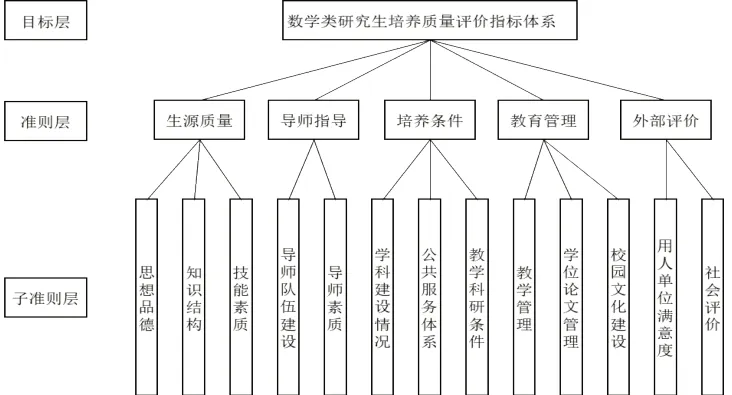
图1 层次结构模型

（2）构造判断矩阵。

目标层为O，准则层为B，子准则层为C，并进行编号。记O层对B层的判断矩阵为A0，B层对C层的判断矩阵分别为A1，A2，A3，A4，A5。则根据有关专家的意见，可得A0，A1，A2，A3，A4，A5，其中A0见表2。

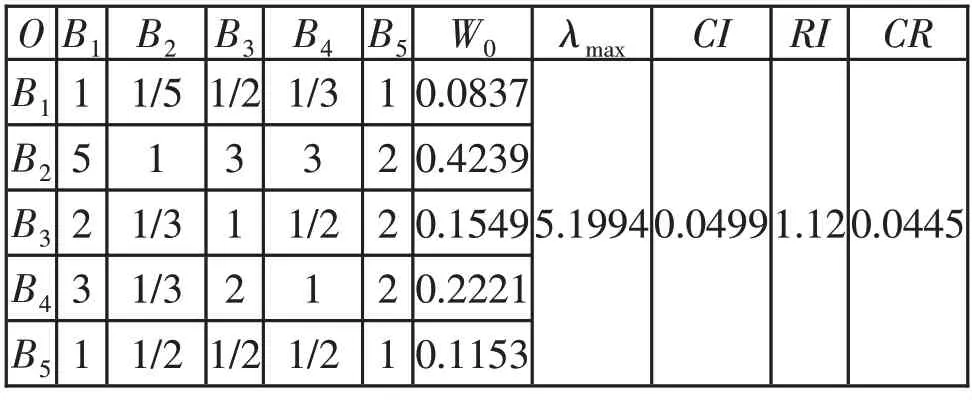
表2 数学类研究生培养质量指标判断矩阵A0

（3）层次单排序及其一致性检验。

借助软件，计算出所有所需数据，其中判断矩阵A0，CR＜0.1，通过一致性检验，其余CR皆小于0.1，全部通过一致性检验。

（4）层次总排序及其一致性检验。

C层的层次总排序由前面的结果和式（1）计算得出，结果汇总如表 3 所示。由式（2）得层次总排序一致性比率CR=0.0117 ＜0.1，一致性检验通过。

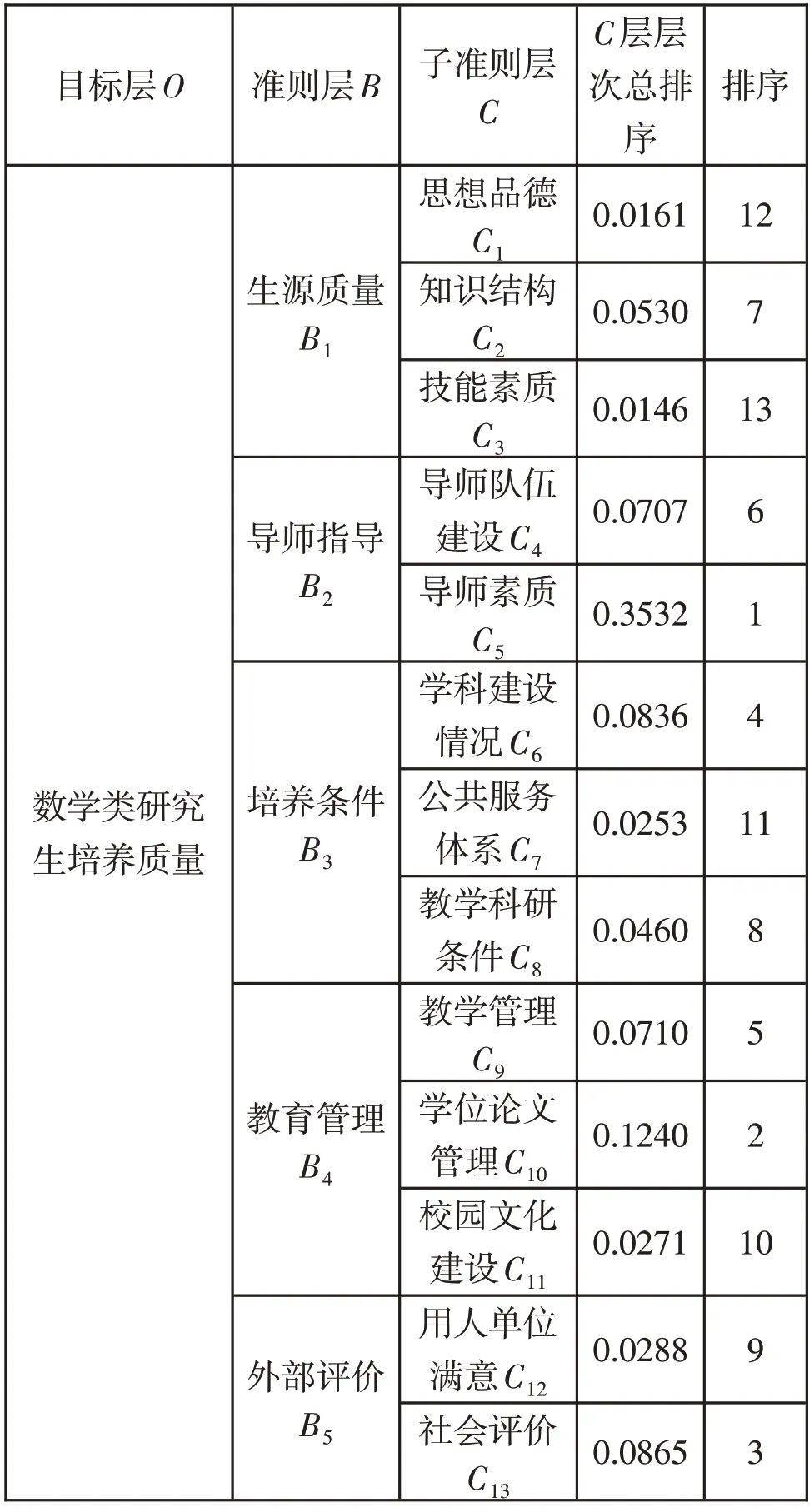
表3 层次总排序结果汇总

3.2.2 二级模糊综合评判模型的实证分析

（1）由表1数学类研究生培养质量评价指标体系，可得评价因素集为：

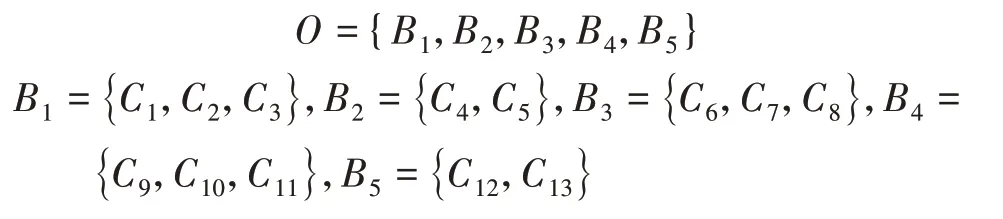
（2）评语集V={V1，V2，V3，V4，V5}={优秀，良好，一般，较差，很差}，把0～100 划分成5 个范围分别对应评语集的5 个等级，取分值范围的中位数构造模糊评判评语量化集（或评价尺度）S，如表4 所示，则S=(95，84.5，74.5，64.5，29.5)T。

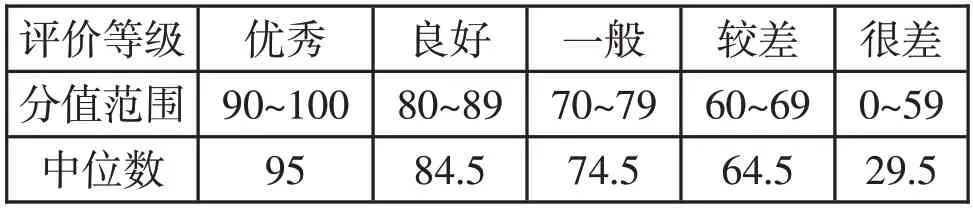
表4 分值范围表

（3）前文采用AHP 已得到各级指标的权重向量，分别为：

（4）对结果进行汇总如表5所示，对隶属度归一化后得到R1～R5。

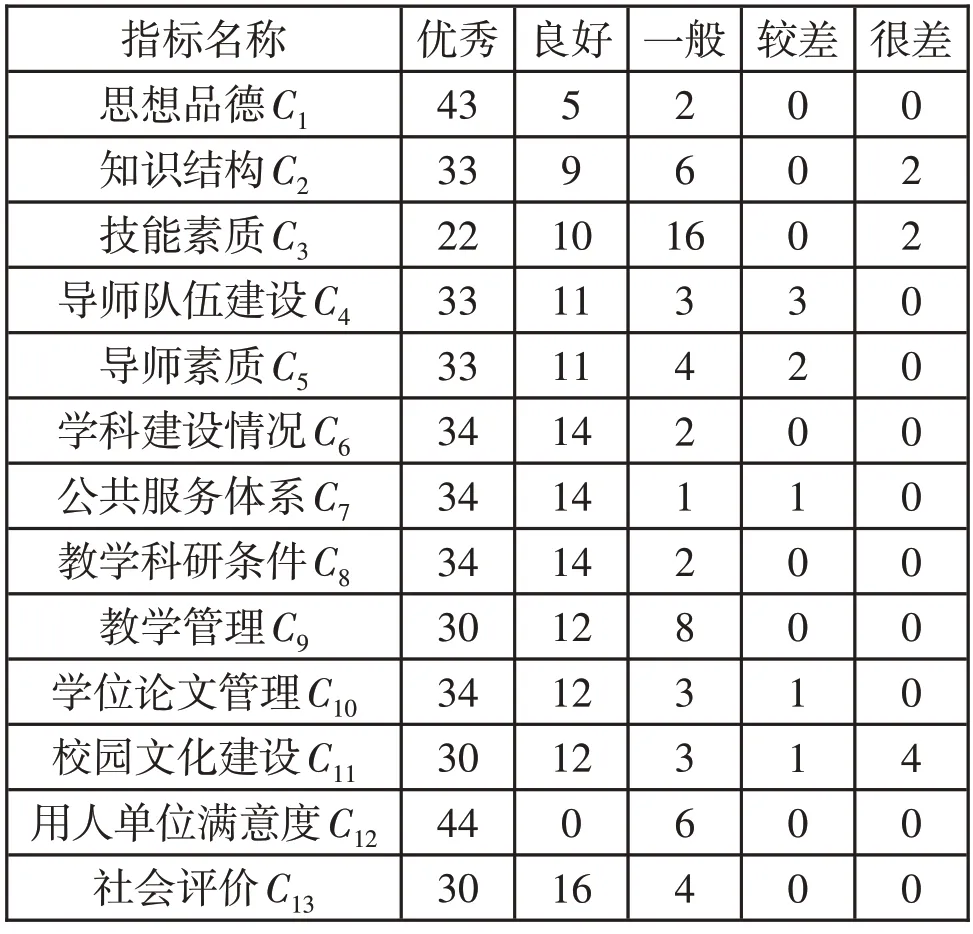
表5 评价结果汇总表

（5）由式（5）得一级模糊综合评判向量为F1，F2，F3，F4，F5。

（6）由式（6）得O的单因素评判矩阵为：

得二级模糊评判向量为：

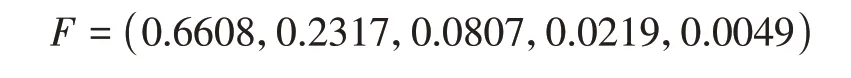
（7）综合得分分别为89.9171，88.2570，89.7967，91.2073，89.5405，90.6350。

3.2.3 模糊综合评判结果分析

将上面计算出的各层指标的综合得分，汇总如下，见表6、表7。

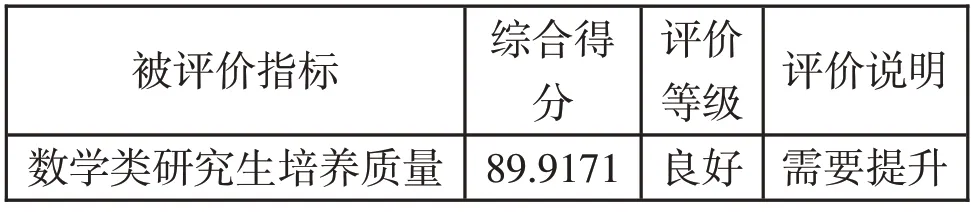
表6 研究生培养质量综合评价结果分析

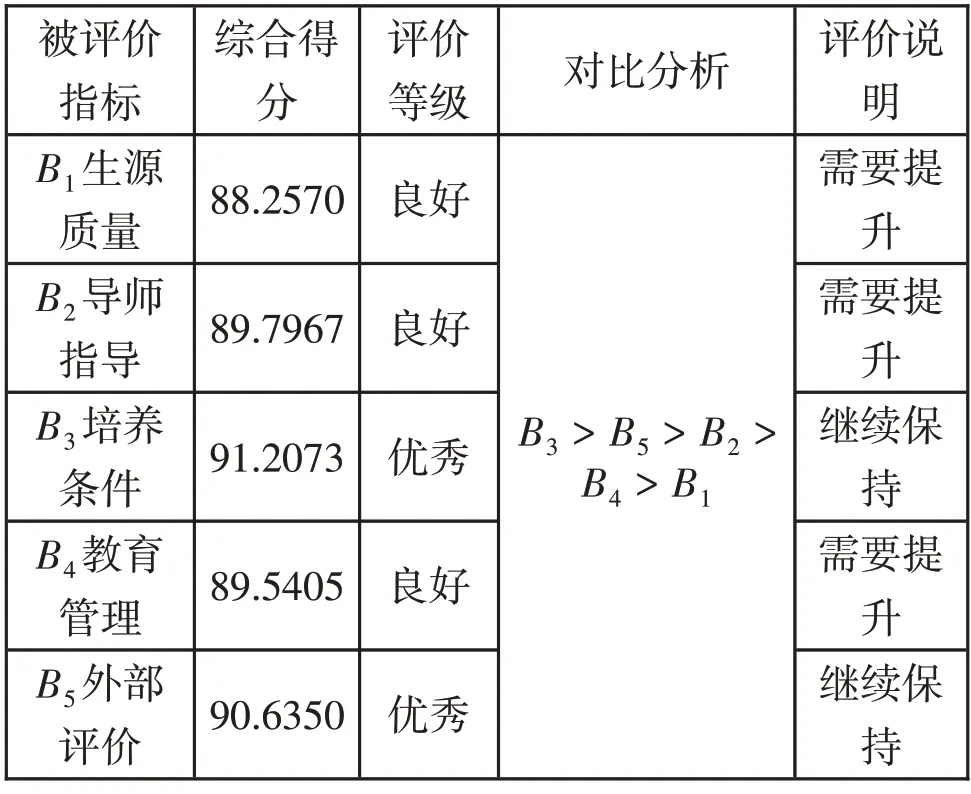
表7 准则层一级指标综合评价结果分析

结果分析：河南科技大学数学类研究生培养质量综合得分为89.9171，等级为良好，可进一步提升。培养条件和外部评价综合得分较高，等级为优秀，应继续保持。生源质量、导师指导和教育管理评价等级为良好，需进一步提升。