发散冷却和前缘槽缝射流作用下涡轮静叶端壁流动结构的研究
孙添一,李志刚,李军
(西安交通大学叶轮机械研究所,710049,西安)
地面燃机涡轮进口温度已经达到1 600 ℃,航空发动机甚至更高,已经超过燃气透平热端部件材料的耐温极限。同时,为了降低污染排放而采用的高效预混干低NOx燃烧室设计,使得燃烧室出口截面上的温度分布更加均匀,进一步增加了端壁处的热负荷[1]。为保证燃气涡轮的寿命与可靠性,对涡轮静叶叶栅端壁气热性能开展研究显得尤为重要[2]。
燃气涡轮第一级静叶端壁受到高湍流度燃气与各种复杂二次流结构的影响,热负荷高,需要对其进行有效冷却。燃烧室壁面冷却气流量大,影响燃烧室出口温度、速度分布;同时,燃烧室壁面发散冷却和前缘槽缝射流冷却的综合作用,将进一步影响下游静叶叶栅和端壁流动与气膜冷却覆盖特性[3-4]。因此,开展燃烧室壁面发散冷却和前缘槽缝射流冷却综合作用对涡轮静叶叶栅端壁流动结构影响的研究具有重要意义。
针对涡轮叶栅流动结构与冷却特性,研究人员重点关注冷却气对端壁附近二次流结构的影响。Goldstein等实验研究了涡轮叶栅的三维流动结构,研究表明初始马蹄涡、通道涡以及角区涡对是对端壁气热特性产生显著影响的主要二次流结构[5]。Cui等数值研究了高负荷低压涡轮的端壁流动特性,研究发现来流湍流边界层、尾迹与二次流是叶栅总压损失的主要来源,而层流边界层引起的气动损失较小[6]。Zhang等数值研究了槽缝射流旋流比与密度比对涡轮静叶冷却特性的影响,结果表明密度比较小时,旋流比降低会恶化端壁冷却效果,而密度比较大时端壁冷却有效度随旋流比减小先降低后增高,同时旋流比与密度比变化会影响叶片泛冷却效果[7]。Shiau等实验研究了叶栅通道气膜孔布置方式及叶片前缘气膜孔射流角对冷却特性与流动结构的影响,指出叶片前缘气膜孔射流角增大时,冷却效果变差,且叶栅通道内气膜孔的冷却效果主要取决于叶片前缘冷却气能否有效抑制马蹄涡等二次流结构[8]。Leonetti等研究了两种稀释流冷却孔布置方式对涡轮叶栅流场的影响,发现高动量的稀释流冷却气使得下游静叶叶栅进口速度、温度分布极不均匀[9]。Holgate等对燃烧室稀释流冷却与叶片前缘气膜冷却共同作用下的端壁流动、冷却特性实验研究发现,滞止区气膜冷却气与稀释流间的干涉作用越强,冷却效果越好[10]。Murihead等对比了不同数值方法对燃烧室稀释流作用下的涡轮叶栅气热特性预测结果,研究表明DDES模型计算得到的燃烧室出口截面温度分布比RANS模型更加均匀,因为其预测了更强烈的稀释流间的掺混作用,从而显著影响了叶栅通道内流场的预测结果[11]。
发散冷却应用于燃烧室壁面冷却[12]。Sacchi等实验研究了发散冷却对高压涡轮叶栅端壁气热性能的影响,研究表明发散冷却气对端壁边界层的能量补充削弱了通道涡与马蹄涡压力面侧分支的强度,叶片前缘上游区域的冷却效果几乎不受吹风比影响,而叶栅喉部的绝热冷却有效度则对冷却气流量极为敏感[13-14]。Nawathe等实验研究了发散冷却、前缘气膜冷却作用下叶栅通道内流动情况,发现冲击涡强度仅和发散冷却气流量有关,来自燃烧室冷却结构的冷却气流使端壁横流对叶栅通道内流动的影响更加显著[15]。Alqefl研究了燃烧室冷却气存在时上游槽缝射流对叶片端壁的影响,研究表明槽缝射流质量流量增加会使通道涡引起的总压损失增加,并在其附近形成另一个旋向相反的涡,马蹄涡压力面侧分支会加强冷却气与主流的掺混,对冷却效果影响显著[16]。
燃烧室壁面发散冷却和前缘槽缝射流冷却对下游涡轮静叶端壁流场型态的影响研究需要深化,为端壁冷却设计提供基础。本文研究了考虑燃烧室壁面发散冷却和槽缝射流冷却综合作用下涡轮静叶端壁的流动结构,可为涡轮静叶端壁气热性能分析和气膜冷却布局设计提供参考。
1 计算模型和数值方法
1.1 计算模型
图1给出了包含燃烧室壁面发散冷却和前缘槽缝射流冷却结构的涡轮静叶叶栅和端壁结构图,燃烧室壁面的发散冷却结构包含6排交错排列的144个圆柱形发散孔,槽缝出口中心线位于叶片前缘上游0.2倍轴向弦长处。表1列出了模型几何参数[3]。

图1 发散冷却和槽缝射流与静叶端壁的计算模型[3]Fig.1 Computational model of vane endwall, effusion cooling and slot jet[3]
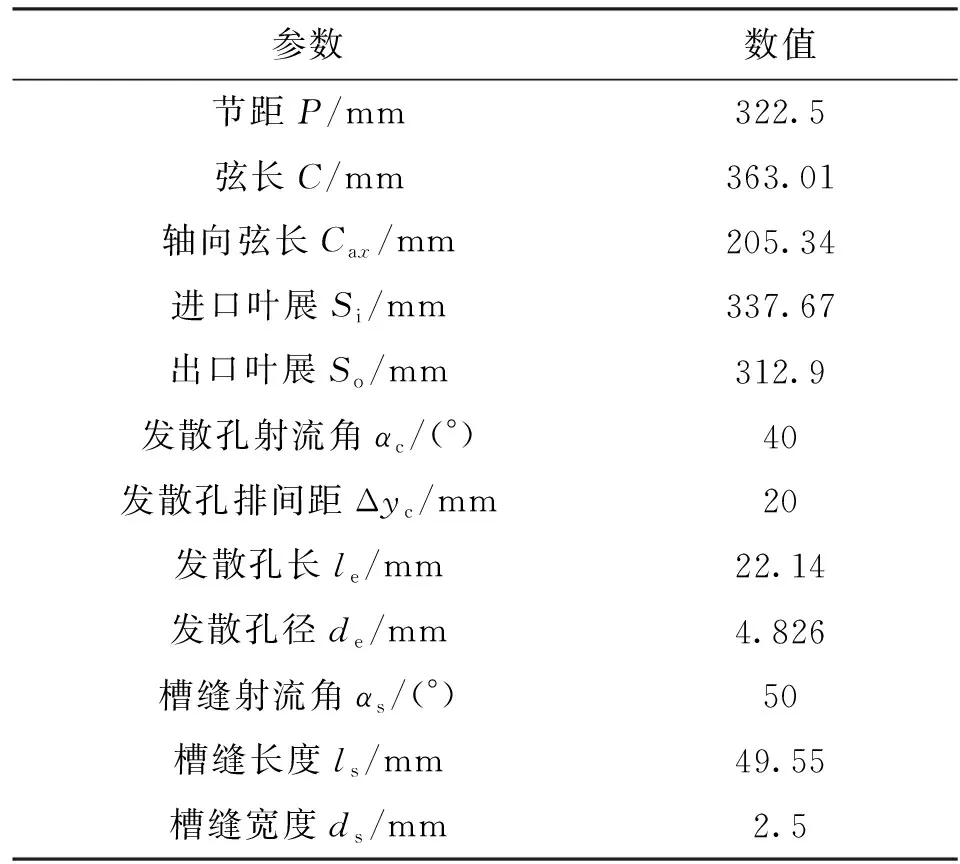
表1 计算模型几何参数[3]Table 1 Geometric parameters of the computational model
1.2 数值方法与验证
采用ICEM CFD对包括发散冷却和前缘槽缝射流冷却结构的涡轮静叶生成结构化计算网格。为保证网格质量,在叶片附近区域与气膜孔、槽缝内均生成O型网格并对近壁面区域网格进行加密。图2给出了计算模型的网格图。
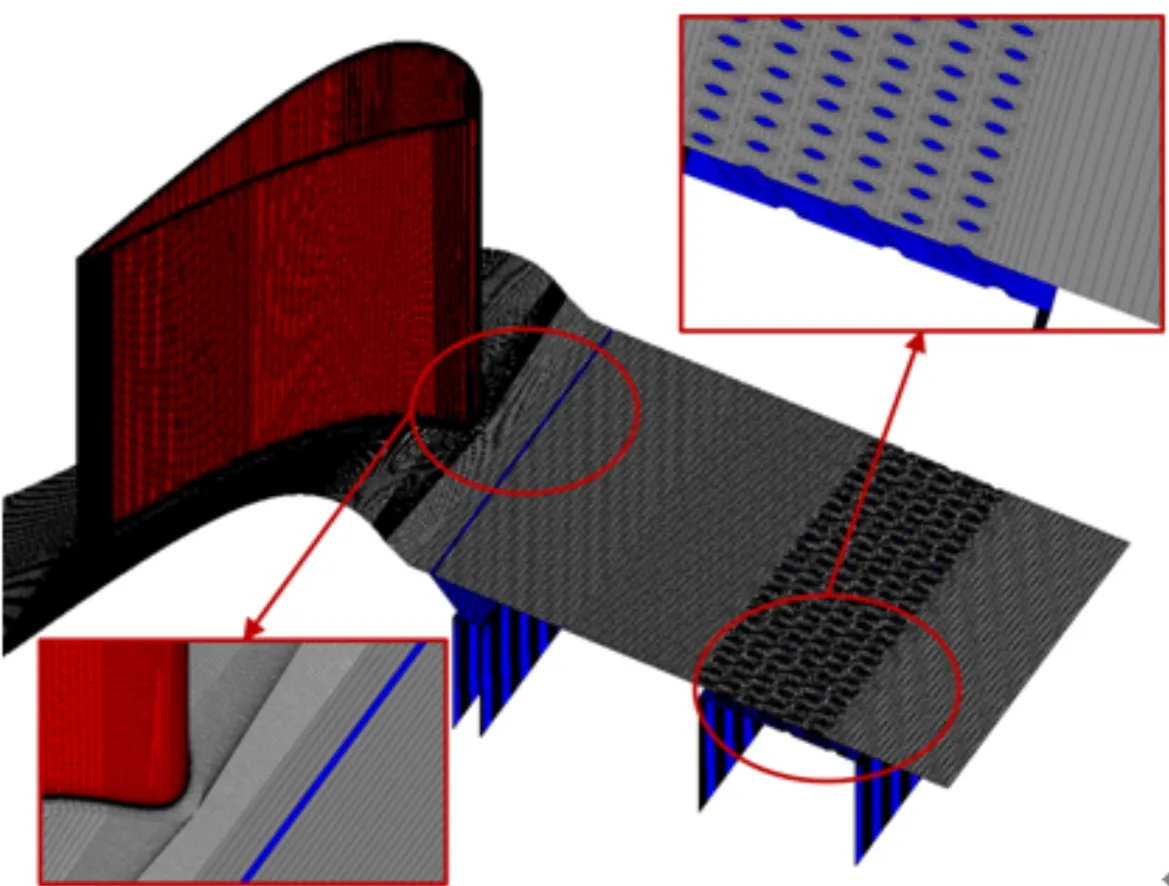
图2 发散冷却和槽缝射流与静叶端壁的计算网格Fig.2 Computational mesh of vane endwall, effusion cooling and slot jet
采用ANSYS CFX 18.0对SSTk-ω湍流模型和γ-θ转捩模型进行数值求解。壁面采用绝热无滑移壁面边界条件。求解过程中,当控制方程均方根残差小于10-5且进、出流量基本平衡时,认为数值求解已经收敛。表2给出了计算的边界条件,主流与冷却气的温度设置参考文献[17],该条件可以保证冷却气与主流的密度比RD=1.75,与真实燃机中的密度比相近。

表2 计算边界条件Table 2 Computational boundary conditions
表3与图3分别给出了特征截面(位于叶片前缘上游1倍轴向弦长处)雷诺数和横向端壁平均壁面温度的网格无关性验证,采用5套计算网格进行了网格无关性验证,发散冷却气腔室进口和槽缝射流冷却气腔室进口总压分别设置为107.422 5 kPa与106.127 6 kPa,选取特征截面雷诺数与横向平均绝热冷却有效度为评价指标。由表3可知,网格数为1 409万与1 656万的两套网格,特征截面处雷诺数相差不到0.2%。由图3可知,在叶栅通道中上游位置,1 409万与1 656万网格的计算结果几乎相同,下游处1 409万网格计算所得壁面温度略高。综合考虑计算精度与所占用计算资源,本文采用1 409万网格进行数值计算。
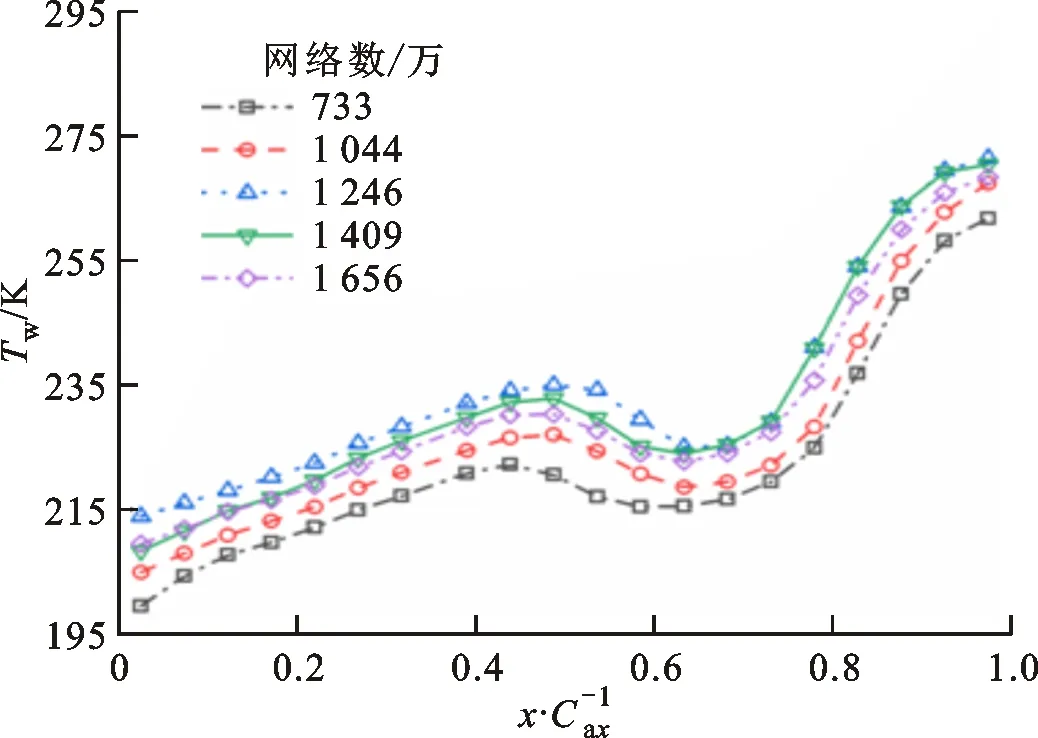
图3 不同网格数横向端壁平均壁面温度Fig.3 Laterally averaged end wall temperature for different grid-node numbers

表3 不同网格数特征截面雷诺数Table 3 Reynold number at specific profile with different grid-node number
对明尼苏达大学的发散冷却直列叶栅实验模型,采用不同湍流模型进行数值计算以验证数值方法可靠性。图4给出了数值计算和实验数据的比较。数值计算的湍流模型分别是SSTk-ω结合γ-θ转捩模型与k-ε模型。如图4a所示,SST+γ-θ模型预测得到的绝热冷却有效度分布与实验数据吻合良好,捕捉到压力面侧上游与尾缘处以及喉部吸力面侧的低冷却区域,而k-ε模型预测结果中喉部下游冷却有效度明显偏低。由图4b可知,两种湍流模型对叶型静压系数分布预测结果均与实验数据吻合良好,而SST+γ-θ模型对吸力面静压系数分布预测偏差较小,因此本文采用SST+γ-θ模型。
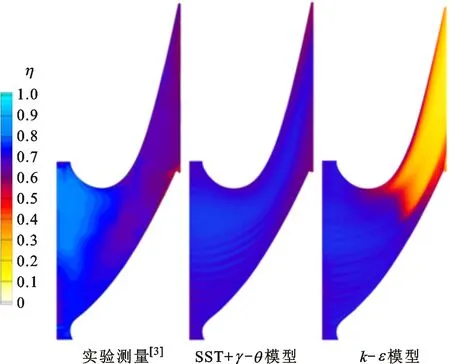
(a)绝热冷却有效度η分布

(b)叶型静压系数Cp分布图4 数值冷却有效度及静压系数分布与实验数据[3]比较Fig.4 Comparison of numerical cooling effectiveness and static pressure coefficient with experimental data
2 结果分析与讨论
冷却气与主流质量流量比为
(1)
式中:Qc为冷却气质量流量;Qm为主流质量流量。
表4列出了不同发散冷却气质量流量比的4种计算工况。通过对比分析不同发散冷却气质量流量下涡轮静叶端壁气动和传热冷却特性,分析发散冷却和前缘槽缝射流冷却下的涡轮静叶端壁气热性能变化特性。

表4 不同发散冷却气质量流量比的工况Table 4 Conditions with different effusion cooling mass flow rates
2.1 端壁二次流
为了更清楚地说明发散冷却与槽缝射流综合作用下的造型端壁附近二次流结构,首先以上端壁代表对该主流条件下无冷却气的平直端壁,并对其附近二次流进行分析。
图5给出了上端壁附近与壁面距离2.5 mm的等值面处涡量Ω分布,其中红色代表由进口朝向出口、旋向为顺时针的正向涡量,蓝色则代表逆时针旋向。图6给出了上端壁附近二次流三维流线图。参考文献[18],气流在叶片前缘发生滞止后向端壁卷起并沿叶片两侧发展,形成旋向相反的马蹄涡压力面侧分支(HV-PS)与吸力面侧分支(HV-SS)。HV-PS在叶栅通道内压力梯度的作用下向吸力面侧发展,形成通道涡(PV),而HV-SS在吸力面角区发展至喉部后,由于叶片折转过于强烈,从叶表脱离,如图6中红色流线所示。如图5所示,从喉部截面开始,吸力面角区附近出现旋向相反的两个涡结构,文献[5]将其命名为吸力面角区涡对(SSCVs)。如图6所示,端壁边界层内流体在压力梯度作用下向吸力面折转,形成端壁横流。端壁横流抵达吸力面后沿叶表向上卷起,并进入吸力面角区涡对间的缝隙,因此在图6靠近下游的截面处,端壁横流流线恰好处于两个涡量符号相反的区域交界处。

图5 上端壁附近涡量分布Fig.5 Vorticity distribution near upper endwall
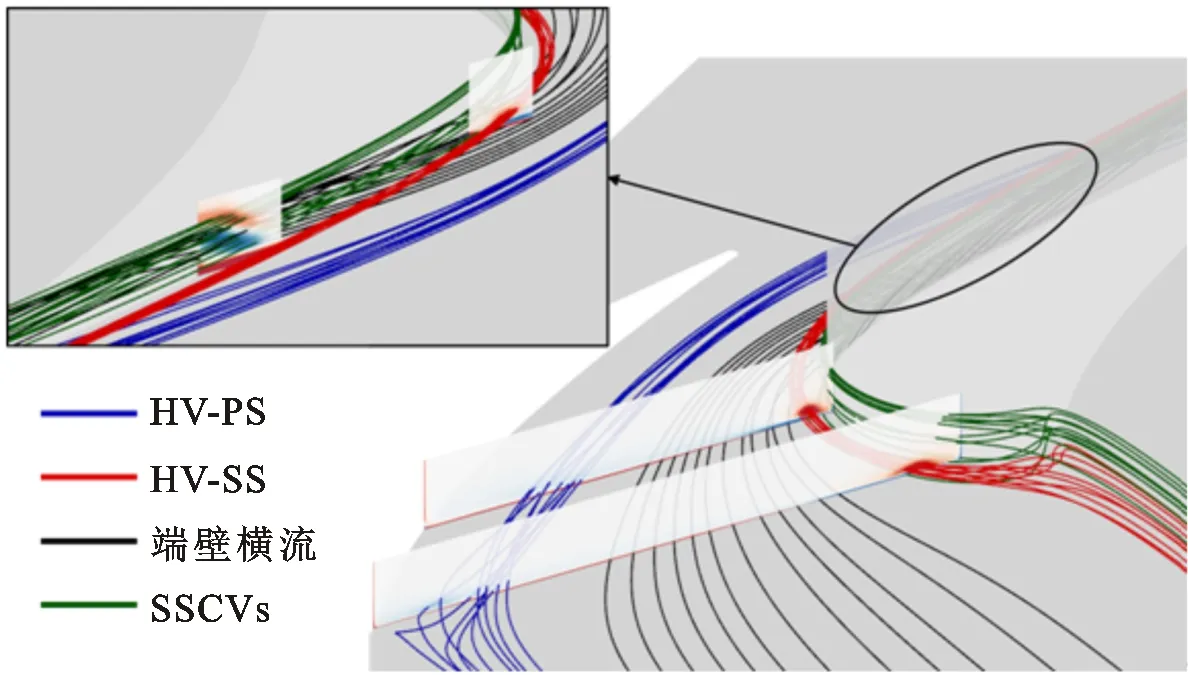
图6 上端壁附近二次流三维流线图Fig.6 Three-dimensional streamlines of secondary flow near upper endwall
图7对比了各工况下端壁附近与壁面距离2.5 mm的等值面处涡量分布。图8以工况1与工况4为例,给出了有、无发散冷却结构时下端壁附近的二次流三维流线图。由图7a与图8a可见,相比无冷却气的平直上端壁,槽缝射流与端壁造型使下端壁附近流速增加,气流抵抗叶栅通道折转的能力增强,通道涡始终在压力面附近发展,至尾缘下游处才开始转向吸力面侧。此外,部分槽缝射流冷却气由于流速较高,保持轴向流动,会在压力面角区被卷吸进入通道涡,如图8a中蓝色流线所示。

(a)工况1

(b)工况2

(c)工况3

(d)工况4图7 各工况下端壁附近涡量分布Fig.7 Vorticity distributions near hub endwall in different working conditions
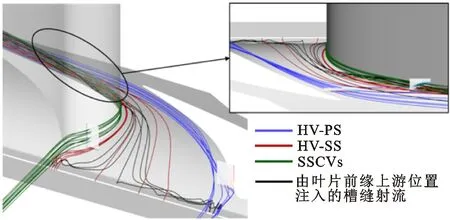
(a)工况1
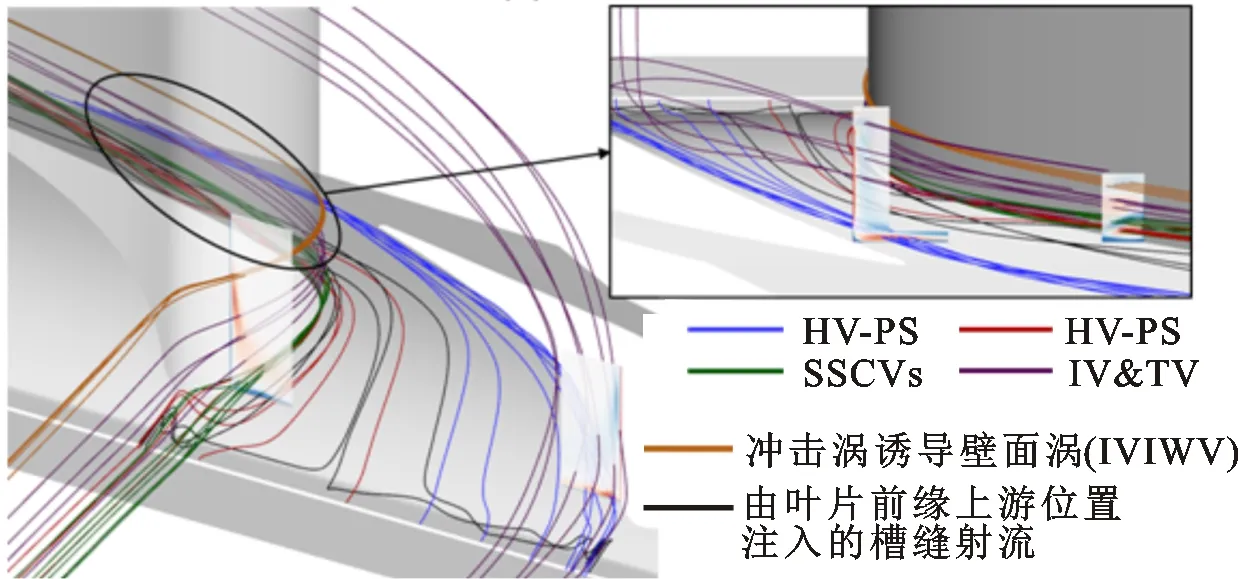
(b)工况4图8 有、无发散冷却时下端壁附近二次流三维流线图Fig.8 Three-dimensional streamlines of secondary flow near hub endwall with and without effusion cooling
槽缝射流对马蹄涡的影响也较为显著。如图8a所示,相比于主流边界层,动量更高的槽缝射流冷却气滞止现象更加明显,大量冷却气进入马蹄涡。由叶栅通道中部位置射入的冷却气也会在端壁横流的作用下转向吸力面侧,并被卷吸进入马蹄涡吸力面侧分支,如图8a中红色流线所示。此外,部分来自于叶片前缘上游位置的槽缝射流冷却气会在端壁造型开始位置形成回流涡,向两侧横向流动并在叶栅通道中央静压较低的位置进入。这部分冷却气在回流涡中损失大量能量,因此会更容易向吸力面折转,如图8a中黑色流线所示。
存在发散冷却气时,叶片前缘附近马蹄涡上方出现了与马蹄涡旋向相反的涡量区,如图7b~7d所示,即为冲击涡(IV)。其形成机理与马蹄涡类似,是由高总压流体向低总压方向卷起导致的。图9给出了叶栅通道进口截面横向平均总压系数沿叶展方向的分布情况。总压系数定义为
(2)


图9 进口截面横向平均总压系数沿叶展方向分布Fig.9 Spanwise distributions of laterally averaged total pressure coefficient on inlet profile
由图9可见,发散冷却气质量流量比由5%增加至7%时,横向平均总压峰值升高了3.7%,即M越高总压峰值越高,冲击涡也越强。在压力面侧,IV-PS在叶表上洗的范围逐渐增大,对M最高的工况4,还会在其上部分离出一个较小的三次涡(TV)结构[3],如图7d与图8b所示。在吸力面侧,较小的M会使起始强度较低的IV-SS在叶栅中下游位置便耗散殆尽,如图7b所示。另外,在IV-SS上方出现了与其旋向相反的涡结构,其起始位置与SSCVs相同,是冲击涡影响叶表吸力面边界层流动导致的,如图8b黄色流线所示,将其命名为冲击涡诱导壁面涡(IVIWV)。与冲击涡相同,IVIWV随M增加而增强,而SSCVs受发散冷却气质量流量比影响趋势相反。
各种二次流结构是静叶叶栅中总压损失的主要来源之一,图10给出了4种工况的总压损失系数分布。总压损失系数定义为
(3)
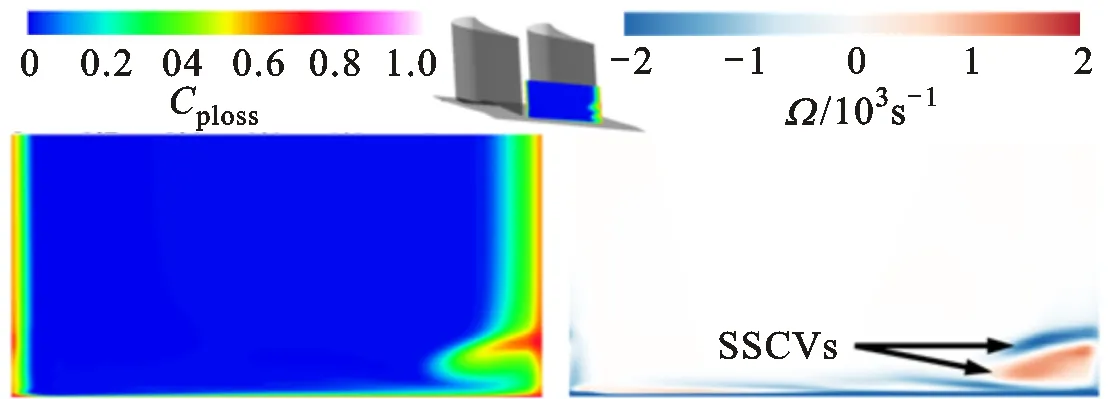
(a)工况1

(b)工况2
(c)工况3
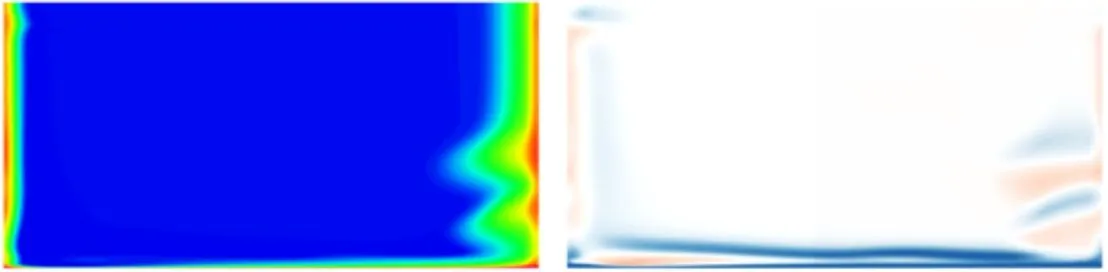
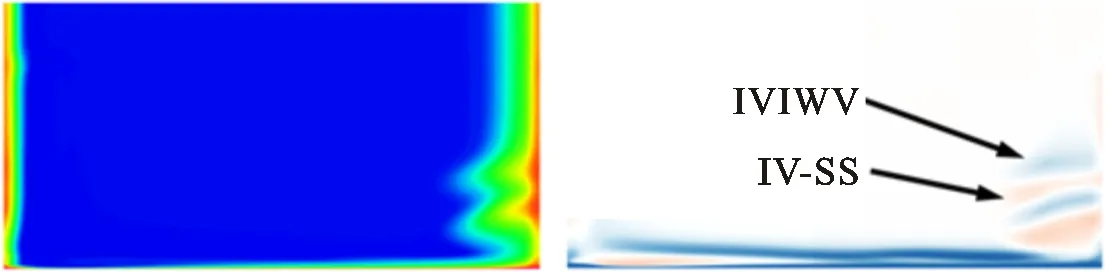
(d)工况4图10 出口截面总压损失系数与涡量分布Fig.10 Total pressure loss coefficient and vorticity distributions on outlet profile
式中pto为出口截面某位置总压。图10给出了叶栅通道出口截面处的总压损失系数与涡量分布情况。如图可见,除了壁面附近的型面损失区之外,吸力面附近还出现了额外的高总压损失区。对无发散冷却的工况1与发散冷却流量较小的工况2,吸力面端壁附近出现高总压损失区域,而对发散冷却气流量较高的工况3与工况4,原区域上方出现了新的高损失区。对比出口截面涡量云图可见,以上高损失区域位置对应SSCVs的两个对转涡交界位置与IV-SS和IVIWV的交界位置。无发散冷却时,无冲击涡与壁面涡,而发散冷却流量较小的工况2,IV-SS与IVIWV强度较弱,无法发展至叶栅出口,因此图10a与图10b中仅出现一个高总压损失区域。由此可见,引起总压损失的因素并非某一单一涡结构,而是两个旋向相反的涡交界位置剧烈的摩擦与耗散。
图11给出了叶栅出口截面横向平均总压损失系数沿叶展方向的分布。如图可见,发散冷却气质量流量比增加时,下方高总压损失区总压损失降低,上方高总压损失区总压损失升高且向中间叶展位置移动。这是因为发散冷却气流量增加会削弱SSCVs并增强冲击涡及其诱导壁面涡,与前面得到的讨论结果相符。叶栅出口平均总压损失系数如表5所示。可见质量流量比为5%的发散冷却气会抑制吸力面角区涡对,减少总压损失,而M由5%升高至7%时,IV-SS与IVIWV增强,平均总压损失增加4.5%。

表5 叶栅出口平均总压损失系数Table 5 Total pressure loss coefficient at the outlet
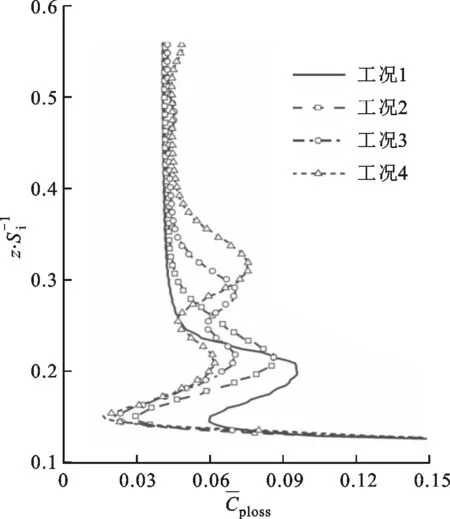
图11 出口截面横向平均总压损失系数沿叶展方向分布Fig.11 Spanwise distributions of laterally averaged total pressure loss coefficient on outlet profile
2.2 冷却气流动
叶栅通道内各种二次流结构会影响冷却气流动,且来源于两种冷却结构的冷却气间也会发生相互作用,改变叶栅通道壁面的冷却特性。图12给出了叶栅通道端壁与各截面绝热冷却有效度分布。绝热冷却有效度定义为
(4)
式中:Tr为主流恢复温度;Tc为冷却气温度。如图12a所示,在仅有槽缝射流作用时,压力面侧、叶片前缘与吸力面上游角区位置端壁不能得到冷却,而在有发散冷却气注入时,整个端壁均可以得到充分的冷却气覆盖。需要注意的是,绝热冷却有效度没有考虑冷却气射入以及流动过程中与壁面换热导致的温度变化(尤其是发散冷却气),因此不能代表实际冷却效果,而仅代表冷却气的分布情况。发散冷却气质量流量比越高,在上游位置(x=-0.15Cax截面)形成的气膜越厚,出口位置(x=0.97Cax截面)吸力面附近形成的冷却气团越明显,结合前文对二次流结构的讨论,该位置的冷却气聚集现象与吸力面角区涡对有关。纵向分析各截面的温度分布发现,气膜厚度会随着其在叶栅通道中的流动迅速减薄。这一方面是因为冷却气在压力面侧会逐渐沿叶表向中间叶展方向流动,在吸力面侧会发生上述在角区位置的聚集,使覆盖在端壁的冷却气减少;另一方面是因为气膜在流动过程中与主流相互掺混,并发生剧烈的耗散。
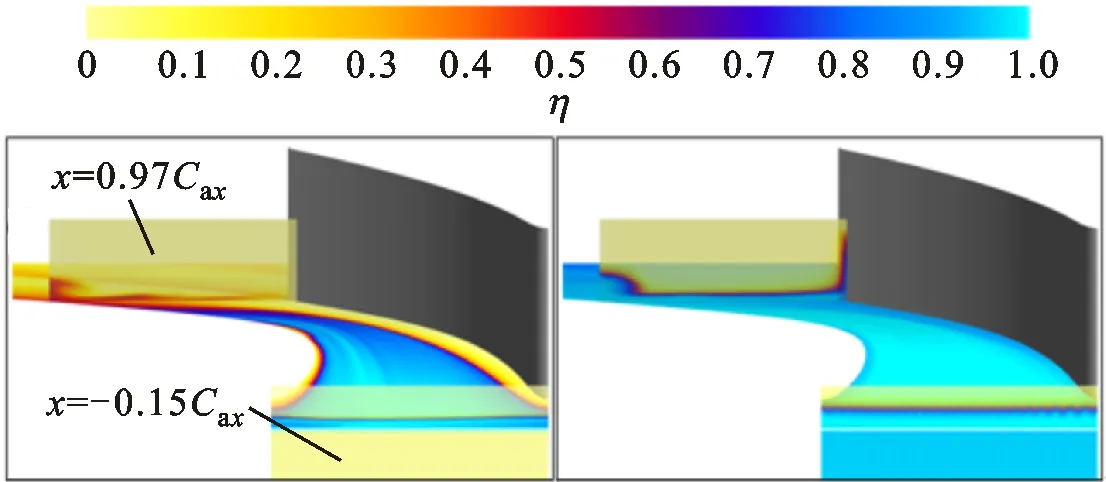
(a)工况1 (b)工况2
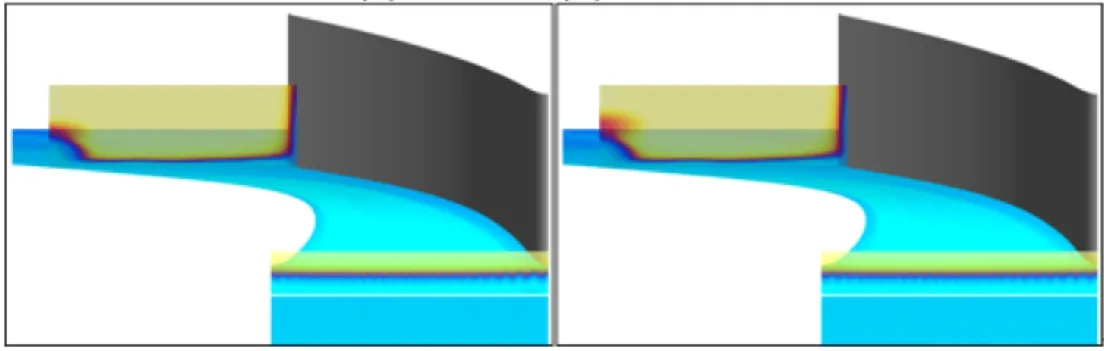
(c)工况3 (d)工况4图12 叶栅通道端壁与各截面绝热冷却有效度分布Fig.12 Adiabatic cooling effectiveness distributions on hub endwall and each profile
冲击涡的旋向与马蹄涡相反,导致其会卷吸大量发散冷却气沿叶片表面上吸,尤其是强度不断增加的IV-PS,会对冷却气发展趋势产生显著影响。图13给出了喉部截面温度场与平面流线图。在没有发散冷却时,如图13a所示,不存在IV,证实发散冷却气形成的高总压区是冲击涡形成的必要条件。发散冷却气质量流量比升高会使冲击涡强度增加并沿叶展方向明显拉长。冲击涡会使冷却气沿压力面向上覆盖,在叶表形成冷却气膜。在发散冷却气质量流量比很高时,如图13d中工况4(M=7%),冲击涡沿叶展方向伸长并分裂形成三次涡,该涡旋向与冲击涡相同,使冷却气进一步向叶顶方向覆盖,并在气膜最上部形成一个冷却气团。
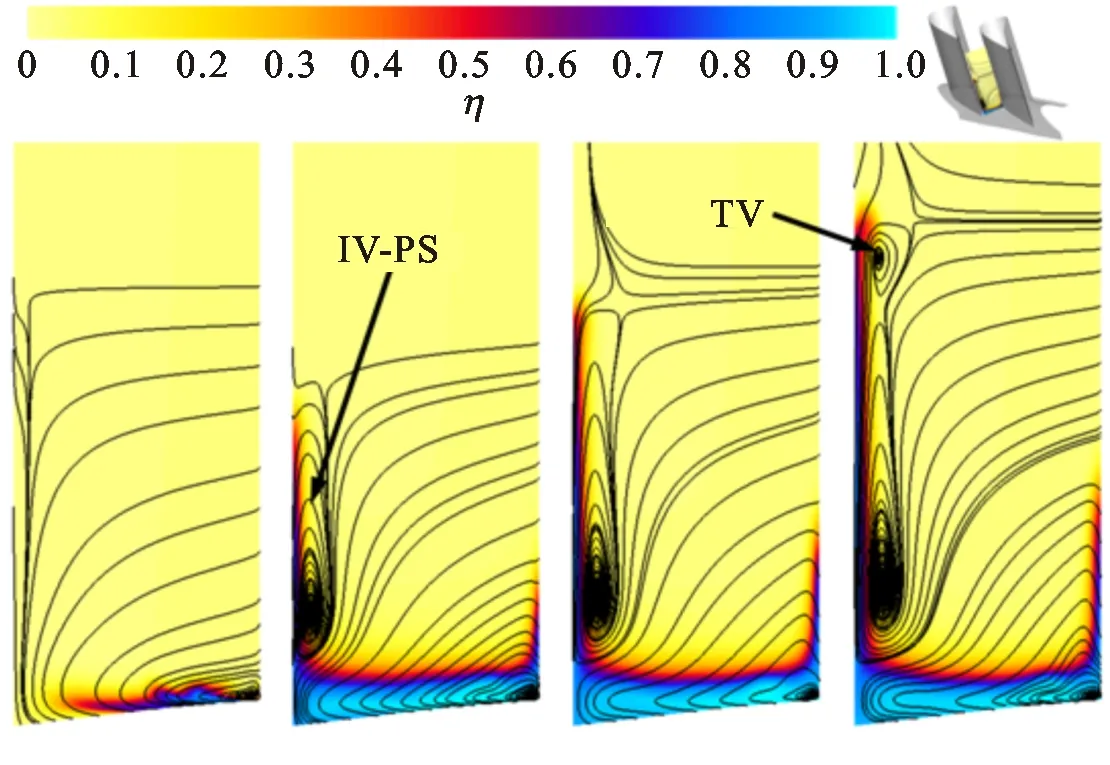
(a)工况1 (b)工况2 (c)工况3 (d)工况4图13 喉部截面温度场与平面流线图Fig.13 Temperature distributions and two-dimensional streamlines on the throat profile
如上所述,以冲击涡为代表的二次流结构会使由端壁位置流入的冷却气携带至叶表,形成泛冷却效果。图14给出了叶表绝热冷却有效度分布。在无发散冷却时,仅有吸力面尾缘部分存在泛冷却效果,是由SSGVs中位于下方的正涡量部分携带槽缝射流冷却气,在抵达吸力面后向上卷起形成的。存在发散冷却时,冲击涡会携带发散冷却气在压力面叶表上洗,形成明显的泛冷却效果。从上游至下游,冷却气在压力面叶表覆盖的展向距离不断增加,在吸力面侧其覆盖范围基本不变,且发散冷却气质量流量比越高,冷却气在吸力面与压力面的覆盖面积均增加,这是因为冲击涡得到了同步增强。

(a)工况1 (b)工况2

(c)工况3 (d)工况4虚线左侧为吸力面;虚线右侧为压力面。图14 叶表绝热冷却有效度分布Fig.14 Adiabatic cooling effectiveness distributions on vane surface
由于两种冷却结构注入位置与流量均差异较大,其流动分布情况也大不相同。本文以来自某结构冷却气对绝热冷却有效度的贡献程度代表冷却气在该区域的分布情况进行研究。Alqefl提出了多异温冷却气腔室综合冷却效果的标准化研究方法[3]
(5)
式中:n为冷却气腔室数;ηci为第i腔室单独供气时产生的冷却有效度;ηdi为第i个腔室冷却气无量纲温度,计算式为
(6)
其中Tci为第i个腔室冷却气温度,T∞为主流温度,Tc1一般选取为与主流温度差异最大的腔室冷却气温度。本文提出该方法的反问题,即根据多个冷却气腔室同时供气时的计算结果,分析来自单一腔室的冷却气对冷却效果的该贡献程度。参考式(5)多冷却气腔室综合冷却效果标准化研究方法,调整个别冷却气腔室供气温度,再将得到的绝热冷却有效度代入线性方程联立求解,即可得到单一腔室冷却气产生的冷却有效度贡献程度。以本文所研究的包含发散冷却与槽缝射流两个腔室的模型为例,在原始边界条件计算的基础上,改变发散冷却气温度进行计算,边界条件如表6所示。

表6 冷却气分布情况研究计算工况Table 6 Computational conditions for coolant distribution investigation
由式(5)可得
(7)
式中:ηA与ηB分别为工况A、B下的绝热冷却有效度;ηcE与ηcS分别为发散冷却与槽缝射流产生的绝热冷却有效度。在此基础上,可将发散冷却气对整体绝热冷却有效度的贡献占比定义为
fE=ηcE/ηA
(8)
相比于原多冷却气腔室标准化研究方法,本文所述研究方法的两种计算工况均由两个腔室同时供气且密度比差异不大,可以认为流动情况基本相同。采用该方法获取的来源于某结构的冷却气对绝热冷却有效度贡献程度,可以用来评估某冷却结构冷却气在特定位置的聚集情况,有助于理解不同冷却气的流动与发展。
图15给出了叶栅通道端壁与各截面发散冷却对绝热冷却有效度贡献占比分布,图中蓝色部分fE<50%,表明槽缝射流贡献了该区域的大部分冷却效果,而红色表明发散冷却主导该区域的冷却。另外,由于冷却气仅在壁面附近流动,图中各截面仅显示η>0.5的部位。整体趋势上,ME越高,fE越大。如图中x=-0.15Cax和x=0的截面,槽缝射流冷却气注入后在发散冷却气形成的气膜下方流动。压力面侧与吸力面侧上游fE较低。这是因为该位置静压较高,槽缝射流无法覆盖至该位置。除了吸力面叶片中下游位置有一些槽缝射流冷却气分布外,泛冷却效果几乎全部由发散冷却气贡献。这是因为发散冷却气在槽缝射流气膜上层流动,更容易在冲击涡与吸力面角涡的作用下发生沿叶片表面的上洗。在工况4中,可以观察到三次涡引起的压力面中间叶展位置冷却气聚集,如图15c所示。端壁中上游部分主要由槽缝射流冷却气进行冷却,而在边界层分离线下游,端壁几乎全部由发散冷却气覆盖,说明端壁横流对槽缝射流冷却气流动影响显著。
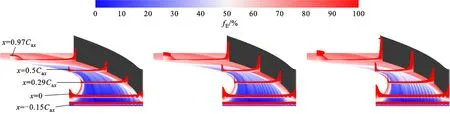
(a)工况2 (b)工况3 (c)工况4图15 叶栅通道端壁与各截面发散冷却对绝热冷却有效度贡献占比分布Fig.15 Contribution of effusion cooling to the adiabatic cooling effectiveness distribution on hub endwall and each profile
3 结 论
本文数值研究了燃烧室壁面发散冷却与槽缝射流冷却共同作用下,涡轮静叶造型端壁的二次流结构及冷却气流动情况,分析了不同发散冷却气质量流量比下端壁附近各种涡结构、总压损失系数和端壁、叶表绝热冷却有效度以及两种冷却气在端壁上的分布情况,得到如下结论。
(1)叶片吸力面侧存在由喉部位置开始形成的吸力面角区涡对;冷却气的注入使通道涡在叶栅通道内部始终在压力面侧发展,不会偏转至吸力面;部分槽缝射流在端壁造型开始位置形成回流涡,横向发展至低静压位置进入叶栅通道;发散冷却气质量流量比由5%增加至7%时,进口截面端壁附近的总压峰值升高3.7%,峰值区流体在叶片前缘滞止后向上卷起形成冲击涡;压力面侧分支得到发散冷却气冲击压力面充能,向中间叶展位置延伸,吸力面侧分支上方形成与其旋向相反的冲击涡诱导壁面涡。发散冷却流量增加时,冲击涡被增强而吸力面角区涡对被削弱。
(2)在无发散冷却与发散冷却流量较低时,出口截面仅存在一个总压损失峰值区,位于吸力面角区涡对交界处,发散冷却气质量流量比增加时,该位置总压损失减小;M>5%时,原总压损失区上方出现了新的高总压损失区,处于冲击涡吸力面侧分支与冲击涡诱导壁面涡之间,且该位置总压损失随M增加而增加;低流量冷却气会使整体总压损失降低,而M由5%升高至7%时总压损失增加4.5%。
(3)仅有槽缝射流时,叶片前缘、压力面角区等位置无法得到冷却气覆盖,且此时仅有吸力面叶片下游得到部分冷却;发散冷却气注入时,冲击涡会将冷却气携带至叶表,在压力面形成显著的泛冷却效果;较高的发散冷却流量(M=7%)会使冲击涡纵向伸长并分裂出三次涡。
(4)推导了发散冷却贡献占比的计算方法,边界层分离线上游端壁由槽缝射流冷却气覆盖,而叶表和下游端壁的冷却由发散冷却主导;在槽缝射流无法覆盖的压力面侧与吸力面侧上游位置,fE增长迅速。
(5)发散冷却气在流动过程中会发生明显温升,因此需要更深入地开展发散冷却对涡轮静叶传热与冷却特性影响特性的研究。同时,考虑开展发散冷却气影响的涡轮静叶冷却结构优化设计,以降低冷却气量、提高冷却效率和减小气动损失。

