建筑幕墙安装机器人的位置/力混合控制方法
胡河宇,曹建福,曹晔,陶必荣
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
在中国快速城市化进程中,出现了大量的高空建筑,幕墙已成为其主导性外部装饰[1]。作为具有巨大发展潜力的建筑施工自动化装备,幕墙安装机器人有着广泛的应用前景和研究价值。然而,由于不同工作场合和任务需求中存在着被安装幕墙的质量改变、幕墙与墙壁之间的接触介质和安装工艺不同、机器人动力学参数的漂移和偏差等问题[2],安装精度和安装效果被严重影响,这给幕墙安装机器人的位置/力混合控制带来了难题[3-4]。
幕墙安装时与环境发生接触前,对机器人而言是位置控制过程,目前的方法是在对幕墙运动过程进行分解的基础上再进行位置或者速度控制[5-6],如Sloth和Pedersen把玻璃幕墙安装任务分解为平动、滑动和提升共3种形式,根据参考速度和运动学模型设计了关节速度控制器[7]。当幕墙与墙壁接触时,需要对幕墙的安装位置及其与环境的接触力同时进行控制。为此:刘智光等研究了高空幕墙安装机器人的力控制问题,提出了基于动力学参数估计的自适应阻抗控制方法[8];陈贵亮等对幕墙安装机器人的柔顺操作策略进行研究,把幕墙的工作空间分为自由空间和接触空间,提出了基于自适应力的控制算法[9];李铁军等提出了基础阻抗控制和自适应阻抗控制相结合的控制策略,能够满足自由空间快速运动和接触空间力控制的准确性要求[10],更进一步提出了模型参考自适应控制方法[11]。这些工作对幕墙安装机器人的位置/力控制进行了研究,然而未进一步考虑幕墙质量和接触环境等发生变化对安装过程的影响。
未知不确定性是机器人控制的一个重要研究方向。对于动力学参数发生变化的传统机器人(非建筑机器人),文献[12-14]设计自适应律对不确定项进行补偿,文献[15-16]使用时间延迟估计对未知项进行逼近,文献[17]提出速度估计的策略,均可实现期望的位置控制目标。当机器人接触环境未知或者不确定时,文献[18-19]根据检测到的接触力来控制机器人在未知环境中做出相应的运动,文献[20]采用速度控制的方法解决位置/力控制问题,文献[21]采用神经网络对未知项进行估计,文献[22]采用变阻抗的控制方法。这些工作能够解决机器人动力学的不确定性和环境接触的不确定性问题,然而未考虑工作对象发生变化时的情况,也未研究多种未知项同时出现的情况。
针对建筑幕墙机器人的位置/力控制任务,本文通过分析幕墙重量、环境接触和机器人自身动力学参数等同时发生变化的情况,建立了含有不确定项的机器人-幕墙-接触环境综合动力学方程。结合自适应与阻抗控制方法,对安装机器人接触力进行柔顺控制,同时实现高精度的位置控制。
1 建筑幕墙安装机器人模型
建筑幕墙作业具有尺寸大、重量大和环境复杂等特点,使用通用工业机器人不能满足工程要求。图1为本文研究的幕墙安装机器人,其主要用于大型大理石、玻璃等外饰幕墙的吸取和安装,质量约为350 kg,工作半径为1.3 m,最大吸取质量为50 kg,末端安装有真空吸盘。本文通过对幕墙、接触环境和机器人分别建模,得到综合动力学模型。

图1 幕墙安装机器人Fig.1 Slabstone installing robot
1.1 幕墙的受力分析
建筑幕墙安装过程分为3个阶段:第1阶段,机器人从初始水平位置抓取幕墙之后,将其位姿调整至竖直状态,此过程中抓取力Fe向上且具有旋转分量,重力mag向下,如图2a所示,其中,ma表示幕墙质量,g表示重力加速度;第2阶段,幕墙在水平方向运动,直到与墙壁的位置临界接触,抓取力Fe在竖直方向上的分量抵消重力mag的影响,在水平方向的分量Fo使幕墙向墙壁方向运动,此过程中幕墙与墙壁的接触力Fin=0,如图2b所示;第3阶段,幕墙从临界接触状态运动至稳定接触状态,与第二阶段相比,幕墙与墙壁的接触力Fin≠0,如图2c所示。
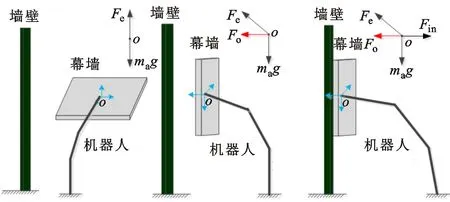
(a)第1阶段 (b)第2阶段 (c)第3阶段图2 幕墙安装过程示意Fig.2 Schematic diagram of slabstone installation process
幕墙的运动空间包含3个平移方向和3个旋转方向[23-24],其动力学参数主要受质量影响。在不同的任务中,幕墙的重量不同,且无法获得其准确值。本文建立动力学模型
(Ga(x)+ΔGa(x))=Fe-Fin
(1)
1.2 幕墙与环境的接触模型
幕墙与墙壁等环境之间的填充材料通常是水泥砂浆等柔性体。假设填充材料为均质分布,幕墙与环境之间的接触力位于法线方向,实验表明接触前期的形变位移和力之间基本为线性关系[25]。由于待安装幕墙及其工艺不同,与墙壁接触时的刚度系数不同且无法准确获得。当幕墙与外界环境接触如图2c所示时,可线性描述接触力模型
Fin=(Ke+ΔKe)Ee
(2)
Ee=x-xe
(3)
式中:Ke表示环境刚度系数的已知部分;ΔKe表示未知部分;xe表示安装环境所处位置;Ee表示环境接触误差。
1.3 幕墙安装机器人动力学模型
对于图1所示的六自由度幕墙安装机器人,假设连杆都是刚性的,末端的吸盘抓取幕墙后无相对位移,运动学模型精确已知,并且机器人在运行过程中躲避所有奇异位姿,自由度和空间维数均为6。由于存在的动力学参数漂移问题,在关节空间中机器人拉格朗日动力学方程表达式为
(4)

1.4 机器人与物体的综合动力学模型
根据式(1)~(4)可以得到机器人-幕墙-接触环境的综合动力学方程
(5)
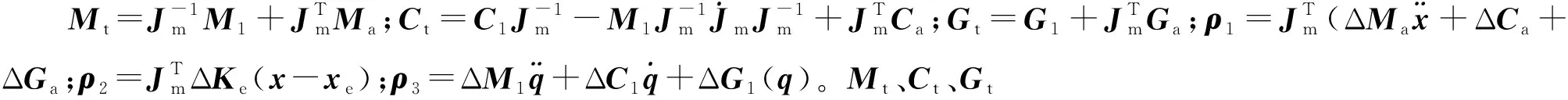
假设1幕墙质量变化范围有界,式(1)中的不确定项满足
(6)
式中a1、a2、a3为未知的非负实数。
假设2幕墙与墙壁之间的接触材料(如胶泥、混凝土等)改变时,环境接触刚度系数变化值有界,式(2)满足
‖ΔKe‖≤b
(7)
式中b未知的为非负实数。
假设3机器人本身参数的漂移和干扰项有界,式(4)中不确定项满足
(8)
式中c1、c2、c3为未知的非负实数。

2 控制器设计
幕墙安装机器人执行任务过程中,需要保证位置精度以及幕墙和墙壁接触之间的接触力平稳。因此,本文的控制目标为:①机器人沿着期望轨迹运动,即x→xd;②幕墙与墙壁之间的环境接触力Fin=Ke(x-xe),使得Fin→Fd。为达到该目标,本文提出了基于双环策略的阻抗自适应控制器,外环中使用阻抗控制模型处理环境接触力与位置的关系,在内环中设计自适应控制器补偿模型不确定项,实现幕墙的高精度位置控制轨迹。
2.1 阻抗控制模型
阻抗控制通过建立机器人末端作用力与位置之间的动态关系,达到控制环境接触力的目的,且运动过程平稳、抖动小。针对幕墙安装过程,在基础的阻抗控制算法中引入期望力Fd,建立阻抗关系
(9)
式中:E为需要补偿的阻抗偏差;Fd为期望力;Md、Bd、Kd表示阻抗模型中的质量、阻尼和刚度系数,通过调整此类阻抗参数值,可获得理想的力柔顺效果。根据式(9)中环境接触力与期望力的误差Fin-Fd,可计算出位置补偿值E,进而得到参考轨迹
xr=xd-E
(10)
式中xr为经阻抗模型补偿后的参考轨迹。本文设计自适应位置控制器,保证幕墙跟踪参考轨迹x→xr。
2.2 自适应控制器
机器人-幕墙-接触环境的综合动力学模型式(5)中存在着幕墙质量不确定、幕墙与环境的接触刚度不确定、机器人动力学参数漂移以及干扰项,给高精度位置控制带来了挑战。本文首先根据假设1~3提取出不确定项范数上界的粗糙信息,进而估计上界中参数不确定项,设计相应的自适应控制方法,保证幕墙跟踪参考轨迹xr,最后结合李雅普诺夫稳定性分析给出严格的证明。具体过程如下,首先定义误差项
e=x-xr
(11)
引入滤波误差S

(12)
式中常数λ>0。进而,设计控制器为
(13)
(14)
(15)
(16)
(17)

定理1考虑机器人与幕墙的综合动力学模型式(5),不确定项满足假设1~3,如果使用自适应控制器式(13)~(17),则可实现期望的跟踪目标且所有内部信号一致有界;对于任意有界的初始条件,所有内部信号均有界,控制信号均一致连续并且不需要考虑过多的初始条件。
证明由式(12)的Hurwitz特性可知,如果保证S→0,则e→0。定义关于滤波误差S的李雅普诺夫函数
(18)
对式(18)求导可得
(19)
根据系统模型式(5)可得
ρ1-ρ2-ρ3+τd
(20)
由式(12)(20)可得
(21)
将式(21)代入式(19)可得
τd)≤ST(-k0MtS+τ-ut)+‖S‖(‖ρ1‖+
‖ρ2‖+‖ρ3‖+‖τd‖)
(22)
根据假设1,幕墙动力学不确定项ρ1可表示为
(23)
式中a=max{a1,a2,a3}。
根据假设2,接触力的不确定项ρ2可表示为
(24)
根据假设3,机器人动力学参数的不确定性ρ3和干扰项τd可表示为
(25)
式中c=max{c1,c2,c3}。
将式(23)~(25)代入式(22)可得
aΦa‖S‖+bΦb‖S‖+cΦc‖S‖
(26)
根据杨氏不等式[27]可得
(27)
(28)
(29)
将式(27)~(29)代入式(26)可得
(30)
将式(13)代入式(30)可得
(31)
(32)
对式(32)求导可得
(33)
代入自适应律式(14)~(16)可得
(34)
再依据弹性不等式[27],得到
(35)
(36)
(37)
将式(35)~(37)代入式(34)可得
(38)
由此可得

(39)

(40)
在时间[0,t]上对式(40)进行积分,可以得到
(41)
由定理1的证明过程可知,系统模型存在不确定情况下,设计的控制器式(13)和自适应律式(14)~(16)可保证系统一致最终有界,实现期望的位置追踪目标。通过增大参数k0、k11、k21、k31,可减小滤波误差S,使误差e能够收敛到足够小的邻域内。
2.3 幕墙安装机器人的阻抗自适应控制器设计


图3 幕墙安装机器人位置/力控制框图Fig.3 Position/force control block diagram of slabstone installing robot
需要注意的是,文献[8-10]的幕墙安装机器人位置/力控制方案仅考虑机器人接触环境的改变。不同于这些结果,本文设计的阻抗自适应控制器可同时适应于幕墙质量变化、接触环境变化和机器人动力学参数漂移的情况。首先,利用模型的已知信息设计位置的控制器ut;其次,在线估计复杂环境(幕墙质量变化、接触环境变化和机器人动力学参数漂移)带来的参数不确定项,在内环控制中增加相应的自适应补偿项,提高位置的跟踪精度;最后,结合阻抗控制模型,实现位置和力的混合控制。除此之外,文献[8-10]设计的控制器需要使用机器人惯性矩阵的估计值,当机器人关节数增多时会导致计算的复杂性,本文设计的控制方法可以避免此类问题。
3 仿真验证
为研究所提出控制的特点及其效果,本文将六自由度建筑安装机器人串联结构模型简化为两关节的连杆结构,动力学与运动学公式与文献[10]相同。连杆质量及长度分别为:m1=200 kg,m2=900 kg;a1=1.080 m,a2=0.640 m。幕墙的动力学模型中,已知参数矩阵的表达式分别为
(42)
设定幕墙的初始位置为(0,1.2) m,期望位置为(1,1.2) m,环境接触位置为(0.999,1.2) m。阻抗系数为Md=[100,0;0,100],Bd=[1 000,0;0,1 000],Kd=[4 000,0;0,4 000]。幕墙与墙壁的环境接触刚度取值为Ke=[ke,0;0,0] N/m,ke=4 000,接触力方向矩阵W=[1,0;0,0]。期望力Fd=[3.3;0] N,重力加速度g=9.8 m/s2。控制器参数λ=100,k0=6,k11=0.001,k12=0.001,k13=0.000 4,k21=0.2,k22=0.000 3,k32=0.01。仿真时分别处理幕墙质量变化、接触环境改变以及机器人动力学参数漂移共3种情况,并与文献[10]中提出的方法进行结果对比。
3.1 幕墙质量变化
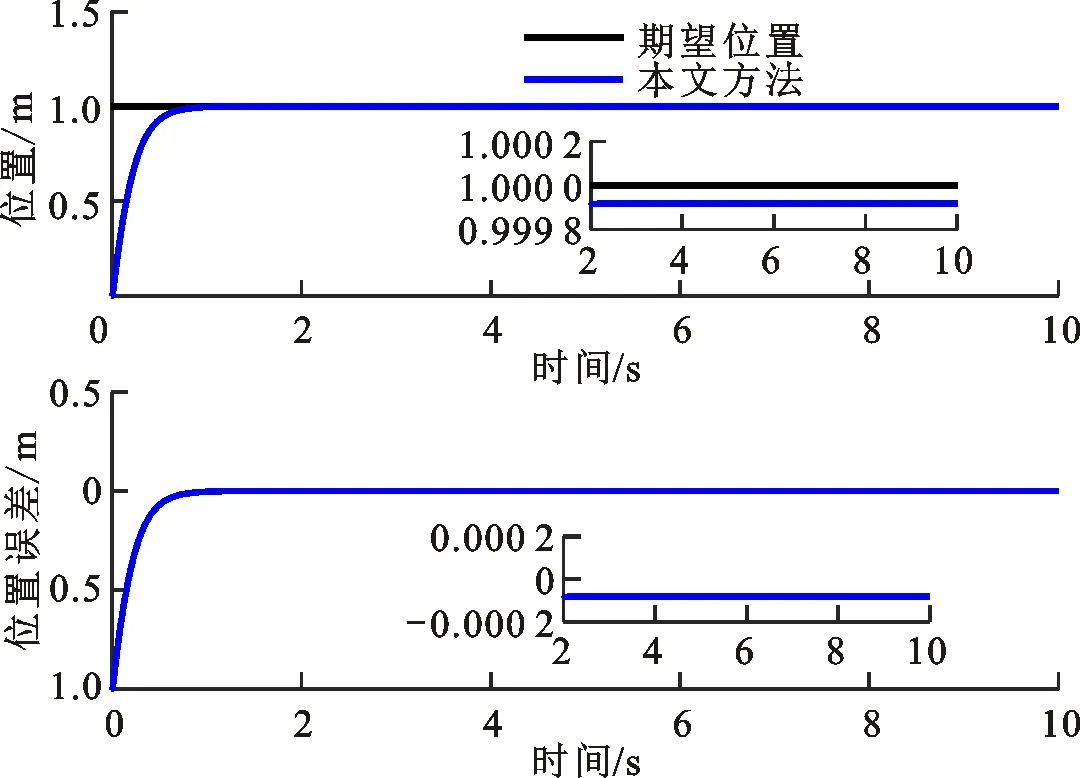
幕墙质量ma=300 kg时,文献[10]方法的位置/力跟踪结果如图4所示。可以看出,位置和接触力产生抖动会导致安装失败,原因是设计的控制器中未考虑幕墙质量,以致适用范围狭小。幕墙质量ma=200,600 kg,Δma=-100 kg时,本文方法的位置/力跟踪结果如图5和图6所示。可以看出,稳定接触的位置误差精度为0.20、0.08 mm,接触力误差分别为0.27、0.78 N。本小节结果表明,本文方法能够完成幕墙质量在0~600 kg之间的安装任务,适用的幕墙质量变化范围相比文献[10]方法更为宽广。
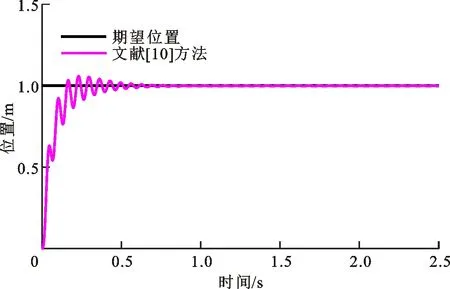
(a)位置跟踪结果

(b)接触力跟踪结果图4 ma=300 kg时文献[10]方法的位置/力跟踪结果Fig.4 Position/force tracking results of the method in ref.[10] when ma=300 kg
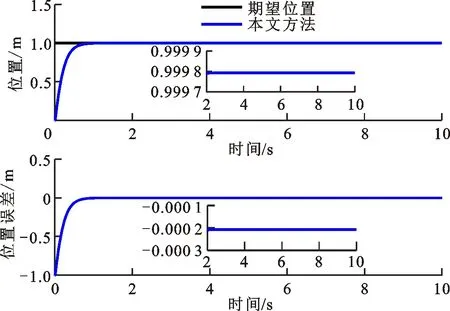
(a)位置跟踪结果

(b)接触力跟踪结果图5 ma=200 kg、Δma=-100 kg时本文方法的位置/力跟踪结果Fig.5 Position/force tracking results of the proposed method (ma=200 kg and Δma=-100 kg)
(a)位置跟踪结果

(b)接触力跟踪结果图6 ma=600 kg、Δma=-100 kg时本文方法的位置/力跟踪结果Fig.6 Position/force tracking results of the proposed method (ma=600 kg and Δma=-100 kg)
3.2 幕墙与墙壁之间接触环境变化
环境接触刚度ke=3 000,5 000 N/m时,本文方法和文献[10]方法的位置/力跟踪结果如图7和图8所示。可以看出,本文方法稳定接触的位置误差精度为0.13和0.17 mm,接触力误差为0.6和0.9 N。本文方法和文献[10]方法都能使机器人末端与环境的接触力最终维持在稳定的状态,实现对接触力和位置的控制。这是因为二者都考虑了接触环境变化的影响。由此可见,外界环境变化情况下,本文方法和文献[10]方法都能获得好的位置和力跟踪效果。

(a)位置跟踪结果
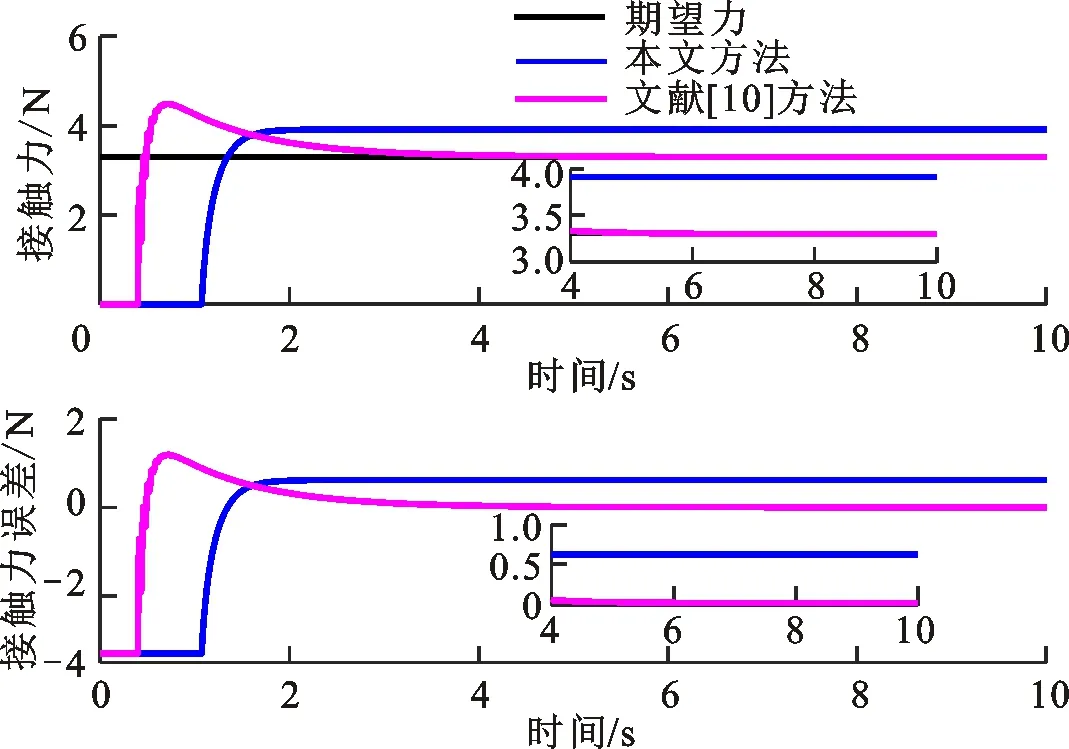
(b)力跟踪结果图7 ke=3 000 N/m时本文方法和文献[10]方法的位置/力跟踪结果Fig.7 Position/force tracking results of the methods in this paper and in ref.[10] (ke=3 000 N/m)
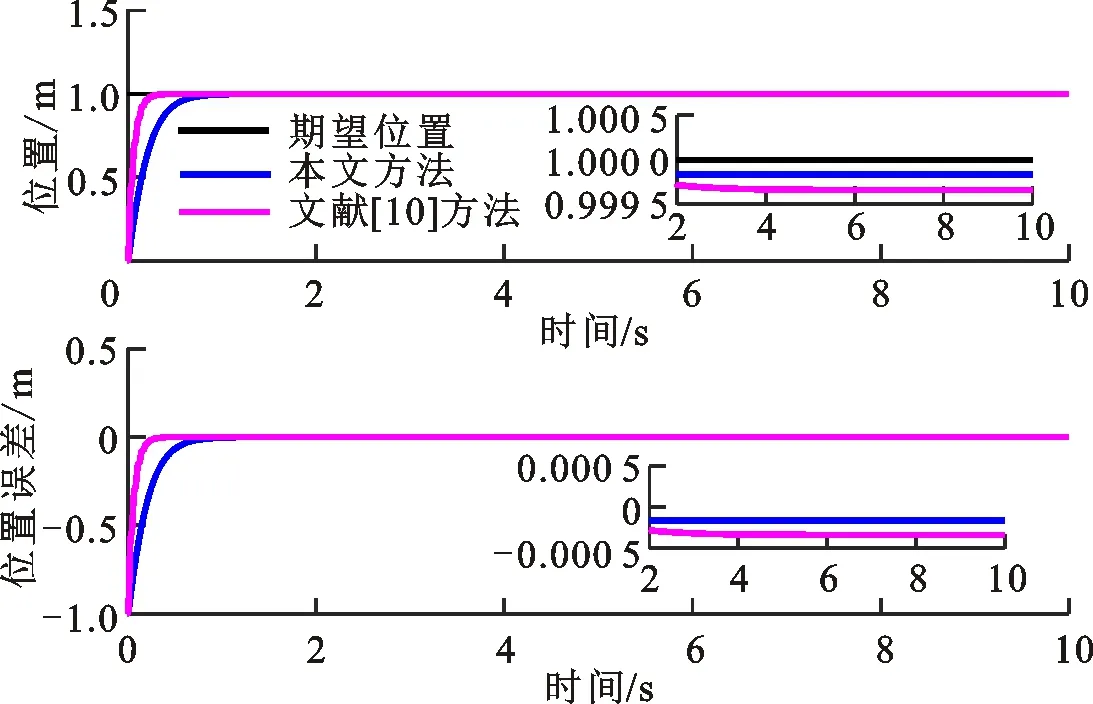
(a)位置跟踪结果

(b)接触力跟踪结果图8 ke=5 000 N/m时本文方法和文献[10]方法的位置/力跟踪结果Fig.8 Position/force tracking results of the methods in this paper and in ref.[10] (ke=5 000 N/m)
3.3 机器人参数漂移引起的动力学不确定
当动力学参数漂移量ΔM1=0.2M1时,采用文献[10]方法的位置/力跟踪结果如图9所示。可以看出,位置和接触力产生抖动导致安装失败,原因是文献[10]中使用机器人惯性矩阵的估计值代替真实值,不适用于此种工况。当动力学参数漂移量ΔM1分别为-0.2M1和0.2M1时,采用本文方法的位置/力跟踪结果如图10和图11所示。可以看出,稳定接触的位置误差精度为0.17和0.15 mm,接触力误差为0.36和0.42 N。本小节实验说明了本文方法的适用性更为广泛。

(a)位置跟踪结果

(b)接触力跟踪结果图9 ΔM1=0.2M1时文献[10]方法的位置/力跟踪结果Fig.9 Position/force tracking results of the method in ref.[10] as parameter shift term ΔM1=0.2M1

(a)位置跟踪结果

(b)接触力跟踪结果图10 ΔM1=-0.2M1时本文方法的位置/力跟踪结果Fig.10 Position/force tracking results of the proposed method as parameter shift term ΔM1=-0.2M1
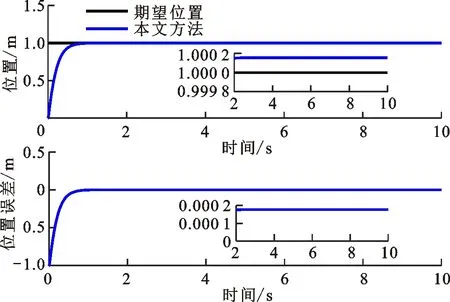
(a)位置跟踪结果
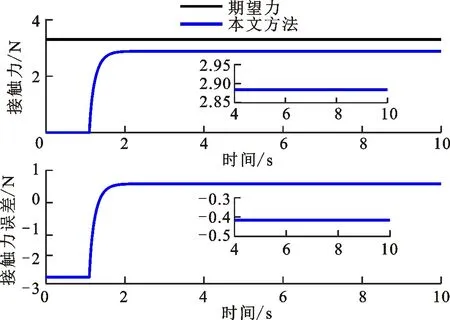
(b)接触力跟踪结果图11 ΔM1=0.2M1时本文方法的位置/力跟踪结果Fig.11 Position/force tracking results of the proposed method when parameter shift term ΔM1=0.2M1
4 结 论
本文研究了建筑作业场景下幕墙安装机器人工作过程中的位置/力混合控制方法,建模时考虑幕墙重量变化、接触环境改变和机器人动力学参数漂移,建立了包含3种不确定项的机器人-幕墙-接触环境综合动力学方程。为达到幕墙安装过程中位置/力的混合控制,在设计双环控制器时,外环中依据阻抗模型对位置/力进行平衡和实现柔顺控制,内环中设计不同的自适应律来处理3种不确定项,进而实现高精度的位置跟踪。该控制器充分利用了综合动力学方程中已知确定存在的参数,根据李雅普诺夫稳定性理论得出一致最终有界的结论。对不同任务需求中的幕墙安装过程进行仿真,结果表明,本文控制方法能够实现高精度的位置控制,接触力能够达到稳定状态。本文方法具有较强的可行性和合理性。

