断路器弹簧操动机构的等减速阶梯型缓冲器设计
万堃,奚延辉,王小鹏
(西安交通大学机械工程学院,710049,西安)
弹簧操动机构是高压断路器中最常见且使用最广的操动机构之一[1],它将驱动能量从分合闸弹簧传输到关节、连杆和链条上,利用弹簧压缩产生的能量驱动断路器的打开和关闭[2]。由于高压断路器的分合闸速度很高,弹簧操动机构需要安装缓冲器以吸收分闸时运动部分的动能,防止断路器中零部件因受到巨大的冲击而破坏[3]。若缓冲器设计不合理,造成过缓冲或者缓冲不充分的现象,都会影响到弹簧操动机构的分闸特性和使用寿命。因此,缓冲器设计的好坏直接关乎断路器性能的优劣[4-7]。
国内外学者对缓冲器做了大量研究。Farjoud等建立了单管液压缓冲器的非线性模型,研究了垫片组的特性及其对缓冲器整体性能的影响[8];Ferdek等探究了附加流道的应用对缓冲器特性的影响[9];郝鹏飞等对多孔型小型液压缓冲器的动态特性进行了深入的探讨与分析[10];刘波建立了各种缸内缓冲结构的缓冲过程的数学模型[11];Tvrdic等从动态强度计算的角度提出了一种再生式液压缓冲器的设计方案[12];张宏宇等以缓冲器的缓冲效率为优化目标,通过各类算法对液压缓冲器的结构参数进行了优化[13-17];钟山等提出在设计缓冲器时应考虑缓冲器外部特性对弹簧操动机构性能的影响,在Adams与MATLAB联合仿真的基础上,通过优化算法对弹簧操动机构缓冲器的结构参数进行了优化[18-19]。
现有研究主要针对缓冲器的缓冲特性分析及结构参数优化,没有系统地对弹簧操动机构用缓冲器的结构参数进行设计。此外,大部分文献将缓冲器的缓冲效率最大作为目标函数时,忽略了中间传动机构对缓冲器活塞及大质量部件运动关系的影响,而断路器弹簧操动机构中被缓冲对象复杂,设计的缓冲器难以最小化系统机械冲击。为此,本文基于弹簧操动机构的等效动力学模型,提出了以动触头等减速运动为设计目标的弹簧操动机构用缓冲器结构参数的设计方法,并利用虚拟样机技术进行验证。
1 等减速设计
1.1 弹簧操动机构分闸动作原理
某CT-Ⅳ型弹簧操动机构分闸原理如图1所示。图中,QA为拉杆,AB、BC、CD、DE为中间传动部件,OE为输出拐臂,OF、OH为主拐臂的不同部分。当弹簧操动机构接收到分闸信号,保持器的闭锁状态解除,分闸弹簧释放带动主拐臂及输出拐臂转动,并通过四杆机构将力传递给动触头完成分闸动作。主拐臂上的轴套F在缓冲器活塞杆的槽孔中运动,在运动到槽孔底部后撞击缓冲器活塞杆进行缓冲。

图1 弹簧操动机构分闸原理示意Fig.1 Schematic diagram of opening process of spring operating mechanism
1.2 等效动力学模型
为了简化分闸运动,以主拐臂OF为等效构件建立等效动力学模型,如图2所示。图中,Je为等效构件的等效转动惯量,Me为作用在等效构件上的等效力矩,ω为等效构件的角速度,即ωOF。
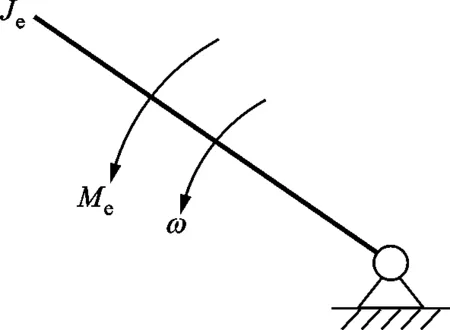
图2 等效构件示意Fig.2 Schematic diagram of the equivalent components
根据等效构件与机械系统的动能相等,求等效转动惯量
(1)
式中:Jsi为第i个构件对其质心轴的转动惯量;ωi为第i个构件的角速度;mi为第i个构件的质量;vsi为第i个构件质心处的速度。
当等效转动惯量及转动角加速度εOF已知时,其外力矩为
Me=JeεOF
(2)
根据等效构件与机械系统的瞬时功率相等,等效力矩还可以表示为
(3)
式中:Mi为第i个构件上的力矩;Fi为第i个构件上的力;αi为第i个构件质心处的速度vsi与作用力之间的夹角。
1.3 动触头等减速运动设计
要使高速运动的物体平稳地停止,理想的制动过程应以等减速的方式进行,而不应出现制动力峰值[20-23]。此前的研究往往将多个被缓冲对象视为整体,忽略了质量分布及运动关系的影响。弹簧操动机构系统中质量分布示意如图3所示。

图3 系统质量分布示意Fig.3 Schematic diagram of the mass distribution of the system
由于中间传动机构的存在,动触头与缓冲器活塞的运动关系呈高度非线性。显然,对于该系统而言,将多个被缓冲对象视为整体对缓冲器进行设计并不能使得系统最小化机械冲击。事实上,动触头及拉杆作为整个机械系统中质量最大的部分,其运动情况直接反映了断路器的分闸特性。依据分闸要求将动触头的运动设计成等减速的形式,可以在满足断路器分闸性能要求的基础上,最小化机械冲击。
根据断路器特性参数规定及相关经验,限定动触头在缓冲器刚作用时的速度vs及整个分闸结束的速度ve。缓冲器作用下的动触头位移是一定的,假定为S0。动触头的运动位移s(t)的规律可以表示为
(4)
某设计实例中动触头的位移时间曲线及速度时间曲线如图4所示。

(a)位移时间曲线 (b)速度时间曲线图4 动触头运动情况Fig.4 Movement of the moving contact
2 机构运动分析


图5 缓冲器作用时的机构运动简图Fig.5 Kinematic sketch under the action of shock absorber
分别对机构A-B-C、机构C-D-E-O、机构O-F-G、机构O-H-P进行分析。
(1)机构A-B-C。根据几何关系,有
(5)
据此,可以得到CB的角速度
(6)
(2)机构C-D-E-O。CD与CB的角速度相等,即ωCD=ωCB,故
(7)
另有几何关系
(8)
可以得到输出拐臂OE的角速度
(9)
另有ωOF=ωOE,可得主拐臂的角加速度
(10)
(3)机构O-F-G。角度φ6可以通过主拐臂角速度求得,即
(11)
根据几何关系
(12)
可得到缓冲器活塞杆的速度
(13)
(4)机构O-H-P。OF、OH为主拐臂不同部分,其角速度相同,则可以求得角度
(14)
有几何关系
(15)
可得分闸弹簧压缩改变量为
(16)
当动触头的运动规律确定时,根据本节分析可以求得缓冲器活塞、主拐臂的运动以及分闸弹簧的拉力。
3 阶梯型缓冲器设计
3.1 缓冲器缓冲原理
本文以侧切式阶梯型液压缓冲器为例阐述弹簧操动机构用缓冲器的设计方法。图6为该类缓冲器的结构示意,通过在活塞两侧铣平面的方式将活塞加工成阶梯状态,缓冲器的高压腔中充满液压油,低压腔中包含液压油和一定量的空气。密封装置能让低压腔中空气顺利排出而油液不被泄露。

图6 缓冲器结构示意Fig.6 Structure of the shock absorber
当活塞进入高压腔中,油液经过铣面与缸体形成的月牙形缝隙从高压腔压向低压腔,过流面积随行程不断变化,并形成缝隙节流缓冲。在整个缓冲过程中,主要是进入高压腔的铣面在起作用,为方便进一步表述缓冲器的缓冲动态特性,对进入高压腔的铣面进行编号,如图7所示。刚进入高压腔的铣面编号为n,代表缓冲进入到第n阶段;Li为活塞第i级铣面的长度;ci为第i级铣面的间距;S为活塞进入高压腔的行程。

图7 缓冲器活塞示意Fig.7 Schematic diagram of piston in shock absorber
每级节流缝隙的面积ai与铣面间距ci有关系式
(17)
式中:αi为节流缝隙对应的圆心角;r为高压腔(缓冲活塞)半径。
根据Bernoulli定理及阻力系数的计算公式,对缓冲压强进行计算。最终,可以将缓冲力表示为
Fh=f(ci,Li,d,ρ,μ,S,vh)
(18)
式中:d为高压腔直径;ρ为油液密度;μ为油液的动力黏度。
本文探讨缓冲器结构参数的设计,假定该缓冲器中采用的10号航空液压油的相关参数为常值。在20 ℃时,油液密度小于等于850 kg/m3,运动黏度小于等于23 mm2/s。
由于空间以及强度对缓冲器的限制,高压腔的直径d往往是固定的,而实际生产中对活塞进行加工是获得缓冲性能良好的缓冲器的最经济有效的方式,故对活塞铣面的间距及长度的设计进行介绍。
缓冲器的缓冲动态特性可近似表示为
(19)
缓冲力主要是由缓冲器活塞杆的速度、活塞进入高压腔的行程、各级铣面的间距和铣面长度决定。其中,每级铣面的长度决定了节流缝隙的分布情况及作用距离,铣面间距决定了节流缝隙的大小。
3.2 理想缓冲力曲线

(20)
根据式(20),可以计算出动触头等减速运动规律下缓冲器应当提供的理想缓冲力。但是,实际上在行程末期,随着速度的减小,节流缝隙即使很小也不能满足理想缓冲力的要求。缓冲器能提供的理想缓冲如图8所示,可以看出,缓冲器还需要借助缓冲垫吸收剩余的部分动能。

图8 理想缓冲力Fig.8 Ideal buffering force
虽然动触头以等减速运动的规律运动,并且分闸过程中的分闸弹簧拉力在不断减小,但计算得到的缓冲力却在增大。这是因为当动触头等减速运动时,主拐臂等并不是以线性减速的形式运动的。在运动末期,加速度的绝对值反而增大。分闸弹簧的拉力虽然在减小,但由于压缩量变化不大,拉力的变化并不大。
根据缓冲器的缓冲动态特性可知实际缓冲力的变化情况,每阶段实际缓冲力与理想缓冲力的变化趋势示意如图9所示。

图9 每阶段缓冲力的变化趋势Fig.9 Change trend of buffering force in each stage
显然,若不考虑每阶段缓冲力之间的过渡,则应让每段缓冲中间位移的缓冲力等于理想缓冲力,并使得中间位移两侧的缓冲力与理想缓冲力的差值接近且尽可能地小。这样才能使得每阶段缓冲力相对于理想缓冲力的增减量较小,保证实际缓冲力与理想缓冲力接近。
3.3 阶梯型缓冲器设计
铣面的长度及间距共同决定了节流缝隙对缓冲力的作用。当铣面长度确定时,依据理想缓冲力曲线及缓冲器的缓冲力表达式可以很容易地计算得到铣面间距。
结合缓冲器的缓冲动态特性,可以发现:
(1)缓冲力对速度的敏感性更大,速度较小时,节流缝隙面积需要做得很小以提供需要的缓冲力。但是,节流缝隙面积不能太小,否则夹渣时容易堵塞,导致缓冲失败。
(2)随着活塞行程的增大,活塞速度的变化率在不断增大,即相同的活塞位移下,前部分的速度减小更少。为使得每阶段的缓冲力理想缓冲力曲线接近,应尽可能地使行程靠前的铣面长度更长。铣面长度在设计时又不能太小,否则节流缝隙可能在使用寿命内因磨损等而失效。
对于缓冲器特性(1),在节流缝隙面积的限制下,为使得最后一段缓冲的最大缓冲力能接近理想缓冲力,需要预留一定的行程给最后一段铣面。即通过限定最大铣面间距,可以粗略计算得到最后一段铣面的长度。
对于缓冲器特性(2),根据分段长度的影响规律,引入等差数列来刻画前m-1段铣面长度递减取值最优的规律,即
(21)
式中m为铣面的总数。
显然,第m-1段铣面的长度是前m-1段铣面中最小的,有
Lm-1=L1+(m-2)ΔL
(22)
据此,提出一种阶梯型缓冲器的活塞铣面的设计方法:将缓冲器铣面长度设计问题转换为最大铣面间距及最小铣面长度的取值问题。限定最大铣面间距,设计最后一段铣面的长度;限定最小铣面长度,依据式(21)(22)所示的等差规律计算得到前m-1段的铣面长度;再取每级中间位移的缓冲力与理想缓冲力相等,求每级铣面的间距。
依此方法,本文提供的案例中每段缓冲力与理想缓冲力的拟合情况如图10所示,设计得到的缓冲器结构参数如表1所示。
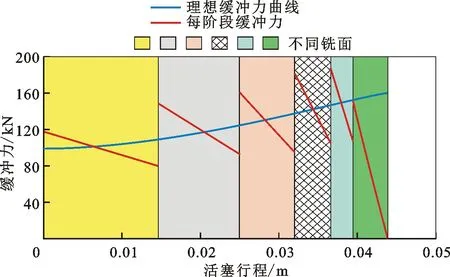
图10 每阶段缓冲力与理想缓冲力的拟合情况Fig.10 Fitting of buffering force of each stage with ideal buffering force

表1 本文案例的设计参数Table 1 Design parameters of the case
4 基于虚拟样机的验证分析
为了体现弹簧操动机构用缓冲器的缓冲作用,缩短开发周期,降低研发成本,本文通过ADAMS与MATLAB联合仿真的形式搭建起弹簧操动机构的虚拟样机模型,如图11所示。虚拟样机技术是一种通过在计算机上构建起虚拟样机模型,用数字化的形式代替传统物理样机的计算机辅助工程技术。虚拟样机在搭建成功的基础上,可以精确地分析、模拟和研究真实的系统的行为,是模拟和优化的有利工具[24]。
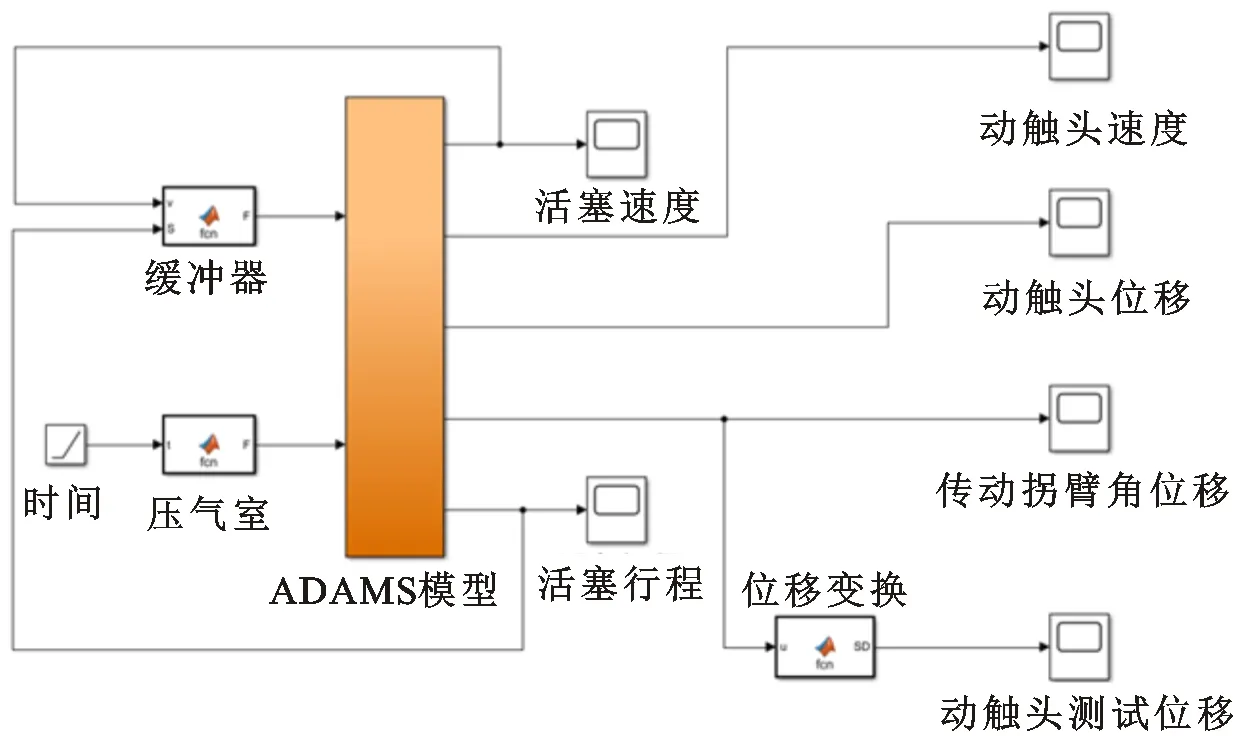
图11 弹簧操动机构虚拟样机Fig.11 Virtual prototype of spring operating mechanism
本文以同款CT-Ⅳ型弹簧操动机构的在运物理样机的缓冲器设计参数作为参照。虚拟样机与在运物理样机测量的分闸特性曲线如图12所示。

图12 分闸特性曲线对比Fig.12 Comparison of opening characteristic curves
可以看出,仿真曲线与实验曲线基本吻合。在后半段中,仿真曲线的斜率小于实验曲线的斜率,这是由于运动副间隙及杆件出现了一定变形,而ADAMS作为刚体动力学软件并不能反映这种情况。仿真与实验曲线误差在5%以内,这说明搭建的虚拟样机模型可靠正确。
虚拟样机加装和未加装设计缓冲器时的弹簧操动机构分闸特性曲线如图13所示。
由虚拟样机加装缓冲器和未加装缓冲器的分闸特性曲线可以看出,缓冲器在分闸过程中确实起到了重要作用。若不加装缓冲器,则会对系统的零部件产生巨大的冲击与破坏。本文方法设计出的缓冲器作用下的分闸特性曲线与经过反复修改调试的在运缓冲器分闸特性曲线较为接近,说明本文设计方法能较快地得到符合实际要求的缓冲器。并且,加装了设计的缓冲器的分闸特性曲线较在运缓冲器的缓冲时间增加了0.005 s,缓冲末速度减小了63%,分闸特性曲线更加平缓,未出现动触头在开断区间内停止的现象,说明缓冲器设计效果良好,设计方法可行。
5 结 论
(1)提出了一种以动触头等减速运动为设计目标的弹簧操动机构用缓冲器的设计方法。通过建立弹簧操动机构等效动力学模型的方式,计算使动触头等减速运动的理想缓冲力,结合缓冲器的缓冲动态特性,设计缓冲器的结构参数。
(2)探究了阶梯型缓冲器铣面长度及铣面间距等重要结构参数的设计方法,将缓冲器铣面长度及铣面间距的设计问题转换为最小铣面长度及最达铣面间距的取值问题。设计得到的分闸特性曲线平缓,末速度较在运缓冲器的更小,且未出现动触头在开断区间内停止的现象。
(3)本文缓冲器设计方法灵活可调。在设计过程中,根据缓冲效果,可以通过改变动触头的设计末速度调整缓冲过程,改善断路器的分闸特性。

