面向风力机叶片的平板超声微振动除冰

李岩，董笑宇，郭文峰，张影微

(1. 东北农业大学工程学院，黑龙江 哈尔滨150030； 2. 寒地农业可再生资源利用技术与装备黑龙江省重点实验室，黑龙江 哈尔滨150030)

风能是当前商业化运作最好的可再生能源之一，未来仍将保持持续稳定增长,有关风能高效利用的研究也层出不穷[1].然而，近年来全球气候变化加剧，极端气候频繁出现，对大型风力机产生了严重的影响[2-4].尤其是在寒冷潮湿地区，风力机叶片易发生结冰.导致了叶片翼型改变，破坏其气动性能，降低了风能利用率和发电效率；同时，结冰会导致叶片疲劳载荷变化，降低可靠性，影响安全稳定运行[5-6].国内外学者针对风力机叶片的结冰机理和气动特性影响进行了研究[7-8]，为开展防冰与除冰技术研发提供了依据.目前，风力机防除冰技术主要分为被动法和主动法[9].被动法主要是利用表面疏水涂层来进行防冰，但目前只能起到延缓结冰时间和结冰量的作用，完全实现防冰尚有很大难度.主动法主要有电加热法、热空气法、机械法和超声波法等，虽然各种方法都在一定程度上能够实现除冰，但也都存在各自的缺点，低能耗高效率的除冰方法仍在探索之中.

本研究关注的是超声波微振动除冰方法.该方法具有能耗低、结构简单和易于安装的特点.初期的超声波除冰技术研究主要针对覆冰的直升机桨叶[10-11]，近年来被用于风力机叶片除冰[12].

大型风力机叶片尺度大，虽然叶片翼型为曲线型，但在局部布置除冰元件时，可近似视为平板条件.因此，平板除冰是曲面除冰研究的重要基础.为此，文中拟利用仿真和试验相结合的手段，开展平板超声微振动除冰研究.首先利用ANSYS有限元软件模态分析铝板结冰体模型的振型及其固有频率随冰层厚度的变化规律.谐响应分析在不同冰层厚度、铝板基体尺寸和激励电压条件下，冰层与铝板基体黏着面的剪应力大小及其分布规律随激励频率的变化规律，以获得较好的除冰剪应力分布规律和冰层厚度.搭建超声振动除冰试验系统，验证其除冰效果，测量冰层黏着力随频率的变化规律.

1 仿真分析

由于铝制材料导热性稳定，选取小尺寸矩形铝板作为超声波除冰对象开展理论和试验研究，探索超声微振动除冰的基本规律，后续再开展针对各种实际风力机叶片复合材料的深入研究.

1.1 除冰原理

图1为超声波振动除冰原理图.压电陶瓷粘贴于铝板结冰体背面，即铝板非结冰面.当压电陶瓷在高频电压激励下，产生伸缩变形，从而激励铝板结冰体高频振动，产生弹性形变.当铝板结冰体弯曲变形时，在冰层黏着面或分界面将产生剪应力τ.现有研究结果表明，冰层与金属基体间的切向黏着剪应力较小，通过施加切向剪应力较易去除结冰体表面的冰层.当黏着面剪应力大于冰层切向黏着剪应力时，冰层与基体分离.因此，通过超声激振使铝板结冰体产生弯曲变形，从而在冰层黏着面产生切向剪应力，去除冰层或减小冰层黏着力.

图1 超声微振动除冰原理

1.2 模态分析

利用ANSYS仿真计算铝板结冰体振型固有频率随冰层厚度的变化规律，结冰体模型如图2所示.

图2 结冰体模型示意图

由图2可见，该结冰模型由冰层和铝板2个部分组成，其材料参数如表1所示，表中ρ为密度，E为弹性模量，μ为泊松比.

表1 材料参数

选取铝板边长为80 mm× 80 mm，厚度为0.5～3.0 mm，冰层厚度为0～15 mm的铝板结冰体开展模态分析，约束条件为四边固定.以铝板厚度为2 mm，冰层厚度为1 mm的仿真结果为例，前4阶振型云图如图3所示，图中UZ为沿Z轴方向相对位移.

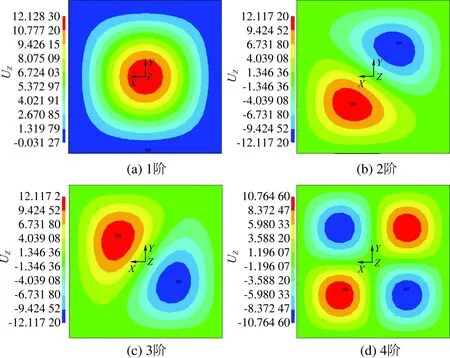
图3 结冰体振型云图

由图3可见，4种振型中，1阶振型的弯曲变形范围最大，更易激发出铝板的弯曲变形.因此，选取1阶振型为研究对象，铝板结冰体中心位置为激振源.不同铝板厚度和冰层厚度条件下的1阶固有频率的仿真计算结果如图4所示，图中k为固有频率，h为冰层厚度.

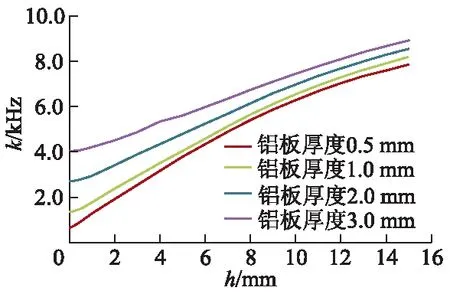
图4 结冰体1阶固有频率随冰层厚度的变化

由图4可见，当铝板基体尺寸不变时，不同铝板厚度的结冰体1阶固有频率随冰层厚度的增加而增加，其增长率呈先增后减的变化规律，铝板结冰体冰层厚度越小，其固有频率越低.该结果表明，振型相同时，冰层厚度薄，超声振动除冰系统的除冰频率越低.

此外，从图4中还可以看出，当铝板基体厚度较薄时，结冰体的固有频率增速较快；当铝板基体厚度较厚时，结冰体的固有频率增速较缓.因此，在铝板厚度较厚的条件下，冰层厚度的改变对除冰系统的除冰频率影响较小，系统工作稳定.

1.3 黏着面剪应力分析

在超声振动激励的作用下，在冰层黏着面产生剪应力，该剪应力的大小对冰层黏着力产生重要影响.根据仿真结果，选取压电陶瓷的尺寸为20 mm×20 mm×2 mm.铝板尺寸为80 mm×80 mm×2 mm，压电陶瓷类型为PZT-4，其性能参数如表2所示，其中s为柔度矩阵常数，e为压电常数，ε为介电常数.

表2 PZT-4材料参数

铝板厚度为2 mm，激励电压峰峰值Vp-p=400 V，冰层厚度为0.5～4.0 mm，谐响应分析在不同冰层厚度条件下冰层黏着面剪应力τ的分布及其随激励频率f的变化规律，激励频率步长为0.5 kHz，谐响应分析结果如图5所示，其中τmax为最大剪应力. 现有研究结果表明，冰层与金属基体的黏着剪应力最大值所在范围为0.24～1.70 MPa[13].选取各冰层厚度条件下最大剪应力为分析对象.当冰层厚度为0.5 mm，激励频率为31.0 kHz时，剪应力最大，为92.90 MPa.同理，当冰层厚度为1.0,2.0,3.0,4.0 mm时，激励频率分别为18.0, 49.0, 83.0, 90.5 kHz时，剪应力最大，分别为6.7,5.1, 8.2, 5.0 MPa，如表3所示,P为除冰面积比.

表3 4种激励频率下的除冰面积比

图5 冰层黏着面最大剪应力随激励频率的变化

图6为各频率点剪应力分布云图.由图6a可见，当冰层厚度为0.5 mm时，平板中心区域的剪应力大，该剪应力分布规律适于去除位于中心区域的块状覆冰层.由图6b可见，当冰层厚度为1.0 mm时，正负剪应力分布均匀且呈块状交错分布，该分布规律适于去除较大面积的片状覆冰.

由图6c可见，当冰厚为2.0 mm时，剪应力分布规律与冰厚1.0 mm的相似，但块状区域面积减小，数量增多.由图6d可见，当冰厚为3.0 mm时，黏着面中心区域的剪应力较小，但外围区域呈形状不规则的正负剪应力交错分布状态，适于去除边缘区域内的块状覆冰.由图6e可见，当冰厚为4.0 mm时，黏着面四角区域剪应力较大，适于去除块状覆冰.

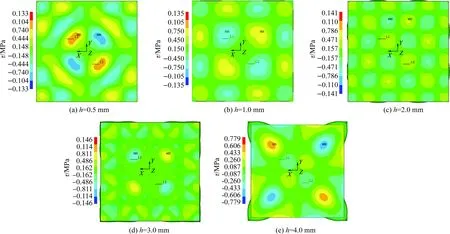
图6 冰层与铝板基体分界面剪应力分布云图

理论上，当黏着面剪应力超过冰层黏着剪应力时，冰层从铝板基体上脱落.因此，研究冰层黏着面剪应力大小及其分布具有重要的意义.以往虽研究了冰层黏着面最大剪应力随激励频率的变化规律，但能达到除冰作用的剪应力所占据的比例未量化分析.为量化分析超声振动对冰层黏着力和除冰效果的影响，文中提出“除冰面积比”的概念，量化在冰层黏着面中大于冰层黏着力的剪应力所占据的比例，计算公式为

(1)

式中：S1为冰层黏着面剪应力大于冰层黏着剪应力区域面积；S为基体覆冰面积.

根据式(1)分别对上述4种除冰工况的除冰面积比进行计算，计算结果如表3所示.由表可知，当冰层厚为0.5 mm时，黏着面最大剪应力为9.29×107Pa，除冰面积比为92.80%，除冰效果最好；当冰层厚度为1.0，2.0，3.0，4.0 mm时，除冰面积比分别为52.08%，47.32%，29.76%和32.56%，除冰效果显著降低.此外，当冰层厚度为1.0 mm和2.0 mm时，其除冰面积比远大于冰层厚度为3.0 mm和4.0 mm的除冰面积比.前两者最大剪应力较小但除冰面积比更大.

1.4 激励电压影响

当激励电压Vp-p为400 ～1 000 V时，上述4种工况冰层黏着面最大剪应力和除冰面积比的变化如图7所示.在各工况下，冰层黏着面最大剪应力均随激励电压的增加呈线性增长，但除冰面积比呈非线性增长，且增长率逐渐减小.

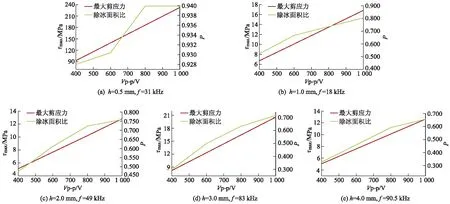
图7 最大剪应力和除冰面积比随激励电压的变化

由图7a可见，当冰层厚度为0.5 mm时，除冰面积比在初始阶段随激励电压增加呈增长趋势，当激励电压达到800 V时，除冰面积比达到最大值93.99%，但除冰面积比仅增加1.19%；由图7b可见，当冰层厚度为1.0 mm，激励频率为18 kHz时，除冰面积比增加27.62%.由图7c可见，当冰层厚度为2.0 mm时，除冰面积比增加28.1%；由图7d可见，当冰层厚度为3.0 mm时，除冰面积比增加41.85%；由图7e可见，当冰层厚度为4.0 mm时，除冰面积比增加33.09%.上述结果表明，增加激励电压可以提高除冰能力和效率.

2 试 验

结合理论计算结果和实验室现有的试验条件以及冰层样件的制作能力，选取冰层厚度为2 mm的铝板结冰体开展试验研究.测量冰层切向黏着剪应力随超声激励频率的变化规律，分析超声振动对冰层黏着力的影响及其除冰效果.

2.1 试验方案

试验选取的铝板尺寸为80 mm×80 mm×2 mm，压电陶瓷尺寸为20 mm×20 mm×2 mm，试验温度为-18 ℃，激励电压为正弦电压，其峰峰值Vp-p为400 V.根据理论计算结果，试验选取激励频率分别为47，49，51，83，85，87 kHz和无激励6种工况开展试验研究.

2.2 试验系统

该系统由信号发生器、超声功率放大器和冰层黏着力测量装置组成，系统示意图如图8所示.

由图8可见，冰层黏着力测量装置用于测量铝板结冰体冰层的扭转黏着扭矩，其结构如图9所示.

图8 试验系统

由图9可见，铝板结冰体被固定在测量装置的框架上，该框架为中空结构，为铝板背面的压电陶瓷提供空间，并固定在底座上.制作铝板结冰体样件时，预先将旋转头与冰层冻结为一体.在法兰端，利用机械式扭力计对旋转头缓慢地施加扭矩，使冰层与基体分离，并测得冰层的黏着扭矩.根据扭矩测量结果和建立的数学模型，计算出冰层与基体间的黏着剪应力.

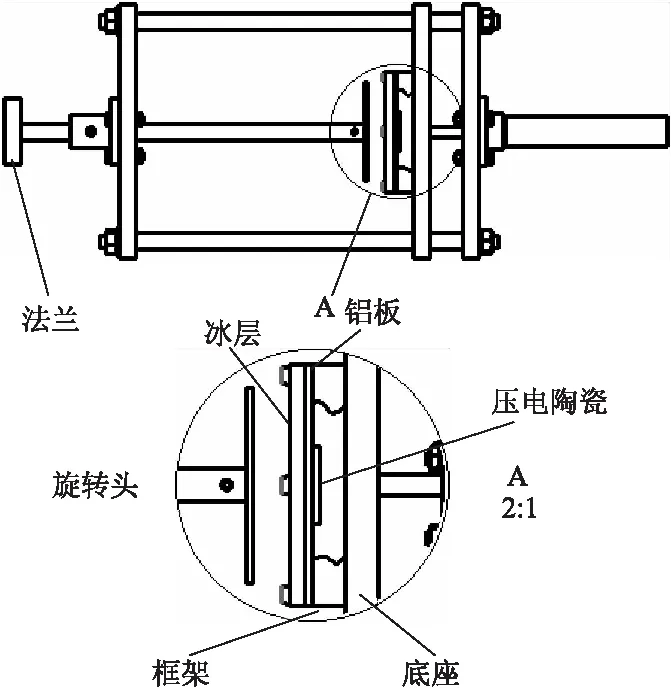
图9 冰层扭转黏着力测量装置

2.3 试验结果与分析

根据图2所示的结冰体模型，建立了计算冰层扭转黏着剪应力的数学模型，建模原理如图10所示.

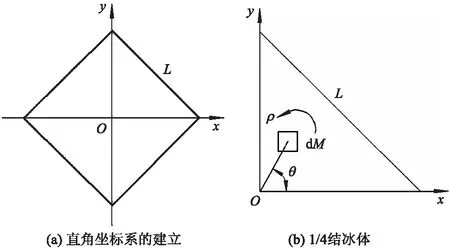
图10 冰层扭转黏着剪应力建模原理

由图10a可见，直角坐标系轴线与结冰体对角线重合，选取结冰体的1/4进行建模，如图10b所示.

由于积分区间的轴对称性，利用极坐标形式简化被积函数的积分形式，建立极坐标系下冰层微元的黏着扭矩计算公式，即

dM=τaρ2dρdθ，

(2)

式中：dM为冰层微元黏着扭矩；τa为冰层扭转黏着剪应力；ρ为冰层微元极径；θ为冰层微元极角.

根据图10b中极角和极径的变化范围以及式(2)，铝板结冰体黏着扭矩M为

(3)

式中：L为结冰体边长.

将式(3)积分，得冰层扭转黏着剪应力的计算公式为

(4)

为提高试验数据的准确度和可信度，每种试验条件下的冰层扭转黏着扭矩被测量5次，并将扭矩测量值M代入式(4)，计算得出不同激励频率下冰层扭转黏着剪应力τa.在此基础上，计算各工况下剪应力Ia的平均值及其标准偏差，计算结果如图11所示.

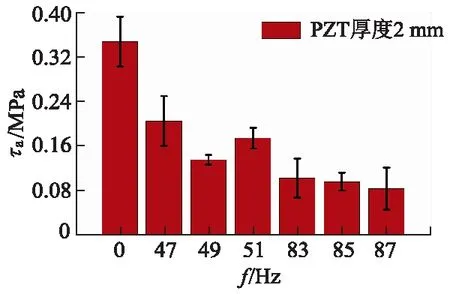
图11 冰层扭转黏着剪应力随频率的变化

由图11可见，当无超声振动时，冰层扭转黏着剪应力τa约为0.35 MPa.当激振频率f为87 kHz时，冰层扭转黏着剪应力最小，约为0.08 MPa，为无超声振动条件下冰层扭转黏着剪应力的23.7%；当激励频率在83～87 kHz时，冰层扭转黏着剪应力整体上小于47～51 kHz内的冰层扭转黏着剪应力.该试验结果表明，冰层黏着面在87 kHz的激振条件下弯曲变形较大，黏着面剪应力较高，冰层黏着力显著减小.

该试验结果与理论计算结果存在差异，分析导致该差异性的主要来源于结冰体样件制作尺寸的误差、铝板结冰体约束条件的差异性、材料参数的误差、结冰体结冰条件的误差和电源激励条件的误差.上述试验结果表明，超声振动虽未能去除铝板表面的冰层，但可以显著减小冰层黏着力，降低除冰难度.

3 结 论

利用有限元仿真和试验研究了超声振动对铝板表面冰层黏着力的影响，获得以下结论：

1) 当振型不变时，铝板结冰体固有频率随冰层厚度的增加而增长，其增长率呈先增后减的变化规律.冰层厚度越薄，超声振动除冰系统的除冰频率越低，除冰能耗越少.

2) 当冰层厚度为0.5 mm时，冰层黏着面剪应力和除冰面积比最大，冰层黏着面最大剪应力随激励电压的增加呈线性增长，除冰面积比呈非线性增长，且增长率逐渐减小.

3) 在超声波振动的作用下，冰层黏着力显著降低.当激励频率为87 kHz时，冰层扭转黏着剪应力最低，为0.083 MPa，黏着剪应力减小76.3%.