小波技术在“数字图像处理”课程中的教学应用

张湃，王丽侠

（唐山学院智能工程学院，河北唐山，063000）

0 引言

为切实响应教育部《关于深化本科教育教学改革全面提高人才培养质量的意见》的的内容，支持学生尽早进入项目、实验室和团队，通过先进的研究提高学生的创新能力和实践能力。近年来，本教研组致力于实施数学，在图像去噪领域学习优秀，从研究内容和成果到数学建模课程教学，逐步形成了以质量、应用、研究为目标的多层次、创新的人才学习方式，取得了良好的实践教学效果。

目前，图像已经进入人类社会生活的各个领域。通常情况下，采集的图像包含噪声[1]。噪声被定义为“阻止人体器官理解其接收到的源信息的因素”。特别是数字图像；由于信噪比可以准确地描述噪声对图像质量和图像质量的影响，因此噪声水平是通过信噪比（SNR）来测量的。

在现有的算法中，代表小波变换域的最先进的全局软阈值图像[2]，但它存在缺陷，容易产生“扼杀”现象。本设计提出了一种新的图像尺度模型，这意味着实验。通过分析波衰减后图像尺度之间的关系，定义了去除图像噪声的局部自适应阈值，并利用数字图像等课程知识，使学生能够利用波浪尺度信息设计自适应局部阈值。通过本设计的实践和实施，扩展和巩固学生所学的基础理论和专业知识，培养学生学习和使用新知识的能力。

1 图像尺度模型去噪原理

小波变换[3-5]是一种时频分析，它可以同时在频域和频域内分析信号，从而有效区分信号和噪声的尖锐部分，了解信号降噪过程。它具有高频率分辨率和低时间分辨率低频。它在高频段具有高时间分辨率和低频率分辨率。它非常适合检测和显示正常信号中的瞬态异常现象。它在处理非平稳信号时显示出强大的优势；以及图像信号去噪。

一般来说，有用信号通常是低频信号或一些相对稳定的信号，而噪声信号通常是高频信号。因此，降低噪声水平的过程主要包括以下处理：初始信号被波光衰减，噪声级通常被高频系数覆盖；然后以阈值的形式确定波衰减的高频系数。

基本波去噪就是找到从实际信号空间到房间波长函数的最佳映射，以获得原始信号的最佳恢复。波去噪实际上是边界挖掘和低容量过滤功能的综合。

基于小波变换寻找去除噪声的最佳方法的过程实际上就是寻找处理波系数的最佳方法的过程。常用的去噪方法可分为三类：①模极大值检测法；②小波系数相关去噪法；③阈值去噪法。

■1.1 模极大值检测法

信号奇异性表示某个信号在某处被中断，或一系列导数被中断或中断。显然，无限推断函数是平滑的或不是奇异的。唯一的一点，这是信号的突变，Lipschitz指数与小波变换后的局部最大系数模量相关。在不同尺度上波动后，在局部最大阻尼率下测量信号的局部奇异性。模极大值效用信号和噪声波变换在多尺度分析中表现出不同的奇异性，以消除噪声产生的模极大值点，保留模极大值产生的信号。最后，利用剩余模极大值估计波系数，然后使用估计的小波系数来恢复信号。该算法的基本过程是：

(1)原始信号已从波分解，并计算每个尺度的模极大值小波变换系数；

(2)阈值处理从最高刻度开始，如果模块最大点振幅的绝对值超过指定阈值，则必须保留一个点，否则必须删除一个点；

(3)根据模极大值估计和计算Wavel系数，以维持每个尺度；

(4)根据估计的波长系数恢复信号。

如果使用模的最大检测方法进行脱模，脱模效果对噪声的依赖性较小，性能稳定。如果图像中含有白噪声和更多的奇异点，则表示的图像不会有过度的振动，可以达到较高的信噪比。在使用这种方法时，还应注意波系数的尺度、阈值和计算方法的评估。

■1.2 小波系数相关法

小波域滤波应根据不同尺度上不同形式的信号和噪声设计相应的去除规则，以便对波信号和噪声系数进行处理。与噪声相对应，同时，与有效信号相对应的波速系数得到了最大程度的保持。但是与相应噪声相对应的波长系数不是那么明显的相关尺度。通过转换图像的多层波形因子，可以计算相邻尺度之间波形转换系数的相关性，利用不同尺度上波长系数的相关性可以区分信号系数和噪声系数，可以在信号和噪声之间进行选择，最后选择后的信号可以恢复到估计的波长系数。

在该方法中，保留所有低分辨率（大尺度）的小波变换系数，高分辨率（小尺度）的小波变换系数仅当它们是边缘附近的固定点时才保留，由于波浪噪声转换主要集中在小尺度水平，经过上述处理后，噪声基本消除，伺服信息得到更好的维护。算法的基本过程是：

(1)波在初始信号处分解；

(2)计算波衰减后的信号波速系数，并将相关系数归一化；

(3)如果给定标度上某一点的归一化系数大于同一标度点的波浪系数，则认为该点的波浪层系数由信号产生，且适当的措施会增加该点的相应振幅系数。该点处的波浪系数值由该点处的归一化系数确定，该点处的波浪系数视为确定。否则，该点处的波浪系数被认为是由噪声引起的，该点处的波浪系数已存活，归一化波浪系数确定为0。然后，应在每个标度上重新计算归一化系数；

用去噪法计算小波的相关系数的想法很简单，但计算量大，必须重复多次，并且给定点的相关系数仅由两个相邻尺度的波长系数确定。如果波衰减有误差，相关系数可能不会真正反映在相关点上，因此，如何有效、正确地计算相关系数以及如何选择阈值仍然是一个需要讨论的问题。

■1.3 去噪方法阈值

阈值去噪方法是通过小波变换图像得到小波变换系数，由于信号波系数包含重要信息，其数据较小，振幅变化较大，然而，波信号系数与噪声正好相反。通过建立一个特定的阈值，可以对小波系数进行交易，从而获得小波系数的估计值。最后，可以获得一个表示图像，该算法基于以下过程：

(1)波在初始信号处分解；

(2)确定波点的系数以获得估计的波系数；

(3)应根据估计的波长系数进行波长重建。

阈值去噪方法应用简单，计算量小，在实际中应用广泛。有两种阈值处理方法：一种是重阈值法，硬阈值法得到的波的连续性差，恢复的信号可能是突变或振荡，第二种是软阈值法，软阈值法得到的波系数一致性好，但如果小波系数较高，则处理后的波系数与实际波系数之间存在一定的差异，从而导致重建结果存在误差。

如果选择的阈值太高或太低，则在保留图像细节和边缘信息的同时无法取消该阈值。目前，阈值的选择和使用可分为全局阈值和局部自适应阈值。根据不同地层方向选择局部阈值。

设一个含噪声的信号的模型可以表示成如下形式：

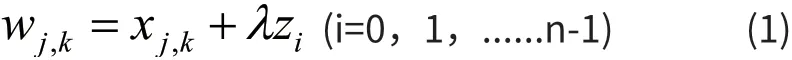
其中，zi代表高斯白噪声，λ是噪声级，n是信号长度。若要从被噪声污染的信号wj,k中恢复出原始信号ix，则基于小波分析的去噪方法分为以下3个步骤：

(1)计算含噪信号的交叉波转换，选择合适的波和波衰减层对含噪信号进行分解，得到相应的波衰减系数，包括低频系数和高频系数。

(2)已在阈值范围内处理退化的波浪系数。已选择适当的阈值处理各层的波速系数。

(3)对逆波进行变换。恢复阈值处理后的波系数，以获得恢复后的初始信号估计。

在小波变换域去噪中，通常根据小波变换退化后各层的分布系数选择不同的阈值。这种自适应阈值代表了一种算法，它很好地保留了图像的细节，因此得到了广泛的应用。在讨论之前，如何确定小波变换去噪算法，对小波变换系数进行了分析。

小波变换分解的系数近似等于高斯分布（GD）或近似拉普拉斯分布[6]，阈值表达式如下：

式中，nσ为噪声的标准差，α是信号的标准差，即所以式(2)可以重写为:

对于nσ可以通过下式来计算:

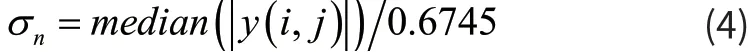
2 图像尺度模型去噪设计

该项目生成的成像比例模型的退出测试允许理解指示空域算法的自适应软阈值。该方法评估信号的能量，计算总矩阵方差，并将单个系数的处理考虑在内。比例模型已应用于比例室各个层面各个方向的小波变换域。该部分系数的方差应计算为与矩阵和噪声相关的该部分系数的能量。定义小波变换系数的尺度值为Z(i,j)：

S是小波变换分解后朝向下曲率的邻域系数，通常取3×3，N是系数S的系数。实际上，可以根据需要调整邻域中的图像内容。

(1)对噪声图像进行小波变换分解；

(2)用尺度模型将小波变换域内各级尺度空间的各个方向的小波变换系数矩阵分成多个部分。尺度值越小，分得越细。计算每部分的方差，并按式(3)计算噪声方差；

(3)根据公式（4）获得每个分量的信号容差和相应的阈值；

(4)软阈值用于表示波层到矩阵的转换系数，并用于波层转换系数的不同分类；

(5)去噪后重构小波变换系数。

在小波域去噪中，通常根据小波退化后各层的分布系数选择不同的阈值。这种自适应阈值代表了一种算法，它很好地保留了图像的细节，因此得到了广泛的应用。在讨论之前，如何确定小波变换去噪算法，对小波变换系数进行了分析。

图1 表示波层改变Lena分解图像后，最佳层和粗糙层在一个方向上的次曲率系数。该图是y系数的值，N是系数的数目。这可以被视为图像分解波变换的系数变化很小的指标，能量集中在有限系数t上在转置域中，大多数其他系数几乎为零。

图1 三组硬阈值、软阈值、本设计去噪效果仿真图

命名也受阈值选择的影响，其值不相同。确定限值和标准差表示谴责效应和阈值之间的选择关系。在标准差的情况下，不同的值对谴责有不同的影响。现在比较三组去噪效果：

与上述三类图像的效果相比，信噪比明显优于硬阈值和软阈值算法。硬阈值数据与设计数据基本相同，但对图像细节的保护明显优于重阈值。

从图1可以看出，这三种算法具有不同的去噪效果。三次去噪后图像信噪比（SNR）增加，因为检测后恢复的图像噪声成分减少，从而提高了信噪比（SNR）。但是，通过视觉影响比较图片，严重阈值算法的视觉效果最差，软阈值算法的视觉效果更详细，最好的视觉效果是本书中的算法，这是因为阈值算法是一个固定值；在小波域中，一般图像的所有部分，其系数大于或小于被去除的阈值。然而，图像本身在波长中的某些系数也超过或小于阈值，导致图像在重建过程中出现失真、大量细节丢失、突变或振荡以及图像不透明度。软阈值算法采用局部阈值去噪，在小波域中，去除图像各部分的噪声因子，尽可能多地保留图像系数的分量。然而，渲染每个分量的系数不均匀，导致在退出后去除不完整的噪声因子，导致退出后图像的低信噪比（SNR）；由于重建图像边缘的视觉效果导致连续波系数偏差较大，因此图像模糊。这样，噪声系数和图像系数可以分离，重建后的图像具有良好的视觉效果，信噪比（SNR）较高，排除了图像边缘不透明度的视觉效果。

与上述三组图像相比，该算法得到的信噪比明显高于硬阈值和软阈值算法，相应的色散值也较低。

3 结论

本设计主要研究一种基于尺度的自适应波形算法。首先，分析波形系数并基于尺度设置阈值。与小波域的软阈值和硬阈值方法相比，本设计基于现有算法，通过去除噪声和保持图像细节，实现了更好的节点，具有较高的实用价值。通过matlab7.0软件，将操作过程和算法结果形象地展示出来，并且与传统算法相比，其优势更加突出。