高温高产井油管屈曲对特殊螺纹性能的影响

刘祥康, 杨建, 杜明海, 丁亮亮, 刘欣洁, 李玉飞, 周浪

(1.中国石油西南油气田公司工程技术研究院， 成都 610017； 2.中海油田服务股份有限公司钻井事业部， 天津 300452； 3.西南石油大学机电工程学院， 成都 610017)

如今，中国油气开采已逐步迈向更深领域，井下结构受到更恶劣工况的严峻挑战。油管作为井筒完整性的一关键屏障，其正常工作是实现油气正常开采的重要保障，而油管接头作为机械连接结构，在生产中相较于管体更容易发生破坏，油田中由于接头问题导致的管柱失效比例达到90%[1-3]。为解决这一矛盾，许多厂家研发了种类繁多的特殊螺纹接头以代替传统API(American Petroleum Institute)接头，特殊螺纹接头相较于API接头增加了密封面与扭矩台肩，使得其密封性能更好，连接强度更高，采用特殊螺纹接头的油管在深井超深井、高压油气井、热采井等井下的复杂工况下表现出了良好的工作性能，取得了较好的应用效果。

近年来，中外学者针对特殊螺纹开展了大量的研究。Fen等[4]对特殊螺纹的变锥面及弧面/锥面两种密封结构的密封性能进行了对比研究，获得了两种密封型面密封性能的规律。Ernen等[5]开展了特殊螺纹金属对金属气密封性能模拟实验，分析了影响金属气密封性能的因素。刘奔等[6]设计了一种铝合金油管特殊螺纹及其配套使用的密封部件用于酸压作业，并分析了该接头不同位置的接触压力。曹银萍等[7]基于Petroleumandnaturalgasindustries：proceduresfortestingcasingandtubingconnections(IOS/TC 13679—2002)B系载荷包络线范围对某特殊螺纹进行了系统的仿真模拟，发现包络线范围内弯曲载荷对特殊螺纹的性能影响较大。张颖等[8-9]针对特殊螺纹密封性能开展了数值模拟评价研究，并提出了优化特殊螺纹气密封结构的方法。韩婷等[10]对双粗糙表面施加压力模拟油管螺纹密封面接触过程，获取不同压力下接触界面超声回波信号，分析频谱特征参数与接触应力大小的关系。王建东等[11]开展了一种气密封特殊螺纹密封完整性分析的管柱三轴设计系数研究，确定了高温和室温两种环境下螺纹安全适用包络线载荷范围及合理的三轴安全系教。闫龙等[12]利用有限元模型分析弯曲载荷下特殊螺纹接头的结构、密封及抗疲劳性能，并详细说明了相关评价方法。窦益华等[13]在考虑接头螺旋升角的情况下，应用有限元分析软件模拟特殊螺纹接头整个上扣动态过程，考虑在最大、最佳、最小扭矩作用下，分析特殊螺纹油管接头的密封性能。

上述研究借助实验以及有限元方法，研究了特殊螺纹在上扣以及复杂工况下的连接性能以及密封性能，为特殊螺纹的研究提供了很好的思路。但存在两点不足：一是许多研究内容中的复杂工况下研究只包含了内压、外挤以及轴向载荷而忽略了恶劣工况下相当突出的油管屈曲问题；二是许多专家学者在研究过程中大多建立二维轴对称模型进行分析，此模型在运算效率以及简单工况下的模拟优势明显，但难以对弯曲工况进行模拟。为此，建立某特殊螺纹的三维有限元模型，考虑高温高产井中温度、内压、轴向载荷与屈曲情况，对此特殊螺纹的连接性能与密封性能进行分析。研究成果对实际现场油管柱完整性及正常生产作业具有一定的指导意义。

1 油管柱屈曲及特殊螺纹性能评价理论

1.1 油管柱屈曲理论

在高温高产井生产过程中，由于井口位置以及底部封隔器对油管产生一定约束作用，使得井筒油管因自重、内外压力、温度以及管内流体摩阻等作用引起的变形并不能得到有效释放，进而造成井筒管柱处于压缩状态。当油管压缩轴向力达到临界屈曲载荷时，油管会发生一定屈曲现象。根据带封隔器油管柱各中效应所产生的轴向位移量，最终可得油管柱综合变形位移为

ΔL=ΔL1+ΔL2+ΔL3+ΔL4+ΔL5

(1)

式(1)中：ΔL1、ΔL2、ΔL3、ΔL4、ΔL5分别为活塞效应、鼓胀效应、温度效应、摩阻效应及螺旋屈曲效应作用下油管柱所产生的轴向位移量。

1.2 特殊螺纹性能评价理论

特殊螺纹性能评价包括两个部分：一是连接强度，通过评价整个接头Mises的应力分布、是否出现塑性贯通来实现，评价标准为此接头材料的应力应变曲线，如图1所示；二是密封性能，特殊螺纹主要依靠主、辅助密封结构保证密封性能，密封能力取决于每种负载条件下的金属对金属密封区域上的接触压力的大小与分布。

管内流体通过金属密封区域微小间隙的流动阻力可表示为

ΔR∝ΔLmin/S

(2)

式(2)中：ΔR为流体通过微小间隙流动阻力，N；ΔLmin为泄漏路径最小长度，mm；S为微小间隙的横截面积，mm2。

增大金属密封区域的接触压力可增大泄漏阻力，有效增强特殊螺纹的密封能力，产生的泄漏阻力可表示为

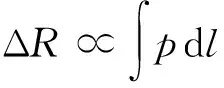
(3)

式(3)中：l为泄漏路径长度，mm；p为接触压力，MPa。

σys为屈服强度，MPa；σcs为强度极限，MPa图1 P110钢级油管材料应力-应变曲线Fig.1 Stress-strain curve of steel grade P110 tubing material

2 生产过程油管柱屈曲特性及受力分析

为了开展屈曲工况对油管特殊螺纹的性能影响研究，首先需对油管的屈曲情况进行分析。以塔里木区块某超深气井为例，其井筒管柱结构如表1所示。其中油管上封隔器位于井深6 250 m处，同时该油管柱组合处于196.85 mm生产套管内。通过计算得知，当产量为6×105m3/d时，井口温度为16 ℃，井底温度为152.67 ℃。在此工况下开展生产过程中井筒油管柱屈曲状态分析。

根据表1，利用ABAQUS软件建立油管柱屈曲有限元模型如图2所示，其中井口(A点)和封隔器位置(B点)全固定约束，并对油管柱上按照井筒温度梯度施加相应温度以及自重W，此外在井筒油管柱内外壁施加一定压力以还原生产过程中油压及环空流体对其产生的作用。通过对整体模型施加通用接触对，进而表征油管柱与套管柱在屈曲过程中所产生的接触作用。

图3为生产过程井筒油管柱屈曲横向位移俯视图，可以看出，此时井筒油管发生明显的屈曲现象。其中由于油管在x和y方向存在多个位置都与套管发生接触，进而证明在生产工况下部分井筒油管已产生了螺旋屈曲现象。

表1 井筒油管柱结构参数Table 1 Structural parameters of wellbore tubing string

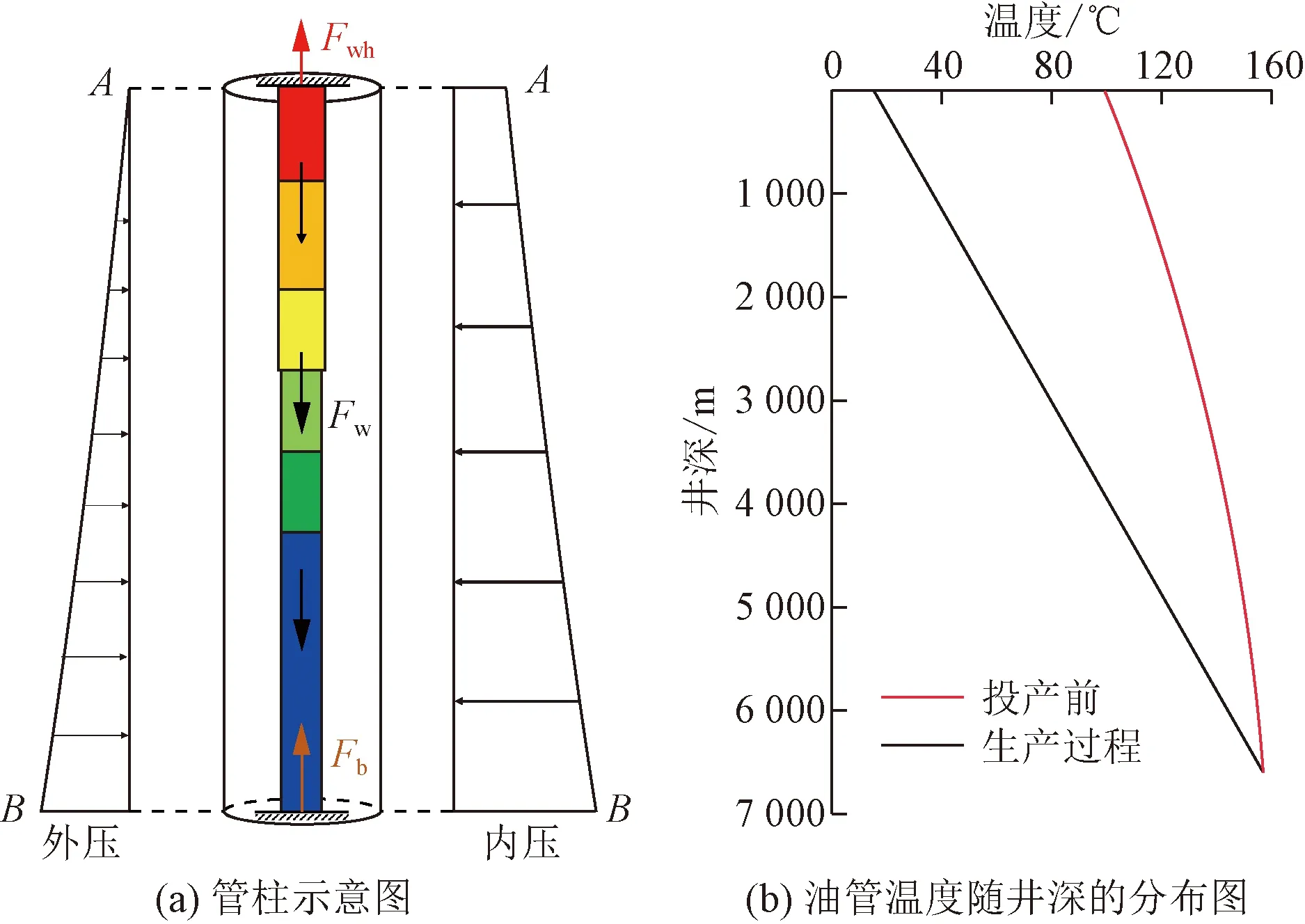
Fwh为井口端约束力，N；Fw为自重，N；Fb为井底端约束力，N图2 油管柱屈曲有限元模型示意图Fig.2 Schematic diagram of finite element model of tubing string buckling

为明确作业过程中不同井深位置下油管的屈曲状况，分别取出井筒油管柱在x和y方向位移沿井深分布曲线如图4所示。可以看出，井口至4 182 m井段油管柱并未发生屈曲现象，而下部管柱出现明显的屈曲现象，且随着井段加深，油管屈曲状态也随着发生相应改变，其中4 182～4 481.9 m井段油管只在y方向上产生明显位移，即发生正弦屈曲，4 481.9～6 000.3 m井段油管柱在x与y方向上都出现明显的位移，表明该井段油管发生螺旋屈曲，然而在6 000.3～6 250 m(封隔器位置)井段管柱屈曲状况发生改变，其只在x方向出现明显位移，进而说明井筒油管柱在x方向产生正弦屈曲现象。

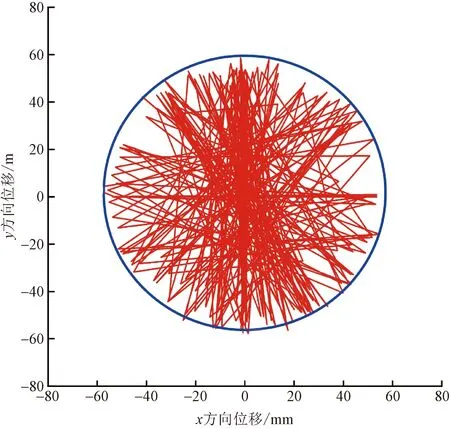
图3 井筒油管柱屈曲横向位移俯视图Fig.3 Top view of buckling lateral displacement of wellbore tubing string

图4 油管横向位移随井深变化关系Fig.4 Relationship between lateral displacement of tubing and well depth

在屈曲状况下，井筒油管柱会产生一定的弯曲，进而严重影响油管柱螺纹的连接强度及安全。图5为屈曲状况下井筒油管柱弯矩随井深分布曲线。可以看出，随着不同井段下管柱的屈曲状况不同，管柱上弯矩分布呈现明显差异。其中在4 182～4 481.9 m正弦屈曲井段管柱弯矩主要集中在x方向，其中最大弯矩可达到598.2 N·m，在4 481.9～6 000.3 m 井段管柱上弯矩在x及y方向上弯矩分布都相对均匀，其中最大点位于井深为5 620.72 m位置(B点)处，而在底部6 000.3～6 250 m正弦屈曲井段管柱上弯矩主要集中在y方向上，最大弯矩位于6 070.27 m处(C点)，为673.2 N·m。

3 屈曲状态下特殊螺纹有限元分析

基于所分析管柱的屈曲情况，对各屈曲段危险点处开展特殊螺纹连接强度及密封性能分析。特殊螺纹锥度为1∶16，承载面角度为-3°，导向面角度为10°，负扭矩台肩角度为-15°，密封形式为锥面-锥面，密封面角度为20°，以此建立三维有限元模型，采用C3D8R六面体减缩积分单元类型对模型进行网格划分，对螺纹啮合处，密封面过盈处，台肩处进行网格加密，得到公扣端网格数为104 016，母扣端网格数为148 200，网格划分如图6所示。

图6 特殊螺纹模型网格划分Fig.6 Mesh division of special thread model

3.1 正弦屈曲段危险点A处有限元分析

图7为油管沿x方向正弦屈曲段危险点A屈曲前后螺纹接头的Mises应力对比情况，在屈曲前，由于内压，轴向力与温度的综合作用，接头在台肩处的Mises应力较高，达到762 MPa；屈曲后，由屈曲所带来的弯曲载荷造成了接头环向上严重的应力分布不均匀，表现为弯曲载荷下受压一侧的台肩、鼻端以及管体大端第一对啮合齿上应力水平较高，其中台肩面靠近圆角处的Mises应力达到843 MPa，与台肩接触的鼻端末尾Mises应力达到887 MPa，大大超过了材料的屈服强度，受压一侧的台肩有失效的风险；另外，受拉一侧靠近接箍中心线的前两牙内螺纹的齿底应力水平也较高，达到699 MPa。

图7 A点处屈曲前后Mises应力对比Fig.7 Mises stress comparison before and after buckling at point A

为明确显示油管屈曲对接头环向上的应力分布影响，提取屈曲前后台肩面一半长度处沿环向路径上的Mises应力及接触压力分布规律，对比结果如图8所示。可以看出，屈曲前，台肩面上Mises应力分布均匀，数值约为393 MPa；屈曲后，Mises应力沿环向增大，应力较大的一侧为压缩侧，应力较小的一侧为拉伸侧；压缩侧最大Mises应力值达到 784 MPa，相较于未屈曲前增长99.5%，已经发生塑性变形；拉伸侧最小Mises应力为58 MPa；接触压力的变化规律与Mises应力变化规律一致，屈曲前接触压力分布均匀，屈曲后压缩段的最大接触压力由 423 MPa 增加到996 MPa；拉伸端有6°圆心角的区域内接触压力减小到0，表明此时台肩中点处已经被拉开，不存在接触。

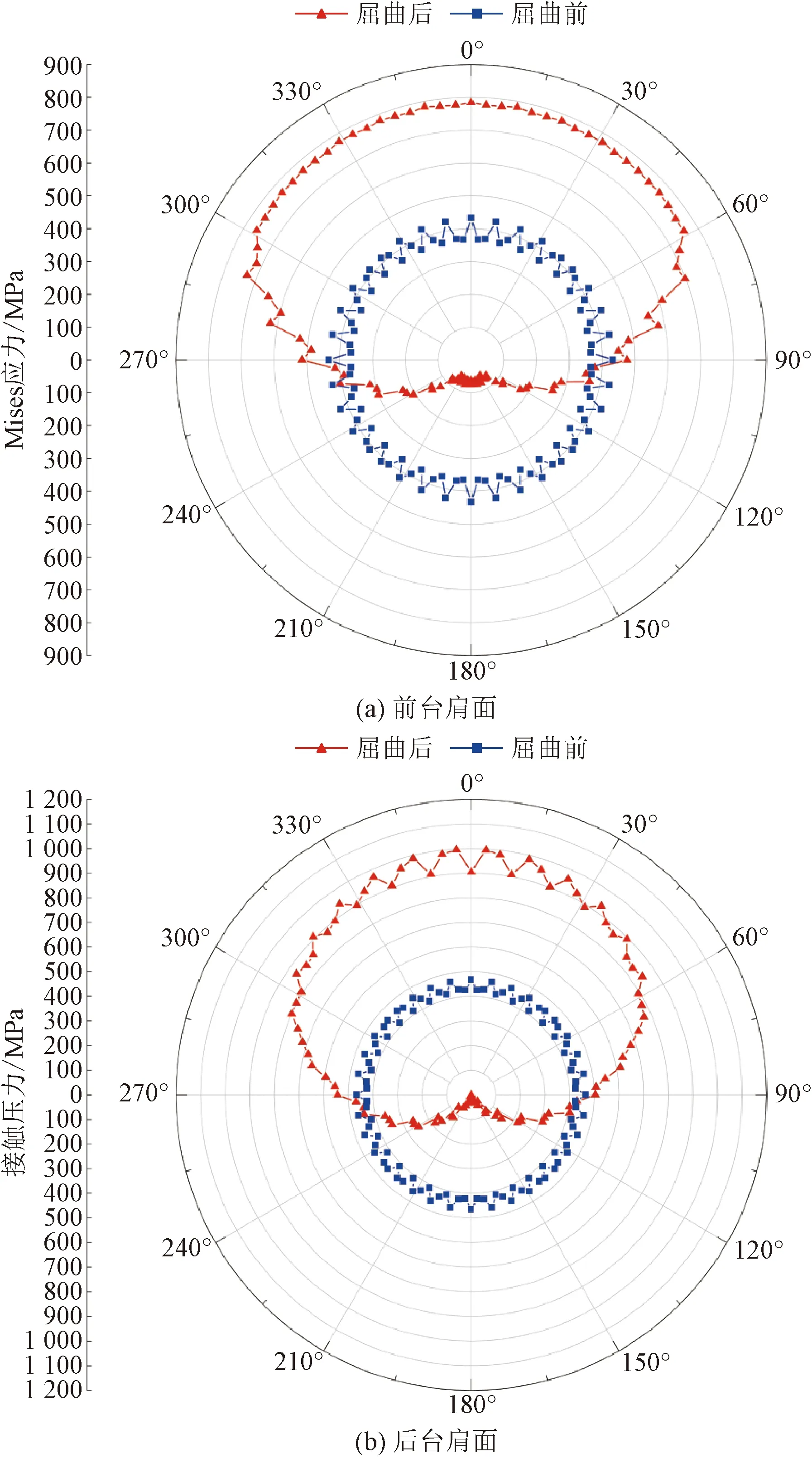
图8 A点处台肩面上Mises应力、接触压力变化Fig.8 Mises stress and contact pressure change on the shoulder surface at point A

3.2 正弦屈曲段危险点C处有限元分析

油管沿y方向正弦屈曲段危险点C屈曲前后螺纹接头的 Mises 应力对比如图9所示，相比于沿x方向正弦屈曲工况，此时弯曲载荷更大。螺旋屈曲前，由于内压，轴向力等复杂载荷的综合作用，接头在台肩处的Mises应力达到764 MPa；屈曲后，由屈曲所带来的弯曲载荷同样造成了接头环向上严重的应力分布不均匀，但沿y方向正弦屈曲段受压一侧特殊螺纹的应力集中更严重，其中台肩面靠近圆角处的Mises应力达到了864 MPa,与台肩面接触的外螺纹鼻端末尾上Mises应力为894 MPa，管体大端第一牙啮合处的Mises应力值达到880 MPa。

图9 C点处屈曲前后Mises应力对比Fig.9 Mises stress comparison before and after buckling at point C

屈曲后压缩侧台肩面1/2长度处环向路径上的最大Mises应力值为800 MPa，相比于未屈曲前增加了360 MPa，超过材料的屈服强度，发生塑性变形；拉伸侧的Mises应力水平较低，最小Mises应力值仅为70 MPa；压缩侧的接触压力明显高于拉伸侧接触压力，最大值为1 030 MPa，相较于未屈曲前对应点的485 MPa增加了112.3%；压缩侧接触压力为零的区域相较于沿x方向正弦屈曲工况下更大，有38°圆心角的区域内不存在接触。环向上的Mises应力分布及接触压力分布对比如图10所示。

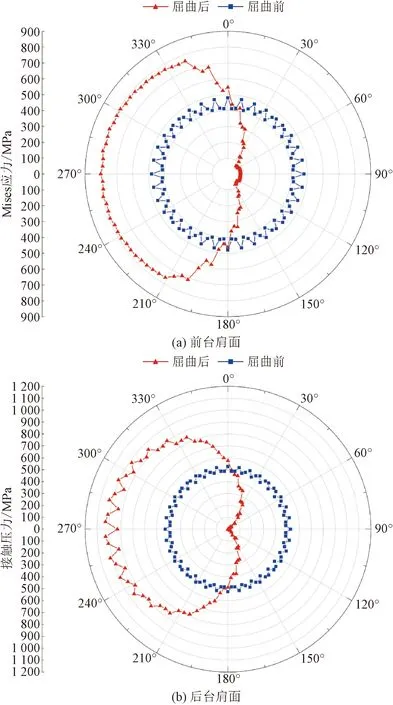
图10 C点处台肩面上Mises应力、接触压力变化Fig.10 Variation of Mises stress and contact pressure on the shoulder at point C

3.3 螺旋屈曲段危险点B处有限元分析

油管螺旋屈曲段危险点B屈曲前后螺纹接头的Mises应力对比由图11所示，屈曲前接头的Mises应力最大处仍然出现在台肩处，为764 MPa，螺旋屈曲后接头表现出与正弦屈曲段相同的应力分布特征：环向上应力分布不匀。但相比于正弦屈曲段单一方向上的弯曲载荷，螺旋屈曲段不同方向上的弯曲载荷一定程度上缓解了结构的应力集中现象，此时接箍台肩面上最大Mises应力值为 808 MPa，鼻端的最大Mises应力值为877 MPa，相比于正弦屈曲段有一定下降。

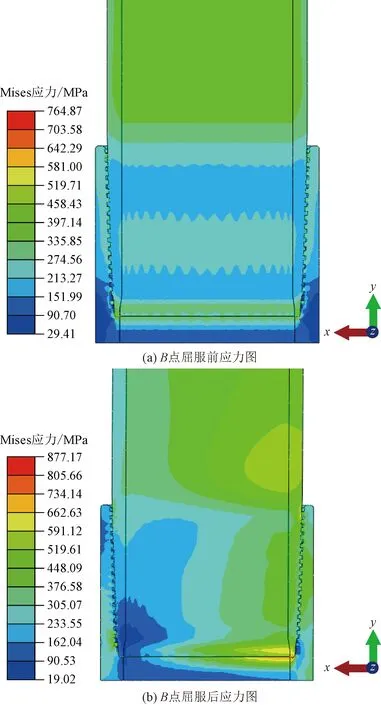
图11 B点处屈曲前后Mises应力对比Fig.11 Mises stress comparison before and after buckling at point B

螺旋屈曲段危险点C处台肩1/2长度环向路径上Mises应力及接触压力分布规律如图12所示。屈曲前后，压缩一侧的Mises应力由449 MPa升至769 MPa，接触压力由498 MPa升至940 MPa；拉伸一侧Mises应力由452 MPa降至64 MPa，接触压力由479 MPa降至26 MPa。

3.4 不同屈曲段危险点处接头密封性分析

由于不同屈曲段的特殊螺纹接头在油管屈曲后台肩面1/2长度的环向路径上出现了接触压力为零的情况，因此有必要对压缩端以及拉伸端的密封能力进行分析，沿锥度方向上提取不同屈曲段危险点屈曲后接头受压缩一侧密封面以及台肩面长度路径上的接触压力变化曲线如图13所示。

图12 B点处台肩面上Mises应力、接触压力变化Fig.12 Mises stress and contact pressure change on the shoulder surface at point B

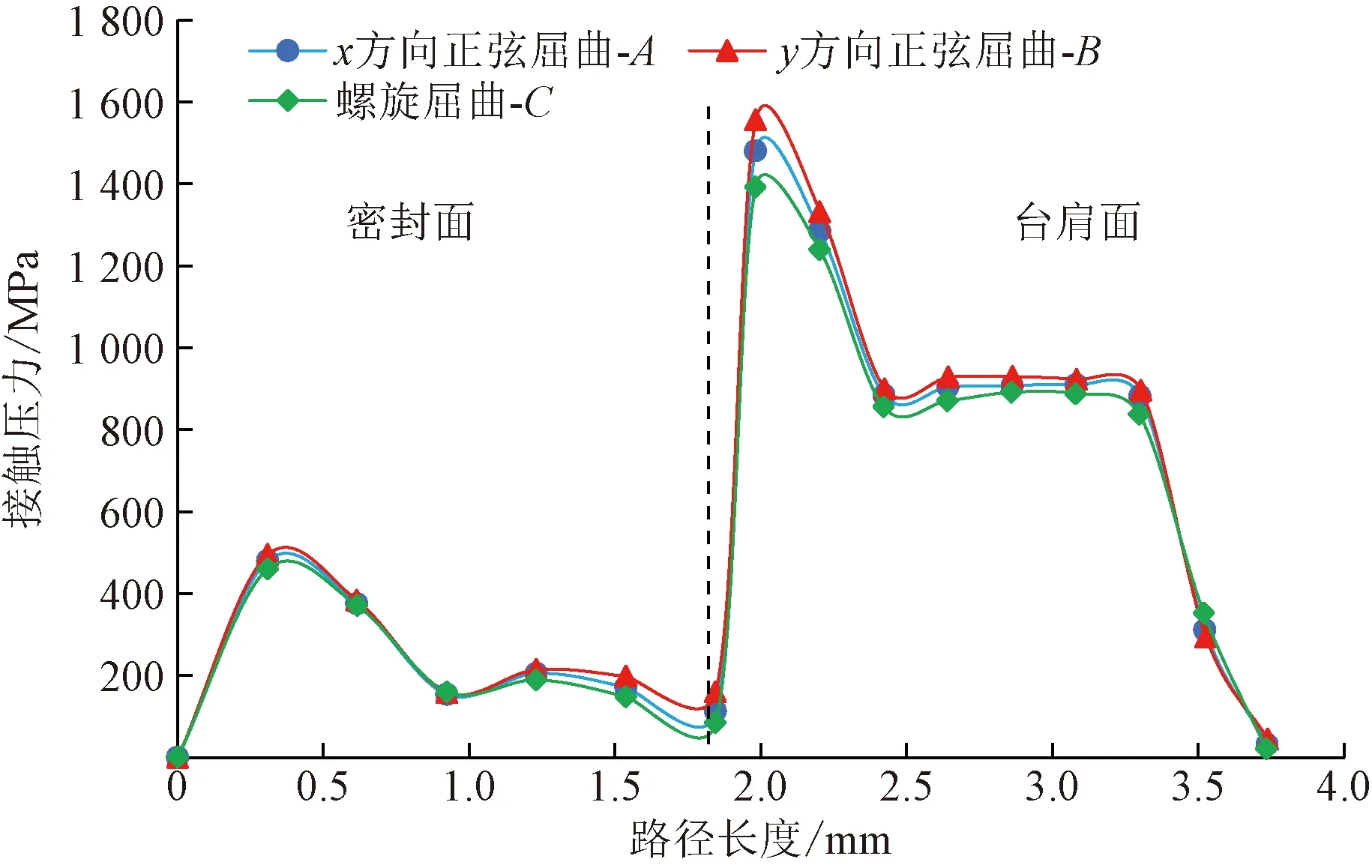
图13 危险点处接头压缩端接触压力变化曲线Fig.13 Change curve of contact pressure of the compression end of the joint at the dangerous point

由图13可知，压缩侧密封面与台肩面上的接触压力变化规律一致；受弯后，首先与鼻端接触的密封面上接触压力较大，之后呈下降趋势；由于负角度台肩角阻止鼻端在弯曲载荷的作用下沿着台肩路径向管子中心移动，使得靠近台肩圆角处的接触压力较大，而后接触压力慢慢下降，台肩面上的接触压力要明显高于密封面。3个位置的屈曲段危险点压缩端密封结构上的接触压力分布趋势一致，最大接触压力均位于鼻端在径向上最先与台肩面接触的位置，但正弦屈曲段路径节点上的最大接触压力分别为1 556 MPa(C点)、1 481 MPa(A点)略高于螺旋屈曲段1 392 MPa(B点)。

受拉伸一侧密封面以及台肩面长度路径上的接触压力变化如图14所示。可以看出，危险点A、C处接头拉伸一侧的密封面上接触压力均为零，主密封结构失去效用，其中C点台肩面上接触压力也为零，表明C点处接头主、辅助密封结构均失效；相比之下，螺旋屈曲危险点B处拉伸端密封面、台肩面上仍有接触压力，保有一定密封能力。

图14 危险点处接头拉伸端接触压力变化曲线Fig.14 Change curve of contact pressure of the tensile end of the joint at the dangerous point

4 结论

为研究高温高产井中油管屈曲对特殊螺纹性能的影响，分析了实际工况下的油管屈曲情况，并在此基础上，以某特殊螺纹为研究对象，建立了其三维有限元模型，分析了典型屈曲工况下特殊螺纹接头的连接强度与密封性能，得出如下结论。

(1)高温高产井中，油管处于复杂的井下工况，油管沿井深依次出现沿x方向正弦屈曲，螺旋屈曲，沿y方向正弦屈曲。

(2)油管屈曲对特殊螺纹接头的Mises应力、接触压力分布影响较大，具体表现为不同屈曲工况下，接头均表现出环向的应力分布不均，压缩一侧的Mises应力、接触压力较大，台肩以及管体大端的第一对螺纹啮合处的应力集中明显，Mises应力均超过了材料的屈服强度，台肩可能被压溃，螺纹牙可能折断；拉伸一侧较小。

(3)屈曲后受拉侧的密封面以及台肩面上的接触压力小，有效密封长度短，难以满足密封要求；井底正弦屈曲段危险点受拉侧的密封面及台肩面上的接触压力均为零，表明此时鼻端与台肩面已分离，密封结构失去密封能力。