波在分数Maxwell流体饱和孔隙介质界面的反射和透射

张秀娥， 康永刚

(防灾科技学院基础课教学部， 三河 065201)

研究弹性波在含流体孔隙介质中的传播，可以为油气储层、饱和及非饱和土、海底沉积物等介质的勘探提供理论基础。Biot[1-3]在建立该类介质波动方程时，首先分开考虑孔隙流体和固体骨架的运动，他的理论是该领域的开创性工作。之后被提出的重要模型有喷射流模型、Biot理论与喷射流相结合的(Biot squirt, BISQ)模型、饱和斑块模型、层状周期模型和双孔隙模型等[4]。这些理论都针对充满牛顿流体的孔隙介质，但实际孔隙流体经常表现出非牛顿流体特性，如油藏开发领域涉及的重油、页岩油、沥青油等高黏度原油[5]，当作牛顿流体计算的频散和衰减曲线，往往与实验结果存在较大的差距。Tsiklauri等[6]通过对黏滞系数引入一个修正因子，考察了弹性波在Maxwell流体饱和孔隙介质的频散和衰减特性。Cui等[7]在引入黏滞系数修正因子时，考虑了孔隙的尺寸分布。崔志文等[8]在BISQ模型中考虑了非牛顿流体的影响。Markov[9]研究了Maxwell流体饱和孔隙介质表面的Rayleigh波。Revil等[10]在研究震电效应时考虑了流体的非牛顿效应。刘文山等[11]使用动态黏度表征非牛顿流体的特征，但仍然是基于经典的Maxwell流体。Solazzi等[12]研究了弹性波在Maxwell流体饱和孔隙介质中传播时的喷射流效应。El Baroudi等[13]讨论了Maxwell流体饱和孔隙夹层中传播的洛夫波(Love wave)。以上研究表明，孔隙流体的非牛顿效应对弹性波的传播有重要影响。分数阶微积分已被成功应用到许多领域，如孔隙介质中的反常渗流[14]，但在孔隙介质的弹性波领域，相关研究很少。熊繁升[15]在建立孔隙介质波动方程时引入了分数阶导数描述的耗散函数。利用分数阶导数描述的分数Maxwell流体，更适合描述实际非牛顿流体的特征，但尚未发现在孔隙介质弹性波领域考虑该类流体的研究。

通过分析弹性波在含流体的孔隙介质界面上的反射和透射特征，可以获取该类介质的相关信息。Stoll等[16]、李尧等[17]研究了流体/流体饱和多孔介质界面上的反射与透射，应用了包含喷射流机制的BISQ模型。魏征等[18]、Sharma等[19]、Tomar等[20]研究了固体/流体饱和多孔介质边界上的反射与透射, 其中，魏征等[18]研究的是横观各向同性孔隙介质，而Sharma等[19]、Tomar等[20]考虑了孔隙介质含两种互不相容流体的情况。Wu[21]、代智军等[22]、Singh等[23]研究了液体饱和多孔介质/液体饱和多孔介质界面上的反射与透射, 其中代智军等[22]采用了双孔隙模型。还有学者研究了弹性波在含孔隙介质复杂结构的反射和透射，如三明治结构液体/孔隙介质/固体[24]、固体/孔隙介质/固体[25]等。以上研究认为，孔隙介质充满牛顿流体，目前尚未发现在反射和透射现象中考虑非牛顿流体的情况。

含流体的孔隙介质为耗散介质，传播的一般是非均匀波，目前的研究都基于均匀波，与实际情况并不符合。研究弹性波在孔隙介质界面反射和透射时，会采用Snell定理，即各列波在x方向(假设x方向在入射面内且沿着分界面)波数相等。基于均匀波假设，应用Snell定理会给出复数的三角函数和角度，物理意义不明确。例如，波由弹性介质射向孔隙介质时，入射角和入射波在x方向波数均为实数，由于孔隙介质中波数为复数，要求透射角的正弦为复数(即透射角为复数)，来保证二者乘积为实数。

鉴于此，通过对分数Maxwell流体在圆管内的振荡流分析，给出黏滞系数修正因子，由此来表示非牛顿流体对孔隙介质弹性波的影响。推导了波从弹性固体射向孔隙介质时，在两个半空间分界面的反射和透射系数。按照非均匀波讨论，给出的透射角为实数，物理意义明确。通过数值算例，并与牛顿流体的情况对比，讨论了孔隙流体非牛顿效应对反射和透射系数的影响。最后部分给出一些重要结论。

1 控制方程

1.1 Biot理论

Biot理论给出的流体饱和孔隙介质的应力-应变关系为[3, 16]

τij=(H-2μ)eδij+2μεij-Cζδij

(1)

pf=Mζ-Ce

(2)

H=(1-Kb/Kr)2M+Kb+4μ/3

(3)

C=(1-Kb/Kr)M

(4)

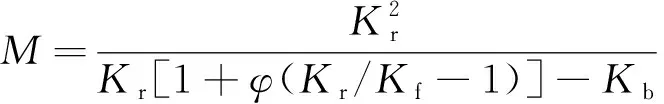
(5)

式中：Kb、Kr和Kf分别为骨架、固相和孔隙流体的体积模量。

Biot理论给出的运动方程为

(6)

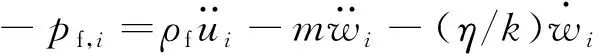
(7)

将式(1)、式(2)代入式(6)、式(7)，得到弹性波的动力学方程为

(8)

(9)

1.2 分数Maxwell流体的影响

当流体在圆管中流动，管壁按时间规律e-iωt沿纵向振动，其中，t为时间，ω为圆频率，i为虚数单位。对于柱坐标系(r,θ,z)，r和θ分别为极径和极角。流体只沿着z方向流动，vf为流速，vf为流速大小，即vf=vf(r,t)ez，其中ez为轴向的单位矢量。此时只有应力τrz不为零，动量方程为

(10)

考虑到物理量都按e-iωt规律随时间变化，式(10)可改写为

(11)

分数Maxwell流体的本构关系为[26]

(12)

当tm=0时退化为牛顿流体，当γ=1时为经典的Maxwell流体。保留式(12)中应变对时间的一阶导数，分数Maxwell模型才表现出流体的性质。分数阶导数有不同形式的定义，采用Riemann-Liouville定义，积分下限取为负无穷[27]，即

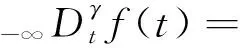
0<γ<1

(13)

当流体在圆管中流动，管壁按时间规律e-iωt沿纵向振动，式(12)变为

(14)

式(14)中：τrz为管壁应力。

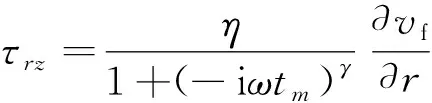
(15)

引入相对速度v1(r,t)=vf(r,t)-vs，其中vs为管壁的速度。将式(15)代入式(11)得

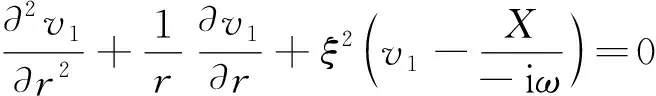
(16)

式(16)中：

(17)

ξ2=iωρf(1+(-iωtm)γ]/η

(18)

令a为圆筒半径，由非滑移边界条件v1(a,ω)=0，得

(19)

式(19)中：J0为零阶贝塞尔函数。

仿照Biot[2]的做法，圆管截面的平均流速可表示为

(20)

式(20)中：J1为一阶贝塞尔函数。

将式(19)代入式(15)得管壁的应力为

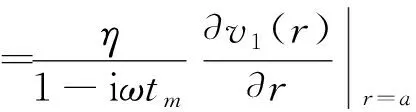
(21)

计算总摩擦力与平均流速的比值

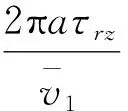
=-8πηF(κ)

(22)

(23)

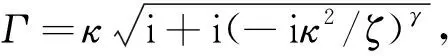
当γ=1时，式(23)退化为Tsiklauri等[6]的结果。分数阶导数模型，多了参数γ，相对于经典的Maxwell模型，更适合对实际非牛顿流体的描述。由式(22)可知，为了表示孔隙流体的非牛顿效应，只需用F(κ)η代替η。

由此，式(9)变为

(24)

为了求解式(8)和式(24)，对位移进行亥姆霍兹分解

(25)

(26)

式中：φ和ψ分别为标量势和矢量势；下标s为固体骨架；下标f为孔隙流体。

将式(25)、式(26)代入式(8)和式(24)，可求得快纵波波数lp1、慢纵波波数lp2和横波波数ls，具体求解过程可参考文献[16]，在此不再赘述。可求得流体与骨架势函数的幅值比

(27)

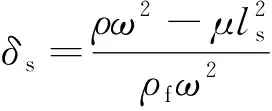
(28)

式中：δp1、δp2和δs分别为流体中P1波、P2波和S波与骨架中相应波的幅值比。

式(27)和式(28)说明同一种波在骨架和流体中引起不同幅值的振动，印证了Biot关于流体与骨架间存在相对运动的假设。

2 反射和透射

弹性固体半空间的弹性波控制方程为

(29)

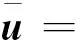
(30)

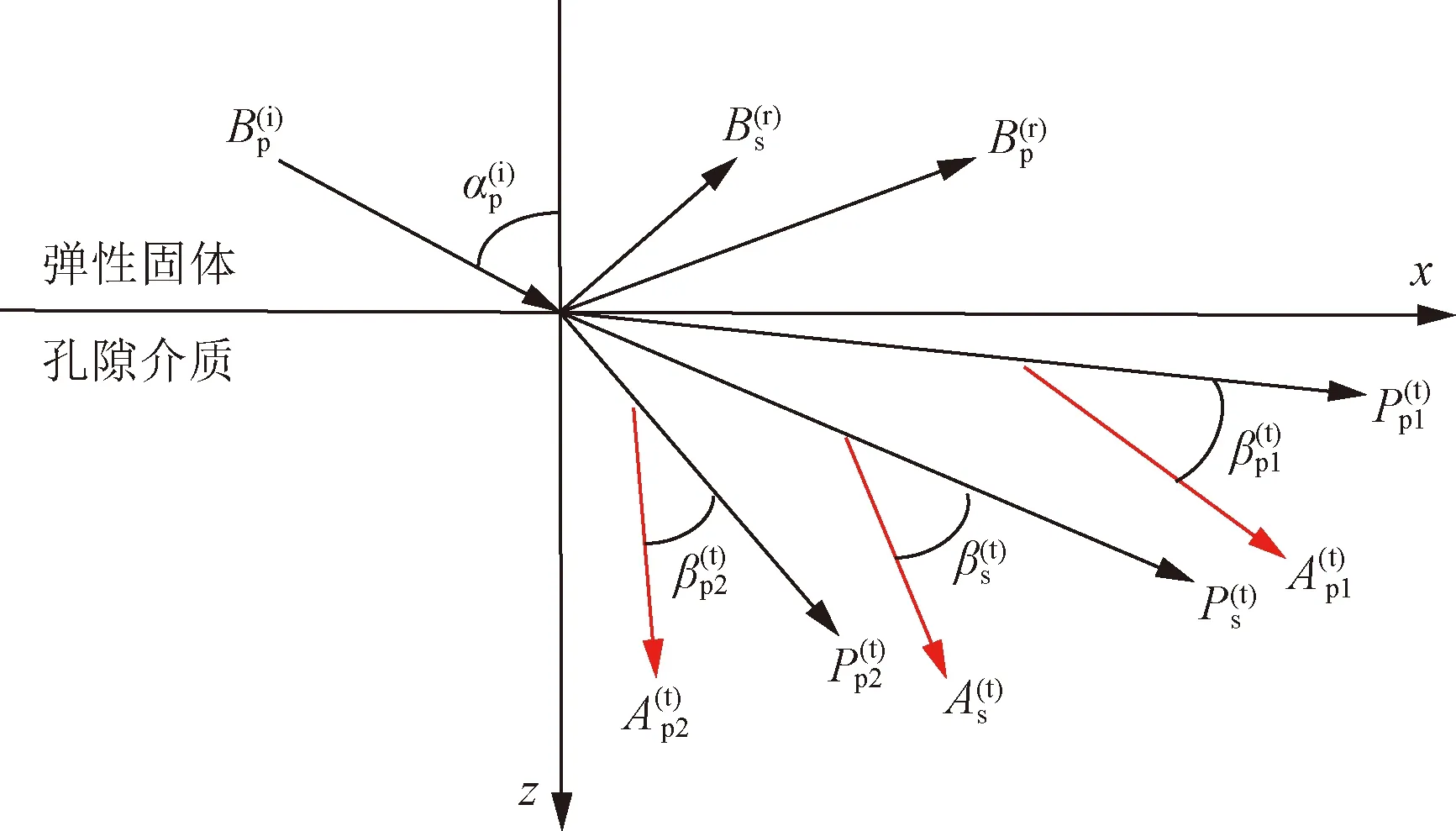
P为传播矢量；和分别为P1波、P2波和S波的透射角；A为衰减矢量；β为传播矢量与衰减矢量间的夹角；即上标i、r和t分别表示入射波、反射波和透射波；下标p、s、p1和p2分 别表示P波、S波、 快纵波(P1)和慢纵波(P2)图1 波在弹性固体/孔隙介质界面的反射和透射Fig.1 Reflection and transmission of elastic waves at an interface between solid and porous medium

式(30)中：φ1和ψ1分别为标量势和矢量势。

P波和S波的波数分别为

(31)

2.1 反射和透射波的势函数

弹性固体中的入射波和反射波用势函数可表示为

(32)

(33)

式中：B为幅值；上标i和r分别为入射波和反射波；下标p和s分别为P波和S波；矢量势ψ1=ψ1i2，其中，ψ1为其大小，i2为沿y轴方向的单位矢量。

考虑流体和固体相对运动的孔隙介质是耗散介质，传播的通常是非均匀波。目前，研究者们常按均匀波处理，与实际不符。此外，按均匀波处理，应用Snell定理会给出复数的角度，物理意义不明确。假设孔隙介质中传播的是非均匀波，则透射波用势函数可表示为

(34)

(35)

(36)

(37)

式中：B为幅值；上标t为透射波；下标p1和p2分别为快纵波和慢纵波；矢量势ψs=ψsi2，ψf=ψfi2，ψs和ψf分别为ψs和ψf的大小；位置矢量r=xi1+zi3，其中单位矢量i1和i3分别沿x轴和z轴方向。

传播矢量和衰减矢量可分别表示为

j=p1,p2,s

(38)

式(38)中：kj=kjR+kjIi和dj=djR+djIi分别为x、z方向的复波数，下标R和I分别表示实部和虚部，kj和dj满足：

(39)

注意dj取复数平方根的主值，即djR≥0。利用传播方向和衰减方向的夹角β，x方向的复波数可表示为

(40)

由Snell定理可知，各列波在x方向的波数相等，即

(41)

(42)

2.2 边界条件

在界面z=0的连续性条件如下。

(1)弹性固体和孔隙介质骨架的法向位移连续，可表示为

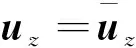
(43)

(2)对于非渗透界面，流体相对骨架的z方向位移为零，即

wz=0

(44)

对于渗透界面，有

pf=0

(45)

(3) 弹性固体和孔隙介质骨架的切向位移连续，可表示为

(46)

(4) 弹性固体和孔隙介质的正应力连续，可表示为

(47)

(5) 弹性固体和孔隙介质的切向应力连续，可表示为

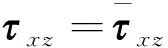
(48)

利用波的势函数式(32)～式(37)和边界条件式(43)～式(48)，反射和透射系数可由式(49)获得

(49)

式(49)中：a为一个5×5的矩阵；b为一个列矩阵；上标T表示转置矩阵。

式(49)中矩阵a的各元分素别为：

a13=-dp1,a14=-dp2,a15=-ksR。

对于不可渗界面有：a21=0,a22=0,a23=-δp1dp1,a24=-δp2dp2,a25=-δsksR。

对于可渗界面有：

矩阵b的各元素分别为：

3 数值算例和讨论

图2为德博拉数取值不同时，反射和透射系数随频率的变化曲线。低频时，非牛顿效应对反射和透射系数几乎没有影响。随着频率的增加，非牛顿效应逐渐变得明显，反射和透射系数随频率出现幅值衰减的振动。德博拉数ζ越小，与牛顿流体情况差别越大，振动幅度也越大。随着德博拉数的变化，孔隙介质的性质改变，孔隙介质的固有频率相应变化。当激振频率接近固有频率时，透射系数增大，反射系数相应减少。例如，当德博拉数为0.1时，在1 000～10 000 Hz范围，孔隙介质存在多个固有频率。因此P波反射系数和P1波透射系数在该频率范围出现周期性振动。

图3为分数阶导数的阶数对反射和透射波的影响。随着阶数的增加，与牛顿流体的情况差别越来越大，并开始出现幅值衰减的振动。当γ=1时，即整数阶Maxwell流体时，幅值振动最明显。分数阶导数的阶数变化，孔隙介质的固有频率变化。当一定频率范围内存在多个固有频率时，每当激振频率接近固有频率，透射系数增大，反射系数减少，出现幅值随频率的振动。通过阶数的变化，可以实现牛顿流体到Maxwell流体的过渡，扩大了模型的适用范围。

图4为黏滞系数对反射和透射系数的影响。由于德博拉数ζ=a2ρf/(ηtm)，相应改变ζ表示其他参数不变。低频时，介质有足够的时间达到松弛状态，而高频时，介质来不及松弛。所以，低频和较高频时，黏滞系数的影响可以忽略。黏滞系数越大，开始由低频时的值向高频时的值变化的频率越大，似乎图形在向高频移动。振动的幅值也随着黏滞系数的变化而有所不同。在中间频率范围，图形随黏滞系数增加向高频的移动，反映了材料松弛时间随黏滞系数的变化。

图2 德博拉数不同时的反射和透射系数Fig.2 Reflection and transmission coefficients for different Deborah number

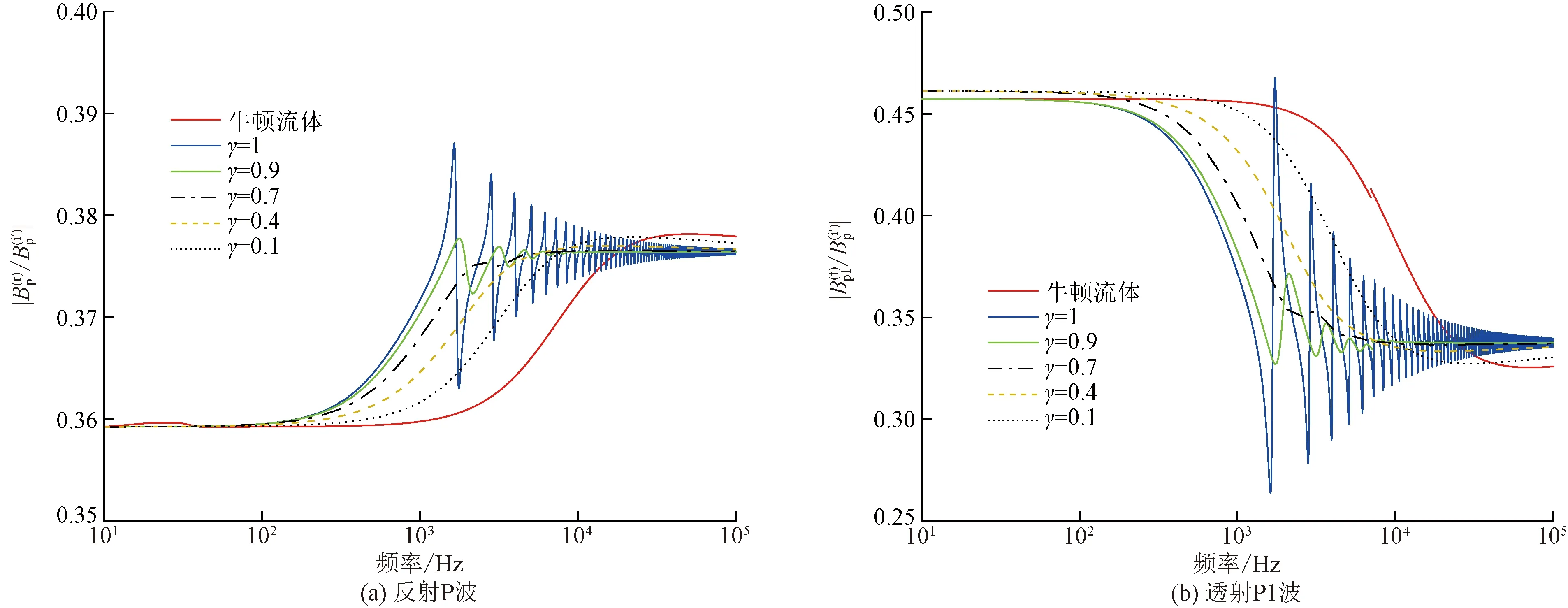
图3 分数阶导数的阶数对反射和透射系数的影响Fig.3 Influence of the fractional index on reflection and transmission coefficients

图4 黏滞系数不同时的反射和透射系数Fig.4 Reflection and transmission coefficients for different viscosity (γ=0.9,

图5为边界渗透性对反射和透射系数的影响。无论牛顿流体还是分数Maxwell流体，边界渗透性显著影响能量在反射波和透射波间的分配比例。边界可渗时，弹性波更易被反射。这是由于边界不可渗时，流体阻抗导致了透射波的增强和反射波的减弱。

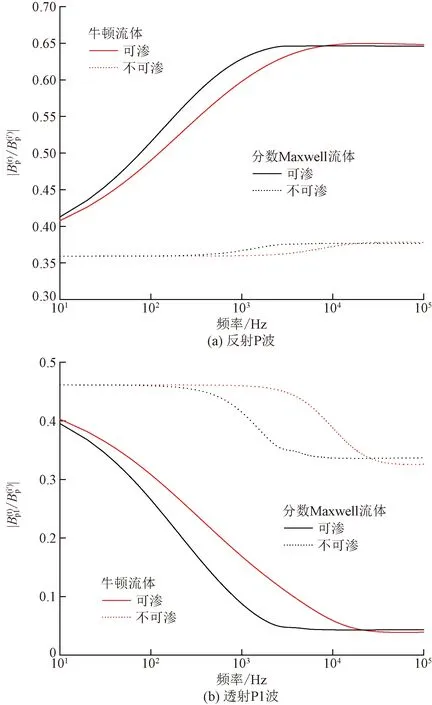
图5 边界条件对反射和透射系数的影响 Fig.5 Influence of the interface conditions on reflection and transmission coefficients (ζ=0.1, γ=0.6,

4 结论

通过对分数Maxwell流体在周期性振动圆管中流动的分析，给出黏滞系数修正因子，由此来表示孔隙流体非牛顿效应的影响。目前在孔隙介质弹性波领域常被讨论的Maxwell流体为其特例。推导了平面P波从弹性固体射向孔隙介质时，在界面的幅值反射和透射系数，其中孔隙介质充满分数 Maxwell 模型描述的非牛顿流体。按照非均匀波讨论，由Snell定理给出的透射角为实数，物理意义明确。通过数值算例，并与充满牛顿流体情况对比，研究了流体非牛顿效应对反射和透射系数的影响，得出如下主要结论。

(1)波在固体和孔隙介质的界面反射和透射时，孔隙介质中的快、慢纵波和横波都是非均匀波，它们的传播方向不同，但衰减方向相同，均垂直于界面。

(2)分数阶模型架起了牛顿流体与Maxwell流体间的桥梁，增加了一个参数，扩大了非牛顿流体模型的使用范围。

(3)德博拉数越小，分数Maxwell流体的非牛顿效应越明显，反射和透射系数与牛顿流体情况的差别越大。德博拉数较小时，由于孔隙介质固有频率的变化，会出现随频率的幅值衰减振动。

(4)黏滞系数、边界的渗透性对反射和透射波均有影响。虽然表现特征有差异，但都主要影响中等频率范围。