一类耦合交错的Hadamard型分数阶微分系统边值问题

张海燕，姚慧子

宿州学院数学与统计学院，安徽宿州,234000

由于分数阶微分方程具有整数阶微分方程所不具备的应用前景，其理论和应用研究受到科研工作者们的广泛关注，如Kilbas等[1]对分数阶微积分理论基础进行了系统总结，陈文等[2]介绍了分数阶导数扩散方程模型的理论基础、物理机理、数值算法，阐述了分数阶微分模型在地下含水层溶质迁移过程模拟、水工建筑物混凝土氯离子侵蚀，非饱和土壤水分运移过程分析与其他领域的应用，薛定宇[3]系统地介绍了分数阶微积分学与分数阶控制领域的理论知识与数值计算方法,Ahmad等[4]对一类特殊的Hadamard型方程的微分包含问题进行了深入研究，获得了一系列新成果。

近年来，分数阶微分方程解的存在性是数学研究者重点关注的问题，这方面有许多优秀成果[5-8]。特别地，在文献[9]中，Ahmad等讨论了具有边值条件的非线性交错的单变量Hadamard型微分方程：

(1)

通过利用Dhage不动点定理获得了方程(1)解的存在性结果。另一方面，分数阶微分方程的多变量耦合系统也具有重要的研究意义[10-13]，因为这类系统出现在许多交叉学科领域的应用中，如同步现象、非局部的热弹性学和生物工程等。

受上述文献启发，文本通过构建新的乘积范数空间，定义新的上模范数，在适当的非线性条件下，研究一类耦合交错的Hadamard型分数阶微分系统边值问题：

(2)

其中Dα1,Dα2是Hadamard型α1和α2阶的分数阶导数，fi∈C([1,e]×R×R,R{0}),gi∈C([1,e]×R×R,R)。当系统(2)退化为单个变量情形，则涵盖了文献[9]所讨论的交错Hadamard型微分方程；当fi退化为常数时，系统(2)为一般的耦合Hadamard型微分系统。因此，本系统推广和改进了文献[9]和文献[10-13]讨论的问题。

1 预备知识

定义实值函数f:[1,e]→R的函数空间X=C([1,e],R)。显然，空间X=C([1,e],R)是范数‖x‖=sup{|x(t)|:t∈[0,1]}下的Banach空间，也是乘积定义(x,y)(t)=x(t)·y(t)下的一个Banach代数。乘积空间=X×X在范数‖(x,y)‖=‖x‖+‖y‖下也是一个Banach空间，即范数线性空间(，‖(·,·)‖)是一个Banach空间，同时在乘积定义((x,y)·(u,v))(t)=(x,y)(t)·(u,v)(t)=(x(t)u(t),y(t)v(t))，t∈[1,e],下也是一个Banach代数。

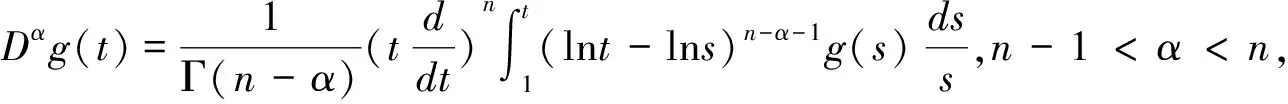
定义2函数g:(0,+∞)→R的α>0阶Hadamard型分数阶积分定义为

定义3[14]若X是Banach空间，称算子Τ：X→X是利普希茨的，如果存在一个常数LT>0使得 ‖Τ(x)-Τ(y)‖≤LT‖x-y‖,∀x,y∈X。

引理1[15](Dhage)设S是一个非空有界的Banach代数凸闭集,若算子Α：X→X和算子Β：S→X满足下列条件：

(C1)Α是利普希茨的，存在利普希茨常数LΑ;

(C2)Β是全连续的；

(C3)x=ΑxΒy⟹∀y∈S⟹x∈S;

(C4)LAMB<1,其中MB=‖B(S)‖=sup{‖Bx‖:x∈S};

则算子方程x=ΑxΒx在S中至少有一个解。

2 解的存在性

为获得系统(2)解的存在性结果，先给出下面引理。

引理2[4]令φ1，φ2∈C([1,e]×R×R，R)，则边值问题

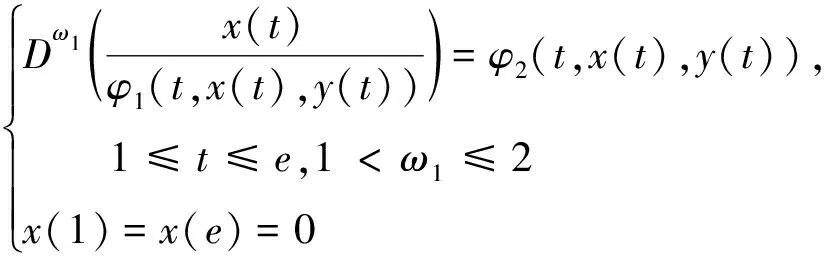
解的积分形式可表示为：

对于系统(2),列出下面假设条件。

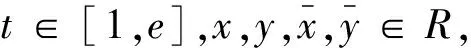
(H2)存在非负常数Mgi>0使得对任意t∈[1,e],x,y∈R,有|gi(t,x,y)|≤Mgi,i=1,2。

(H3)非负常数Lfi和Mgi，i=1,2，满足

定理1如果条件(H1)-(H3)满足，则耦合交错的Hadamard型分数阶微分系统(2)在[1,e]×[1,e]中至少存在一个解。

证应用引理1，由(2),我们取

(3)

(4)

S={(x,y)∈:‖(x,y)‖≤ρ}

(5)

则S是中非空Banach代数有界凸闭球。定义算子Α=(Α1,Α2):→和Β=(Β1,Β2):S→如下：

(6)

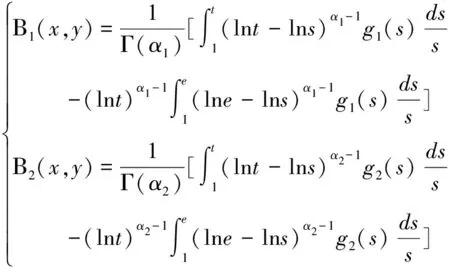
(7)

于是，微分系统(3)(4)和(6)(7)可以写成：

A(x,y)(t)B(x,y)(t)=(x,y)(t),t∈[1,e]

则有

(8)

下面分三步证明算子Α和Β满足引理1的所有条件。

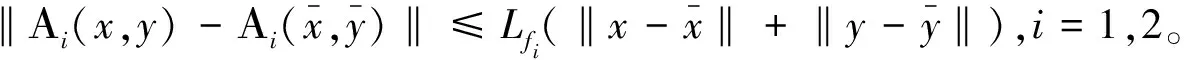
第二步，证明算子Β=(Β1,Β2)是从S到的一个即紧又连续的算子。

首先考虑算子Β的连续性，取(xn,yn),(x,y)∈S，且(xn,yn)→(x,y)，则由勒贝格收敛定理可知：

=Β1(x,y)(t),t∈[1,e]

同理可知：

因此，算子Β(xn,yn)=(Β1(xn,yn),Β2(xn,yn))在[1,e]上收敛于Β(x,y)，即算子Β是连续的。

接着，令(x,y)∈S，结合条件(H2)可知：

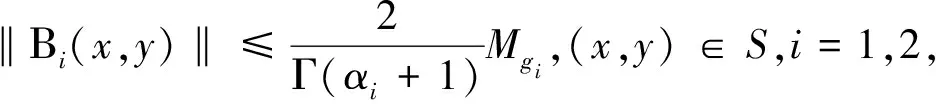
最后证明Β(x,y)是上的等度连续函数。令∀τ1,τ2∈[1,e],τ1<τ2，则

|Βi(x,y)(τ1)-Βi(x,y)(τ2)|≤

显然，当τ1→τ2时，对任意的(x,y)∈,|Βi(x,y)(τ1)-Βi(x,y)(τ2)|→0，即Βi(S)等度连续的。因此，Β(S)是等度连续的。

综上所述，Β(S)⊂是连续且紧的，由Azela-Ascoli定理知，算子Β在S中是全连续的。故引理1的条件(C2)满足。

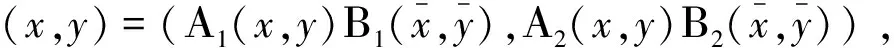
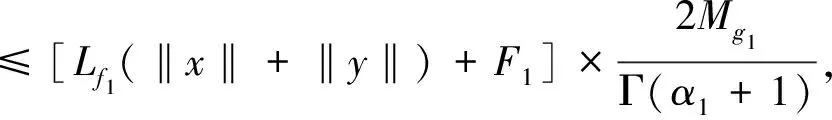
(9)

同理由(8)式第二个等式可知：

(10)

由(9)和(10)可知：

因为‖(x,y)‖=‖x‖+‖y‖，故对∀y∈S⟹x∈S。因此引理1的条件(C3)满足。

第四步,证明LAMB<1。由(H2)知

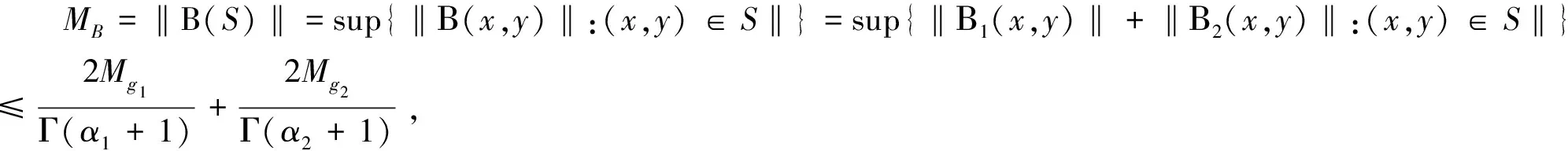
综上所述，算子Α和Β满足引理1的所有条件，因此由引理1可知耦合交错的Hadamard型分数阶微分系统(2)至少有一个解。

例1 考虑下列耦合交错Hadamard型分数阶微分系统:

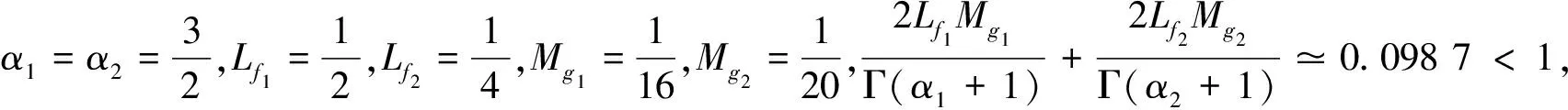
故由定理1可知耦合交错的Hadamard分数阶微分系统(2)至少有一解。