特征融合实现脑电信号情感分析

杨利英，孟天昊，张清杨，晁 思

(西安电子科技大学 计算机科学与技术学院，陕西 西安 710071)

情感是指一个人对客观事物是否满足自己的需要而产生的态度体验，是由人的大脑和生活经验两个方面共同决定的。积极的情感对个人的日常生活和身体健康都有益；反之，如果长期处于低落的精神状态，则很容易诱发抑郁症等心理疾病，严重者甚至会产生自残、伤害他人、轻生等损害身体健康的行为[1]。1997 年，由麻省理工学院 PICARD 教授定义了情感计算的概念[2]，从此情感计算正式成为现代计算机学科的一个分支。 情感计算可以通过人的表情、动作等外部生理信号进行分析，但由于情感具有可伪装和非瞬时性的特点，使得它们无法进行高精度的情感识别。脑电信号(Electro Encephalo Gram，EEG)是与情感相关的神经中枢产生的，能够体现出不同时刻的差异。生理和心理学家经过大量的研究，给出了合理、有效的情感评价标准[3]，也指出脑电与情感的关联性远远超过其他生理信号。

对于脑电信号特征提取，KHALILI等[4]首先提出提取脑电信号的平均值、方差、偏度和峰值等时域特征进行情感识别。郭柳君等[5]对采集的脑电信号采用两级脑控字符拼写范式及 DeepLDA 指令解码算法进行有效的目标字符解码，并提出一种结合深度线性判别分析的脑电信号分类识别算法。柳素红等[6]先分别提取脑了电信号的时域特征(Hjorth 参数 和 Energy)、STFT变换后的频域特征(Power、RASM 和 DASM)和经过小波变换后提取的时频域特征(Entropy 和 Energy)，然后分别对每个特征采用支持向量机评估其性能。ZHENG等[7]提取不同维度的脑电信号的判别特征进行情感分类，实验表明表现最优的是一阶差分、多尺度排列熵、gamma频带的能量和小波熵。马江河等[8]利用相空间重构技术提取了脑电信号和语音信号的非线性几何特征和非线性属性特征，并结合进行了计算。

在脑电信号特征选择方面，ZHANG等[9]使用C-RFE先根据权重对特征进行排序，选择出贡献度较高的脑电特征，运用最小二乘支持向量机分类，解决了脑电维数高的问题。XU等[10]提出了一种新的脑电特征选择算法——FSOR，该算法将过滤特征选择方法与封装特征选择方法相结合，使用了正交回归来寻找空间中的特征子集。ASGHAR等[11]利用最佳函数还原的反函数 BoVC 来提高脑电特征的质量。

针对脑电信号分类的研究，曹卫东等[12]直接将情感特征通过Softmax分类器将情感特征进行分类，输出情感极性。NAWAZ等[13]对比了分类方法SVM、KNN和DT，证明SVM在分类每种特征的效价和优势度方面明显优于KNN和DT，而在觉醒分类中，KNN在使用功率特征时略优于SVM，表明SVM在脑电信号情感识别上具有优越性。

对于特征提取和特征选择的综合应用方面，也有许多学者进行了探讨。LIU等[14]从时域、频域、时频域和多电极的角度提取了12种特征，总计组合特征维度达到1 952维。他们通过mRMR算法进行特征选择，分别使用KNN和随机森林(RF)作为分类器。从实验结果来看，mRMR算法明显地提升了准确率。在其实验中，RF分类器获得了比KNN好的效果。CANDRA等[15]将小波熵和平均小波系数(WEAVE)结合起来作为脑电信号情绪特征，使用归一化互信息(NMI)方法降维，并对Valence(非愉悦-愉悦)和Arousal(非激活-激活)情绪进行分类。SOROUSH等[16]提出了一种基于相空间动力学的方法对情绪进行分类，这种变换量化了相空间，并在新的状态空间中表示特征，称为庞加莱交叉点(Poincare intersections)特征。ISMAEL等[17]提出一种两步多数投票的方式来解决情感识别问题，第1步基于小波熵特征确定每一频段的最佳通道，第2步利用选出的所有频段的通道预测情感状态。

上述各方面研究都取得了进展，但是脑电信号分析在实际应用中还存在很多问题。一方面，由于脑电信号具有非平稳、信号微弱、频段差异大的特性，很难以相对简单的流程提取合理有效的特征来表征情感状态；另一方面，脑电信号需要多通道采集设备以保证与情感相关的信号都能被涵盖，而多通道采集设备在采集和数据处理过程中，存在大量对情感识别无意义或者贡献度很低的信息，这不仅使脑电信号处理的复杂度大幅提升，同时也会影响情感识别的精度。

针对脑电信号的固有特性，笔者在功率谱强度特征的基础上求得平衡功率谱强度特征，能有效地平衡脑电信号各频段的信息，有利于情感识别与分类。针对脑电特征冗余的问题，提出将Relief算法和mRMR算法进行融合，并设计新的性能评价机制对融合特征进行选择，最终获得能够更充分地表达脑电信号情感状态的特征向量，为后续进行情感分析识别提供了依据。

1 应用融合特征进行脑电情感识别

1.1 DEAP数据

DEAP(Dataset for Emotion Analysis using EEG，Physiological and video signals) 数据集由KOELSTRA等学者创建[18]。KOELSTRA团队从世界各地招募了32名受试者，其中男性和女性的数量各占总人数的一半，他们的年龄分布在19岁到37岁之间。在进行数据采集的过程中，首先让32名受试者佩戴好数据采集设备，然后观看了提前准备好的40个音乐视频，并在观看过程中采集受试者的生理信号。每一个受试者都要重复相同的实验过程40次，同时采集每次实验中受试者在不同的音乐视频刺激下的生理信号。这些生理信号是从受试者头皮上的40个通道上采集而来的，其中前32个通道采集的是脑电信号，后8个通道是心电、肌电和眼电等其他生理信号。

表1 DEAP数据集

在每次实验执行过程中，首先会显示目前所做实验的编号，即所对应的音乐视频的编号，然后会有3 s的空白，以使受试者的情绪恢复平稳。接着，是诱发情感的1 min 时长的音乐视频，诱发出的40个通道的生理信号被同期采集。依据效果评价和唤醒度所构成的二维情感模型[19]，在实验结束后让受试者对每一个视频的感觉在Valence(非愉悦-愉悦)、Arousal(非激活-激活)、Dominance(被支配-支配)和Like/Dislike(喜欢/不喜欢)这4个维度进行打分，分值的选择范围在1～9之间。为了适应情感识别问题的输入，DEAP将脑电数据降采样为128 Hz，情感刺激的时长为60 s，因此每一个通道有7 680个采样点。DEAP数据集的描述如表1表示。

1.2 平衡功率谱强度

由于脑电信号低频段与高频段的能量值存在很大差异，使用能量谱、功率谱等特征时，频谱的平方值会导致高低频段差异性被过度放大，不利于特征的分类与识别。针对这一问题，以能量谱密度为基础的差分熵特征[20]采取能量的对数值，对高低频段进行平衡，缩小了特征的差异性。功率谱强度[21]是对频域各样本点的幅值求和，相比于取平方的能量谱而言，它在平衡高低频段信号方面的效果更为显著。

为了综合利用高低频段的信号并避免二者差异过大，笔者在进行特征提取时采用基于功率谱强度(Power Spectrum Intensity，PSI)的平衡功率谱强度(Balanced Power Spectrum Intensity，BPSI)。首先将原始脑电信号划分成N个时间窗口；然后对每个时间窗口分别进行快速傅里叶变换；接着对频域采样点取幅值求和，得到功率谱强度；最后对功率谱强度取对数获得平衡功率谱强度。平衡功率谱强度的计算如下：

(1)

1.3 融合特征选择

对多通路脑电原始信号进行特征提取后，特征向量仍然存在较多冗余，特征选择旨在获得易区分真实情感的特征。特征选择主要有两种方法：一种是在特征集合内依据特征对相近样本的区分能力来选择特征，其代表为Relief算法[22]；另一种则在特征集合内选择彼此相关性较小而与输出结果相关性较大的特征，其代表为mRMR算法[23]。在应用方面，特征选择表现为以较少的特征提升或维持识别准确率。上述两种特征选择方法存在很好的互补性：Relief算法可以在保证准确率降低较小的情况下，较大幅度地减少特征维度；mRMR算法虽然能保持识别准确率，但降维效果有待提升。鉴于此，笔者综合两种算法，提出融合特征选择算法(Fusion Feature Select，FFS)。

首先，根据特征对相近样本的区分能力，将原始信号特征向量中的特征进行重排，得到新的特征向量VR。特征区分能力权值更新如下：

(2)

(3)

式(2)中，i为迭代次数；Ri是第i次迭代中从训练集中随机选择的样本；Wi(fl) 是第i次迭代中第l个特征的权重值；P(C) 指类别C在样本集中的占比；m为采样次数；r为最近邻样本个数；Hj是R同类样本中的最近邻样本，Mj是R不同类样本中的最近邻样本；ddiff(f，X1，X2)是样本X1与样本X2中的特征f的差异性，通过式 (3) 计算。式(3)中，v(f，X) 指的是样本X的特征f的特征值，max(f) 和min(f)分别代表所选样本的特征f的最大值与最小值。

其次，以特征集合彼此相关性较小而与分类标签相关性较大为标准，对原始特征重排，得到特征向量VM，评判标准如下：

maxΦ(D，R)，Φ=D-R。

(4)

式(4)中，D表示最大相关性，按式 (5) 计算；R表示最小冗余，按式 (6) 计算：

(5)

(6)

其中，I为互信息函数。

接着，通过特征向量融合式(7)，调整特征权重WR和WM，得到融合特征向量组G。G是二维特征向量，包含了多组融合特征向量。

G[i]=VRWR+VMWM，

(7)

其中，G[i] 表示第i个特征融合向量。第二维容量取决于WR和WM改变的次数，每改变一次，容量加1。改变的幅度由步长决定，步长的取值范围为 [0.01，1]。

最后，通过验证集在融合特征向量组G中选择最佳融合特征向量VBest和其对应的特征维度的数目NBest，应用融合算法完成情感识别。

1.4 度量机制

应用特征选择算法对特征向量进行降维的同时，要尽可能地提升或保持识别精度，这是特征选择的基本要求。为综合评价特征选择算法的性能，笔者提出一种度量机制——Score，其计算如下所示：

(8)

其中，S是特征所得分值；A表示识别准确率；N表示特征选择算法降维后的特征数目；C为度量代价的参数，用以表征特征维度对情感识别系统的负担。经过对DEAP数据集的多次实验，并调研使用DEAP数据集的其他研究者[20]的实验结果，设置 Cost 为25，作为代价取值。

1.5 算法验证

YAN等[24]指出，较小时间刻度的脑电信号能显示出更好的情感识别性能，同时指出时间窗大小设置为1～2 s时最优，因此笔者将60 s的脑电数据按每段一秒划分成60个片段，其中采样频率为128 Hz。随机选择1/6的片段作为测试集(400个片段)，1/6的片段作为验证集(400个片段)，剩余的4/6的片段作为训练集(1 600个片段)。为了验证平衡功率谱强度的性能，将平衡功率谱强度与包括功率谱强度、差分熵等在内的多种频域特征进行了对比实验。为验证特征融合算法的性能，采用支持向量机分类算法和高斯核函数，对脑电信号特征进行情绪状态的两类分类，比较了特征融合算法与包含Relief、mRMR在内的其他特征选择算法。

2 实验结果

2.1 平衡功率谱强度

表2列出了BPSI和PSI及其他常用频域特征的对比结果，包括能量谱密度(Energy Spectral Density，ESD)、功率谱密度(Power Spectral Density，PSD)、相对强度比(Relative Intensity Ratio，RIR)、差分熵(Differential Entropy，DE)。由表2可见，无论是在Valence维度上，还是Arousal维度上，BPSI都有明显优势。

表2 平衡功率谱强度与其他特征分类准确率对比 %

2.2 融合特征选择

以不进行选择的BPSI特征作为基线(Base)，比较了特征融合算法(FFS)、Relief和mRMR特征选择算法，其中Score数值由式 (8) 计算得到，结果如图1所示。

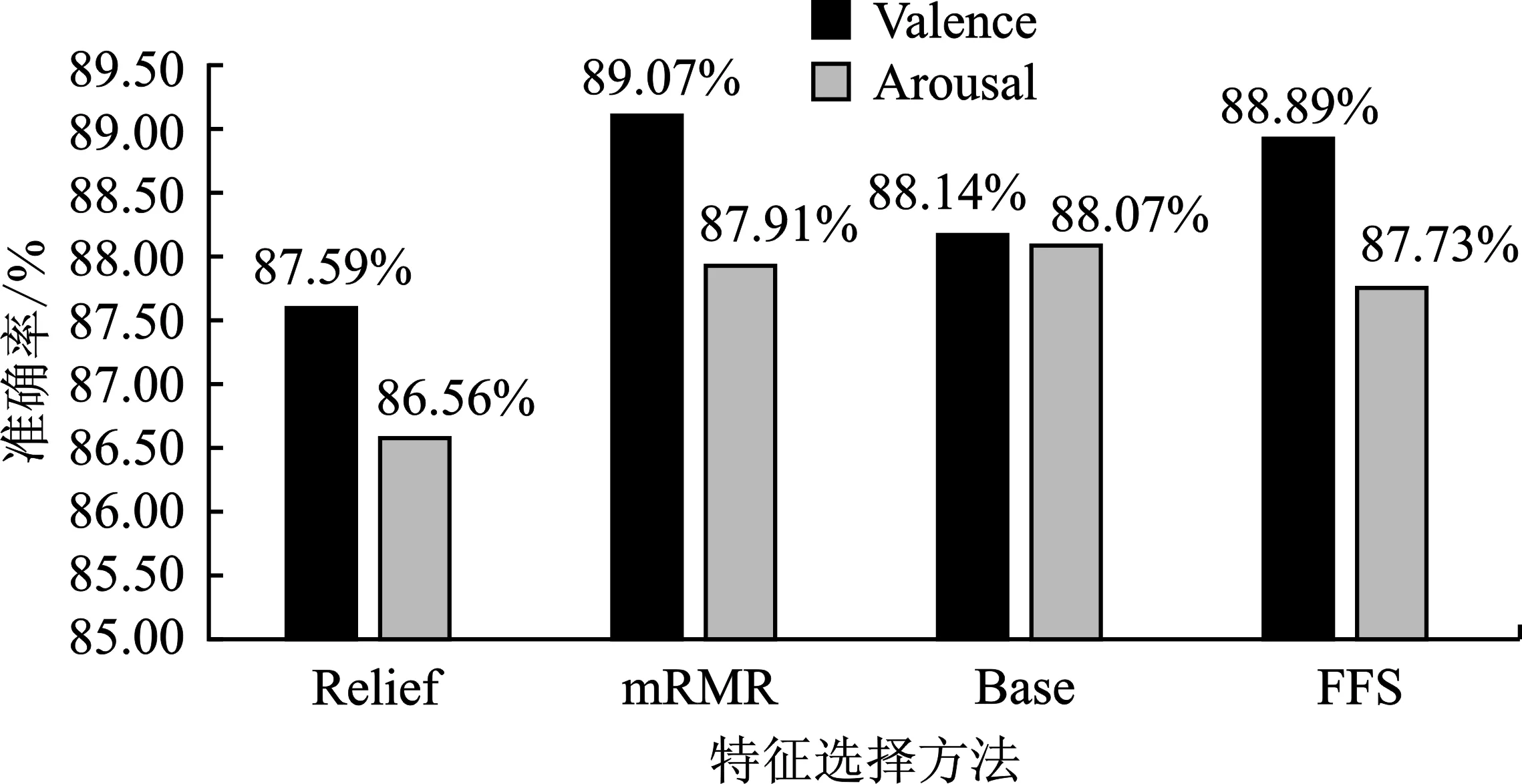
(a) 准确率

由图1可见，FFS在Valence维度上有86.26的Score分值，Arousal维度有85.02的Score分值，明显优于其他算法。两个维度上的Score结果都比传统特征选择算法中综合分值居首的Relief算法高出约2分，高出基线约3.9分。从准确率来看，FFS的准确率在Valence维度为88.89%，Arousal维度为87.73%，其平均值较基线有提升，且在降维方面有较大优势。同时，在两个维度上，FFS都明显优于Relief算法。从特征数目来看，FFS在Valence维度的特征数目为67，Arousal维度的为68，这比传统特征选择算法中最佳分值的Relief算法要低14维，相对于基线达到58%的降维，降维效果显著。由此可见，无论在识别精度还是降维效果方面，FFS算法都有好的表现。

2.3 情感识别方法比较

当前，许多学者在DEAP数据集上进行了特征提取和特征选择方面的研究。

笔者将引言中提及的应用于DEAP数据集的算法和笔者提出的融合算法进行对比，结果如表3所示。从表3可见，笔者提出的算法在准确率方面优于其他算法。

表3 DEAP数据集上情感识别方法准确率对比 %

3 分析及讨论

针对脑电信号情感分析识别率低、特征冗余的问题，笔者从特征提取和特征选择两个方面进行了探讨。

在特征提取方面，取频段幅值和的对数值，得到平衡功率谱强度(BPSI)，使各频段特征之间的差异远小于其他频域特征各频段的差异，以此提高后续分类能力。相比于PSI和BPSI，优势在于使一部分受试者的准确率有了较大幅度的提升，并且绝大多数受试者的BPSI特征的表现要优于PSI。这充分说明BPSI在脑电信号处理上有较强的普适性，有利于脑电情感的识别。与其他脑电信号频域特征相比，BPSI也有更好的识别效果，在一定程度上解决了脑电信号识别率低的问题。

在特征选择方面，提出了融合特征选择算法(FFS)。该算法从特征间能否区分近距离样本、特征集合能否彼此区分且与标签相关性较大这两个角度去选择特征集合。与基线、Relief和mRMR算法的实验对比表明，FFS算法选择的特征集合在特征数目上有较大优势，Valence维度的特征数目为67，Arousal维度的为68，相较于基线达到了58%的降维。FFS在识别准确率上也比基线高，兼顾了识别精度和降维效果；综合分数Score也显示出该方法的优越性。这说明对于存在互补性的多种特征选择方法，使用FFS算法能在扩大搜索空间的同时产生新的最优解，充分挖掘了各种算法的优势，在解决特征冗余问题的同时，提升了识别精度。

在情感识别方法的综合分析方面，将BPSI与FFS的组合方法和近年来在DEAP数据集上进行特征提取和选择的方法进行了对比。从结果来看，无论是识别精度还是降维效果，笔者所提出的方法都处于领先地位。但是，由于个体的特征集合不同，在应用特征融合方法进行情感分析时，仍需要采集全通道的脑电信号。

4 总 结

笔者从脑电信号的两个核心研究方向，即从特征提取和特征选择出发，改进PSI得到BPSI，并提出了特征融合选择算法。经实验验证，基于BPSI的特征融合选择算法在提高识别准确率的同时大幅度地降低了特征维度，有助于解决脑电信号情感分析时识别率低、特征冗余的问题。

下一步将对各受试者的最优特征集合进行研究，以获得针对脑电情感分析的公共通道信息，提高脑电信号的采集效率，并缓解计算和传输压力。