准最小最大优化动态输出反馈鲁棒MPC
平续斌,刘思伟,吴宗原,刘 鼎,李志武
(西安电子科技大学 机电工程学院,陕西 西安 710071)
模型预测控制(Model Predictive Control,MPC)为一种基于滚动时域优化的最优控制方法,其在每个采样时刻利用系统模型和量测信息对系统未来动态进行预测,并且在考虑物理约束以及满足性能指标情况下优化求解控制输入序列。但在当前采样时刻,MPC仅实施优化控制输入序列的第一个;在下一采样时刻,系统模型参数和量测信息得到更新且控制时域前移一步,然后重复上一时刻同样形式的优化控制问题[1]。因MPC能够处理包含物理约束系统的优化控制问题,从而得到了学术界和工业界的广泛关注[2-6]。然而在实际过程中,精确的模型参数往往难以获得且系统的真实状态或部分真实状态难以测量。对于实际过程中存在的未知系统状态、物理约束和建模不确定性情况,输出反馈鲁棒MPC不仅能确保标称系统性能,而且能够确保在模型参数以及干扰等不确定性情况下满足系统鲁棒性的稳定性要求[7]。
线性参数变化(Linear Parameter Varying,LPV)系统的动态特性依赖于时变的调度参数(Scheduling Parameter),并且处于线性子系统所构建的凸包集合之内,因此可以描述不确定性或者非线性系统,并且可借助线性系统中已有的成熟优化控制技术[8]。此外,当Takagi-Sugeno (T-S)模糊系统的前件变量(Premise Variable)等同于线性参数变化系统的调度参数时,两类系统等价[9]。针对线性参数变化系统的输出反馈鲁棒,MPC通常采取观测器和控制器综合设计方法,因为涉及到综合鲁棒状态估计和控制的问题,所以往往造成优化中双线性矩阵不等式(Bilinear Matrix Inequality,BMI) 形式非凸约束,从而难以在多项式时间内求解困难[10]。针对线性参数变化系统加有界干扰,以及T-S模糊系统加有界干扰形式描述的不确定性系统,文献[11-15]借助鲁棒正不变(Robust Positively Invariant,RPI)集合理论和线性矩阵不等式[16](Linear Matrix Inequality,LMI)技术研究了多种动态输出反馈鲁棒MPC方法。在文献[11-15]中,针对线性参数变化系统的调度参数或T-S模糊系统的前件变量精确已知情况,动态输出反馈鲁棒MPC控制器采用参数依赖形式,利用线性矩阵不等式技术,将在线非凸优化问题转化为凸优化求解。
针对输出反馈鲁棒MPC问题,通常考虑闭环系统鲁棒稳定进而确保被控系统的鲁棒稳定性,因此常涉及到闭环系统鲁棒正不变集合的构建和优化。文献[11-15]中在线输出反馈鲁棒MPC在每个采样时间采用常见的最小最大(Min-Max)优化的鲁棒优化控制形式,从而考虑到当前以及未来时刻所有可能不确定模型参数以及干扰情况,并且将当前和未来时刻的闭环系统状态约束在共同的鲁棒正不变集合之内,因此往往造成优化控制问题保守性。在文献[11-15]中,动态输出反馈鲁棒MPC优化问题未考虑当前时刻模型参数精确已知情况,而且参数依赖形式控制器造成优化问题中双凸组合[17](Double Convex Combination)约束,从而因引入了大量的线性矩阵不等式决策变量和约束,造成在线计算量大的问题。此外,针对包含模型参数不确定以及有界干扰,输出反馈鲁棒MPC通常会涉及到动态变化的估计误差集合界的问题,也会影响系统的控制性能、鲁棒稳定性和物理约束处理等。在文献[11-15]中,通过辅助优化,对估计误差集合的界进行更新,其中文献[11,14]中辅助优化可决定下一采样时刻主优化是否需要求解;文献[12-13,15]中辅助优化更新误差集合方法可确保主优化问题的递归可行性。文献[12-13,15]中估计误差更新可以基于闭环系统状态在鲁棒正不变集合内的不变性进行,但为了更进一步地降低估计误差集合保守性,在辅助优化中将通过闭环系统状态不变性获得的估计误差集合与估计误差系统获得的估计误差集合进行比较。然而在误差集合运算和比较过程中,往往因为集合运算操作而造成估计误差集合界更新保守性问题,从而降低系统控制性能以及影响系统鲁棒稳定性和物理约束处理。
不同于文献[11-15]中动态输出反馈鲁棒MPC方法,文中动态输出反馈鲁棒MPC采用了准最小最大(Quasi-Min-Max)优化,不仅可提升系统控制性能和确保优化问题递归可行性,而且可以降低算法的在线计算量。具体方法为当前时刻动态输出反馈控制器驱使闭环系统状态约束在鲁棒正不变集合之内,而通过未来时刻动态输出反馈控制器使得预测的闭环系统状态约束在非增的鲁棒正不变集合之内。此外,在优化当前时刻动态输出反馈控制器参数时,考虑到当前时刻精确已知系统模型参数,从而降低了优化控制问题的保守性。在主优化问题求解中,通过考虑干扰以及系统输出量测相关的模型参数为恒定矩阵情况,从而避免了双凸组合约束引入所造成的在线计算量大问题。此外,估计误差集合更新采用了预测的闭环系统状态的在鲁棒正不变集合内的不变特性,从而不仅降低了估计误差集合更新保守性,同时避免了辅助优化问题求解。
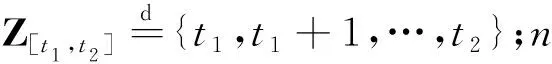
1 线性参数变化系统和物理约束
考虑如下具有有界干扰的离散时间线性参数变化系统:
x(k+1)=A(k)x(k)+B(k)u(k)+Dw(k),y(k)=Cx(k)+Ew(k) ,
(1)
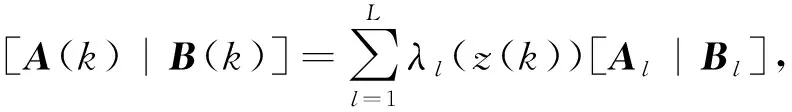
(2)
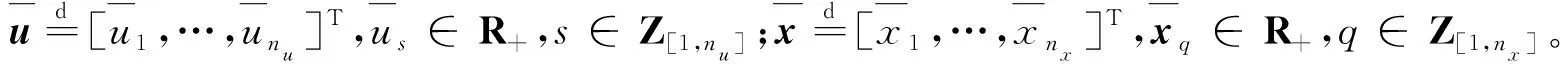
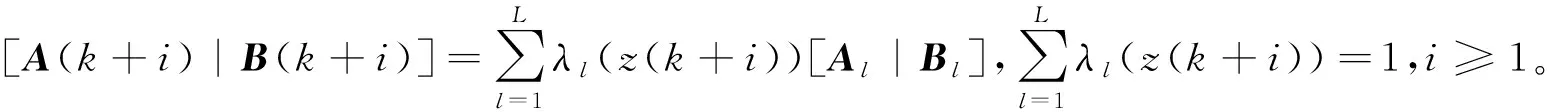
2 准最小最大优化动态输出反馈鲁棒MPC
2.1 动态输出反馈控制器和扩展闭环系统
对于式(1),设计动态输出反馈控制器为
(3)
u(i|k)=Cc(i|k)xc(i|k)+Dc(i|k)y(i|k) ,
(4)
(5)
其中,xc(i|k)∈Rnx,i≥0,表示控制器状态;{Ac(k),Bc(k)}和{Ac(i|k),Bc(i|k)},i≥1,分别表示当前和未来时刻的控制器增益矩阵;{Cc(k),Dc(k)}和{Cc(i|k),Dc(i|k)},i≥1,分别表示当前和未来时刻的反馈增益矩阵。考虑到式(1)中调度参数在当前时刻可获得,但在未来采样时刻不确定情况,设计上述动态输出反馈控制器式(3)~式(5),其中式(5)中动态输出反馈控制器参数{Ac(i|k),Bc(i|k)},i≥1,为参数依赖形式。利用式(1)和式(3)~式(5)获得如下扩展闭环系统:
(6a)
其中,
(6b)
在文献[11-14]中,针对当前和预测的扩展系统状态采用了相同参数依赖形式的动态输出反馈控制器。文中分别针对当前和预测的扩展系统状态,设计不同动态输出反馈控制器式(3)和式(4),而仅式(4)中动态输出反馈控制器采用参数依赖形式。
2.2 扩展状态约束
假定式(7)中M∈R2nx×2nx和Q∈R2nx×2nx为互逆矩阵,且M1∈Rnx×nx和Q1∈Rnx×nx为对称正定矩阵。令M2=-M1,则可得到式(8)
(7)
(8)
(9)
(10)
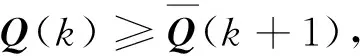
(11)
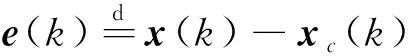
(12)
ρ(k)Me(k)≥M1。
(13)
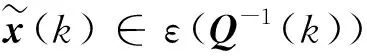
(14)
如果存在ρ(k)∈(0,1),使得式(15)和式(16)中控制器状态和估计误差约束同时满足,则式(14)中约束成立。
(15)
eT(k)M1e(k)≤ρ(k)eT(k)Me(k)e(k) 。
(16)
利用式(8)和Schur补引理,知式(12)保证式(15)成立,并且式(13)保证式(16)成立。
2.3 扩展闭环系统的鲁棒稳定性条件
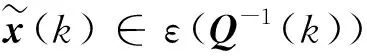
(17)
(18)
1-α1-α2≥0,1≥α1≥0,1≥α2≥0 ,
(19)
(20)
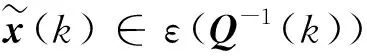
(21)
式(21)的充分条件是式(19)和式(22)同时成立:
(22)
对于式(6),式(22)的充分必要条件为
利用Schur补引理,式(23)等价于
(24)
定义如下矩阵:
(25)
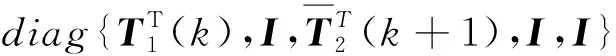
(26)
式(26)满足的充分条件是式(19)和式(27)同时成立。
(27)
通过考虑式(6)并利用Schur补引理,式(27)满足的充分必要条件为
(28)
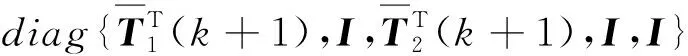
2.4 输入和状态约束条件
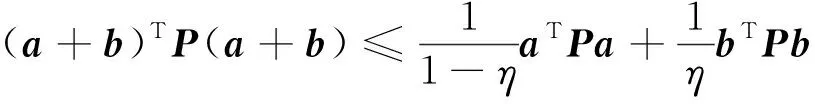
引理2如果式(11)、式(12)、式(13)以及式(17)~式(20)满足,并且式(29)和式(30)成立,则式(2)中输入和状态约束得到保证。
(29)
(30)
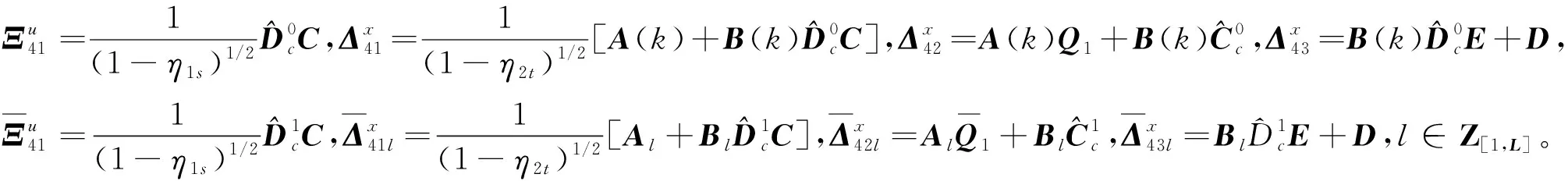
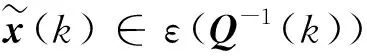
(31)
利用Schur补引理,式(31)等价于如下线性矩阵不等式:
(32)

(33)
通过利用Schur补引理,式(33)等价于:
(34)

为了离线确定标量η1s,s∈Z[1,nu]和η2t,t∈Z[1,nx],采用文献[15]中的类似方法。首先,求解离线优化问题式(35)~(36):
(35)
s.t.式(18)~(19) ,
(36)
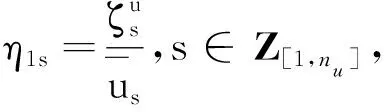
2.5 准最小最大优化动态输出反馈鲁棒MPC算法(无辅助优化)
算法1预先给定标量α1∈(0,1),η1s,s∈Z[1,nu]和η2t,t∈Z[1,nx]。在采样k=0时刻,给定初始估计误差集合ε(Me(0))和控制器状态xc(0)。在每个采样时刻k≥0,执行以下步骤:
(1) 求解如下优化问题:
(37)
s.t.式(11),(12),(13),(17)~(20),(29),(30) 。
(38)
(2) 根据式(20),按照式(39)计算动态输出反馈控制器参数:
(39)
(3) 根据式(3)先计算xc(k+1)和u(k),然后施加控制输入u(k)于式(1)。
文献[11-15]中最小最大鲁棒优化控制考虑到当前和预测的扩展状态约束在共同的鲁棒正不变集合之内,且在预测未来的扩展状态时考虑到当前和未来所有的模型参数以及干扰的不确定性。最小化性能指标上界(即γ(k))的过程和约束当前和未来时刻的扩展状态的鲁棒正不变集合的相关。因此,在优化约束当前以及未来预测的扩展状态的鲁棒正不变集合时,最小最大性能指标中“最大化”会考虑到当前以及未来时刻所有的模型参数以及干扰不确定性。
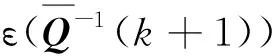
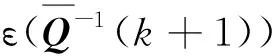
2.6 递归可行性与鲁棒稳定性证明
定理2对于算法1,如果优化问题式(37)~式(38)在k≥0时刻可行,则其递归可行性满足。当系统式(6)收敛到平衡点附近时,系统式(1)稳定在平衡点附近的有界区域内,并且式(2)中输入和状态约束在k≥0时刻总是满足。
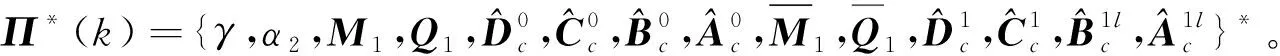
(40)
(41)
(42)
在k+1时刻,通过进一步令
则优化问题式(37)~式(38)中约束在k+1时可满足。因此,在k时刻优化问题式(37)~式(38)的最优解能够构造其在k+1时刻的可行解,从而使得算法1中优化问题式(37)~式(38)的递归可行性得到保证。
为了证明被控系统的鲁棒稳定性,考虑如下标称扩展闭环系统 (即系统式(6)不存在有界干扰):
(43)
(44)
约束式(17)和式(18)分别确保式(24)和式(28)满足。根据Schur补引理和考虑标量α1∈(0,1),式(24)和式(28)分别保证式(45)和式(46)成立:
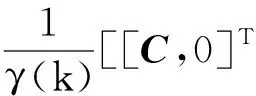
(45)
(46)
上述式(45)和式(46)分别保证条件式(47)和式(48)成立。
(47)
(48)
通过对式(48)从i=1到i=∞进行加和,并且综合式(47),可得到代价函数J∞(k)的上界如下:
(49)
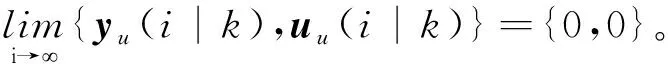
3 相关输出反馈鲁棒MPC算法对比
3.1 准最小最大优化动态输出反馈鲁棒MPC算法(带辅助优化)
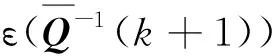
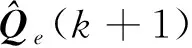
(50)
(51)
(52)
(53)
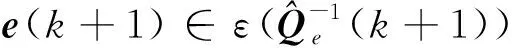
(54)
此外,约束eT(k)Me(k)e(k)≤1和wT(k)Pww(k)≤1可分别表示为式和式(56)中不等式。
ξ(k)Tdiag{1,-Me(k),0}ξ(k)≥0 ,
(55)
ξ(k)Tdiag{1,0,-Pw}ξ(k)≥0 。
(56)
通过利用S-procedure,知“式(55)和式(56)⟹式(54)”成立的充分条件为存在非负标量β1和β2使得下式成立:
β2ξ(k)T(k)diag{1,0,-Pw}ξ(k)≥0 。
(57)
式(57)的充分必要条件为
(58)
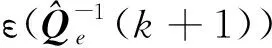
算法2在k=0时刻,标量α1∈(0,1),η1s,s∈Z[1,nu],η2t,t∈Z[1,nx],初始估计误差集合ε(Me(0))和xc(0)的选取同算法1。在每个k≥0时刻,执行以下步骤:
(1) 执行算法1中的步骤(1)~步骤(4)。
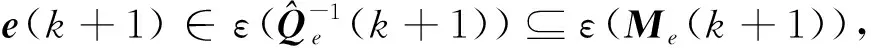
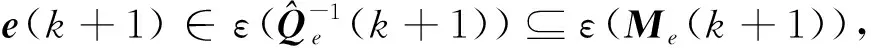
3.2 文献[15]中输出反馈鲁棒MPC算法对比
文献[15]中的算法4所提出的动态输出反馈鲁棒MPC的主优化问题虽然采用多步闭环系统状态预测,并且预测的扩展状态在不同的鲁棒正不变集合之内,但是未考虑当前采样时刻的精确已知模型参数,因此造成了主优化问题保守性。此外,文献[15]中算法4的主优化问题中当前和未来时刻的动态输出反馈控制器参数采用了参数依赖形式,并且考虑到干扰以及量测相关的矩阵为多胞不确定性形式,因此引入大量的双凸组合形式约束,从而造成主优化问题在线计算量随着闭环预测时域的增加而显著地增加。在辅助优化更新估计误差集合方面,文献[15]中的“辅助优化问题式(77)~式(79)”同样可以实现通过误差系统进行估计误差集合计算以及与扩展状态不变性得到的估计误差集合进行比较。然而文献[15]中“辅助优化问题式(77)~式(79)”所涉及到多参数选取以及多约束存在情况,往往造成辅助优化难以可行及计算量大的问题。因此文献[15]中“辅助优化问题式(77)~式(79)”可以改进为引理3中的优化问题式(50)~式(52)。为体现文中算法1的优势,针对算法3进行对比,其综合文献[15]中算法4的“主优化问题(73)”以及文中辅助优化式(50)~式(52)。
算法3在k=0时,标量α1∈(0,1),η1s,s∈Z[1,nu],η2t,t∈Z[1,nx],集合ε(Me(0)),以及xc(0)选取同算法 1。设定闭环系统预测时域nc,并且固定U(k)=I。在每个k≥0时刻,算法步骤如下:
(1) 求解文献[15]中算法4的“主优化问题(73)”并计算矩阵Me(k+1)。
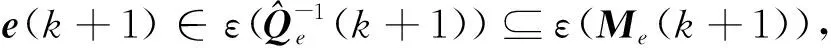
在算法1中,主优化问题式(37)~式(38)中考虑到了当前时刻模型参数精确已知情况,并且考虑到当前和未来时刻预测闭环系统状态在不同的鲁棒正不变集合之内,因此算法1中利用预测的扩展状态不变性可以得到下一时刻精确的估计误差集合的界,并且不需要更进一步地通过辅助优化式(50)~式(52)。在算法2中,虽然在步骤(2)中考虑了辅助优化式(50)~式(52),但考虑到预先计算的ε(Me(k+1))保守性已经显著降低,则辅助优化式(50)~式(52)往往难以可行,因此失去了辅助优化进一步降低估计误差集合保守性的意义。在算法3中,虽然文献[15]中算法4的“主优化问题式(73)”考虑了多步闭环预测模型预测控制优化,但是当前时刻精确已知模型参数未在主优化问题中考虑,从而造成计算的估计误差集合ε(Me(k+1))的保守性。虽然算法3中辅助优化式(50)~式(52)更容易可行,但未必能显著降低估计误差集合更新保守性和提升系统控制性能。
4 仿真算例
选取文献[15]中仿真算例,其中针对系统式(1)的模型参数为
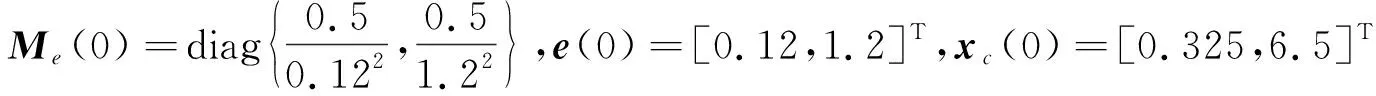
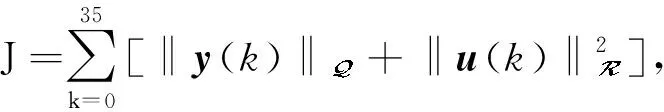
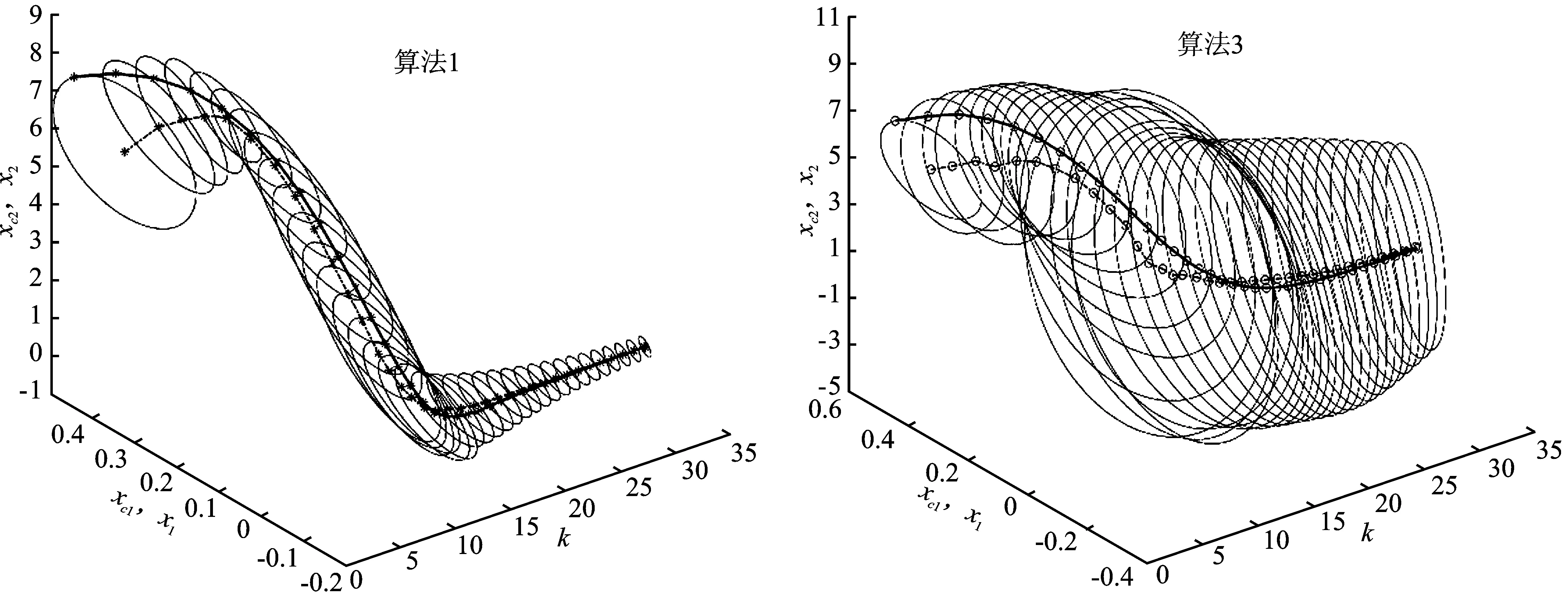
图1 控制器状态、真实状态以及估计误差集合响应图(椭圆中心带符号虚线:控制器状态;带符号实线:真实状态;椭圆:估计误差集合)
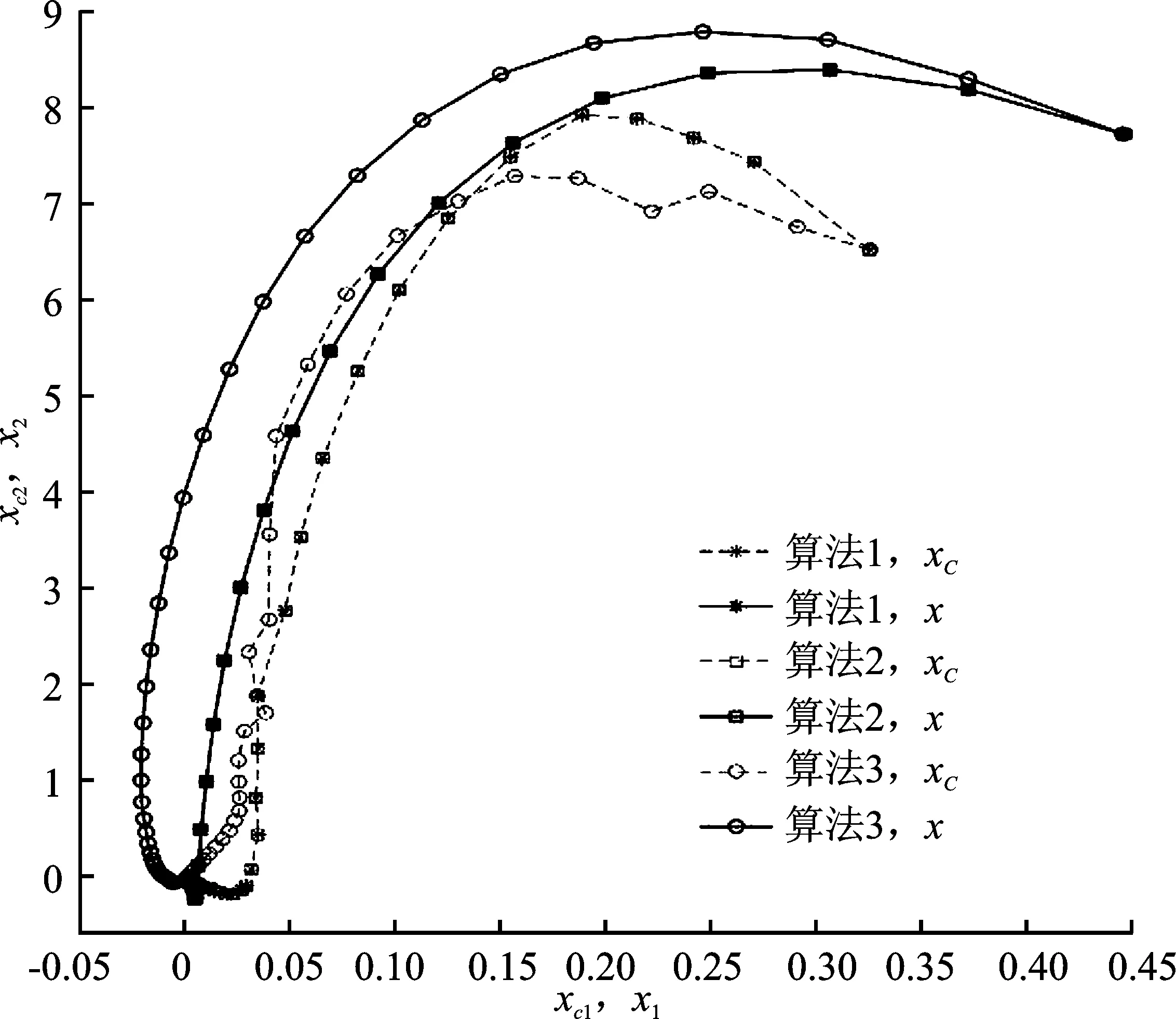
图2 不同算法的闭环系统轨迹图比较

图3 不同算法的控制输入比较
5 结束语
通过构建准最小最大优化形式的鲁棒优化问题,针对包含有模型参数和干扰不确定性系统的动态输出反馈鲁棒MPC进行了研究。通过借鉴鲁棒正不变集合理论和线性矩阵不等式技术,将当前和预测的闭环系统状态分别约束在不同的鲁棒正不变集合内,并且考虑当前时刻精确已知模型参数,从而降低了动态输出反馈控制器保守性。通过考虑预测闭环系统在鲁棒正不变集合的不变性进行估计误差集合更新,从而避免了辅助优化问题求解。当闭环系统收敛到平衡点附近时,则被控系统稳定在平衡点附近的有界范围内。所设计的算法不仅提升了控制性能和确保递归可行性,而且降低了在线计算量。

