基于细节关注的高光谱与多光谱图像融合算法

方帅， 闫明畅， 张晶， 曹洋

1. 合肥工业大学 计算机与信息学院, 合肥 230601;

2. 工业安全与应急技术安徽省重点实验室, 合肥 230000;

3. 中国科学技术大学 自动化系, 合肥 230027

1 引 言

高光谱图像HSI（Hyperspectral Image）与多光谱图像MSI（Multispectral Image）是在遥感领域广泛使用的两种图像，它们在环境监测、目标检测、矿产勘探等应用中发挥着重要作用（Lorente 等，2012；张兵，2016；Yokoya 等，2017；徐冠华 等，2016）。HSI 包含大量的光谱信息，为了保证足够高的信噪比，通常在更大的空间区域中进行光子收集。因此，与MSI 相比，HSI 空间分辨率要低得多。这种低空间分辨率极大影响了HSI 的实用性。因此，把低空间分辨率的HIS，即LR-HSI（Lowresolution HSI）与同一场景下的高空间分辨率的HR-MSI（High-resolution MSI）融合以获得高空间分辨率的高光谱图像HR-HSI（High-resolution HSI）是解决此类问题的一种方法（Dian 等，2017）。

早期LR-HSI 和HR-MSI 融合方法是从Pansharpening（Alparone 等，2007）发展而来，而全色图像不包含光谱信息，这类方法的融合结果存在较大光谱畸变；接着贝叶斯框架下的融合算法（Hardie 等，2004；Wei 等，2014）被提出，此方法引入先验知识降低问题复杂度，再通过最大后验概率实现对问题的求解；另外，假设HSI的光谱像素存在于低维子空间，并通过提取图像光谱特征和求解系数来重建HR-HSI的一系列低维模型方法被提出。近年来，由于深度卷积神经网络在图像特征表示的突出表现，基于深度学习的解决融合问题的算法（Palsson 等，2017；Yang 等，2018）被提出。

以上介绍中，基于低维子空间的融合方法得到广泛的研究（李树涛 等，2021），又可细分为基于解混的方法、基于字典学习的方法和基于张量分解的方法。基于解混的方法利用端元矩阵与丰度矩阵的乘积表示HR-HSI（张兵，2016）；Yokoya 等（2012）提出了耦合非负矩阵分解CNMF（Coupled Nonnegative Matrix Factorization）融合方法，但由于非负矩阵分解的代价函数是非凸的，所以导致融合结果不稳定；Lin 等（2018）和Simões 等（2015）在此类融合框架下增加正则项，将非凸问题转化为凸问题求解，解决了求解结果不稳定的缺点。但是，解混得到的初始化端元矩阵对融合结果的稳定性依然有影响。为了避免端元变异性对局部区域的影响进而导致融合结果不稳定的情况，Wu 等（2020）提出了低秩矩阵估计算法，在全局和局部的低秩光谱—空间数据结构中，建立了算法解决方案，但是该方法没有充分利用HRHSI的先验信息。

基于字典学习（Dong 等，2011；Li 等，2014）的融合方法利用光谱字典与稀疏的系数矩阵的乘积表示HR-HSI。NSSR（Non-Negative Structured Sparse Representation）（Dong 等，2016）提出了基于聚类的非负结构稀疏表示框架，该框架利用空间相关性和谱相关性，将估计得到的系数矩阵与光谱字典结合起来重建高光谱图像；SSCSR（Self-similarity Constrained Sparse Representation）（Han 等，2018）基于HR-MSI的全局结构自相似性与局部光谱自相似性，提出了稀疏表示的相似性约束；LRSR（Lowrank Sparse Representations）（Dian 等，2018）提出空间意义上的局部低秩约束。以上这3种算法是较为典型的基于字典学习的融合算法，主要利用先验信息设计正则项，对系数估计进行改进。由于遥感图像邻近效应作用，尤其图像边缘部分多种目标混杂导致光谱信息非常复杂，现有构建字典方法忽略了这一问题，进而影响融合结果；其次，在字典确定的情况下，如何更好地重建空间细节，也是需要解决的问题。

基于张量的方法用一个核心张量和3个模方向的字典乘积表示HR-HSI，是基于矩阵分解的提高版。由于3D 张量与高光谱图像表现形式上的一致性，近年来，张量分解被用于高光谱与多光谱融合（Dian 等，2017和2020；Kanatsoulis 等，2018）。Dian 等（2017）首先提出非局部空间自相似性稀疏张量分解的融合算法，针对各簇相似块分别学习3个模态的字典，并通过对所学习的字典进行稀疏编码来估算核心张量，从而实现HR-HSI 的重建。此方法产生了良好的融合结果，但有很多问题需要考虑，比如将2D 空间信息割裂为x模态和y模态分别表示是否合适、利用高斯核进行字典下采样是否合适等。基于张量分解融合算法作为一类新的方法，为解决此类问题提供了新思路。

从算法的融合效果上分析，现有算法的空间与光谱重建误差都主要体现在图像的边缘和细节区域（孟祥超 等，2020；Dong 等，2016）。在空间特性上，纹理、轮廓、边缘等细节区域不够准确；在光谱特性上，图像平坦区域光谱特性较为稳定，而细节区域由于图像的邻近效应，其光谱表现为复杂性和多样性，现有算法一般难以精确表示。本文提出了基于细节关注的字典构建和图像重建的融合算法，从两个方面给出了相应的解决策略：

第一，提出了分层字典学习策略，构建具有更多光谱特征字典集。为了表达LR-HSI 复杂多样的光谱特性，将字典学习分成图像层和细节层。图像层基于光谱相似性对图像进行聚类，具有相似光谱的像素簇共享字典；细节层对图像细节边缘区域学习字典。两层字典组合成光谱字典，为重构图像的光谱特性保持提供了基础和保障。

第二，提出了细节感知误差项和方向自适应全变分EADTV（Edge Adaptive Directional Total Variation）（Zhang 和Wang，2013）约束，从而求解出更加精确的系数，实现高精度图像重建。为了保持重建图像的空间结构和光谱信息，本文更加关注细节感知损失。对于细节边缘区域，利用EADTV 计算最小边缘方向图像梯度，将其转化为对系数的约束，从而实现了对边缘细节的精准表示。

本文算法整体上与基于字典学习的方法框架一致，主要从光谱字典学习和系数估计两方面进行改进，减小了融合图像边缘部分的空间误差和光谱误差。

2 融合算法

融合算法的目标是估计HR-HSI。LR-HSI、HR-MSI 以 及HR-HSI 分 别 用X∈RL×n、Y∈Rl×N和Z∈RL×N表示，其中L和l（L>l）表示图像的波段数，N和n（N>n）表示图像的像素点数目，则X和Y可以表示为Z的线性变换：

式中，矩阵B∈RN×N是点扩散函数，表示Z空间分辨率中高光谱传感器的点扩展函数，M∈RN×n是一个下采样矩阵，R∈Rl×L表示Z映射到Y的光谱响应函数。对于给定的X和Y，可以最小化以下误差来估计Z：

式 中，E∈RL×K是 光 谱 字 典，A=[a1，a2，…，aN]∈RK×N是对应的稀疏系数矩阵。再考虑低秩性，式（3）可以写为

本文的目标是求解更加精确的光谱字典E和系数矩阵A，从而获得精确稳定的融合结果。

如图1所示，本文算法主要包括两个模块：字典构造和系数估计模块。字典构建模块进行分层字典学习，包括基于聚类的分类字典学习和基于细节感知的字典学习。基于聚类的分类字典对图像进行聚类，相似的光谱被聚集为一簇且共享一个字典；基于细节层感知的字典，通过细节层感知损失保障字典对于复杂细节区域的表示能力。系数估计的优势主要体现在目标函数的构造，基于细节感知的误差项和方向自适应全变分正则项的构造，保证求解系数矩阵A的精确度，实现高质量HR-HSI重建。

图1 本文算法流程图Fig. 1 Flow chart of the proposed method

2.1 光谱字典学习

本文学习了基于聚类的图像层字典E1和基于分层的细节层字典E2，组合成为光谱字典E=[E1，E2]，即分层字典学习算法，保证字典E具有更强的光谱特征表达能力。首先，建立基于聚类的字典。HSI 具有大量光谱特征相似的地物目标，依据光谱特性采用K-means 对LR-HSI 进行聚类，再针对每类学习光谱字典，保障字典对各类目标都具有可靠的表达能力，如图1图像层所示。下面处理是对每一类分别进行，以第i类为例展示字典学习过程。第i类的目标函数为：

其次，建立细节感知模块来获取细节字典，保障光谱字典在细节区域的表示能力。如图1细节层所示，将HR-MSI 用主成分分析法降维，从前3 个主成分中获取边缘细节并进行膨胀处理，确定细节区域，然后进行下采样映射得到LR-HSI 的边缘细节区域。对细节区域进行字典学习获得光谱字典E2。细节层的目标函数为

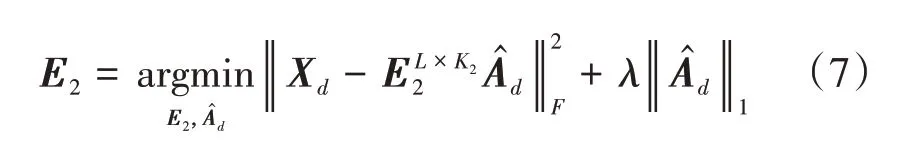
式中，Âd是LR-HSI 细节区域的稀疏系数，K2表示字典原子数。

本文采用与文献（Dong 等，2016）相同的方法进行字典学习，由基于分类的图像层字典和基于边缘关注的细节层字典得到最终的光谱字典E，E的原子数为K。为了验证本文分层字典的有效性，分别建立图像字典和分层字典，并分别用这两种字典重构LR-HSI。图2（a）是图像字典重构的LR-HSI 图像与LR-HSI 原图之间的光谱角映射SAM（Spectral Angle Mapper）；图2（b）是上述分层字典重构LR-HSI 图像与LR-HSI 原图之间的SAM。对比可以发现，分层字典学习算法在光谱信息的保持方面有明显的优势，尤其在边缘区域表现更为突出。字典学习的算法复杂度为O（IJ（K2n+K2+KLn）），I、J为迭代次数。

图2 SAM图Fig. 2 SAM map

2.2 系数矩阵估计

设计系数矩阵估计目标函数时，本文仍然关注细节区域的重构。

首先，提出细节感知误差项。在分层字典学习中，本文提取了HR-MSI细节边缘区域。在设计目标函数时，本文更加关注细节边缘区域的误差，所以将式（5）的第二项改用ω1和ω2控制相对权重的细节边缘区域和非细节边缘区域误差，ω1>ω2。

其次，提出了边缘方向自适应全变分正则项EADTV（Edge Adaptive Directional Total Variation）。为了更加精确描述边缘，构建EADTV约束。EADTV沿边缘方向梯度最小，对细节变化更加敏感。EADTV 在DTV（Bayram 和Kamasak，2012）基础上引入图

像Z的边缘方向参数θ(x，y)，图像Z边缘方向可由以下公式表示：

式中，zx、zy是z(x，y)的梯度向量，此方法对于图像细节边缘部分的保持有显著的效果，在字典E固定的情况下，转换为对系数的约束，TVβ，θ(x，y)(Z)可改写为TVβ，θ(x，y)(A)。

式中，Yd表示图像的细节边缘区域，Y-d是除细节边缘以外的区域。ω1，ω2，α，γ是控制各项相对重要性参数。可以用SALSA 算法（Afonso 等，2011）求解式（11）得到系数A，每次迭代的算法复杂度为O（KNlogN），融合结果Z由光谱字典E与A相乘得到。

3 实验分析

3.1 实验设计

为了验证本文基于细节关注的高光谱与多光谱图像融合算法的有效性，设计以下实验：

（1）为了验证本文细节感知误差项的有效性，在保证字典和其他正则项相同的基础上，对比有无细节感知误差项的目标函数估计系数对融合结果的影响。

（2）为了验证本文分层字典的有效性，分别建立图像字典和分层字典，利用相同的系数求解算法，比较他们的融合结果。

（3）为了验证本文提出的EADTV 正则项的有效性，采用相同的方式获取字典，即基于分层字典学习算法，对比有无EADTV 正则项的目标函数估计系数对融合结果的影响。

（4）为了验证算法的整体有效性，选择5种基于低维子空间的优秀算法与本文算法进行对比，分别是CNMF（Yokoya 等，2012）、Hysure（Hyperspectral Superresolution）（Simões 等，2015）、NSSR（Dong 等，2016）、SSCSR（Han 等，2018）和LRSR（Dian 等，2018）。CNMF 和Hysure 利用顶点成分分析算法VCA（Vertex Component Analysis）获取端元矩阵，其中CNMF用非负矩阵分解以迭代的方式求解端元和丰度矩阵，Hysure 用向量全变分正则项求解HR-HSI 的丰度矩阵。NSSR、SSCSR、LRSR 均使用传统图像字典学习方法获取光谱字典，再分别通过非局部稀疏、全局结构自相似性与局部光谱自相似性、空间局部低秩稀疏来估计系数。

3.2 实验数据与参数设置

本文算法对于同一场景下，且没有发生地物变化的HR-MSI 与LR-HSI 均适用。本文选择两个具有代表性的数据集进行实验：

（1）Pavia University 数据集。Pavia University数据集由反射光学系统成像光谱仪（ROSIS）光学传感器获取。图像大小为610×340，波段数为115，空间分辨率为1.3 m，光谱覆盖范围为0.43—0.86 μm。在去除水蒸气吸收波段后，剩下93 个波段。本文取N=128×128，L=93 大小的数据进行实验，类IKONOS的反射光谱响应滤波器用于生成尺寸为128×128，波段数为4 的HR-MSI，HR-HSI 经点扩散函数下采样四倍获得LR-HSI。

（2）Indian Pines数据集。Indian Pine数据集由AVIRIS 传感器于1992 年在美国印第安纳州拍摄。图像的空间分辨率为20 m，具有224 个光谱波段，光谱覆盖范围在0.4—2.5 μm。本文中取N=120×120，L=224大小的数据进行实验。对应的HR-MSI数据由HR-HSI 根据Landsat-7 传感器的光谱响应函数合成，HR-HSI 经点扩散函数下采样6 倍获得LR-HSI。

本文提出的算法参数选择为ω1=2，ω2=1，α=1.5×10-3，γ=4×10-2，超像素块数T由SLIC 算法得到其中Sw=15，ws=0.5，字典原子数K=52。

3.3 实验结果与分析

为了对各算法融合结果进行评价，本文选取4种评价指标检测融合结果的光谱质量和空间质量，分别是峰值信噪比PSNR（Peak Signal to Noise Ratio）、全局相对误差ERGAS（Relative dimensionless global error in synthesis）（Wald，2000）、SAM 和通用图像质量指数UIQI（Universal Image Quality Index）（Wang和Bovik，2002），以下为实验结果与分析。

细节感知对比：对比有无细节感知误差项对融合结果的影响，从表1中可以看出，对细节关注更多的时候，在Pavia University 数据集和Indian Pine 数据集上，融合结果的各项指标均优于无细节感知误差项的结果，其中反映整体精度的PNSR分别提高了0.0263 和0.0165，反映光谱精度的SAM 分别提高了0.2%和0.016%。同时也证明已有算法在细节处误差较大。

表1 细节感知误差项对比实验结果Table 1 Results for comparison of detail perception error terms

字典对比：对比传统基于图像字典与本文提出的分层字典对融合结果的影响，从表2 可以看出，分层字典学习能有效提升融合结果的质量，在两个数据集上，PSNR分别提高了0.289和0.1924，SAM分别提高了4.6%和2.9%，数据表明在光谱特性的保持方面优势较为突出。

表2 字典对比实验结果Table 2 Results for comparison of dictionary learning

EADTV正则项：在均使用分层字典的情况下，对比在系数估计中有无EADTV 正则项对融合结果的影响。从表3 数据可以看出，两个数据集上PSNR 分别提高了0.4121 和0.3156，SAM 分别提高了4.3%和3.1%，EADTV正则项可以提升融合结果的质量。

表3 EADTV正则项对比实验结果Table 3 Results for comparison of EADTV Regular term

各算法对比实验：图3和图4是Pavia University数据和Indian Pines数据的融合结果及对应MSE图，从局部来看，本文算法在细节边缘区域的误差相对最小，对高光谱图像的细节刻画更加精确；从整体来看，本文算法的误差同样明显小于其他对比算法。

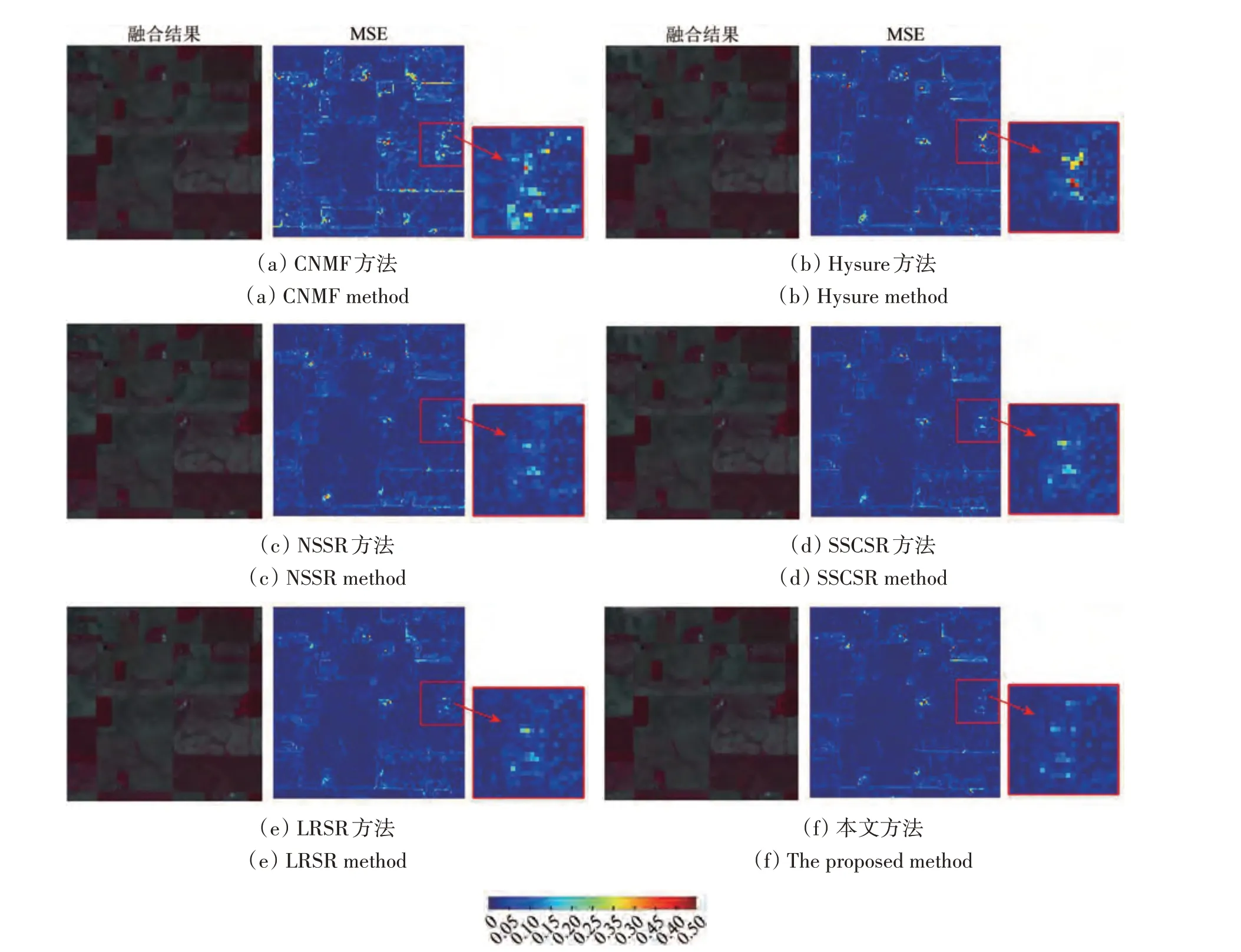
图4 Indian Pine数据融合结果及对应MSE图Fig. 4 Indian Pine data experiment results and corresponding MSE map

表4 和表5 是各算法融合结果在质量评价标准下获得的指标值，本文算法相对于次优解，PSNR值分别提升了0.4945和0.2345，整体精度高，SAM分别提升了6.9%和3.3%。从客观的指标值中不难看出本文算法不仅在空间恢复方面有良好的效果，在光谱保持方面同样优于其他对比算法。本文基于细节关注，实验结果的指标值也能证明细节区域的融合效果的提升能有效提高融合结果的质量。

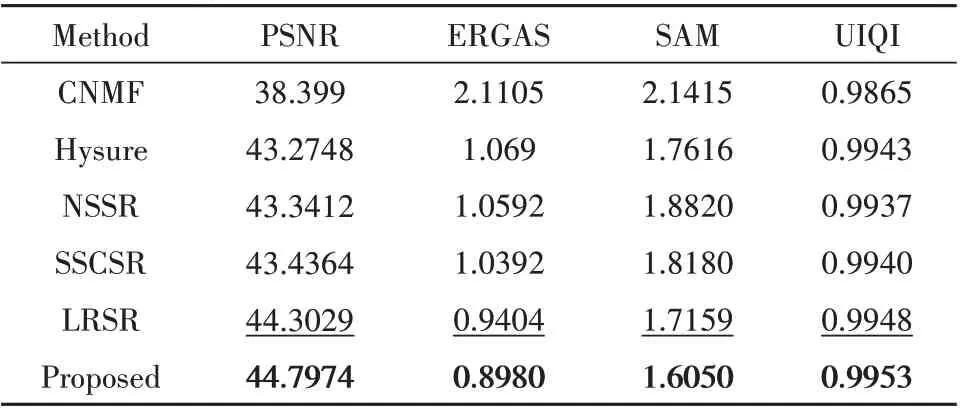
表4 Pavia University数据实验结果Table 4 Results for data set Pavia University

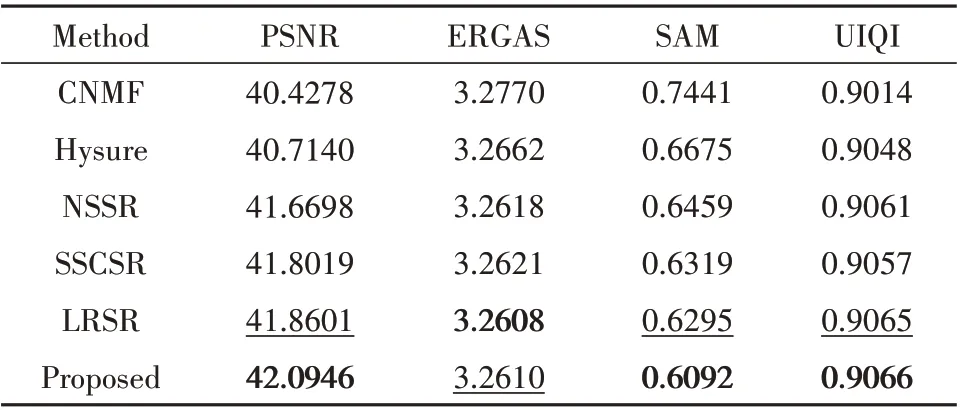
表5 Indian Pine数据实验结果Table 5 Results for data set Indian Pine

4 结 论

通过对现有高光谱与多光谱图像融合算法的分析，本文采用字典学习的方法，提出细节关注的字典构建和图像重建的融合算法。针对现有算法在细节部分重建误差较大的问题，提出了分层字典学习算法，细节感知误差项以及方向自适应全变分正则项，分别对光谱字典求解和系数估计进行改进，减小了融合结果在细节部分的光谱特性和空间纹理的误差，实现了对边缘细节部分的精确表示。消融实验证明细节感知误差、分层字典和EADTV 正则项的引入，在Pavia University 数据集上分别将整体精度（PNSR）提高了0.0263、0.289 和0.4121，光谱（SAM）精度分别提高了0.2%、4.6%和4.3%。在Pavia University 数据集和Indianpine 数据集上的对比实验证明，本文算法相对于次优解，PSNR值分别提升了0.4945 和0.2345。实验印证了本文算法在整体上提高了融合结果的精确度，空间和光谱特性上表现出优秀的性能，在视觉效果上了得到了有效提升。