机载LiDAR测深中海底地形坡度的影响及改正

亓超， 宿殿鹏， 阳凡林， 马跃， 王贤昆， 杨安秀，4

1. 山东科技大学 测绘与空间信息学院, 青岛 266590;

2. 自然资源部海洋测绘重点实验室, 青岛 266590;

3. 武汉大学 电子信息学院, 武汉 430072;

4. 自然资源部第二海洋研究所, 杭州 310012

1 引 言

水深测量是沿岸复杂海域海洋测绘的首要任务，是航海、海岸带管理、海洋环境以及海洋工程等领域的关键参数（吴自银 等，2017；赵建虎等，2017）。目前，水深数据通常使用船载多波束测深仪MBES （Multi-beam Echo Sounder）和单波束测深仪SBES （Single-beam Echo Sounder）等声学方式采集获得（阳凡林 等，2008；Theberge，2013；刘永明 等，2017；赵建虎 等，2017），该方式可在深水区域实现水深的高效测量。然而由于海岸带、海岛礁等周边区域陆海相互作用明显、地形变化剧烈，船载声学测量方式存在通航受限的问题，测量难度相对较大、测量效率相对较低（李清泉 等，2017；宿殿鹏，2018）。全波形机载LiDAR 测深ALB （Airborne LiDAR Bathymetry）的出现解决了上述问题。ALB 是近几十年发展起来的一种主动、非接触式海洋测深技术，在浅于50 m的沿岸水域，其具有测量精度高、覆盖面广、周期短以及高机动性等优点，可以弥补近岸水深数据的测量空白，能够有效实现海陆过渡带地形的无缝拼接（Guenther，2007；马洪超和李奇，2009；Doneus 等，2013；李凯 等，2015；黄荣永 等，2019；刘嘉鎏 等，2020；李玉美 等，2021；唐军武 等，2021）。ALB 技术利用具有较强透水能力的绿色激光（532 nm）进行探测，从发射时起，绿色激光脉冲便会与周围环境产生相互作用，直到脉冲从海底反射回去并被ALB接收器接收（Philpot，2019；宿殿鹏，2018）。整个过程ALB 系统通过接收器接收记录返回激光脉冲的能量强度随时间的变化（即波形），继而采用相应的波形分解方法对波形数据进行分解，提取海面和海底反射回波，以进一步得到每一束激光光束到达海面和海底之间的旅行时间差，再综合考虑ALB 系统标定参数、扫描天底角、实时位置和姿态信息，即可计算出激光点在海底的几何位置信息（Guenther，2007；翟国君 等，2014；李洪鹏 等，2019；Philpot，2019）。

目前，国内外学者相关研究已经证明，ALB测深系统接收波形受系统与环境因素的共同影响，其中系统因素包括激光发射天底角、接收视场角FOV （Field of View）以及激光发射脉冲等，环境因素包括海面波浪起伏、海水水质、水深、海底底质类型以及海底地形起伏等（宿殿鹏，2018；Maas 等，2019；Su 等，2020）。通常情况下，对于给定ALB 系统，系统因素是固定不变的，但环境因素会随时间、空间发生变化，其在ALB 测深误差中占主导地位。Jutzi 和Stilla（2006）已经证明陆地机载LiDAR 系统所接收的地面反射波形特征会受地形坡度变化的影响而产生一定的测量误差。然而，关于海底地形坡度对ALB 系统接收的海底反射波形的影响知之甚少（Wang 和Philpot，2002；Tuell 和Park，2004；Tuell 等，2005；Peeri等，2011）。小脚印ALB 系统激光脉冲通过激光器以一定发散角（1—5 mrad）向下发射，其到达海面时并不是一个点，而是形成一定范围的类圆形光斑，当其穿透水体到达海底的过程中，由于水体散射的影响，在海底将形成更大范围的光斑（相对于海面）（Guenther，2007；Peeri等，2011）。假设ALB 激光光斑内海底地形是平坦的，则海底反射回波可用平坦海底目标剖面的概率密度函数与目标响应的卷积来描述（Su 等，2020）。当海底是平坦的（图1（a）），其概率密度函数可以认为是高斯分布；然而，实际上海底不可能是绝对平坦的，往往存在地形坡度变化，将导致光斑范围内产生水深差异和一定的坡度（图1（b））。与入射在平坦海底上的激光束相比，具有坡度的海底地形反射产生的ALB 海底反射回波将出现波形展宽和峰值位置偏移等现象，难以准确判断海底反射回波的波峰位置，进而导致机载LiDAR 水深测量值不准确的问题（Philpot，2019）。

图1 海底地形坡度对海底反射回波的影响Fig. 1 Effect of seafloor topography slope on seafloor contribution

Wang 和Philpot （2002） 通 过 分 析SHOALS-400 ALB 系统所采集的倾斜沙质（水深4.4 m）海底ALB 数据，也发现了图1 中的现象。当ALB 测深作业时，飞机航线沿南北方向，海底反射回波的峰值位置在每个相同的飞行航线内以及沿相同方向的飞行航线之间几乎保持一致；但在相反方向的航线之间所获得的海底反射回波的峰值位置存在显著差异。Steinvall和Koppari（1996）等通过仿真模拟不同海底地形斜率和激光入射角的海底反射回波，以研究ALB 系统测深的准确性，结果表明，当海底地形坡度在0—15°时，海底反射回波的振幅值发生了明显变化，同时测量深度的变化为3%；Bouhdaoui等（2014）的研究也证明了图1 中所述问题，但他们只是将激光光斑内水深信息在二维空间中进行了描述，假设光斑内地形是一条具有深度信息的线，忽略了光斑内海底地形的三维空间信息，且未考虑光束直径与水深的关系；Abdallah 等（2012）所提出的Wa-LiD 波形仿真模型能够根据ALB 系统相应的系统参数以及环境参数对ALB 反射波形进行较好的仿真模拟，但Wa-LiD 波形仿真模型未考虑海底地形的连续性，若简单地用其进行波形仿真，所得到的是某一点的海底反射回波，往往会忽略ALB 激光光斑内的海底地形坡度对反射回波的影响，进而限制对真实波形的有效仿真表达。

针对上述问题，本文在综合分析考虑ALB 系统机理以及海底地形坡度对海底反射回波影响的基础之上，提出了一种机载LiDAR 测深的海底地形坡度影响改正方法。该方法在限制ALB 其他误差源干扰的同时，假设到达海底的激光脉冲能量在激光波束立体角（光束剖面）内呈高斯空间分布，进而着重分析阐明ALB 激光光斑范围内不同海底地形坡度对海底反射回波波形的影响规律，并构建ALB 测深误差方程以对测深误差进行修正，进一步提升小脚印机载LiDAR 测深精度，以满足IHO标准要求（IHO，2020）。

2 机载LiDAR 测深中海底地形坡度的影响

由于扩散作用，激光脉冲在水体中被扩展为圆锥形，当其到达海底后照射形成一定范围的光斑。海底地形坡度将造成光斑内海底空间垂直深度的变化，继而产生海底反射回波的展宽、峰值位置偏移等现象（Philpot，2019）。为准确描述ALB 激光光斑内连续海底地形反射而成的海底反射回波，本文通过ALB 激光光斑内局部地形参数模型FTPM （Footprint-scale Topography Parameters Model）将海底地形与坡度、水深等海底三维信息联系起来，以实现ALB 海底反射回波模型的构建，进而分析得到海底地形对ALB测深的影响规律。

2.1 局部地形参数模型

本文构建FTPM 的目的在于通过构建ALB激光光斑内的水深值与海底坡度之间的关系，以准确描述海底地形的变化。如图2所示，当ALB激光脉冲发射到达海面和海底时，分别形成了以Rw和Rb为半径的圆形光斑。如图2（a）所示，该模型将圆心为P0、半径为Rb的圆形海底激光光斑以一定夹角α平均分为n部分（n=360°/α），其中，每一部分用P0Pi（i=1，…，n）表示，其端点Pi的水深为Di。

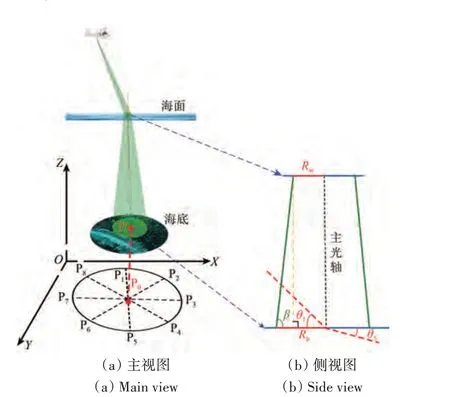
图2 局部地形参数模型示意图Fig. 2 Schematic diagram of footprint-scale topography parameters model

利用几何关系及正弦定理，即可计算得到P0Pi的长度Li，如式（1）和式（2）所示。其中，Li的长度与激光光斑半径Rb和θi有关，当海底平坦时（即P0Pi与水平面的夹角θi为0°），Li等于Rb。

式中，Li为P0Pi的长度；θi表示P0Pi与真实水深所在水平面的夹角（如图2（b）所示，本文假设当P0Pi在该水深D平面之上，θi大于0；当P0Pi在该平面之下，θi小于0）；D0为光斑中心P0处的水深值。

将计算得到的P0Pi长度Li代入式（3）和式（4）即可分别得到Pi点处的水深Di以及P0Pi段的平均水深-D i。

为更加准确地描述激光光斑内的水深信息，本文根据每一段P0Pi段的长度Li确定相应权重，利用式（5）对所得P0Pi段的平均水深-D i取加权平均，将此加权平均值作为该激光光斑内的平均水深值。

2.2 ALB海底反射回波模型

ALB 系统激光接收器能够以数字化的形式记录每个激光脉冲的全部回波波形信号（Abdallah等，2012；胡善江 等，2019），包括水面反射回波、水体散射回波、水底反射回波以及噪声四部分。基于2.1 节所构建的FTPM 实现ALB 海底反射回波模型的构建，将ALB 激光光斑内的海底地形坡度、水深等海底三维信息与海底反射回波具体联系起来。

2.2.1 基于海底地形坡度等距离散化的回波模型

为便于对ALB 激光光斑内连续海底地形进行解释，还原激光光斑内真实地形所反射形成的海底反射回波，本文提出了一种基于海底地形坡度等距离散化的回波模型。首先将光斑内FTPM 的每一段P0Pi表示为若干具有不同水深、相同坡度的光滑表面，然后通过计算若干表面反射回波的积分和的平均值作为P0Pi段的反射回波，最后以P0Pi长度Li作为权重，取激光光斑内n段P0Pi的反射回波的加权平均值作为海底反射回波的初始结果。

为避免离散化地形对波形仿真造成混叠干扰，基于Nyquist-Shanon 采样定理，等距离散化最小采样间隔Δx须小于ALB 采样时间间隔与光速乘积的一半（Bouhdaoui等，2014），即：

式中，cw为激光在水中的传播速度；Tg表示机载LiDAR测深系统的采样时间间隔（通常为1 ns）。

为直观地描述海底地形坡度等距离散化模型，绘制了ALB 激光光斑内海底地形的侧视图（图3），该侧视图由P0Pi和P0P（n/2+i）两段组成（i≤n/2）。以Δx为最小采样间隔对P0Pi的长度Li进行等距离散化处理，将其平均分为m部分（x1，x2，…，xj，…，xm），所得的某一部分xj在垂直方向上的水深差Δdj可用式（8）表示，在水平方向上的长度Rtj可用式（9）表示。该方法中m值的确定取决于Δx、Li，且假定Δx内的海底地形坡度恒定。

图3 海底地形坡度等距离散化模型Fig. 3 Equidistant discretization model of the seafloor slope

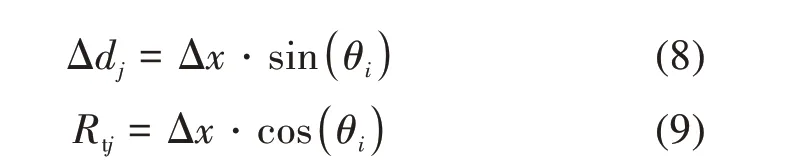
P0Pi段沿X轴的第j部分的水深为Dj（式（10）），利用Wa-LiD模型（Abdallah 等，2012）可得到第j部分所对应的海底反射波形Pbj（t）。

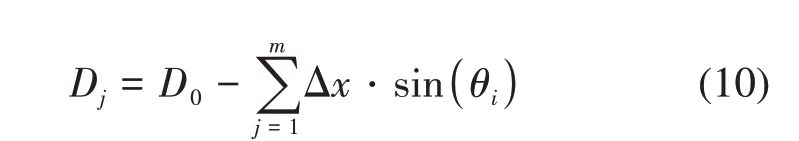
通过计算P0Pi段m个波形Pbj（t）积分之和的平均值即可得到P0Pi段所对应的波形Pbi（t），即：

以每一段P0Pi的长度Li作为权重，计算激光光斑内n个Pbi（t）的加权平均值即可得到ALB 激光光斑内的海底反射回波的初始结果Pb（t），即：

2.2.2 海底反射回波能量校正

在采用Wa-LiD 模型得到ALB 海底反射回波的初始结果Pb（t）之后，还需考虑海底地形坡度对波形的展宽作用（图1）。根据已有研究（Wang 和Philpot，2007）可以校正得到由脉冲展宽效应引起的海底反射回波振幅值损失，校正系数g（ω）为

式中，ω为海底法线与海水中激光光线的夹角，其正负值如图4。

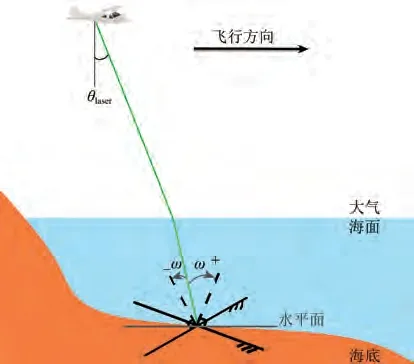
图4 海底法线与海水中激光光线的夹角示意图Fig. 4 Schematic diagram of the angle between the seafloor normal and laser light

图5 表示经g（ω）校正并归一化后的海底反射回波能量随ω的变化关系。当激光脉冲所在方向与海底坡度所在平面垂直时，其回波波宽最小，即处于最压缩状态；当不垂直时，其激光脉冲能量随|ω|的变大而减小。这是因为，ALB 系统所接收的海底反射回波的能量是随时间变化的，其回波波宽随着海底地形坡度的变化而发生展宽现象，即海底反射回波的能量与发射波形相比将会分布在更长的时间内，使得单位时间内的最大返回能量减少。

图5 海底反射回波归一化能量随ω的变化关系Fig. 5 Relationship between the normalized energy of seafloor waveform and ω

因此，通过校正系数g（ω）对海底反射回波能量进行校正后，即可得到顾及ALB 激光光斑内海底地形坡度的海底反射回波，即为

式中，PB（t）为顾及ALB 激光光斑内海底地形坡度的海底反射回波。

2.3 海底地形坡度对ALB测深的影响分析

在分析海底地形坡度对ALB 测深的影响之前，为验证ALB 海底反射回波模型的有效性，分别利用该模型和Wa-LiD 模型（Abdallah 等，2012）对同一激光光斑内相同ALB 参数、相同海底地形变化（海底地形坡度为0°、水深为10 m）的海底回波信号进行构建，如图6所示，第一个回波为海面反射回波，第二个回波为海底反射回波。由于本文未考虑海面起伏等其他因素对波形的影响，两种模型得到的海面反射回波是重合的。另外，两种模型得到的海底反射回波基本一致，但通过Wa-LiD 模型得到的海底反射回波的振幅能量略低于本文模型仿真的波形，这是因为Wa-LiD 模型得到的波形是海底某一深度点所返回的能量；而本文模型得到的海底反射回波考虑了ALB 激光光斑内海底地形的连续性，其回波信号是一定范围内的能量（即该激光的光束中心与其周围能量之和）。

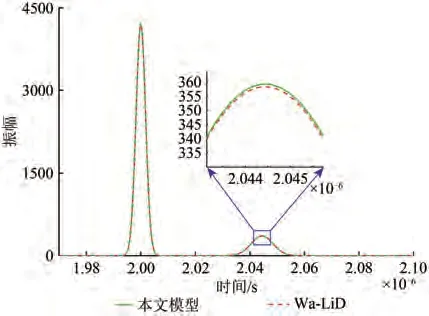
图6 Wa-LiD模型与本文模型的波形比较Fig. 6 Comparison of simulated waveforms between the Wa-LiD model and the developed model

为分析海底地形坡度对ALB 测深的影响，图7（a）绘制了4 组不同海底地形坡度下的ALB海底反射回波。绿色激光脉冲在海水中传播是一个复杂的过程，本文在确定ALB 激光在海底的光斑半径时，采用了前人的经验公式（Guenther，2007；Peeri等，2011）。基于此，分别在平均深度为10 m、光斑半径为1.3 m 情况下，利用本文模型构建了4 种不同海底地形坡度（0°、10°、25°、45°）所形成的ALB 海底反射回波。可以看出，与平坦地形（图7（a）中红色实线）相比，随着坡度的变化，海底反射回波的峰值位置、波宽及振幅能量均存在较为明显的差异，其导致了水深测量误差的产生。为直观地展示上述影响，绘制了不同海底地形坡度与平坦地形（海底坡度为0°）的水深差值，如图7（b）所示，当水深相同时，随着海底地形坡度的增加，水深差值逐渐增加；当海底地形坡度不变时，水深越深，水深差值越大。因此，水深差值可看作为水深和海底地形坡度的函数，并通过该函数关系对误差进行改正，以提升ALB测深精度。

图7 海底地形对ALB测深的影响Fig. 7 Influence of seafloor topography on ALB

3 机载LiDAR 测深的海底地形坡度影响改正方法

3.1 改正方法

机载LiDAR 测深的海底地形坡度影响改正方法的目的为基于本文2.2节海底反射回波PB（t）量化分析海底地形坡度对ALB 测深的影响规律，以进一步提升ALB 测深精度，因此在利用ALB 海底反射回波模型得到PB（t）时未加入噪声的影响；同时，将ALB初始测深值DALB作为激光光斑内的平均水深Dˉ。

利用极大值检测法对ALB 反射回波进行峰值探测求得海面、海底反射回波所对应峰值位置的差异，并结合激光入水折射角即可计算得到相应激光点的水深值（亓超 等，2019）。极大值点位置如式（15）所示。

式中，w为波形数据，diff 为差分运算，sign 为符号函数，find指查找满足条件的数据编号。

通过比较分析一定水深条件下，不同坡度与平坦地形（平均水深所在平面）的海底反射回波，确定相互间的水深差异值ΔD，以构建ΔD与海底地形坡度θ之间的函数关系，即ALB 测深误差方程。通过本文2.3 节分析，本文选用幂律模型（Power Law Model）（Bouhdaoui 等，2014）对该方程进行描述，如式（16）所示：

3.2 实现流程

机载LiDAR 测深的海底地形坡度影响改正方法能够在现有ALB 硬件系统基础之上，仅通过数据处理即可进一步提高ALB 每一束激光测深数据的准确度。该方法的具体实现流程如下（图8）：

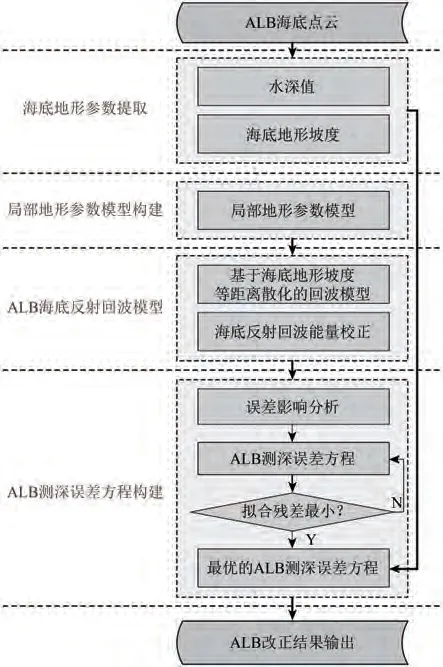
图8 本文方法流程图Fig. 8 Flow chart of the correction method

（1）海底地形参数提取。利用ALB 初始海底测深点云数据提取得到每一激光点所对应的海底三维信息，包括海底地形坡度、水深值。

（2）局部地形参数模型构建。通过将海底激光光斑均分为n部分，构建ALB激光光斑内的不同海底坡度与水深值之间的关系（式6），以此可计算激光光斑内任意位置的水深值，进而实现ALB光斑内海底地形变化的立体描述。

（3）ALB海底反射回波模型。首先基于局部地形参数模型和海底地形坡度等距离散化模型将P0Pi分为m个具有不同水深、相同坡度的光滑表面；然后计算基于Wa-LiD 模型得到的m个表面反射回波积分和的加权平均值，以此作为P0Pi段的反射回波；其次以P0Pi长度Li作为权重，取激光光斑内n段P0Pi的反射回波的加权平均值作为海底反射回波初始结果；最后通过校正系数g（ω）对海底反射回波初始结果的能量进行校正，得到顾及ALB 激光光斑内海底地形坡度的海底反射回波PB（t）。

（4）ALB 测深误差方程构建。通过ALB 海底反射回波模型定量分析不同水深、不同海底坡度对海底反射回波峰值位置变化的影响规律，进而利用参数优化得到最优的ALB测深误差方程。

（5）ALB 改正结果输出。将步骤（1）中提取的海底地形坡度、水深值代入最优的ALB 测深误差方程，并通过式（17）即可得到改正后的ALB测深值DCOR。

4 实验与分析

4.1 实验数据概况

为定量分析评估本文方法的性能，采用2013年1月在中国西沙群岛（图9（a））甘泉岛（图9（b））附近相同海域采集的ALB 和MBES 测深实验数据（宿殿鹏，2018；Su等，2019）。

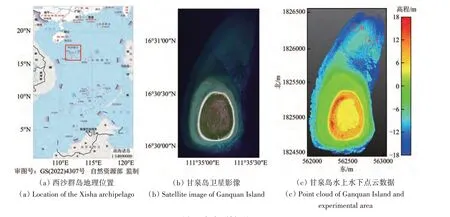
图9 实验区域概况Fig. 9 Overview of the survey area

MBES技术完善，测深精度能够满足IHO S-44特级标准（IHO，2020），而ALB技术相对不成熟，因此，为验证本文方法结果的可靠性，采用MBES数据作为ALB 海底地形坡度误差改正结果的参考数据。实验中，MBES 数据采用R2Sonic 2024 系统采集，其最大量程500 m，量程分辨率为1.25 cm，覆盖宽度10—160°，每发射接收周期（Ping）有256个波束。MBES的测深点密度约为200 points/m2（Wang 等，2021）。

ALB 数据采用Optech Aquarius 机载LiDAR 测深系统进行采集。该系统为直线扫描模式，仅使用532 nm 的绿色激光进行探测，激光脉冲频率为70 kHZ，典型测深能力为1 Secchi 深度。数据采集时，ALB 飞行高度约为300 m，激光器的扫描天底角为15°，激光发散角1 mrad，脉宽8.3 ns，海面风速5 m/s，系统运行3 h，共计获得14 条主测线。利用Optech LMS 软件（Optech Incorporated，2010）对原始ALB 数据进行系统安装偏差校准、多源数据融合、坐标转换以及海气界面折射改正等数据处理，未对本文所讨论海底地形坡度所引起的ALB测深误差进行校正。最终，获得包含1.8×1017个激光点的LAS 数据（图9（c）），海底点密度约为4 points/m2。此外，本文进行波形仿真时所用Optech Aquarius ALB实验时的具体变量如表1所示。

4.2 改正结果

通过ALB 海底反射回波模型利用Optech Aquarius ALB 实验时的具体参数（表1）分析得到48 组数据，如图10 所示，为更加准确、清晰地描述ALB 激光光斑内不同海底坡度所导致的测深误差的变化趋势，将其水深差值的趋势绘制成伪彩色图，可以看出，随着水深和斜率逐渐增加，水深差值越来越大。利用本文改正方法，并基于上述48 组数据，优化得到ALB 测深误差方程的8 个最优参数（表2），将其代入式（16）即可得到最优化ALB测深误差方程。

表1 Optech Aquarius ALB 实验时的具体变量Table 1 Specific variables of Optech Aquarius ALB survey

表2 ALB测深误差方程最优参数Table 2 Optimal parameters of ALB error correction equation

图10 光斑内不同坡度与平坦地形的水深差异Fig. 10 Depth differences caused by seafloor topography at the footprint scale

为便于叙述本文方法的性能，选取两处100 m×100 m 的区块（图9（c）红色框中）数据进行实验验证与分析。如图11所示，区块A、B分别收集了8637 对、8861 对ALB 和MBES 测深数据的同名点对，并分别采用ALB 测深数据提取了区块A、B 的海底地形坡度信息（Yang 等，2020）。将通过ALB测深点云提取的水深和海底地形坡度代入最优化ALB 测深误差方程，并结合式（17）即可完成对ALB 测深误差的改正，改正前后水深较差伪彩色图如图12所示。

综合图11 和图12 可以看出，区块A 水深为4—8 m，区块B 水深为8—15 m，且海底地形坡度变化范围大。如图12（a）和12（c）所示，在应用本文方法改正测深误差之前，两块区块水深差与海底地形坡度（图11（c）和11（f））的空间分布趋势存在明显的关联性，这直接证明了海底地形坡度变化会产生ALB 测深误差；经该方法改正后（图12（b）和12（d）），局部水深差异值得到了一定程度的削弱，使其基本上不再呈现与海底地形坡度相似的空间分布趋势，其中区块A 局部区域的平均水深差异最大值减小至44 cm。这可能与水体散射与水体折射等海洋环境因素导致的测深误差处理模型不完善有关，图12 中水深差异值可能仍存在除海底地形坡度外的其他误差残差；此外，通过图10 发现，海底地形坡度导致的测深误差影响有限，如当水深为20 m、海底地形坡度为40°时，水深较差改正值也未超过20 cm。因此，可认为该方法较好的改善了海底地形坡度导致的测深误差。

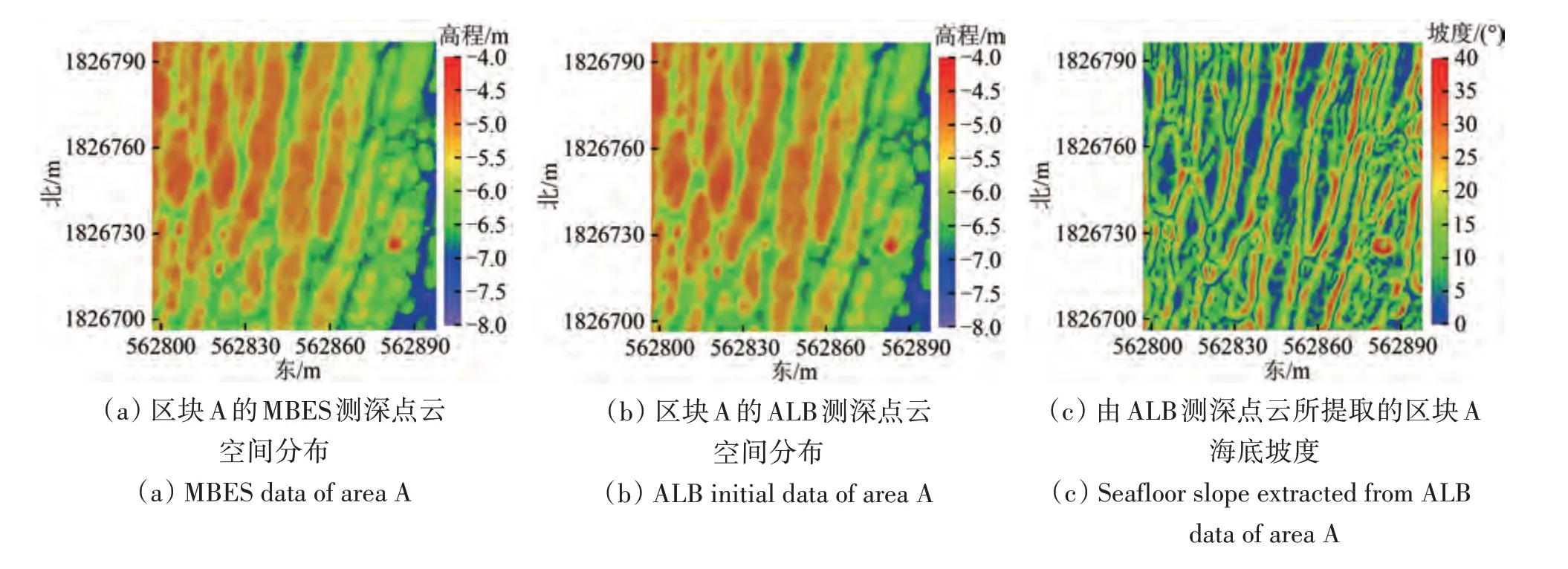
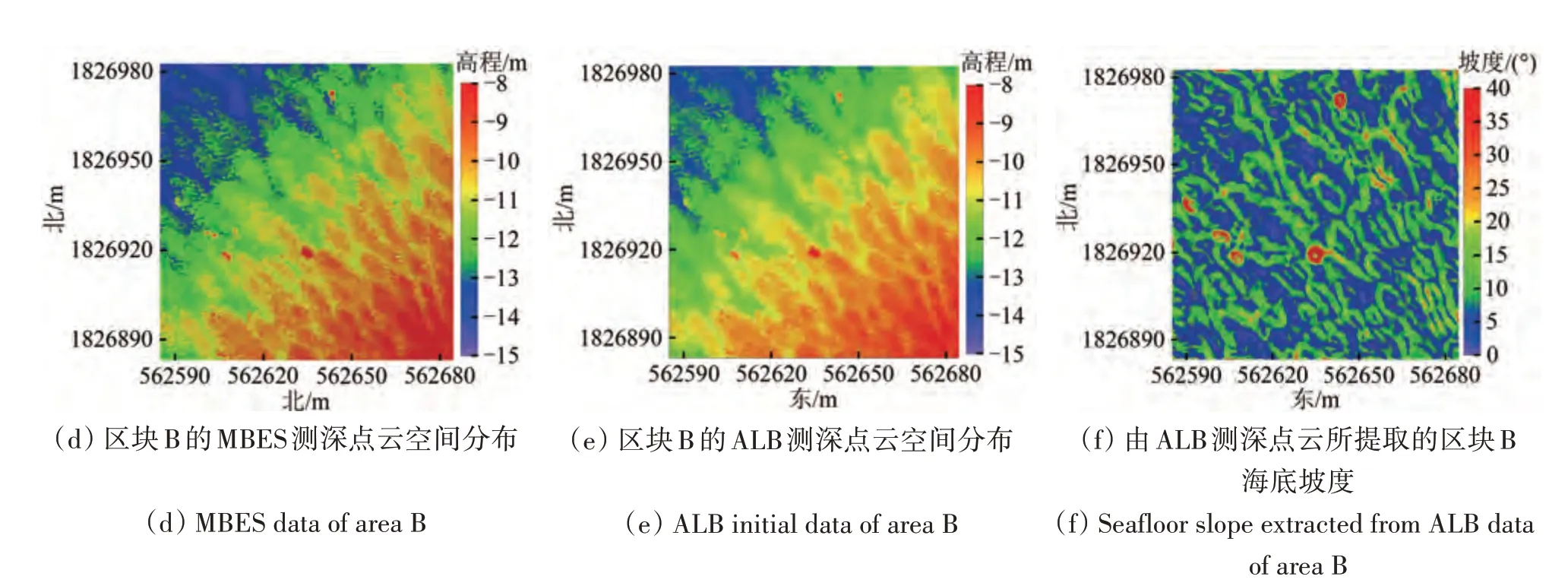
图11 MBES和ALB测深点云数据以及所提坡度信息Fig. 11 Point cloud （MBES and ALB） and seafloor slope in the areas of interest

图12 ALB误差修正前后与MBES水深差的空间分布Fig. 12 Spatial distribution depth differences between MBES and ALB before and after error correction in the areas of interest

4.3 性能分析

为定量分析本文方法对测深误差的改正性能，如图13 所示，将该区块A 和B 改正前后的水深较差按照水深分布绘制散点图，计算并绘制其限差（中误差RMSE（Root Mean Square Error）的2 倍），同时利用IHO S-44 所定义的测深总垂直不确定度TVU（Total Vertical Uncertainty）1a 级标准进行判断（图13红实线），其规定的最大允许值T（95%置信水平），如式（18）所示。（IHO，2020）。

图13 ALB和MBES误差修正前后水深差散点图Fig. 13 Scatter plot of depth differences between MBES and ALB before and after error correction in the areas of interest

根据图12 和图13 可以看出，运用本文方法可较好地修正局部水深差异，使其几乎全部达到了IHO S-44 1a 级标准要求。在改正前，平均绝对误差MAE（Mean Absolute Error）为14.6 cm，RMSE为18.5 cm；经改正后，MAE 和RMSE 分别减小到9.4 cm和12.3 cm，即分别降低了35.6%和33.5%。

为充分验证本文方法的有效性，选择利用区块A 做进一步分析。通过区块A 更为精确的MBES点云（图11（a））分别提取水深和海底地形坡度等海底三维信息代入优化后的ALB 测深误差方程，以得到修正后的ALB测深值，并与MBES测深数据比较，结果表明：基于MBES 点云数据所得MAE和RMSE 分别为6.9 cm 和8.7 cm；基于ALB 点云数据所得MAE和RMSE分别为6.5 cm和8.3 cm。上述误差修正结果几乎相近，这也证明了本文所提方法的有效性。

5 结 论

本文提出了一种机载LiDAR 测深的海底地形坡度影响改正方法，通过考虑ALB 激光光斑内海底地形的连续性，针对性地解决了海底地形坡度变化导致每一束ALB 激光脉冲的测深不确定性问题，为进一步提升小脚印ALB测深精度提供了一种新的解决方案。将本方法应用到中国南海甘泉岛附近海域采集的Optech Aquarius ALB 数据处理中，并使用R2Sonic 2024 MBES 数据作为改正结果的参考数据。实验结果表明，经过该方法对ALB 测深数据进行改正后，MAE和RMSE分别降低了5.2 cm和6.2 cm，即分别降低了35.6%和33.5%。该方法具有良好的可行性，可有效削弱海底地形坡度引起的测深误差，并能够使得ALB 测深数据满足IHO S-44 1a 级标准要求。因此，通过本文方法能够在无需对ALB 系统硬件进行升级改进的条件下，仅通过数据后处理，即可进一步提高ALB 测量精度，具有有益的借鉴意义与应用价值。