复杂环境软土地层盾构隧道推进实时动态仿真及变形预测研究
——以苏州地铁S1号线盾构区间为例
邓声君, 何 杨, 陈浩林, 周 峰, *, 朱 锐, 师文豪, 王 源, 马千里
(1. 南京工业大学地下工程系, 江苏 南京 211816; 2. 浙江大学滨海和城市岩土工程研究中心, 浙江 杭州 310058; 3. 苏州科技大学土木工程学院, 江苏 苏州 215011; 4. 北京建工集团有限责任公司, 北京 100032)
0 引言
随着城市轨道交通的快速发展,我国隧道及地下工程建设日益增多,盾构法作为一种隧道暗挖施工方法,因其安全可靠、对地面及周边环境影响小的优势,在以软土地层为主的城市隧道建设中被广泛采用,而盾构施工对周边环境的影响是目前普遍关注的热点问题[1]。
盾构施工对地层变形影响的研究主要分为经验分析法、理论解析法、数值模拟法等。经验分析法以经典的Peck公式为代表[2],由于实际工程的特殊性与复杂性,Peck公式往往过于依赖经验简化,国内外学者结合实测,在此基础上进行了修正[3-6]。刘波等[7]基于叠加原理,推导了双洞平行隧道开挖引起的地表横向沉降计算公式; 师刚等[8]与秦睿成[9]均基于实测数据和经典公式进行拟合,得到了双线并行的沉降量分布函数; 张运强等[10]通过引入不同的土体参数,对已有沉降公式的参数进行调整,得到了更精确的针对不同土体参数的取值。理论分析法也是一种重要的研究手段,刘纪峰等[11]基于均质半无限空间假定和弹塑性力学原理提出了一层适合浅埋隧道地表沉降预测的弹塑性解; 刘波等[12]通过引入随机介质理论,建立了考虑隧道不均匀收敛变形的地表沉降预测模型; 邵珠山等[13]以随机介质理论为基础,提出了不同断面类型下隧道变形和地表沉降的计算模型。由于理论计算的基本假定与实际工况有差距,计算结果与实测存在误差,而数值模拟法可以综合考虑施工过程和土层的复杂性,其计算结果具有直观性和良好的精确性等优势,在实际工程中应用广泛[14-20]。包小华等[21]基于修正剑桥模型,通过有限元软件FLAC 3D对北京地铁14号线双线盾构进行建模,并采用刚度迁移法对盾构掘进及注浆过程进行模拟,分析了注浆等因素对地表沉降造成的影响; 潘涛[19]以宁波市轨道交通5号线为背景,基于摩尔-库仑模型,通过有限元软件ABAQUS建立了双线盾构隧道及周边单栋建筑的三维模型,重点分析了两线的沉降槽分布规律及对该建筑产生的影响。然而,目前研究大多针对开挖完成后的最终应力状态和变形进行描述,缺乏对开挖过程中土体各应力应变状态及对周边地表环境影响的分析,这不利于实际施工过程中的动态监测与管理。
目前盾构隧道开挖数值模拟研究中常采用摩尔-库仑(Mohr-Coulomb)模型、修正剑桥(modified cam clay)模型、德鲁克-普拉格(Druker Prager)模型及硬化(hardening soil)模型。Atkinson等[22]将应变分为非常小应变、小应变及大应变3类,并发现土体的剪切刚度在小应变区域内存在随着应变的增加而急剧减小的现象。而软土地层的基坑和隧道开挖所产生的应变有很大部分处于小应变区域[23-24]。在此情况下,若忽略小应变特性就会严重低估土体刚度,导致预测变形偏大,使得施工时不得不采用保守措施来满足设计要求,造成不必要的资源浪费,因此研究采用HSS小应变硬化模型。
小应变硬化模型(简称HSS模型)恰能体现土体剪切硬化、压缩硬化及土体小应变特性,能够较真实地反应土体在开挖工况下的变形规律[25-26]。然而,模型中计算参数多,获得对应参数的试验方法相对复杂,且难以确保下穿不同类型建筑物时模拟的准确度。本文基于地层变形和建筑物变形现场实测数据,建立了盾构隧道-周边建筑群一体化实时反馈三维数值模型,通过试验段和预测段模型实时反演得到一套适用性较高的HSS模型计算参数,以实现盾构施工对周边建筑群和地层变形的精细化数值计算。依托下穿多种建筑物的苏州地铁S1号线玉山广场站—珠江路站盾构区间工程实例,验证实时动态反馈模型的适用性,对盾构施工引起的地表及周边建筑物变形规律进行分析,以期为实际施工提供参考。
1 工程概况
苏州市轨道交通S1号线工程起点位于苏州市工业园区,在3号线夷亭路站实现换乘,终点位于昆山市花桥经济开发区,在花桥站与上海11号线换乘。线路全长约41.5 km,途径苏州工业园区、昆山市巴城镇、昆山市高新区、昆山市经济开发区、陆家桥、花桥经济开发区,全线设站28座。本研究工程为玉山广场站—珠江路区间,区间涉及的风险建筑分布如图1所示。
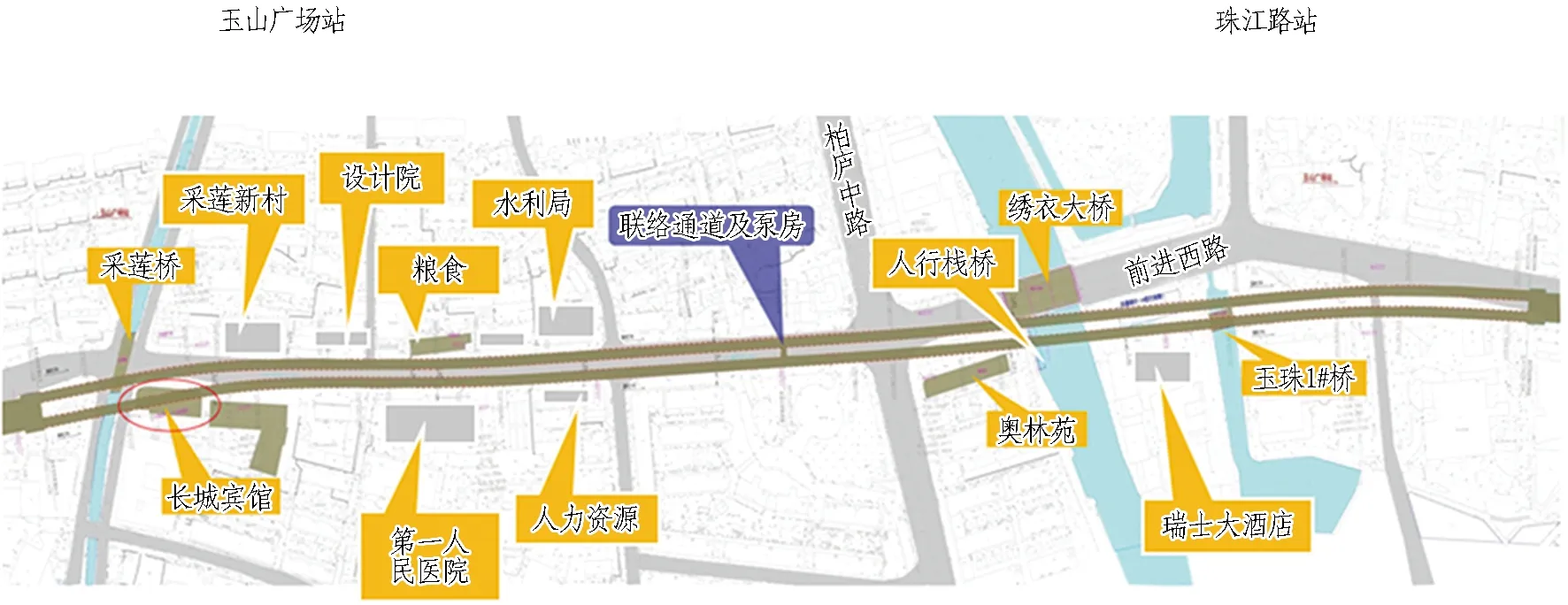
图1 风险建筑分布示意图Fig. 1 Schematic of distribution of risky buildings
玉山广场站—珠江路站区间隧道全长约1 165 m,采用加泥式土压平衡盾构施工,分左右两线依次掘进(先左线掘进、后右线掘进)。其中,区间左线长度为1 168.479 m,区间右线长度为1 165.193 m,左右线总长为2 333.672 m。盾构穿越众多老旧建筑,基础类型涉及各类桩基及浅基础。盾构区域穿越主要地层有②1层粉质黏土、②y层淤泥质粉质黏土、④1层粉质黏土、⑤1层粉质黏土、⑦1层粉质黏土、⑦2层粉土夹粉砂,土层地理力学参数如表1所示。

表1 土层物理力学参数Table 1 Physico-mechanical parameters of soil
盾构顶进过程共穿越11栋中高风险建筑,包含浅基础建筑3栋、桩基础建筑8栋。中高风险建筑基本情况如表2所示。
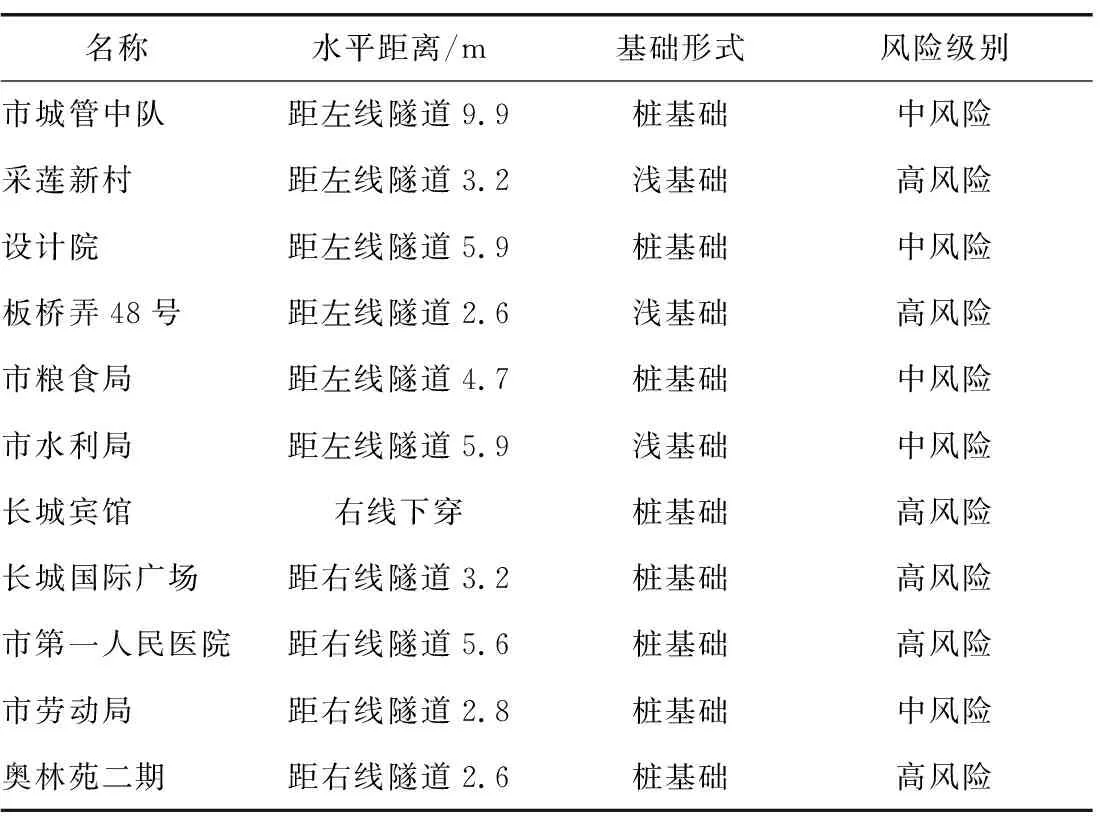
表2 中高风险建筑基本情况Table 2 Basic situation of medium and high risky buildings
2 盾构隧道-周边建筑群全区段一体化施工数值模拟
2.1 有限元计算模型
2.1.1 基本假定与本构模型
采用PLAXIS 3D建立三维数值模型,包含5万个实体单元、9.8万个节点。为简化计算,做如下假定: 不考虑渗流问题的影响; 各土层均质水平分布; 建筑桩基呈矩形均匀排布,建筑荷载转化为面荷载均匀分布于底板,忽略道路荷载及周围堆载; 盾构顶进过程按10 m一环匀速前进。
土体采用HSS本构模型,管片、建筑底板及基础均采用线弹性模型。
2.1.2 模型尺寸及边界条件
模型采用笛卡尔坐标系,隧道轴线方向为y轴,盾构顶进方向为正方向; 与隧道轴线水平垂直的方向为x轴; 与隧道轴线垂直的竖直方向为z轴; 坐标轴符合螺旋定则。
计算范围: 根据建筑风险等级,本模型以高风险建筑长城宾馆西侧86.5 m至高风险建筑奥林苑二期东侧119 m处为边界范围,模型尺寸840 m(长)×140 m(宽)×45 m(厚),土层厚度为45 m。
建筑建模: 通过PKPM建立建筑物上部结构模型,赋予材料属性,以荷载的形式施加于基础上。针对桩基建筑,将基础简化为规律排布的等长桩基,并通过底板结构转化为整体模型,将上部荷载简化为均布荷载施加于底板上,如图2所示。针对浅基础建筑,将其简化为条形基础,同样根据上部结构荷载均匀布荷,如图3所示。

图2 建筑物桩基础模型(市第一人民医院)Fig. 2 Pile foundation model of building (Kunshan first hospital)
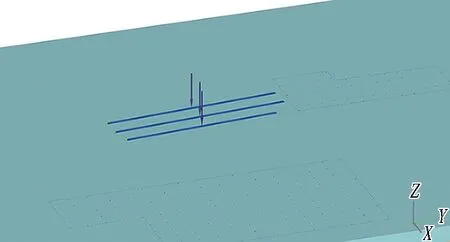
图3 建筑物浅基础模型(板桥弄48号楼)Fig. 3 Shallow foundation model of building (No. 48 Banqiao lane)
隧道位置与尺寸: 隧道分为左右两线,两线中心间距为13 m,埋深为22.38 m,直径为5.9 m,管片材料为C50混凝土,厚度为0.475 m,如图4所示。隧道模型采用线弹性本构,考虑管片接缝的影响,管片刚度折减系数取0.85,其结构材料参数见表3。
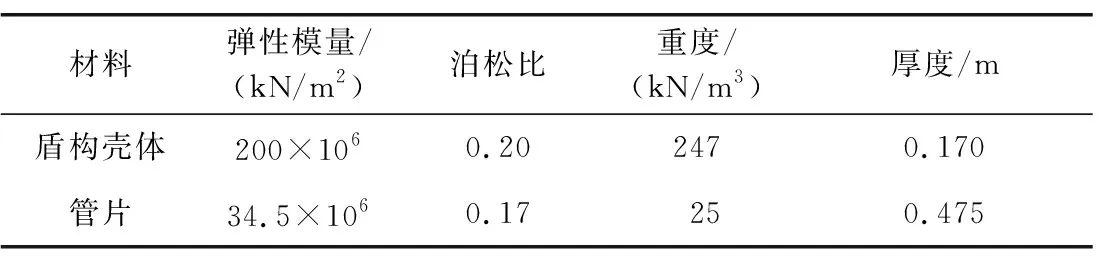
表3 隧道结构材料参数表Table 3 Material parameters of tunnel structure
土层分布: 从地表向下依次简化为厚1.5 m②1粉质黏土、厚5.5 m②y淤泥质粉质黏土、厚13 m④1粉质黏土、厚10 m⑤1粉质黏土、厚5 m⑦1粉质黏土、厚7 m⑦2粉土夹粉砂,见图4。

图4 隧道及土层模型(单位: m)Fig. 4 Model of tunnel and soil (unit: m)
边界条件: 盾构隧道-周边建筑群全区段一体化模型上表面为自由约束,四周及下表面为全约束,整体模型如图5所示。

图5 盾构隧道-周边建筑群全区段一体化数值模型Fig. 5 Integrated model of shield tunnel-surrounding buildings
2.2 土体小应变硬化(HSS)模型
2.2.1 HSS模型
HSS模型是Benz等在硬化(HS)模型的基础上考虑土体在小应变区域内刚度随应变非线性变化而提出的。通过增加2个小应变参数G0和γ0.7进行模型修正,得到考虑土体应力路径与刚度相关性、同时反映小应变阶段土体刚度变化特性的本构模型[27-28]。在标准排水三轴试验下,其剪应力与轴向应变的关系与硬化(HS)模型相同,基本呈双曲线型,表达式为:
(1)
式中:ε1为轴向应变;Rf为破坏比;E50为加载模量;q为剪应力;qa为极限偏应力。
在式(1)中引入小应变参数,得到各变形阶段与应变相关的剪切刚度G,如式(2)—(3)所示。
(2)
(3)
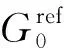
模型优势在于考虑了土体应力的历史影响及剪切硬化和压缩硬化的特性,反映了土体在小应变范围内的刚度变化特性; 与其他模型相比,在基坑和隧道施工中具有更好的适用性[25,29-30]。
2.2.2 HSS模型参数取值
由于HSS模型参数较多,试验方法较复杂[31],在实际工程中往往难以直接获得参数取值,常用经验法获取,即通过压缩实验得到压缩模量Es,再按比例计算转化为所需参数[32],具体参数取值如表4所示。

表4 HSS模型参数取值方法Table 4 Methods of parameters acqusition of HSS model
通过经验系数及地勘报告提供的压缩模量Es得到模型参数的初始值,并结合数值模拟和监测数据,参考张晋勋等[33]所提模型参数敏感性,通过工程试验段实时动态反演,进行HSS参数修正。
由于土体在荷载作用下并未发生破坏,在修正过程中模型的有效黏聚力、有效内摩擦角、剪胀角及破坏比等强度参数对最终变形结果影响极小。在该工况下,土体未过多产生刚度增加现象,刚度应力水平相关幂指数m对沉降变形量的影响并不敏感。刚度参数E50、Eoed、Eur对地表沉降量的影响较大。其中,E50及Eur与沉降量成反比,Eoed与沉降量成正比,E50对地表沉降量的敏感性最高。小应变参数G0主要影响隧道衬砌拼接后沉降回弹量与沉降量的比例关系,随着G0的增加,回弹比例逐渐减小。
HSS模型计算参数选取: 通过试验段参数实时动态反演,修正得到符合苏州地区土层变形特性的HSS模型参数,如表5所示。
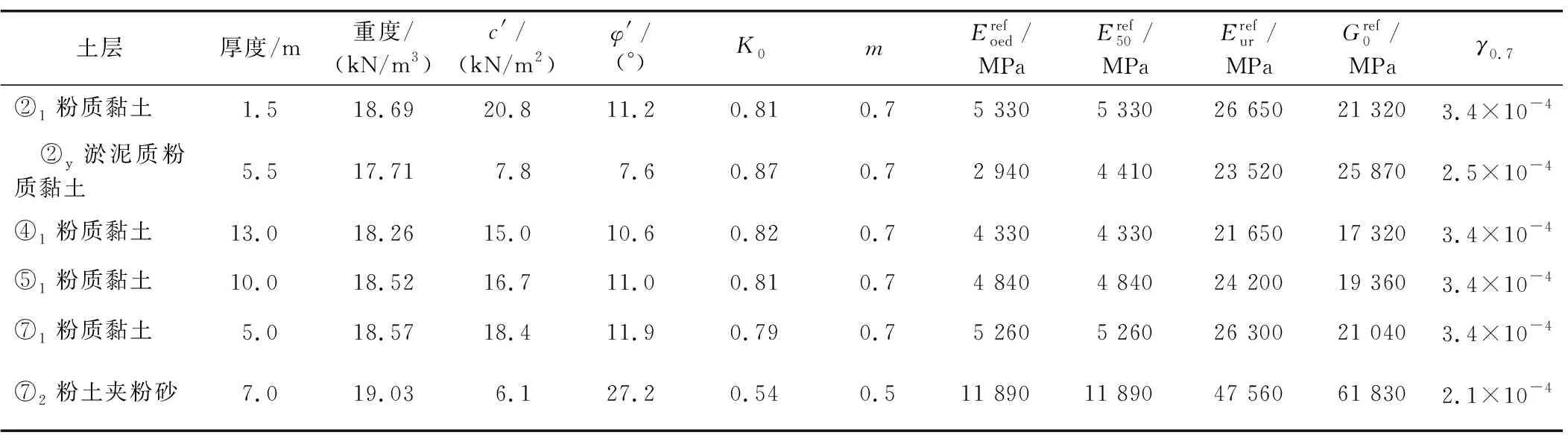
表5 HSS模型参数取值Table 5 Modified parameters of HSS model
2.3 模拟流程及方法
在盾构隧道顶进过程中,盾构注浆压力、掌子面压力及推进力3个施工因素对周边环境变形的影响较大,因此建立如图6所示的盾构模型。

图6 盾构数值模型Fig. 6 Numerical model of shield
由于模拟范围较大,土层存在不均匀性,单一的土层参数难以准确模拟实际情况,同时本工程建筑信息较为复杂,存在前期土层注浆加固、结构改造与老化、基础信息不全等不利因素,对模型的精确性产生较大影响。因此基于现场实测数据所示实时动态修正参数的研究方法,计算流程如图7所示。采用该方法基于土体试验参数和设计参数建立初步模型; 根据试验段地表沉降实测值,修正土体HSS模型参数,得到试验段模型; 在该模型基础上,针对下穿建筑物的预测段,分别通过每周的建筑测点实测值、地表沉降实测值、盾构顶进技术参数的调整等信息,将模拟段沉降值与实测沉降值进行拟合,对建筑基础参数、土体模型参数、盾构模型参数进行二次修正,得到预测段模型,即盾构隧道-周边建筑群全区段一体化三维数值模型。

图7 计算流程图Fig. 7 Calculation flowchart
3 盾构施工引起的地表及建筑物沉降影响分析
在盾构顶进过程中,地层与建筑物的变形主要表现为竖向沉降,分别对隧道横纵断面的地表沉降、建筑物关键点位沉降、左右线隧道沉降情况进行分析。
3.1 隧道横断面方向地表沉降分析
选取高风险建筑长城宾馆东侧剖面1横断面进行监测点分析,监测点位如图8所示,共包含13个监测点位。
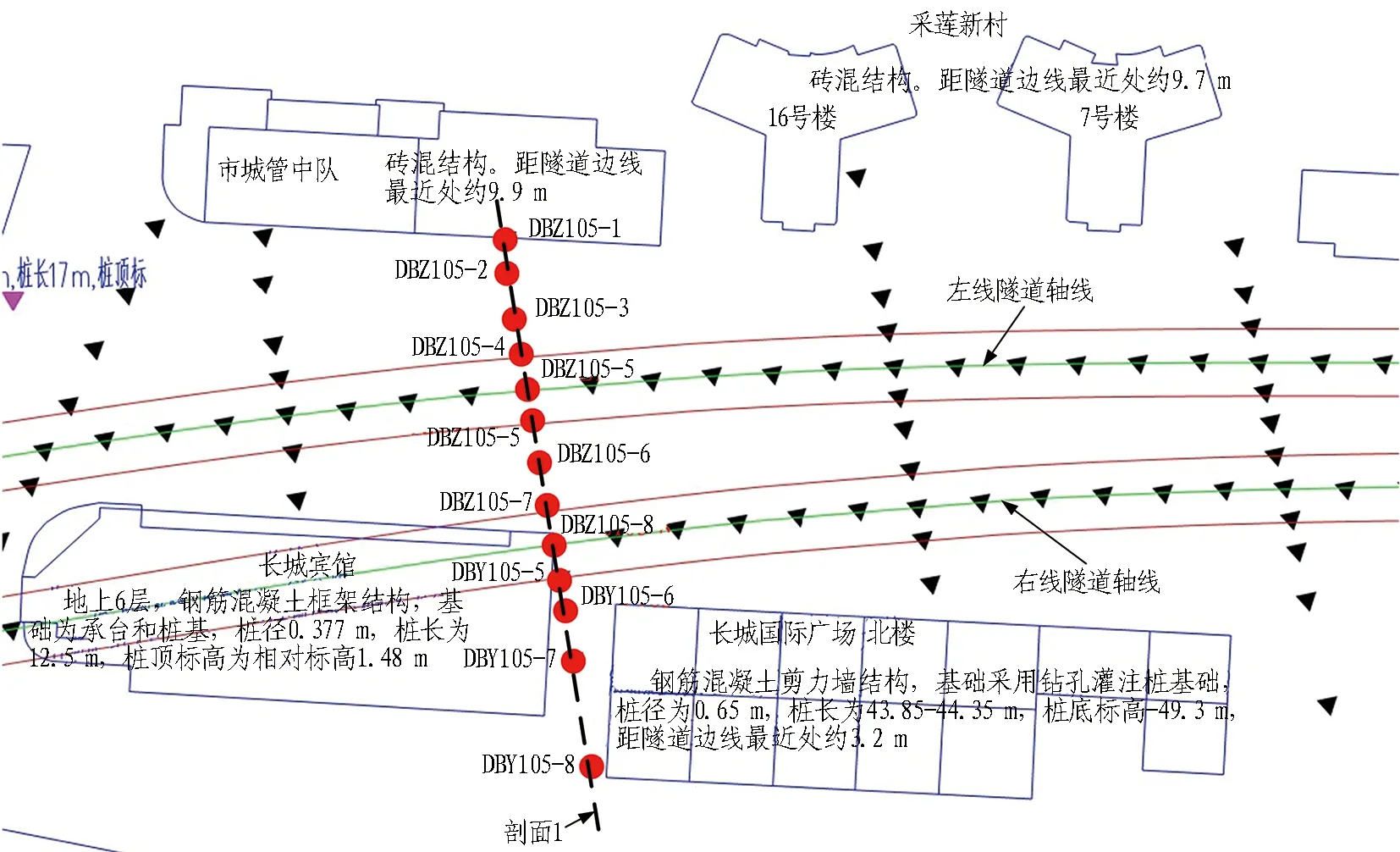
图8 剖面1横断面监测点位图Fig. 8 Monitoring points of cross-section 1
图9为左右双线盾构依次顶进到不同位置时的工况状态。其中,图9(a)中的工况1为左线开挖至200环阶段,此时右线尚未开挖; 工况2为左线开挖至930环,此时右线已开挖至200环。
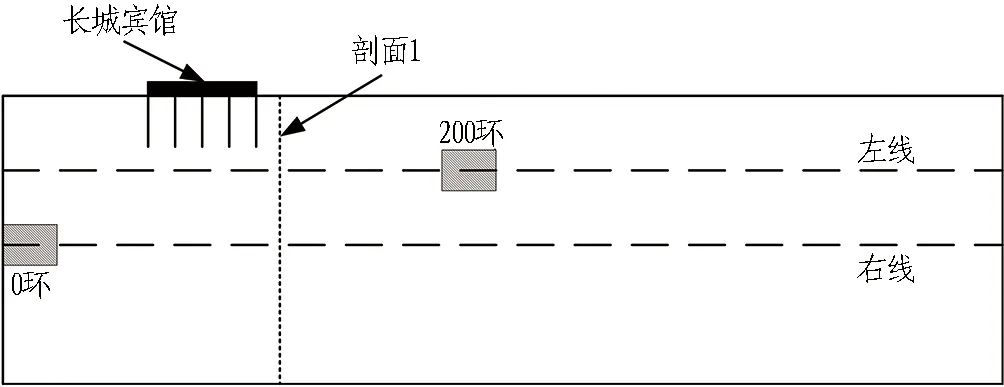
(a) 工况1
(b) 工况2图9 盾构顶进关键工况示意图Fig. 9 Schematic of critical working conditions
图10为2种工况下剖面1横断面地表沉降变形实测曲线与数值模拟曲线图。由图可知,工况1左线隧道开挖引起地表最大沉降模拟值为9.51 mm,实测最大沉降12.53 mm,均发生在左线隧道轴线上方测点DBZ105处; 工况2左右线盾构依次掘进后,引起地表最大沉降模拟值为11.28 mm,实测值为15.22 mm,最大模拟值和最大实测值均位于左右线中部区域的测点DBZ105-5处。2种工况的沉降曲线均呈“V”形,符合刘波等[7]提出的双线并行隧道Peck公式。左线隧道沉降明显大于右线的原因是: 左线盾构开挖掘进首次产生应力释放,与右线隧道二次应力释放相比,应力释放率更高。实测值与数值模拟结果规律一致,考虑实际施工因素,数值差距在合理范围内,验证了本模型的适用性。
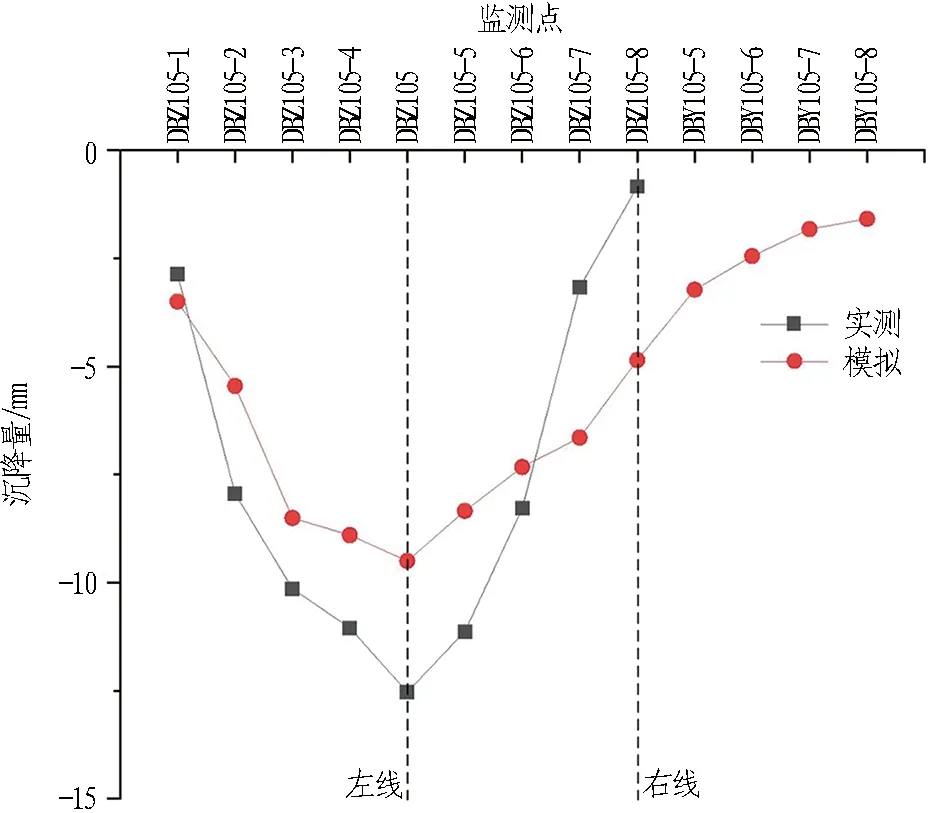
(a) 工况1
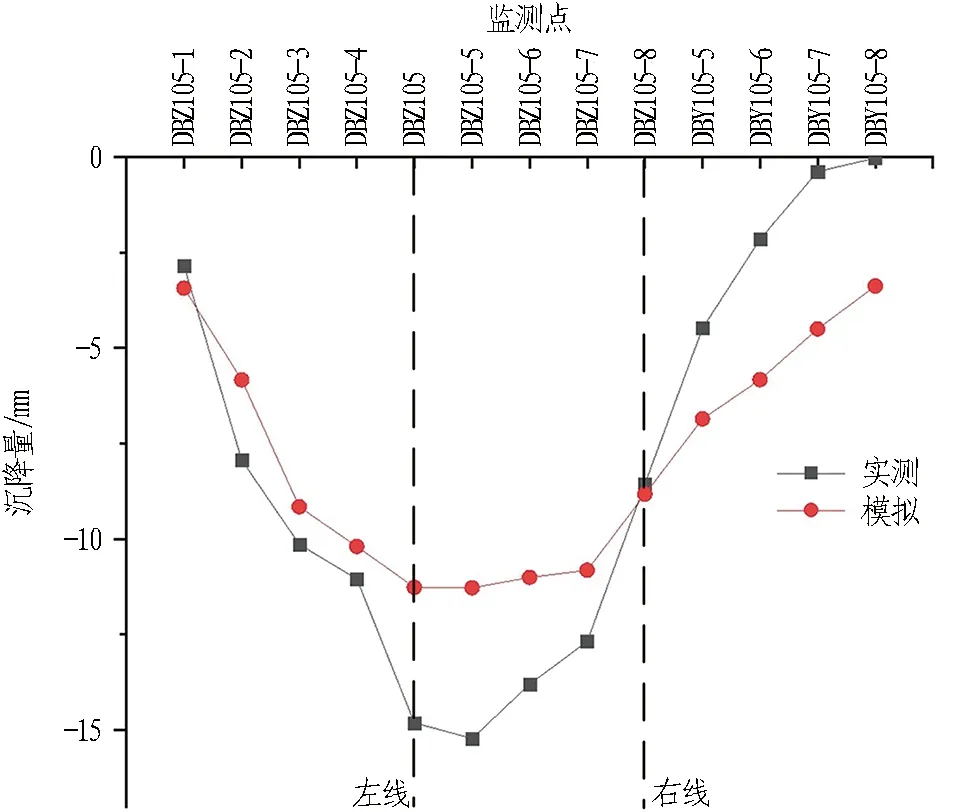
(b) 工况2图10 剖面1横断面地表沉降曲线Fig. 10 Subsidence curves of cross-section 1
3.2 隧道纵断面方向地表沉降分析
为分析盾构施工引起周边变形的影响范围,以盾构左线经过危险建筑长城国际广场时的进度115环为例,选取位于隧道左线正上方的关键剖面2进行沉降分析,如图11所示,共8个监测点。

图11 剖面2纵断面监测点位图Fig. 11 Monitoring points of longitudinal cross-section 2
剖面2纵断面地表沉降曲线如图12所示,最大变形量可达16.2 mm,主要发生在隧道掌子面与盾构掘进反方向35环(约40 m)范围。

图12 剖面2纵断面地表沉降曲线(左线)Fig. 12 Subsidence curves of longitudinal cross-section 2 (left line)
3.3 地表沉降随盾构掘进发展规律
在盾构掘进过程中,地表最大变形位于隧道轴线上方,同时考虑盾构施工对高风险建筑的影响,选取隧道左线上方测点DBZ75、右线上方测点DBY125进行沉降分析,监测点位布置如图13所示。
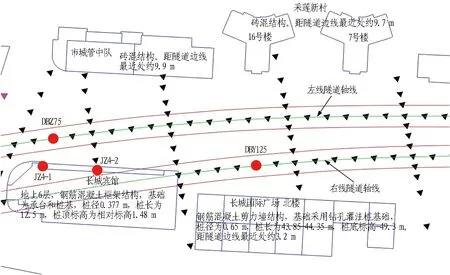
图13 关键监测点位布置图Fig. 13 Locations of critical monitoring points
监测点地表沉降量变化曲线如图14所示,图中变形量负值代表沉降,正值代表隆起。
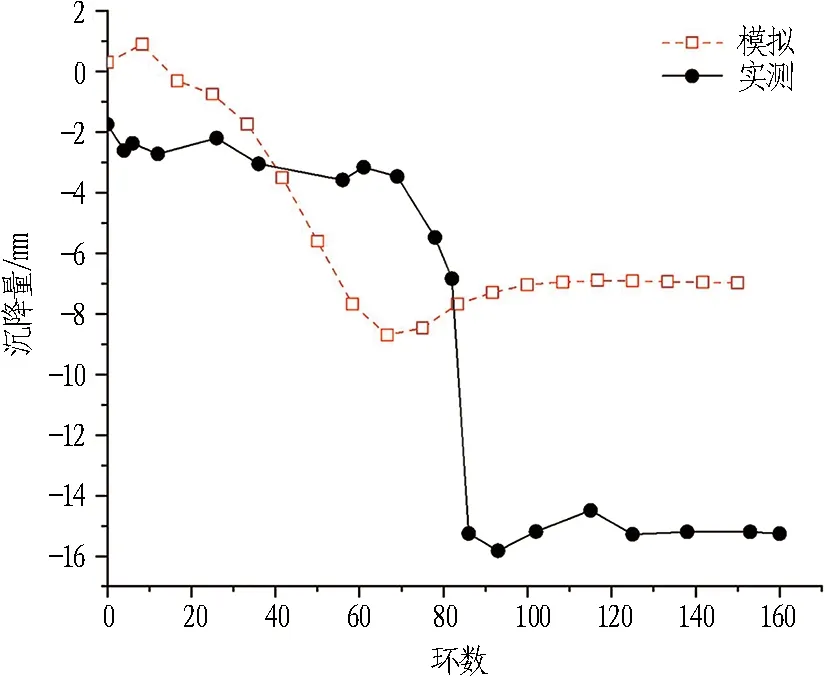
(a) 左线隧道地表测点DBZ75
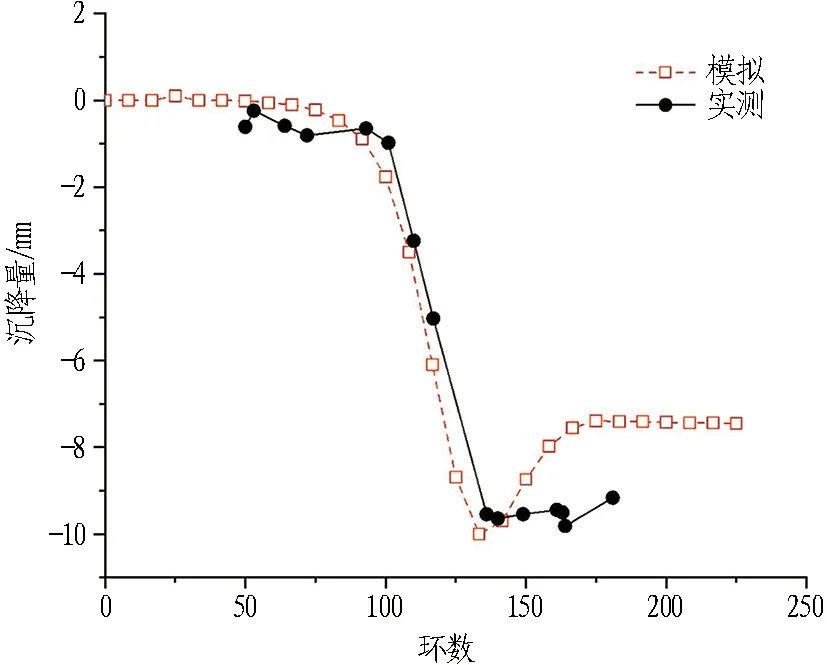
(b) 右线隧道地表测点DBY125图14 地表沉降量变化曲线图Fig. 14 Settlement curves of ground surface
在模拟过程中设置盾构单位顶进长度为10 m,由此导致变形影响区域有所提前; 对于隧道上方地表测点,模型未考虑施工时地面道路正常通行的车辆荷载,场地堆载等因素,因此,图14(a)、 (b)地表监测点实际沉降值大于模拟沉降值,如左线隧道地表测点DBZ75的实测沉降值最大可达16 mm,模拟最大沉降值约为8.8 mm; 右线隧道地表测点DBY125,实测最大沉降值约为10 mm,模拟值接近,略偏小,左线隧道盾构掘进引起的地表沉降明显大于右线隧道。
由图14可知,随着盾构顶进,地面沉降曲线呈勺形变化。变形可分为如图15所示的4个阶段。
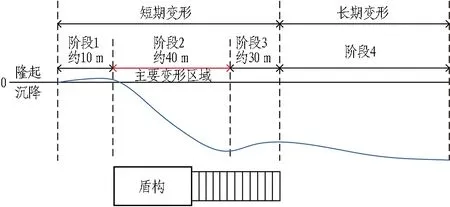
图15 盾构隧道地表沉降发展阶段示意图Fig. 15 Stages for surface settlement development of shield tunnel
阶段1: 盾构前方土体受到盾构顶进力作用,在掌子面压力的作用下土体产生少量变形。当掌子面压力偏大时,土体在掌子面压力作用下向盾构前部堆积,地表产生隆起现象; 当掌子面压力偏小时,土体向盾构内部方向塌陷,地表产生沉降现象。由于该阶段变形量与盾构推进时的掌子面压力有关,实际施工中顶进力因时调整,而模拟中参数根据施工日志调整。本模拟工况为隆起变形,变形量为0~2 mm; 实测地表变形量为-4~3 mm。
阶段2: 盾构对土体进行切削注浆并对管片进行拼接,由于刀盘切削土体,以及刀盘尾部、注浆段及管片之间存在间隙造成大量地层损失,最终导致地面出现大量沉降。模拟最大沉降值约为18 mm,实测最大沉降值约为16 mm。
阶段3: 在管片完成拼接后,由于地应力逐步释放,同时管片具有较大刚度,导致隧道结构及上部土体出现上浮现象,已有沉降量出现回弹,模拟与实测回弹量较为接近,均为1~2 mm。
阶段4: 由于土体被扰动后的二次固结作用,地表会出现持续且较为缓慢的下沉过程,该阶段变化量较小,模拟大小为0.5~1 mm,而实际工况中土体自然固结过程较为缓慢,变形并不明显。
3.4 周边建筑物沉降随盾构掘进发展规律
针对盾构掘进对周边建筑物的影响,选取长城宾馆测点JZ4-1、JZ4-2作为研究对象。由于基础形式的简化及结构资料的缺失,风险分析时考虑将建筑荷载取较大值,同时实测中建筑沉降监测点位于建筑结构上,地层变形引起的沉降敏感性较差。因此,图16中建筑测点沉降模拟值大于实测值,最大模拟沉降量可达12 mm,而最大实测值约为8 mm。
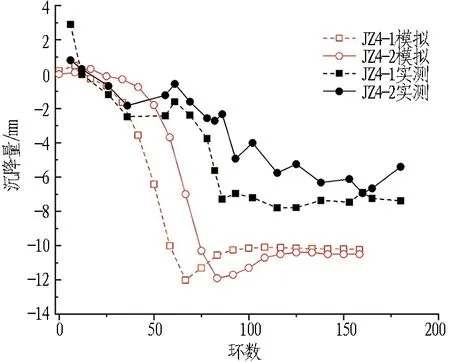
图16 建筑物关键监测点沉降量变化曲线图Fig. 16 Settlement curves of critical mornitoring points of building
3.5 隧道左右线依次掘进对比分析
本工程区间盾构采用左右两线依次掘进,当左线盾构推进至730环(约880 m处)时再进行右线推进,由3.3节和3.4节可知,左线盾构推进引起的沉降已达到较为稳定的状态,此时进行右线开挖对邻近建筑存在二次风险。选取建筑监测点JZ4-1研究沉降变化规律,图17(a)为剖面1沉降达到稳定阶段时,左线开挖200环(右线未开挖),右线开挖200环(右线已开挖至930环)2个阶段沉降对比图,左右线依次掘进后的剖面1横断面沉降曲线呈“W”形。由于地应力二次释放原因,右线模拟值和沉降值均明显小于左线。由于模型未考虑施工时地面道路正常通行的车辆荷载,场地堆载等因素,因此左右两线实测值均大于模拟值,左线实测值最大可达12.5 mm。长城宾馆监测点JZ4-1模拟曲线呈勺形变化规律,与横断面规律一致,左线隧道掘进引起的模拟和实测沉降值大于右线隧道,左线实测沉降值约8 mm,模拟沉降值约为12 mm,左线模拟值大于实测值,而JZ4-1测点靠近右线隧道,会出现沉降实测值略大于模拟值。
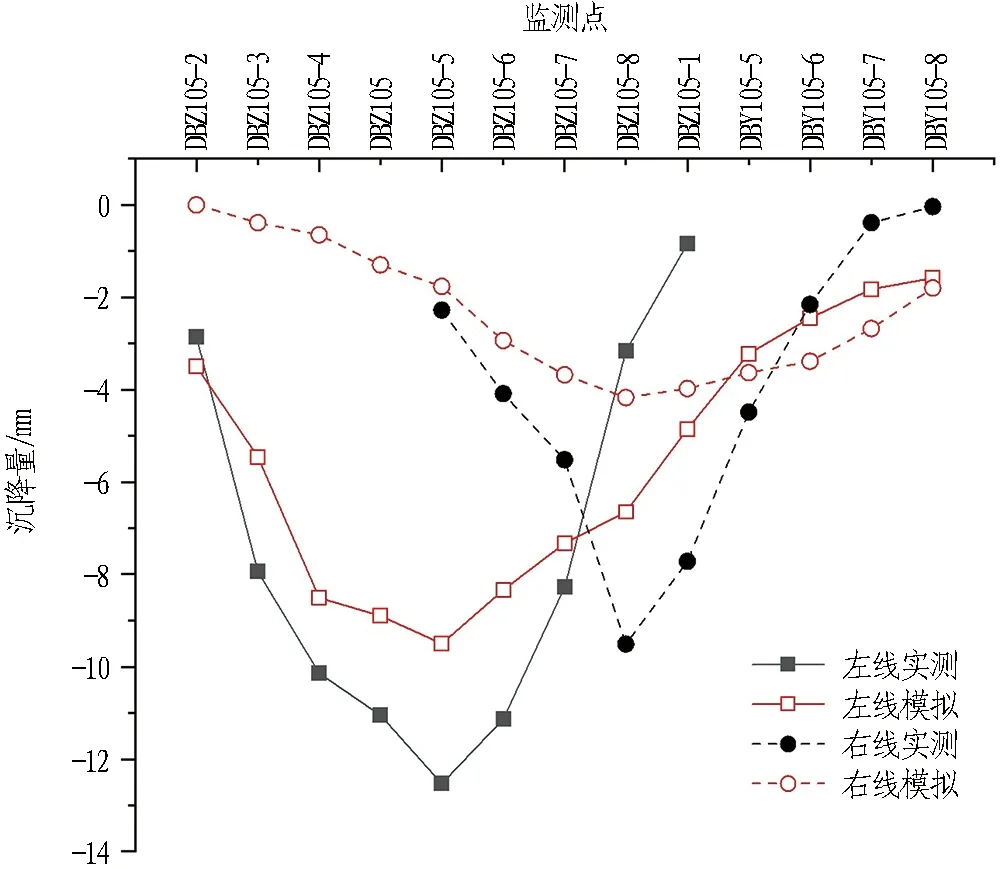
(a) 剖面1横断面地表沉降
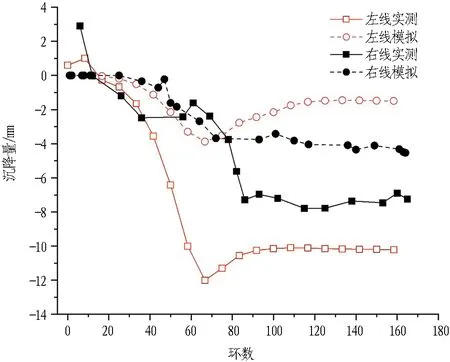
(b) 长城宾馆监测点JZ4-1图17 建筑物关键测点及剖面沉降曲线对比Fig. 17 Settlement comparison of critical points and section of building
对于其他高风险建筑,建筑物最大沉降实测值如表6所示。
根据建筑物沉降情况,除长城宾馆因施工因素在右线掘进中沉降量偏大外,其余测点由于已经完成左线开挖,地应力已经初步释放; 左线隧道的荷载对于土体产生了进一步固结作用,因此沉降量控制在较小范围内。而左线隧道管片结构也对土体产生了一定的加固作用,且由于先掘进左线隧道时采取了注浆加固等施工措施,故导致右线掘进时引起的沉降变化量小于左线掘进。而长城广场和第一人民医院由于与右线隧道距离接近,右线隧道掘进引起的沉降值略大于左线顶进,通过盾构全区间模拟与实测发现,右线隧道模拟和实测沉降量为左线的50%~70%。
4 结论与建议
1)建立了基于HSS本构模型的区间隧道-周边建筑群全区段一体化三维数值模型,提出了一套基于现场实测数据进行实时动态修正参数的研究方法,通过苏州地铁工程实例验证了工程适用性。
2)基于未下穿建筑物的试验段数值模型和地表沉降实测值,可反演得到一套适用当地土层的HSS模型修正参数;在该HSS模型基础上,针对下穿建筑物的预测段,分别通过建筑测点实测值、地表沉降实测值、盾构技术参数的调整等信息,对建筑基础参数、土体模型参数、盾构模型参数进行二次修正,拟合效果较好。
3)对于直径6 m的圆形盾构掘进,引起软土地层地表及周边建筑物主要的沉降变形影响范围在隧道掌子面沿掘进方向50环与掘进反方向35环区间内。建筑物基础由于存在早期注浆加固等施工措施,实测沉降量一般小于模拟值,也小于邻近地表变形量,如长城宾馆实测最大沉降为7.38 mm,邻近地表实测最大沉降量为16.2 mm。
4)盾构左右线依次掘进对周边环境影响主要风险在于先掘进的左线隧道,后掘进的右线隧道产生的变形量明显偏小,在力学机制上与地应力的初次和二次释放有关,也与先掘进左线隧道时采取的注浆加固等施工措施相关,通过盾构全区间模拟与实测发现,右线隧道模拟和实测沉降量为左线的0.5~0.7倍。
针对双线区间盾构隧道施工,建议重点关注首条盾构开挖引起的地层变形,尤其是开挖面前50环、后35环区间范围内的地层变形情况。

