平行4孔山岭隧道渗流场解析解及影响参数分析

李鹏飞， 刘 江， 张素磊

(1. 北京工业大学 城市与工程安全减灾教育部重点实验室， 北京 100124； 2. 青岛理工大学土木工程学院， 山东 青岛 266033)

0 引言

近年来，随着中国城市化进程的推进及经济区域化趋势的发展，出现了越来越多的平行4孔山岭隧道工程[1-2]。在隧道修建过程中不可避免会遇到富水地层，而地下水渗流会给隧道施工带来断面涌水、渗透水压过大等问题。因此，隧道渗流场一直是国内外学者的研究热点[3-4]。

解析法具有物理概念清晰、计算简捷等优点，备受学者们青睐。Harr[5]最早提出使用镜像法，并运用该方法求得了适用于深埋高水头圆形洞室的围岩孔隙水压力计算公式。应宏伟等[6]采用镜像法将半无限渗流场转化为2个虚拟无限渗流场的叠加，推导了考虑注浆圈作用的水下大埋深隧道渗流场的解析解。王建宇[7]将圆形隧道近似为轴对称模型，根据达西定律和竖井理论推导了隧道孔压分布和渗流量近似解。王秀英等[8]在轴对称模型的基础上进一步推导了山区高水位隧道衬砌、注浆圈外水压力的表达式。Park等[9]利用复变函数保角变换，将半无限域渗流场转换为圆环域渗流场进行求解，通过假设不同的边界条件分别得到若干特定条件下的解析解。朱成伟等[10]基于稳态渗流控制方程，结合保角变换法，推导了适用于任意埋深的水下衬砌隧道渗流场的解析解。赵建平等[11]以复势函数和地下水力学理论为基础，引入双极坐标描述等势线，推导了作用在富水区隧道支护结构上的水头、渗流量的计算公式。

对于多孔隧道，张丙强[12]以镜像法和渗流力学理论为基础，推导了考虑注浆圈与初期支护时，半无限平面双孔近距离平行隧道稳定渗流场的解析解。Wang等[13]基于镜像法与叠加原理,针对隧道洞周等水头、等水压2种不同的边界条件，分别推导了对称双线隧道孔隙水压力分布与渗流量解析解。朱成伟等[14]结合保角变换法与叠加法，对双线隧道稳态渗流场进行了推导，得到了双孔隧道渗流场解析解。王帅等[15]运用镜像法在单孔隧道渗流的基础上推导了平行3孔海底隧道渗流场解析解。

目前，隧道渗流场研究多数集中于单孔隧道，而对于多孔隧道尤其是隧洞数量较多的山岭隧道渗流场，相关研究并不完善。本文基于稳态渗流理论，结合镜像法推导平行4孔山岭隧道渗流场解析解，结合前人研究与数值模拟对其进行对比验证，并利用该解研究隧道间距、相对尺寸、初期支护参数等因素对隧道涌水量及初期支护后水压力的影响规律。

1 渗流场解析解

1.1 计算模型

半无限平面内平行4孔圆形隧道简化模型如图1所示，模型介质包含围岩、初期支护和二次衬砌3部分。图中，隧道从左到右依次命名为隧道1、隧道2、隧道3、隧道4；ri、rli、rci分别为隧道净空半径、二次衬砌外径、初期支护外径，i=1、2、3、4，分别对应隧道1—4；b1、b2、b3分别为两两相邻隧道间的水平间距；为方便后续计算表达，在围岩中任取一点，d即为该点的埋深，d1、d2、d3、d4分别为隧道1、2、3、4圆心与该点的竖向间距；H为以该点起算的水头。对计算模型作如下假设： 1)隧道纵向长度远大于截面尺寸； 2)隧道围岩和衬砌均为各向同性均匀连续介质，地下水以孔隙水的形式赋存于围岩中，且在渗流过程中水面保持不变； 3)渗流方向以径向为主，隧道排水通过衬砌均匀渗水实现，忽略隧道内侧位置水头的影响； 4)渗流场为稳态渗流，渗流符合达西定律及质量守恒定律。

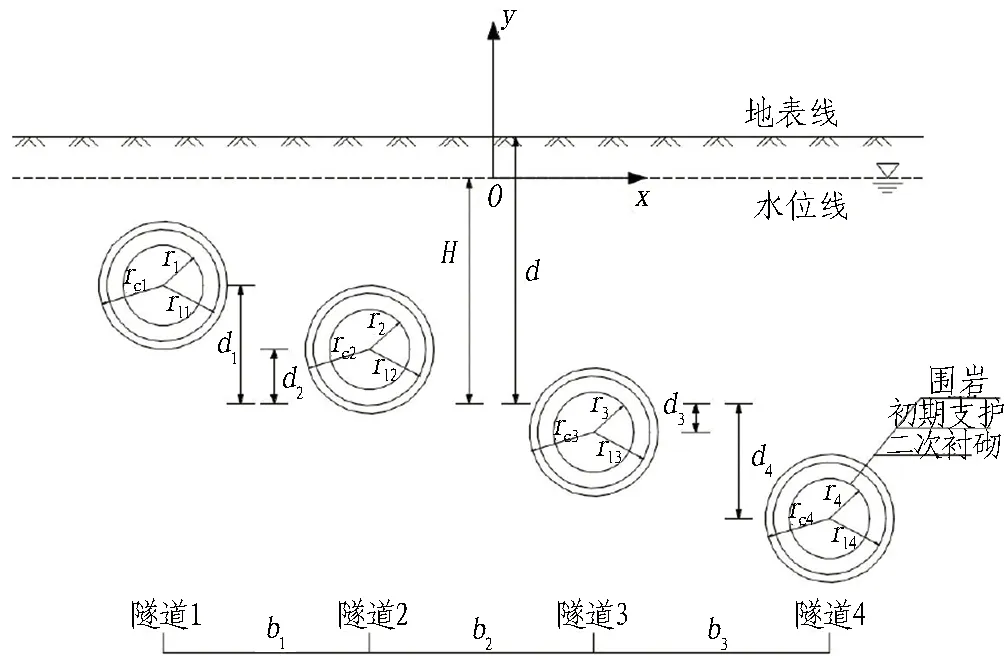
图1 平行4孔隧道渗流场计算模型Fig. 1 Seepage field calculation model of parallel four-tube tunnel

1.2 解析思路

针对半无限平面内4孔平行隧道渗流场的特点，本文考虑综合采用镜像法及叠加原理对该问题进行求解，具体求解过程如下：

1)根据镜像法原则，对图1所示的半无限平面4孔平行隧道渗流问题进行转化，以水位线为等势面对真实隧道进行映射，在对称位置形成虚拟隧道，如图2所示，两侧隧道流量大小相等，方向相反。

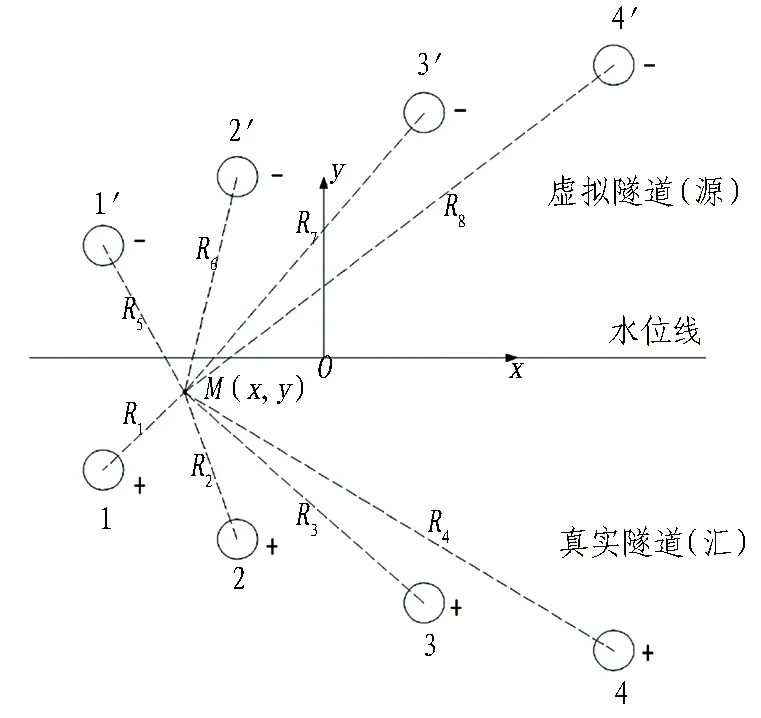
图2 镜像法示意图Fig. 2 Schematic of image method

2)根据渗流理论，对无限平面内单孔隧道渗流问题进行求解，得到任意一点的水头势函数。

3)根据叠加原理，无限平面内任意一点的水头势可以相互叠加，据此将半无限平面内4孔平行隧道渗流场转化为无限平面内8孔隧道渗流场的叠加，并根据边界条件确定待求系数。

1.3 水头势函数

在均质各向同性介质中，根据达西定律和质量守恒定律，可得二维稳定渗流问题的控制方程为拉普拉斯方程：

(1)

根据渗流力学原理，可将式(1)转化为极坐标下的表达形式[16]：

(2)

式(1)—(2)中：r为渗流半径；φ为无限平面内渗流场水头势函数。

根据达西定律，流经圆形隧道每一断面的流量Q可以表示为

(3)

式中k为介质渗透系数。

对式(3)进行积分，可以得到单孔隧道在无限平面渗流场内任意一点的水头势函数φ：

(4)

式中：Qi为隧道i的涌水量；C为待定系数。

根据叠加原理，无限平面8孔隧道围岩内任意一点M的水头势函数为

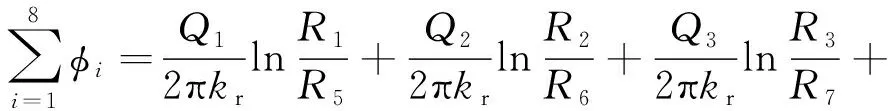
(5)

式中：R1、R2、R3、R4、R5、R6、R7、R8分别为无限平面内任意点M至各隧道中心点的距离；kr为围岩的渗透系数。

1.4 毛洞涌水量解析解

在毛洞状态下，取各隧道净空半径为ri，根据图2中各隧道几何位置可求得R1—R8。当M点位于水位线平面时(R1=R5,R2=R6,R3=R7,R4=R8)，水头为H，将此边界条件代入式(5)中可得C=H。根据上述参数，平行4孔隧道中各隧道内边界水头分别为：

(6)

(7)

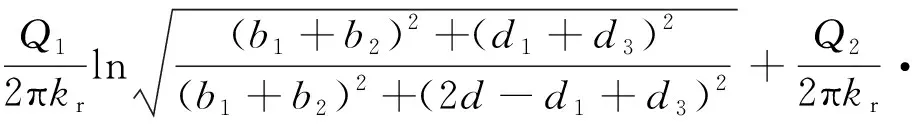
(8)

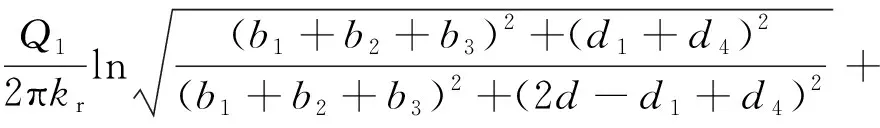
(9)

将式(6)—(9)联立可解得半无限平面内4个平行隧道毛洞状态下各自隧道的涌水量计算式分别为：

(10)

(11)

(12)

(13)

式(10)—(13)中：

Q0=A2F2+B2E2+C2D2-A2γη-B2βη-C2βγ-D2αη-E2αγ-F2αβ+2ABDη+2ACEγ+2BCFβ+2DEFα-2ABEF-2ACDF-2BCDE+αβγη；

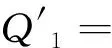
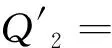
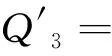
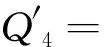
其中，

1.5 考虑衬砌时涌水量解析解

根据本文假设，隧道施作衬砌完成后，衬砌内渗流依然符合渗流方程，故在初期支护区域内对式(3)进行积分可得

(14)

式中：Qci为隧道i围岩与初期支护界面处涌水量；kc为初期支护的渗透系数；Hci、Hli分别为初期支护、二次衬砌外表面水头。

根据渗流连续性准则，地下水流经各断面的流量相等，即

Qci=Qi。

(15)

目前，为满足防排水要求，山岭隧道通常采用复合式衬砌，即在初期支护与二次衬砌间设置防水层与排水系统，地下水渗入初期支护后直接通过排水系统排出隧道外。本文假设复合式衬砌正常发挥作用，即隧道二次衬砌不透水，则二次衬砌外表面水头Hli=0，且隧道内净空水头Hi=0。令式(6)—(9)中各隧道净空半径ri等于各隧道初期支护半径rci，然后与式(10)—(15)联立求解，可以得到考虑复合式衬砌影响时4条平行隧道的涌水量计算公式分别为：

(16)

(17)

(18)

(19)

式(16)—(19)中：

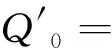
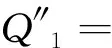
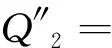
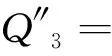
其中，

将式(16)—(19)代入式(14)可以求得Hci，进而得到初期支护后水压力

(20)

式中γw为水的容重。

2 解析解验证

2.1 退化为单孔隧道

若b1=b2=b3=∞，d1=d2=d3=d4=0，则可认为4条隧道分布于同一水平线且各自可视为单孔隧道。假设各隧道半径均相同，且对应围岩及初期支护渗透系数也相同，则此时可得到A=B=C=D=E=F=0，a=b=c=d，式(16)—(19)可简化为：

(21)

退化为单孔隧道后，式(21)与文献[6]仅考虑衬砌时单孔隧道解析解相同，从而初步验证了本文解析解的正确性。

2.2 退化为双孔隧道

当隧道2、隧道3、隧道4的水平间距趋向于无穷大时，隧道3、隧道4可分别近似视为单孔隧道，隧道1、2可共同视为半无限平面内的双孔隧道。基于此，本节取b2=b3=2 500 m，此时可视为b2、b3趋向无穷大，其余参数与文献[12]中参数一致，即隧道半径为5 m，埋深为45 m，水位线高度为36 m，根据式(10)—(13)可求得4条平行隧道不施加支护时的涌水量分别为4.42、4.42、6.76、6.76 m3/(m·d)，隧道1、2涌水量结果与文献[12]中解析解结果一致，隧道3、4涌水量结果与单孔隧道涌水量相同，说明本文解析解退化为双孔隧道时计算正确，由此证明本解析解推导的正确性。

2.3 退化为3孔隧道

当隧道1与隧道2的水平间距b1趋于无穷大时，可将隧道1近似视为单孔隧道，剩余隧道可视为半无限平面内的平行3孔隧道。本节取b1=2 500 m，此时可视为b1近似无穷大，其余参数与文献[15]中所取参数一致，即隧道半径均为5 m，覆土厚度为40 m，海水深度为25 m，隧道间距均为20 m，同样根据式(10)—(13)可求得4条平行隧道不施加支护时的涌水量分别为65.7、41.2、22.2、41.2 m3/(m·d)，隧道1涌水量与单孔隧道涌水量相同，其余隧道涌水量与文献[15]中各隧道涌水量计算结果相同，该对比进一步说明了本文推导解析解的正确性。

2.4 数值验证

本节以余姚市某4线公路隧道为背景，依据面积等效原则将隧道断面形状简化为圆形，并采用FLAC3D建立如图3所示数值模型，对理论推导得到的解析解结果进行验证。该模型尺寸为200 m×1 m×100 m(长×宽×高)，模型中包含4条平行隧道，其中位于外侧的隧道1、隧道4净空半径均为2 m，初期支护厚0.3 m，位于中部的隧道2、隧道3净空半径均为5 m，初期支护厚0.5 m，4条隧道埋深均为45 m，水平间距b1=b3=17 m，b2=25 m，围岩边界水位线高度为35 m。围岩渗透系数为5×10-6m/s，初期支护渗透系数为5×10-8m/s。在采用位移边界条件后，设置四周及底部边界为不透水边界，顶部边界及隧道内边界为透水边界，并固定隧道内边界孔隙水压力为零。水位线下围岩为饱水地层，水压随深度呈现梯度变化，通过FLAC3D内置Fish函数，取单位长度隧道外围节点的不平衡流量之和，以此作为隧道的涌水量[17]。

图3 数值计算模型Fig. 3 Numerical calculation model

对比本文解析解与数值解(见表1)可知，二者吻合较好，验证了本文解析解的正确性。

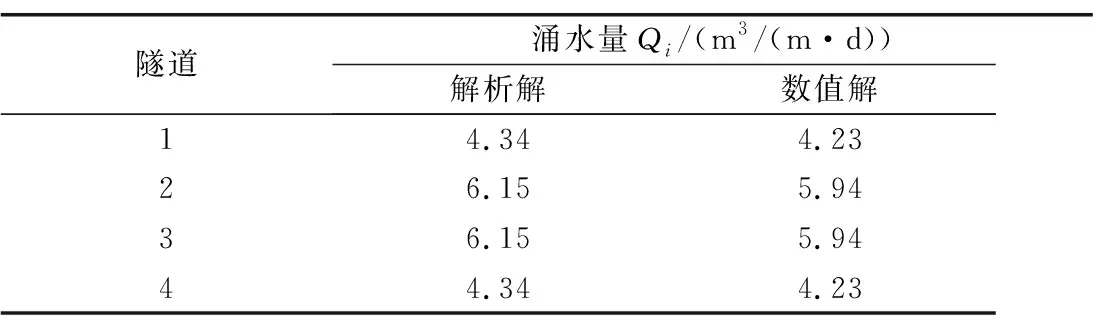
表1 解析解与数值解对比Table 1 Comparison between analytical and numerical solutions

3 影响参数分析

不同于单孔隧道渗流场，在研究4孔隧道时需考虑隧道间的相互影响，故本节将对隧道间距、隧道相对大小、初期支护情况等参数进行影响分析。为了弱化研究某一参数对隧道渗流场的影响规律时其他参数的干扰作用，本节对2.4节算例中的某些参数进行适当修改： 在隧道埋深及地下水位不变的情况下，将4条隧道设置为相同半径，即r1=r2=r3=r4=5 m，初期支护厚度均设置为0.5 m，隧道间水平间距b1=b2=b3=25 m，其余参数均与数值验证一节中所采用参数一致。由于在本节所采用的大多数工况条件中4孔隧道均为对称布置，故多数分析中仅取隧道1与隧道2为研究对象，一些特殊工况下才对全隧道进行分析，后期不再赘述。

3.1 隧道间距的影响

3.1.1 水平间距的影响

为明确隧道间水平间距的变化对4孔隧道中各隧道涌水量及初期支护后水压力造成的影响，本节设置了3种工况进行讨论。1)工况1： 保持b2数值不改变，b1与b3以相同的数值变化，即固定隧道2与隧道3相对位置不变，隧道1与隧道4分别沿水平方向与隧道2、3的距离逐渐增大。2)工况2： 保持b1与b3数值不变，仅b2大小发生改变，即隧道1与隧道2、隧道3与隧道4相对位置不发生改变，隧道2与隧道3的水平间距逐渐增大。3)工况3： 保持b1、b2数值不变，仅改变b3的大小，即固定隧道1、隧道2、隧道3的相对位置，隧道4沿水平方向逐渐远离隧道1、2、3。各隧道涌水量及初期支护后水压力随水平间距的变化情况如图4和图5所示。

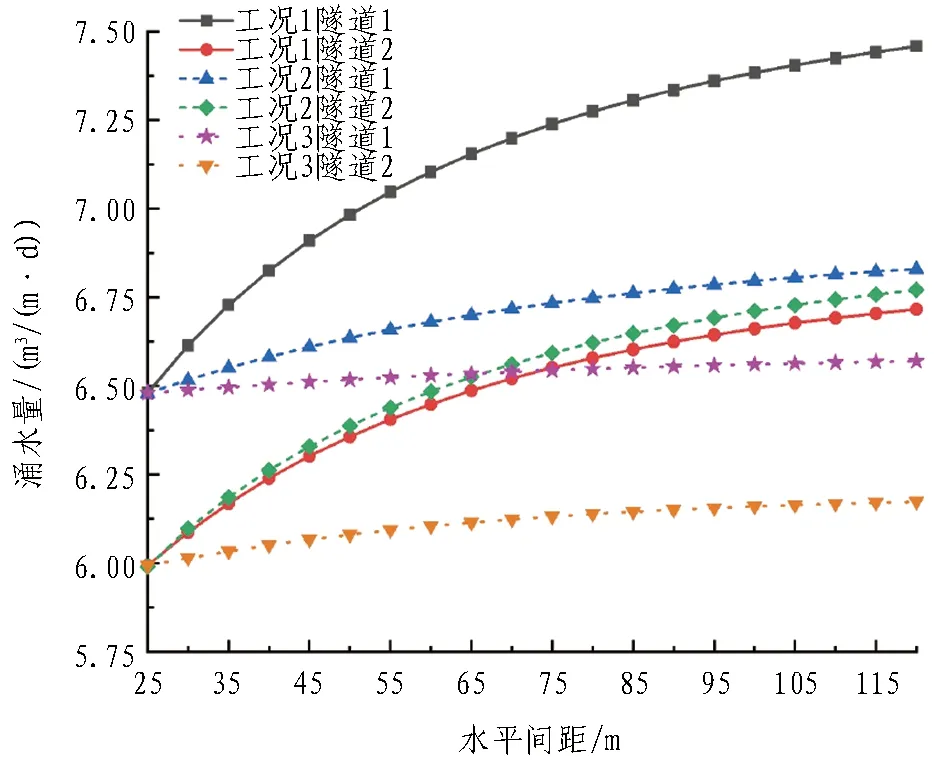
图4 隧道涌水量与水平间距的关系Fig. 4 Relationship between tunnel water inflow and horizontal spacing

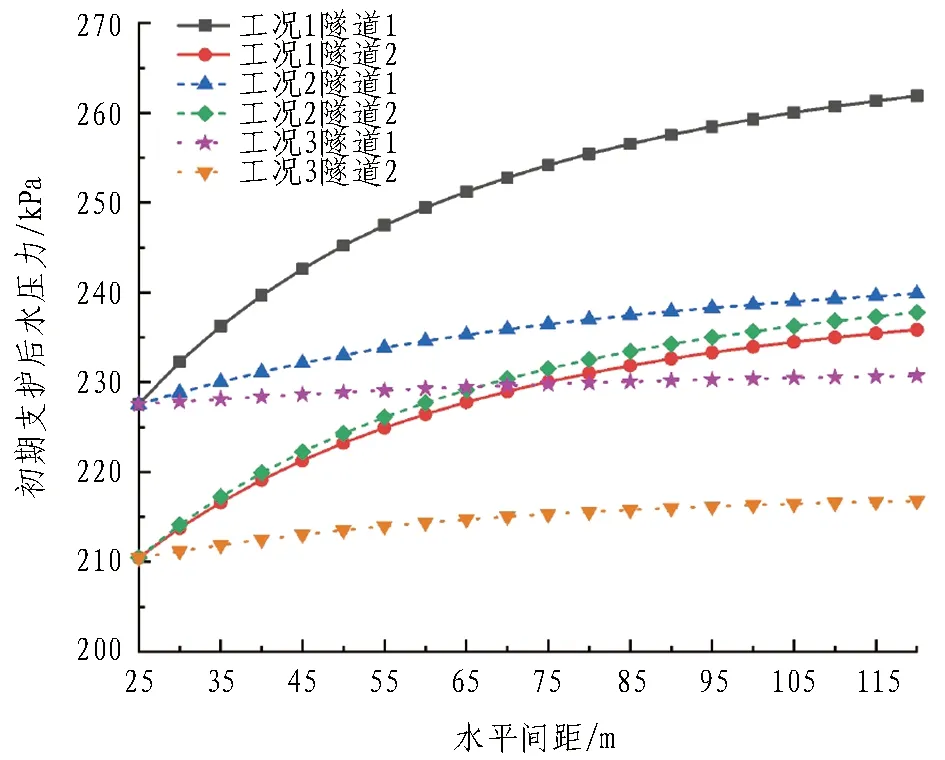
图5 初期支护后水压力与水平间距的关系Fig. 5 Relationship between horizontal spacing and water pressure after primary supporting

从图5可以看出： 1)工况1中，随着b1与b3的不断增大，隧道1与隧道2的涌水量及初期支护后水压力均逐渐增大，并且当水平间距小于100 m时，随着水平间距的增大，隧道涌水量及初期支护后水压力增长较快，当水平间距大于100 m后，增长趋势开始变缓，相似的规律在工况2、工况3中也有所体现。故对于4孔隧道渗流场，隧道间的“分流”作用随着隧道间距的增大而逐渐减小，并且在隧道尺寸相等的条件下，隧道水平间距的主要影响距离为20倍隧道半径。2)工况1时，随着隧道间距的增大，隧道1涌水量有较大的提升； 工况2时，在隧道1与隧道2间距不变的情况下，b2在相同变化范围内，隧道1涌水量的提升减弱了很多； 而工况3时隧道1、2、3间的距离不变，该变化则更加不明显。对于隧道2来说，工况1与工况2的区别在于工况1中隧道1与隧道4分属两侧同时远离隧道2，而工况2中隧道3与隧道4在同一侧远离隧道2，2种工况在相同间距变化范围内，工况2时隧道2涌水量的变化要略大于工况1，隧道初期支护后水压力也有相同的规律，本节不再赘述。由此可以看出，对于平行多孔隧道渗流场，其中某一隧道渗流场的变化更大程度上受两侧相邻隧道的影响，且同侧多孔隧道间距变化带来的影响要比异侧同等条件变化所带来的影响显著。

3.1.2 竖向间距的影响

本节通过改变不同隧道的埋深，设置了3种工况来研究隧道竖向间距带来的影响： 1)工况1，保持隧道2、3位置不变，隧道1与隧道4同时移动； 2)工况2，保持隧道1、4位置不变，隧道2与隧道3同时移动；3)工况3，保持隧道3、4位置不变，隧道1与隧道2同时移动。根据计算模型中的假设，d1与d2向下移动时取正，向上移动时取负，d3、d4则相反。图6与图7分别给出了不同竖向间距条件下隧道涌水量及初期支护后水压力的计算结果。从图6—7中可以看出： 1)竖向间距变化导致隧道埋深变化，工况1、2中，随着隧道埋深的逐渐增大，该隧道涌水量逐渐增大，而位置未发生改变的隧道涌水量则随之先缓慢减小后快速增大；工况3中，隧道1、2、3涌水量变化情况与前述规律相似，隧道4涌水量随隧道1、2埋深的增大变化较小。2)工况1条件下，当d1=-d4=-5 m时，隧道2涌水量及支护后水压力最小；工况2条件下，当d2=-d3=-5 m时，隧道1涌水量及支护后水压力最小；工况3条件下，当d1=d2=-5 m时，隧道3涌水量及支护后水压力最小。若将位置发生变化的隧道视为排水隧道，在其与主隧道水平间距不变的条件下，当位于主隧道上方约0.5倍洞径时，主隧道涌水量最小，排水效果最好。

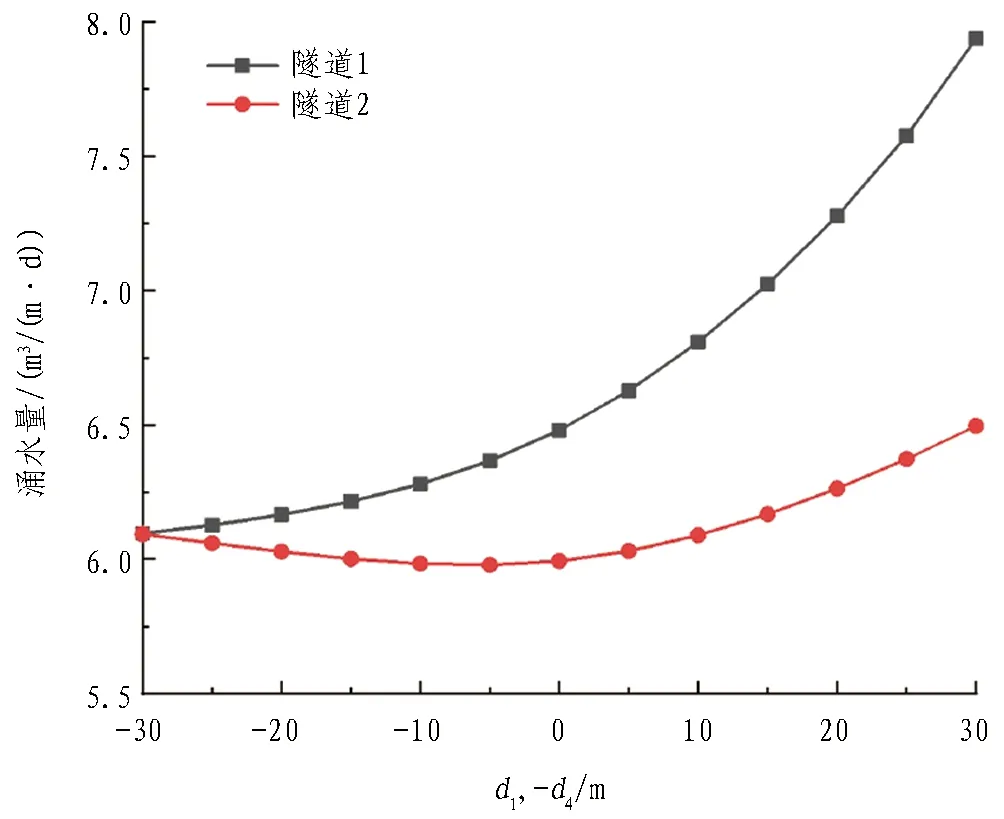
(a) d1与d4同时变化(工况1)

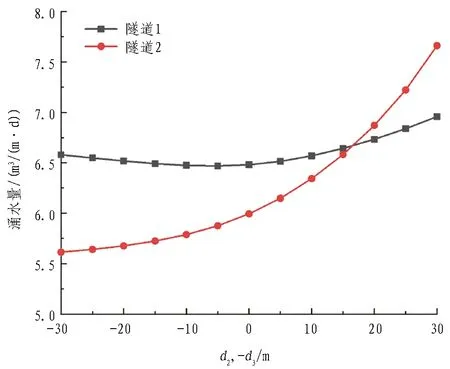
(b) d2与d3同时变化(工况2)

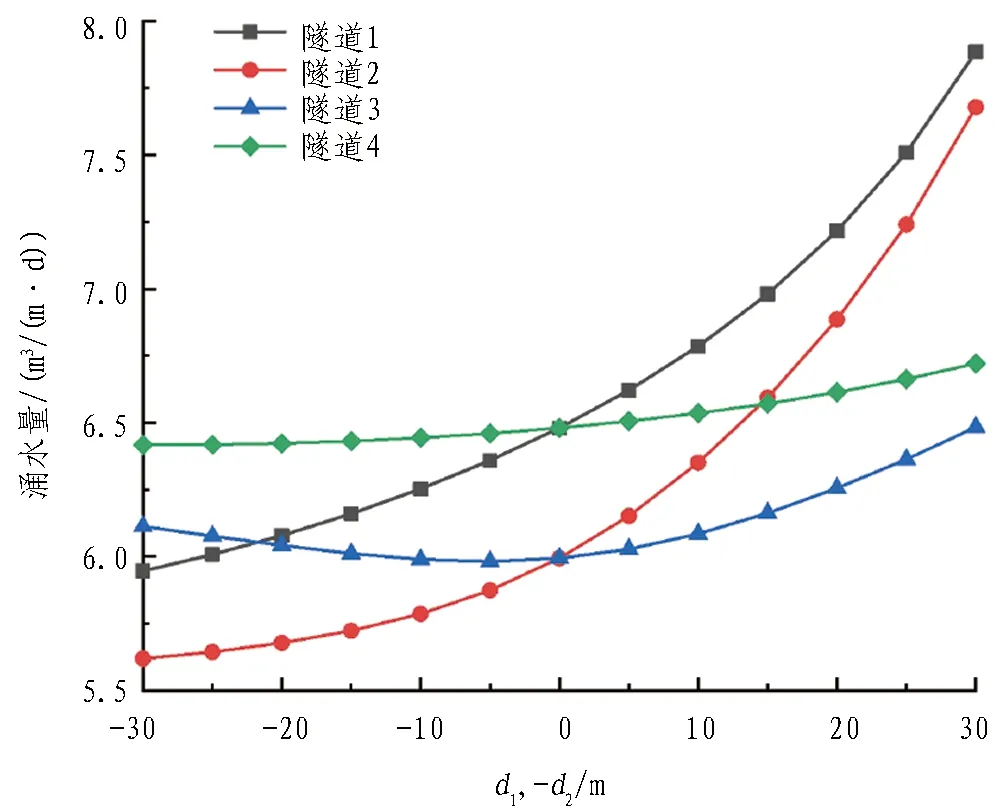
(c) d1与d2同时变化(工况3)图6 隧道涌水量与竖向间距的关系Fig. 6 Relationship between water inflow and vertical spacing in tunnel

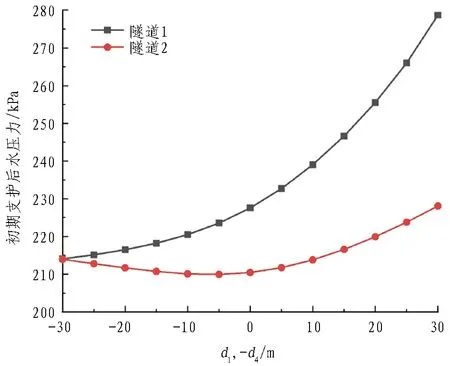
(a) d1与d4同时变化(工况1)

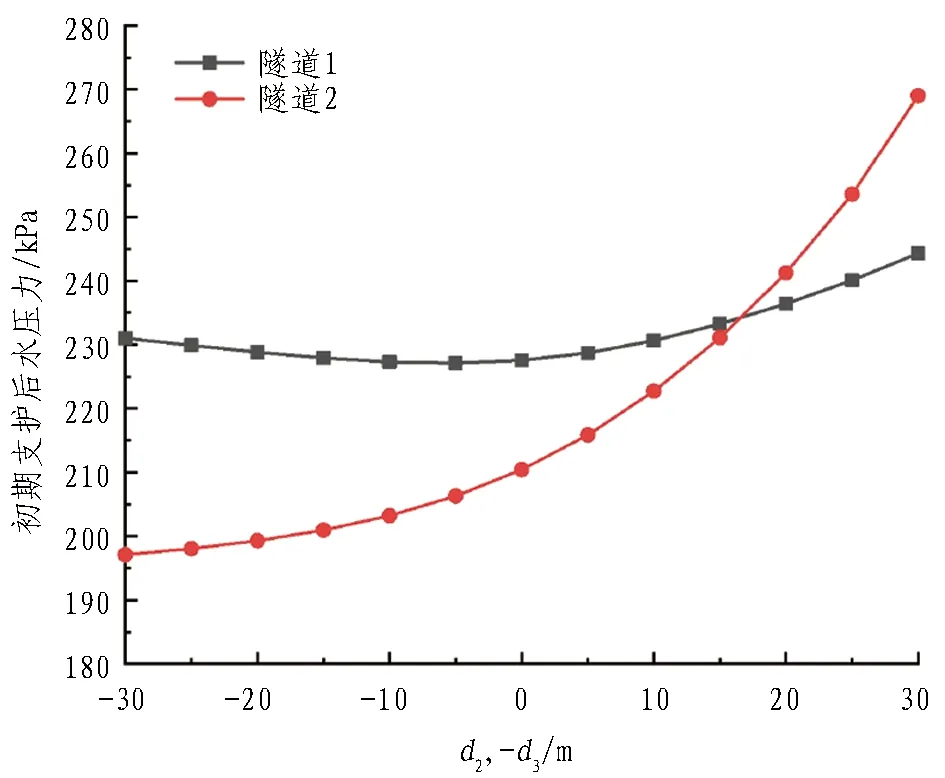
(b) d2与d3同时变化(工况2)

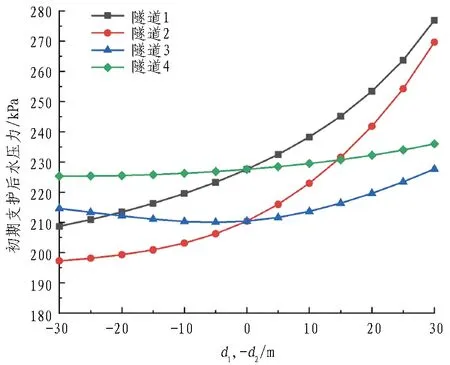
(c) d1与d2同时变化(工况3)图7 初期支护后水压力与竖向间距的关系Fig. 7 Relationship between water pressure and vertical spacing after primary supporting

3.2 隧道相对大小的影响

通过对目前已有工程的调研，大多数平行4孔山岭隧道均采用对称的布置形式，即位于外侧的2个隧道大小相同，位于内侧的2个隧道大小相同，本节也采用相同的布置形式，设置隧道1与隧道4半径相同，隧道2与隧道3半径相同，设隧道1与隧道2的半径比为n1，隧道2与隧道1的半径比为n2。同时本节设置了2种工况来研究隧道相对尺寸对隧道涌水量及初期支护后水压力的影响规律。1)工况1，保持隧道2、3的半径不变，改变n1的大小； 2)工况2，保持隧道1、4的半径不变，改变n2的大小。图8与图9分别给出了隧道1与隧道2涌水量及初期支护后水压力随半径比变化的结果。从图8—9中可以看出： 1)相同埋深与支护条件下，随着隧道半径的增大，隧道涌水量逐渐增大，同时，半径不变的隧道涌水量随之逐渐减小。2)当隧道半径相同时，外侧隧道涌水量及初期支护后水压力大于内侧隧道；当外侧隧道半径较大时，半径较大的隧道涌水量较大，且初期支护后水压力较大；当外侧隧道半径较小时，半径较大的隧道涌水量较大但初期支护后水压力较小。3)通过计算隧道1与隧道2涌水量的和可以看出，当半径比小于1时，工况1的总涌水量要小于工况2;当半径比大于1时，工况1的总涌水量则要大于工况2;当半径比为0.5时，工况1(小半径隧道位于外侧)总涌水量为工况2(小半径隧道位于内侧)总涌水量的96%；当半径比为1.5时，工况2(小半径隧道位于外侧)总涌水量为工况1(小半径隧道位于内侧)总涌水量的97.6%。故对4孔隧道来说，小半径隧道布置于外侧，大半径隧道布置于内侧时，总渗水量比较小。

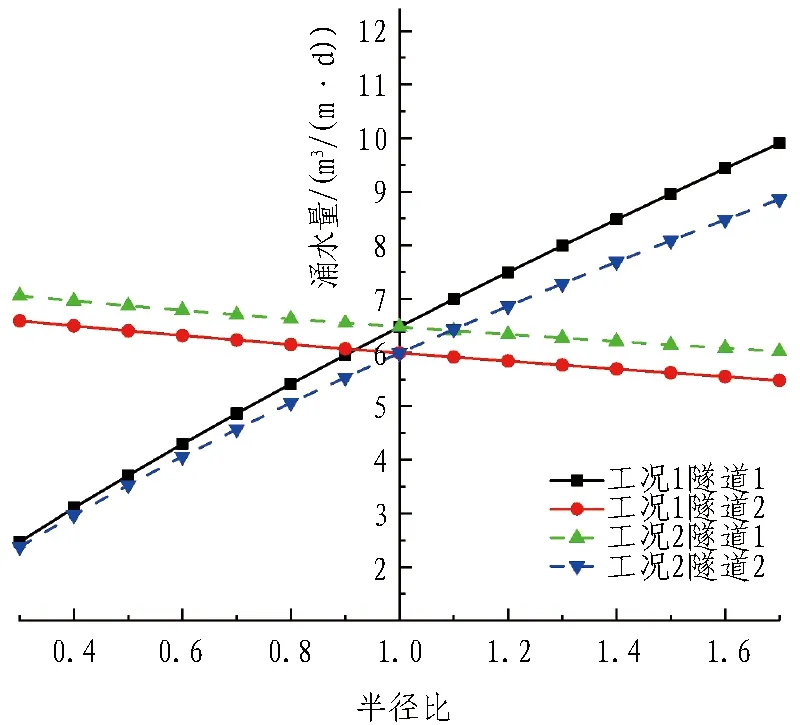
图8 隧道涌水量与隧道相对大小的关系Fig. 8 Relationship between water inflow and tunnel relative dimension

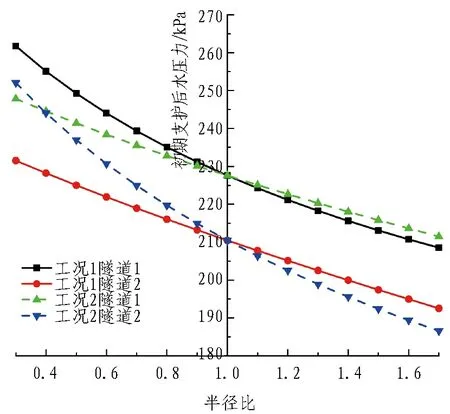
图9 初期支护后水压力与隧道相对大小的关系Fig. 9 Relationship between water pressure after primary supporting and tunnel relative dimension

3.3 初期支护参数的影响

设围岩与初期支护的渗透系数之比为n3，且围岩渗透系数保持不变，隧道涌水量、初期支护后水压力与初期支护厚度及渗透系数的关系如图10和图11所示。图中工况1、2、3分别代表初期支护厚度为0.5、1、1.5 m时的情况。

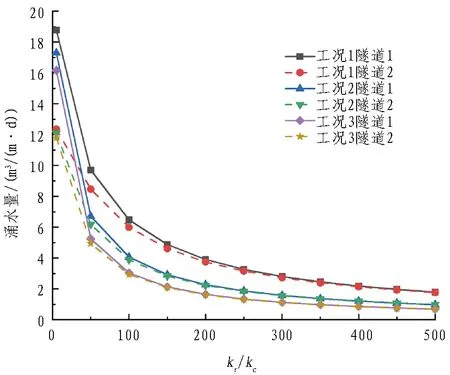
图10 隧道涌水量与初期支护参数的关系Fig. 10 Relationship between tunnel water inflow and primary support parameters

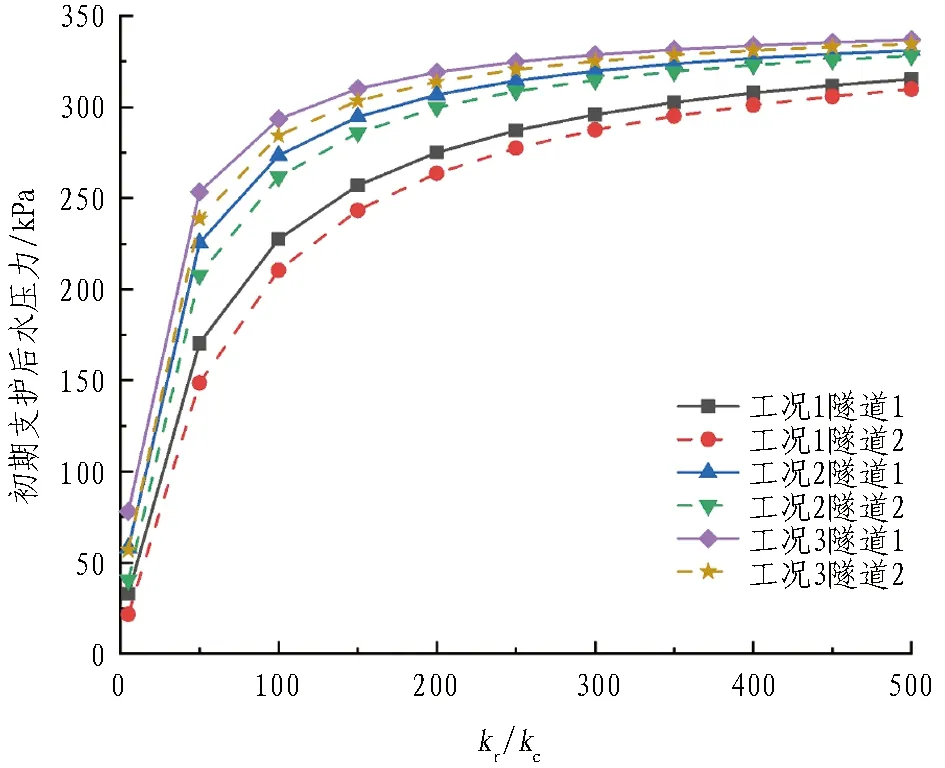
图11 初期支护后水压力与初期支护参数的关系Fig. 11 Relationship between water pressure after primary supporting and primary support

从图10和图11中可以看出： 1)随着初期支护厚度的增大、渗透系数的减小，隧道涌水量逐渐减小，初期支护后水压力则逐渐增大。2)当n3<100时，随着n3的增大，隧道涌水量与初期支护后水压力均变化迅速，且初期支护厚度越大，变化越迅速；当n3>100时，涌水量与初期支护后水压力随n3的变化幅度较为平缓，且不同支护厚度条件下变化幅度相近，说明当n3<100时支护厚度的改变对多孔隧道渗流场影响较大，而当n3>100时，则影响不明显。3)隧道涌水量和初期支护后水压力与初期支护厚度为非线性相关，如隧道1，当n3=100时，初期支护厚度从0.5 m增加到1 m，隧道涌水量下降37.1%，初期支护后水压力增加20.2%； 而当初期支护厚度从1 m增加到1.5 m时，隧道涌水量仅下降25.4%，初期支护后水压力增加7.3%。4)随着n3的逐渐增大，隧道1与隧道2的涌水量以及初期支护后水压力逐渐接近，隧道间的相互作用逐渐减弱，并且在相同n3条件下，初期支护厚度越大，隧道间作用减弱越明显。

4 结论与讨论

1)本文建立了平行4孔隧道渗流场的计算模型，以镜像法与渗流理论为基础给出了该问题的解答，通过与前人研究及数值模拟的对比，验证了本文所推导解析解的正确性，并分析了隧道参数和初期支护参数对隧道涌水量及初期支护后水压力的影响规律。

2)平行多孔隧道渗流场中隧道间的相互影响更大程度体现在相邻隧道间，主要影响距离为20倍隧道半径，并且随距离的增加影响逐渐减弱；同侧多孔隧道间距变化带来的影响要显著于异侧同等条件变化所带来的影响。

3)当平行4孔隧道为对称布置形式时，隧道间竖向间距接近1倍隧道半径时，埋深较深的隧道涌水量及初期支护后水压力最小，并随隧道间距的增大而增大。

4)在埋深及支护条件不变的情况下，增大隧道的半径，该隧道涌水量增大，其余隧道涌水量减小；小半径隧道置于外侧、大半径隧道置于内侧的布置形式有利于控制平行4孔隧道的总涌水量。

5)随着初期支护渗透系数的减小及其厚度的增大，隧道涌水量逐渐减小，初期支护后水压力逐渐增大，隧道间相互影响逐渐减弱；初期支护渗透系数与其厚度和隧道涌水量及支护后水压力均为非线性关系，在施工中应协调两者关系，以便经济有效地控制隧道排水量及初期支护受力情况。

利用本文所推导的解析解重点针对隧道涌水量及初期支护后水压力进行了分析，但对于具体某点的水头及其分布情况研究较少，而且在假设中对于衬砌防排水性能的考虑较为理想，后续可在本文解析解基础上进一步研究。同时，本文仅研究了不同工程参数对平行4孔隧道渗流场的影响，后续可深入研究各参数的影响程度，为类似工程防排水方案制定提供参考。