基于WOA-DELM的成都地铁建设阶段温室气体预测

陈 政， 郭亚林， 郭 春

(西南交通大学 交通隧道工程教育部重点实验室， 四川 成都 610031)

0 引言

随着国家碳排放战略布局的进行，绿色工程逐渐成为设计研究重点。地铁工程由于方便快捷，逐渐成为城市建设的热点。截至2020年，成都地铁总长超500 km。预计到2025年底，成都市修建和运营地铁里程将达到850 km，远期规划36条线路，总长约1 666 km[1]。由于地铁建设工程量逐渐增大，其碳排放控制已成为绿色工程建设的重要组成部分。

目前，国内外已对轨道交通建设期的碳排放展开了相关研究。Morita等[2]建立了城市轨道交通建设期的碳排放模型； 文献[3]采用GHGProtocol研究了伦敦地下结构建设期的碳排放足迹； Chang等[4-5]采用生命周期方法对加利福尼亚高速铁路建设阶段的碳排放进行了测算，发现建材生产碳排放约占总排放量的80%，而建材运输约占15%； 郜新军[6]从生命周期角度评估了轨道交通系统建设期和运营期的碳排放，得到碳排放最高阶段为运营期，其次是建设期； Liu等[7]采用生命周期评价方法对明挖地铁和暗挖地铁建设期碳排放量进行对比，得到暗挖地铁每m2碳排放量较大； Liu等[8]采用基于定额的方法对北京明挖地铁建设期间碳排放量进行计算，得到主体结构在建设过程中碳排放量约占总排放量的69%，总体碳排放中混凝土和钢材碳排放占比最大。

在地铁车站和区间碳排放计量方面，粟月欢等[9]采用全生命周期评价法对深圳地铁碳排放量进行计算，得到地铁建设阶段盾构区间碳排放量为1.3万tCO2e/km，地铁车站碳排放量约为3.71 tCO2e/m2； Liu等[10]采用人工神经网络对福州地铁设计阶段的碳排放量进行预测，得到福州地铁碳排放量为5.3万tCO2e/km，并建立了埋深与地铁车站和盾构区间碳排放量的关系式； 王幼松等[11]、黄旭辉[12]对广州地铁物化阶段碳排放量进行研究，得到广州地铁车站物化阶段碳排放量为6.057 tCO2e/m2，盾构区间物化阶段碳排放量为13.264 tCO2e/m； Li等[13]通过全生命周期评价方法对上海地铁碳排放量进行计算，得到建设阶段上海地铁车站和区间碳排放总量为2 681 427.99 tCO2e，建设阶段碳排放量相当于地铁运营28年的碳排放量； 贺晓彤[14]对北京某地铁车站碳排放量进行全生命周期评价，得到该地铁车站平均每建筑平米碳排放量约为4.81 tCO2e，同时研究得到单柱双跨地铁车站碳排放量随埋深线性增加，增量为743.05 tCO2e/m。

在预测碳排放方法上，有学者采用了智能机器学习算法[15-22]，如人工神经网络。但智能机器学习算法对于数据非常敏感[23]。目前，深度极限学习机在碳排放预测方面应用较少，因此有必要采用不同算法进行对比分析，以选取合适模型对地铁碳排放进行预测分析。

由于基于生命周期的碳排放存在较强的地域依赖性，且关于成都地铁建设阶段碳排放的研究很少，因此有必要研究成都地铁建设阶段的碳排放情况。本文基于生命周期评价(life cycle assessment，LCA)框架对成都地铁建设阶段的碳排放进行计算，利用WOA-DELM算法建立成都地铁碳排放预测模型，并对主要输入指标进行敏感性分析，利用得到的碳排放影响高敏感性指标拟合成都地铁碳排放粗略预测公式。

1 地铁碳排放计算方法及预测模型基本原理

1.1 碳排放研究范围

结合LCA碳排放评价框架，根据建设阶段碳排放的来源[24]和现有地铁碳排放相关文献[9-10]，将地铁碳排放研究的时间范围限定为地铁的建设阶段，将地铁碳排放来源分为： 1)建筑材料生产产生的碳排放； 2)建筑材料运输产生的碳排放； 3)现场施工机械能耗产生的碳排放。地铁碳排放系统边界如图1所示。

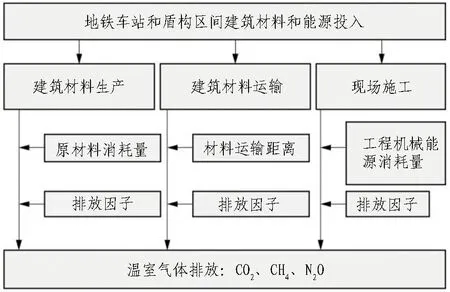
图1 地铁碳排放系统边界Fig. 1 Boundary of metro carbon emission system

碳排放量采用等效二氧化碳的方法衡量，计算公式为

CO2eqi=Mi×GWPi。

(1)

式中：Mi为第i种温室气体质量，本文研究的温室气体类型为CO2、CH4和N2O； GWPi为全球变暖潜势值，根据联合国政府间气候变化专门委员会(IPCC)提出的《2021年气候变化： 物理科学基础》，选用的温室气体100年基准期全球变暖潜势值如表1所示。

表1 温室气体100年基准期全球变暖潜势值Table 1 Global warming potential of greenhouse gases in 100-year base period

1.2 碳排放计算方法

本文选用碳排放系数法对地铁碳排放进行计算，计算公式为

Ctotal=Cm+Ct+Co。

(2)

Cm=∑Mmat,iFmat,i。

(3)

Ct=∑Mtrans,iLtrans,iFtrans,i。

(4)

Co=∑Mmach,iFmach,i。

(5)

式(2)—(5)中：Ctotal为碳排放总量，kgCO2e；Cm为建筑材料生产碳排放总量，kgCO2e；Ct为建筑材料运输碳排放总量，kgCO2e；Co为场内施工能耗碳排放总量，kgCO2e；Mmat,i为第i种建筑材料消耗量，kg；Fmat,i为第i种建筑材料生产碳排放因子，kgCO2e/kg；Mtrans,i为第i种建筑材料运输机械能源消耗量，kg；Ltrans,i为第i种建筑材料运输机械运输距离，km；Ftrans,i为第i种建筑材料运输机械碳排放因子，kgCO2e/(kg·km)；Mmach,i为第i种场内施工机械能源消耗量，kg；Fmach,i为第i种场内施工机械能源生产和使用的碳排放因子，kgCO2e/kg。

1.3 预测模型和优化算法基本原理

1.3.1 模型输入指标的选择

地铁碳排放预测模型输入指标的选择代表着地铁结构工程量，从而影响地铁碳排放的预测。地铁碳排放预测模型输入指标的选择需要满足独立性和稳定性要求，能够全面反映地铁整体情况。根据Liu等[10]对地铁输入指标的研究，本文选取的地铁车站碳排放预测模型输入指标为地铁开挖方法、车站长度、车站宽度、车站高度、轨面埋深、总建筑面积、楼层数以及岛式站台宽度，地铁盾构区间碳排放预测模型输入指标为盾构面积、管片厚度、盾构区间长度和轨面平均埋深。

1.3.2 预测模型

1.3.2.1 BP (back propagation neural nctwork)基本原理

BP神经网络算法[25]是一种基于输出误差逆向传播的多层前馈神经网络算法，对于3层前馈神经网络，其基本结构由输入层、隐含层和输出层构成，每层的神经元个数分别为n、m、k，根据神经网络层建立的输出函数O以及误差函数E分别为

θk′] 。

(6)

(7)

式(6)—(7)中：ψ(x)和φ(x)分别为输出层和隐含层的传递函数；wjk、wik为连接权值的阈值；θj和θk′分别为隐含层和输出层的阈值；Oi为拟合预测输出值；xi和yi分别为隐含层输入和输出值；Ti和S分别为试验测试值和样本数量。

1.3.2.2 ELM(extreme learning machine)基本原理

ELM[26]是单隐层前向型网络，其基本表达式为

(8)

式中：βi为连接隐含层与输出层的输出权值；yi为网络输出值；gi(ωi·xj+bi)为第i个隐含层节点的激活函数；ωi为连接第i个隐含层节点和输入节点之间的权重；bi为网络第i个隐含层的偏置；K为隐藏节点；N为训练样本个数；xj=[xj1,xj2, …，xjn]T∈Rn为输入数据。

当激活函数逼近目标输出值时，tj=[tj1,tj2,…，tjn]T∈Rn，即

(9)

采用矩阵方式表示为

T=Hβ。

(10)

(11)

式(10)—(11)中：H为极限学习机隐含层输出矩阵；T为期望输出向量;β为输出权值矩阵。最终模型转换成β权值的求解。

1.3.2.3 KELM(kernel extreme learning machine)基本原理

KELM是将核函数引入ELM中得到[26]，其模型输出为

(12)

(13)

Ωi,j=h(xi)·h(xj)=K(xi,xj) 。

(14)

式(12)—(14)中：x为输入数据；β为KELM模型输出权值；h(x)为隐含层节点输出函数；Ωi,j为核矩阵；K(xi,xj)为核函数，本文选用RBF核函数；I为对角矩阵；C为惩罚系数，本文取2；T为期望输出向量。

1.3.2.4 DELM基本原理

DELM是多个ELM-AE(extreme learning machine autoencoder)堆叠而成的深度学习网络[27]，基于ELM、DELM权值表示为

(15)

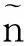
本文选用Sigmoid激活函数，隐含层取2层，每层节点分别为2个和3个。优化迭代计算中，种群数量取20，最大迭代次数取50，权值上下边界为[-1,1]。

1.3.3 优化算法基本原理

1.3.3.1 WOA优化算法基本原理

WOA优化算法[28]是一种模仿座头鲸捕猎行为的优化算法。鲸鱼在捕猎过程中会制造气泡网包围自己的身体，在搜索过程中，鲸鱼彼此远离，以确保更高的捕猎效率。其迭代公式为

Xt+1=Xrand-A|CXrand-Xt| 。

(16)

A=2ar-a。

(17)

C=2r。

(18)

式(16)—(18)中：Xt是鲸鱼位置向量；Xrand由当前鲸鱼的位置确定； 随着迭代进行，向量a从2到0线性减小，向量r在0到1之间随机变动；C为由向量r确定的系数矩阵;A为由a决定的系数矩阵。

开始迭代时，由于a向量值较大，|A|值将大于1，从而保证寻求最优解的可靠范围； 当|A|值小于1时，包围猎物的过程开始，此时计算公式为

(19)

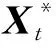
1.3.3.2 WDO优化算法基本原理

WDO优化算法[29]来源于风的运动可以自动补偿大气压力的不平衡原理，以空气单元速度和位置进行迭代求最优解。空气单元位置和速度迭代公式为

(20)

xnew=xcur+unewΔt。

(21)

c=-2|Ω|RT。

(22)

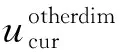
1.3.3.3 GWO优化算法基本原理

GWO优化算法[30]模拟自然界灰狼狩猎方法，每个狼都代表一个候选解答。通过模拟灰狼群等级制度，该算法将狼群分为α、β、δ、ω4个等级。前3个等级中的狼代表了当前最优解。GWO模型中第1步为包围猎物，公式为

X(t+1)=Xp(t)-A|CXp(t)-X(t)| 。

(23)

A=2ar1-a。

(24)

C=2r2。

(25)

式(23)—(25)中：X(t)和Xp(t)分别为灰狼和猎物的位置向量；t为当前迭代次数； 随着迭代进行，a向量从2到0线性减小，r1和r2向量在0到1之间随机变动;A为向量a和r1决定的系数矩阵；C为由向量r2决定的系统矩阵。

在GWO算法中有一种特殊机制，假定α、β、δ等级中的狼可以获得更多猎物的潜在信息，ω等级中的狼必须跟随α、β、δ等级中的狼，以更新其位置来更靠近猎物，公式为

(26)

X1=Xα-A1|C1Xα(t)-X(t)| 。

(27)

X2=Xβ-A2|C2Xβ(t)-X(t)| 。

(28)

X3=Xδ-A3|C3Xδ(t)-X(t)| 。

(29)

1.3.3.4 PSO优化算法基本原理

PSO优化算法[28]模拟了生物种群的协作行为，即特征空间中的每个粒子都拥有一个适应度值，粒子间可以相互协调以达到最优适应度，公式为

Xt+1=Xt+Vt+1。

(30)

Vt+1=wVt+c1r1(Pt-Xt)+c2r2(Pg,t-Xt) 。

(31)

式(30)—(31)中：t为迭代次数；Xt为粒子位置向量；Vt为粒子速度向量；w为惯性权重；c1、c2为认知和社交尺度参数；r1、r2为均匀分布随机变量；Pt为粒子个体最优位置向量；Pg，t是粒子群最优位置向量。

1.3.3.5 ABC优化算法基本原理

ABC优化算法[31]模拟蜂群采蜜过程，包含生成初始蜜源(式(32))、采蜜蜂选择蜜源(式(33))、观察蜂尝试蜜源(式(34))。如果没有合适的蜜源，采蜜蜂将重新选择蜜源，直到寻找到最佳蜜源，即迭代求到最优解。

xij=Xmin+rand(0,1)(Xmax-Xmin) 。

(32)

xij′=xij+rij(xij-xkj),k≠i。

(33)

(34)

式(32)—(34)中:i∈{1,2,…,N}(N为蜜源个数)，j∈{1,2,…,D}(D为采蜜蜂选择蜜源个数)；Xmin和Xmax是初始区域蜜源上下边界；xij为Xi区域内的第j个蜜源，Xi=[x11,x12,…,xij]；xij′为寻找的新蜜源；rij为[-1,1]中的随机数；k为蜜源随机位置；pi为最优蜜源概率； fiti为蜜源适应度值。

1.3.3.6 MVO优化算法基本原理

MVO优化算法[30]基于宇宙膨胀和宇宙间物质交换，同时引入黑洞、白洞和虫洞概念，对最优宇宙进行筛选，其基本公式包括多元宇宙的生成(式(35))、宇宙间物质的更新(式(36))、虫洞对宇宙物质的转移(式(37))。

(35)

(36)

(37)

(38)

(39)

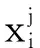
1.3.3.7 ASO优化算法基本原理

ASO优化算法[32]是基于原子物理运动规律建立的模型，根据单个原子在作用力和约束力作用下产生的加速度对其位置和速度进行最优筛选，第i个原子迭代公式为

(40)

(41)

1.4 模型性能指标及评价函数

根据相关文献研究[28, 33-35]，选取预测模型的性能指标为均方根误差(root mean square error, RMSE)、平均百分比误差(mean absolute percentage error, MAPE)、平均绝对误差(mean absolute error, MAE)、决定系数(coefficient of determination,R2)、一致性指数(index of agreement, IA)，将通过训练和测试结果一致性指数乘积最大者所对应的拟合数据作为单个模型最优值。为对比各模型的优劣性能，选用一致相关性概率PRIA作为评价模型优劣的函数。

(42)

(43)

(44)

(45)

(46)

(47)

(48)

PRIA=PR·PIA。

(49)

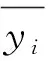
2 地铁碳排放数据清单分析

2.1 工程概况

本文工程量清单数据为成都地铁18号线6车站和7区间施工概算工程量清单数据(2018年)，选用的地铁车站均为明挖法施工，区间均为盾构法施工，将选用的模型输入指标作为模型主要因素，地铁车站和盾构区间工程概况分别如表2和表3所示。

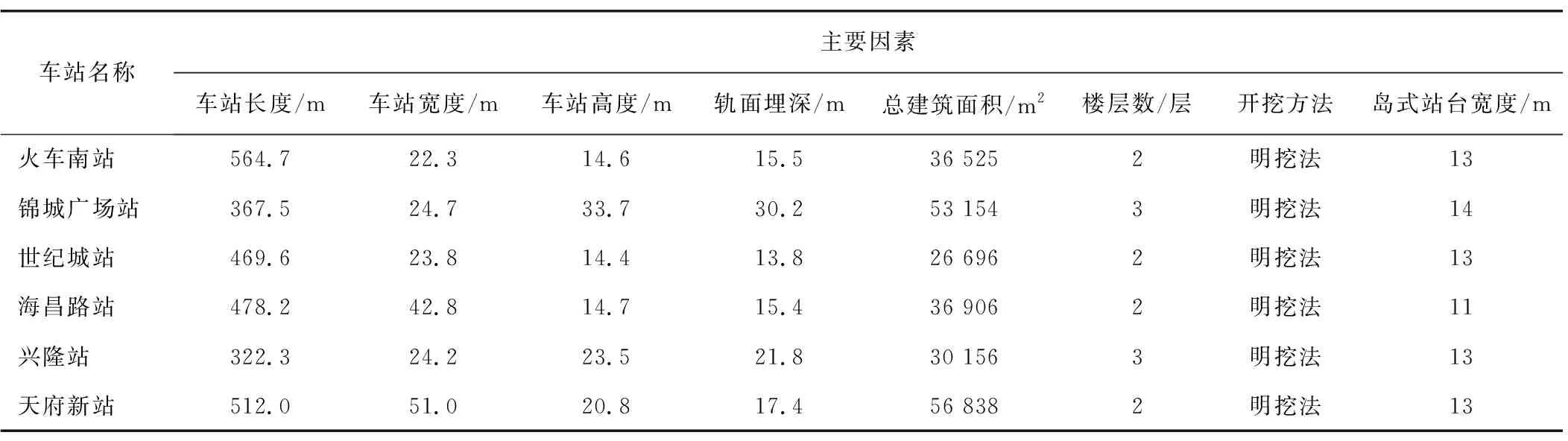
表2 地铁车站工程概况Table 2 Overview of metro station projects

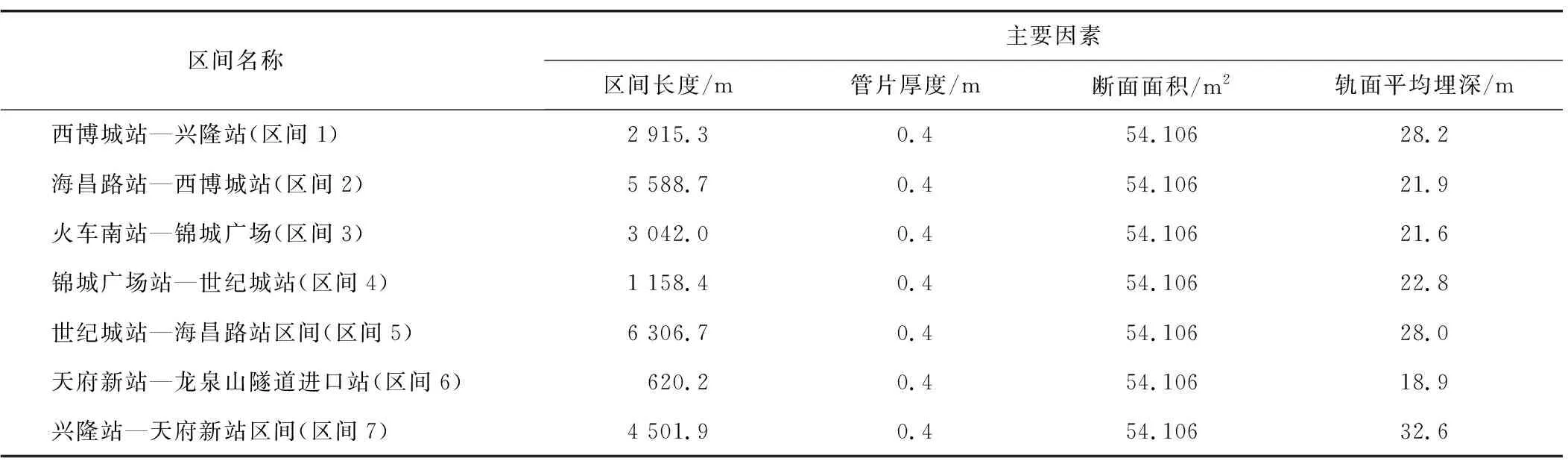
表3 地铁盾构区间工程概况Table 3 Overview of metro shield section projects

2.2 碳排放因子

所选用碳排放因子来源于GB/T 51366—2019《建筑碳排放计算标准》、《2017—2019年度中国区域电网基准线排放因子》及相关文献[8-9, 11-14, 36-40]，如表4所示。

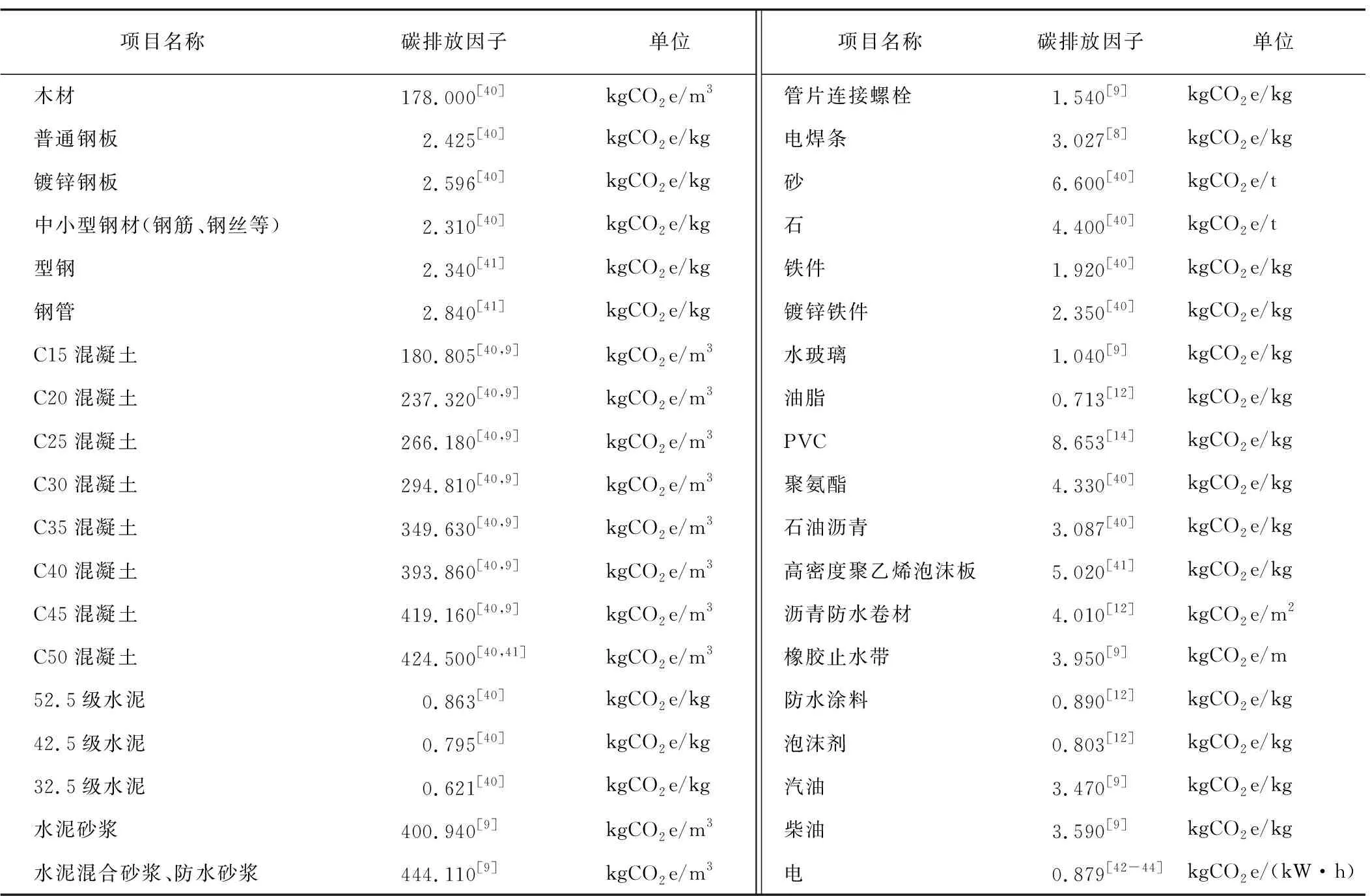
表4 材料碳排放因子Table 4 Carbon emission factors

2.3 地铁碳排放计算

根据碳排放计算原理，对各地铁车站及盾构区间碳排放总量进行计算，通过计算得到地铁车站和盾构区间碳排放较大的材料为水泥、混凝土和钢材。根据碳排放占比大小顺序，对于地铁车站另外选择了电焊条、防水卷材、石油沥青、铁制品、砂浆和木材作为碳排放计算数据； 对于盾构区间另外选择了电焊条、管片连接螺栓、风管、泡沫剂、止水带、铁制品和砂作为碳排放计算数据。建筑材料清单中忽略了其余碳排放占比累计值在1%以下的材料。

2.3.1 地铁建筑材料生产阶段碳排放

根据碳排放计算公式(3)，结合选用的地铁车站建筑材料用量和相应碳排放因子，计算得到地铁车站和地铁盾构区间建筑材料生产阶段碳排放量，分别如图2和图3所示。

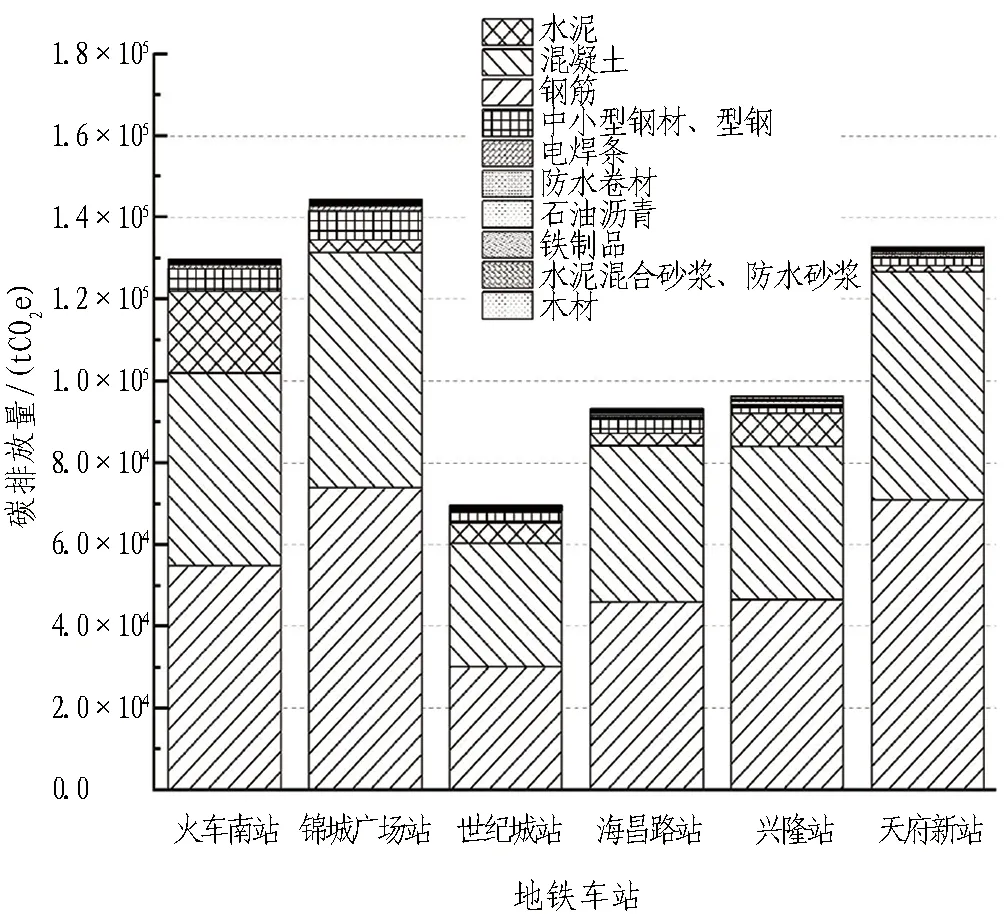
图2 地铁车站建筑材料生产阶段碳排放堆叠柱状图Fig. 2 Stacking histograms of metro station building materials carbon emission during production

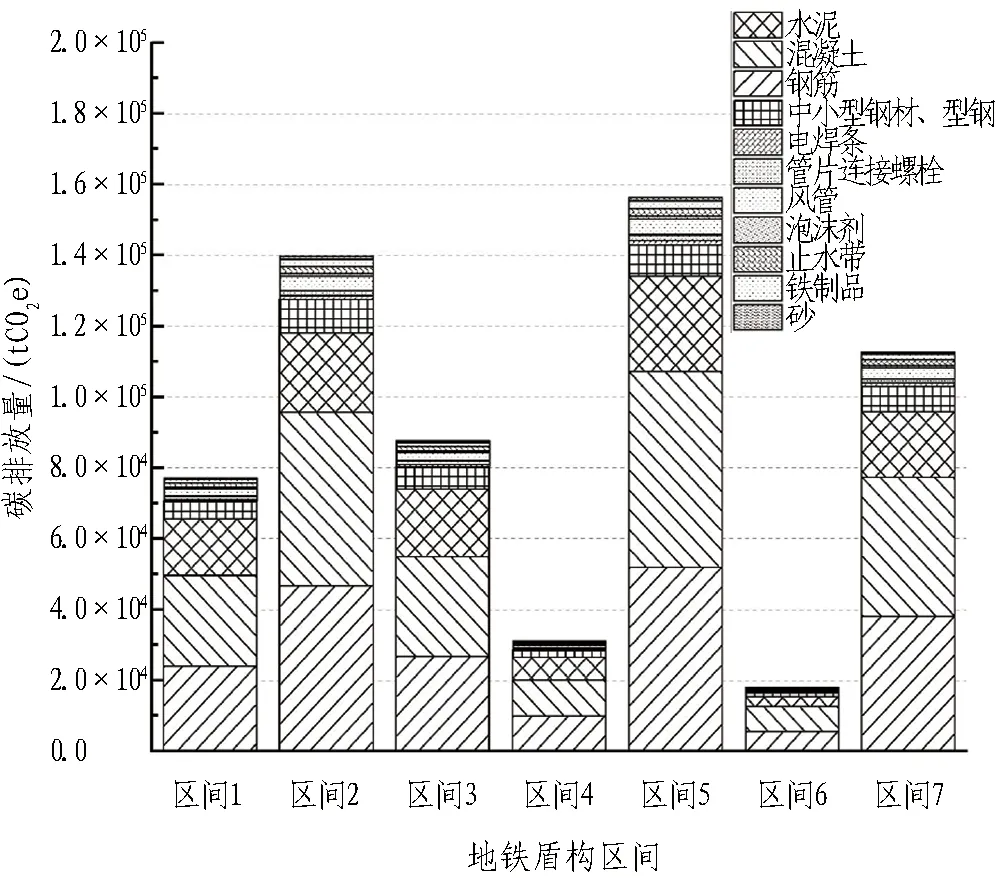
图3 地铁盾构区间建筑材料生产阶段碳排放堆叠柱状图Fig. 3 Stacking histograms of metro shield section building materials carbon emission during production

在建筑材料生产阶段，6个地铁车站碳排放总量平均值约为11.1万tCO2e。地铁车站碳排放较大的材料为钢筋，混凝土，水泥和中小型钢材、型钢。其中，钢筋碳排放在建筑材料生产阶段占比最大，平均占比45%左右； 其次是混凝土，平均占比40%左右；水泥和中小型钢材、型钢碳排放之和占比平均值约10%。

在建筑材料生产阶段，7个地铁盾构区间碳排放总量平均值约为8.9万tCO2e。其中，碳排放占比较大的材料为钢筋和混凝土，两者占比均为33%左右； 其次为水泥，约占20%； 中小型钢材、型钢占比为7%左右； 其他材料中风管碳排放占比接近3%，管片连接螺栓、止水带、铁制品碳排放占比总和为1%左右。

地铁车站和盾构区间碳排放较大的材料均为钢筋，混凝土，水泥和中小型钢材、型钢，盾构区间其他材料碳排放占比是地铁车站其他材料碳排放占比的3倍多。

2.3.2 地铁建筑材料运输阶段碳排放

假定地铁建筑材料采用中型柴油货车运输，同时假定成都地铁建筑材料均为同城运输，运距均取为20 km。根据GB/T 51366—2019《建筑碳排放计算标准》，运输碳排放因子取为0.18 kgCO2e/(t·km)。根据式(4)，计算各地铁车站和盾构区间建筑材料运输阶段碳排放，结果分别如图4和图5所示。

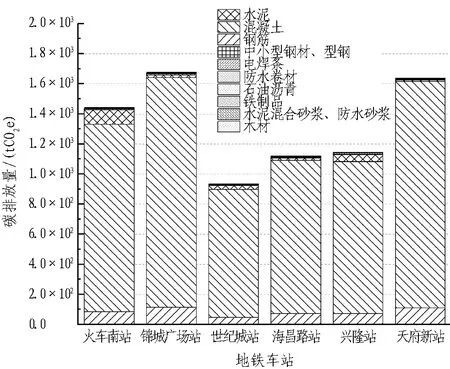
图4 地铁车站建筑材料运输阶段碳排放堆叠柱状图Fig. 4 Stacking histograms of metro station building materials carbon emission during transportation

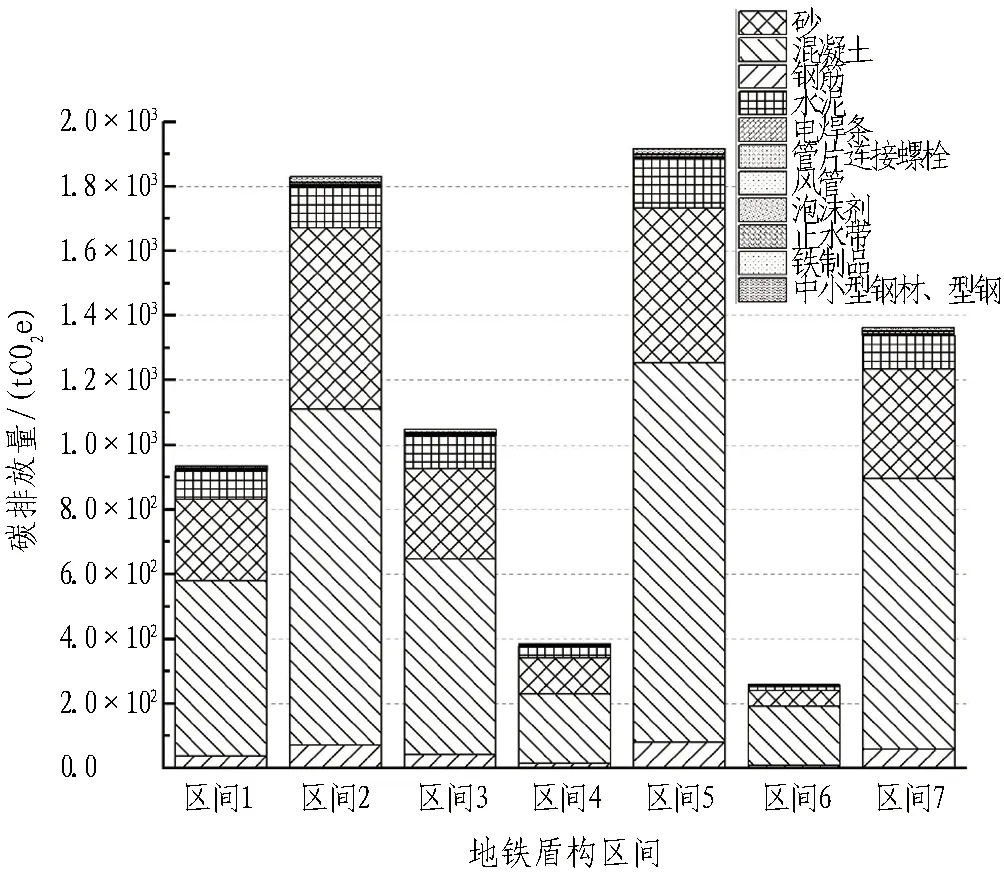
图5 地铁盾构区间建筑材料运输阶段碳排放堆叠柱状图Fig. 5 Stacking histograms of metro shield section building materials carbon emission during transportation

通过计算得到，在建筑材料运输阶段，6个地铁车站碳排放平均值为1 326.772 tCO2e，7个盾构区间碳排放平均值为1 105.909 tCO2e。在建筑材料运输阶段，地铁车站碳排放占比最大的材料为混凝土，占比均值约为90%； 其次是钢筋，占比均值约为6%。盾构区间建筑材料运输阶段碳排放占比较高的材料同样为混凝土，占比均值约为60%； 其次为砂，占比均值约为25%； 钢筋和水泥碳排放占比总和约为10%。在建筑材料运输阶段，地铁车站和盾构区间碳排放量均值大致相等。

2.3.3 地铁施工阶段碳排放

地铁施工阶段碳排放包含场内运输机械、工程机械以及临时生活照明消耗的能源碳排放。根据式(5)，计算各地铁车站和盾构区间施工阶段碳排放，结果分别如图6和图7所示。在施工阶段，6个地铁车站碳排放平均值为1.033万tCO2e，7个盾构区间碳排放平均值为1.816万tCO2e。地铁车站施工阶段碳排放占比最大的能源为柴油，占比均值约为80%，是电能耗碳排放均值的5倍左右；盾构区间施工阶段碳排放占比最大的能源为电，占比均值约为65%，是柴油能耗碳排放均值的2倍左右。

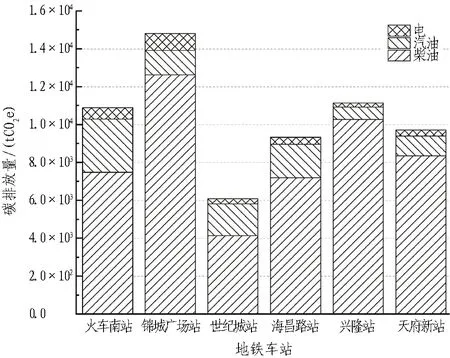
图6 地铁车站施工阶段碳排放堆叠柱状图Fig. 6 Stacking histograms of metro station building materials carbon emission during construction

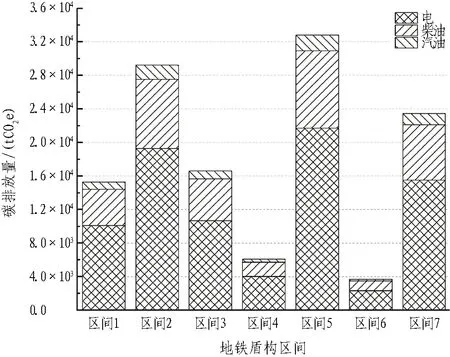
图7 地铁盾构区间施工阶段碳排放堆叠柱状图Fig. 7 Stacking histograms of metro shield section building materials carbon emission during construction

2.4 预测模型建立

模型训练和测试样本均取为50%样本总量，在训练和测试过程中随机选取样本，模型随机训练预测总次数取为1 000次。根据地铁车站和盾构区间输入指标，结合不同车站和盾构区间碳排放计算量，建立DELM输入和输出基本模型，同时按照WOA优化算法对每次训练的DELM权值参数进行优化，筛选更优的预测结果，最终将得到的最优权值赋予DELM，得到相应地铁车站和盾构区间的预测模型。具体的模型建立流程如图8所示。由于样本地铁车站开挖方法均为明挖法，且盾构区间面积、管片厚度均为定值，本文最终得到的WOA-DELM地铁车站碳排放预测模型仅适用于采用明挖法开挖的地铁车站碳排放预测，WOA-DELM盾构区间碳排放预测模型仅适用盾构面积为54.106 m2(盾构直径8.5 m)、管片厚度为0.4 m的盾构区间碳排放预测。

图8 地铁碳排放WOA-DELM预测模型建立流程图Fig. 8 Flowchart of metro carbon emissions based on WOA-DELM prediction model

3 结果分析

3.1 碳排放计算结果分析

地铁车站和盾构区间建设不同阶段碳排放量分别如图9和图10所示。6个地铁车站在不同建设阶段碳排放平均值占比如图11所示，7个盾构区间在不同建设阶段碳排放平均值占比如图12所示。计算得到案例选用的6个成都地铁车站每建筑平米碳排放平均值为3.12 tCO2e，7个盾构区间每公里碳排放平均值为3.242万tCO2e。

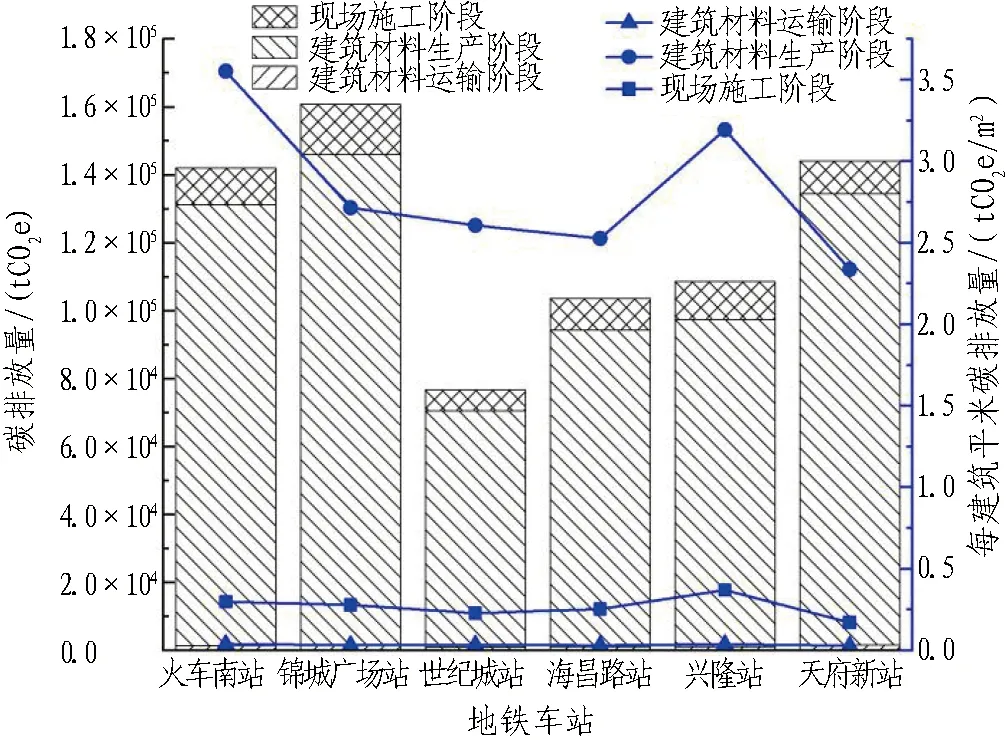
图9 地铁车站建设不同阶段碳排放堆叠柱状图Fig. 9 Stacking histograms of metro station carbon emission

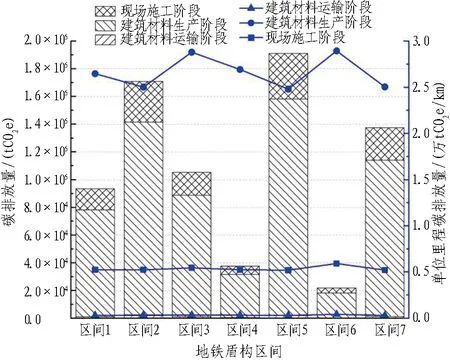
图10 地铁盾构区间建设不同阶段碳排放堆叠柱状图Fig. 10 Stacking histograms of metro shield section carbon emission

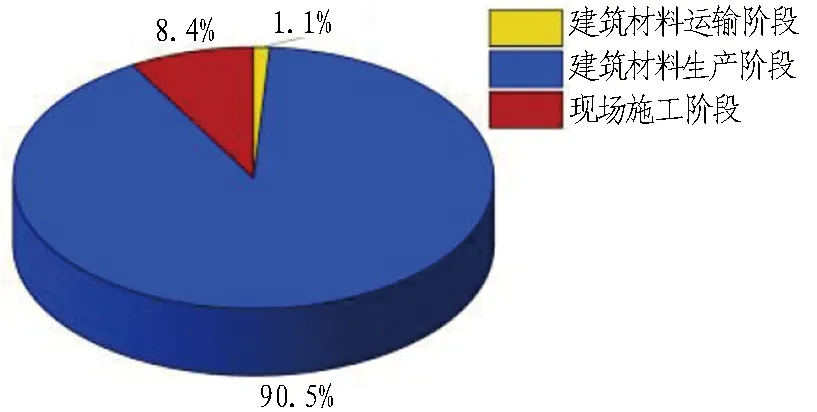
图11 6个地铁车站在不同建设阶段碳排放平均值占比饼图Fig. 11 Pie chart of carbon emissions during metro station construction

图12 7个盾构区间在不同建设阶段碳排放平均值占比饼图Fig. 12 Pie chart of carbon emissions during metro shield section construction

从图9和图11中可以看出： 1)地铁车站在建筑材料生产阶段碳排放最大，其次是现场施工阶段，最后是建筑材料运输阶段，碳排放占比依次为90.5%、8.4%和1.1%； 2)建筑材料生产所产生的碳排放量约是建筑材料运输和现场施工碳排放量总和的10倍。

从图10和图12中可以看出： 1)地铁盾构区间同样在建筑材料生产阶段碳排放最大，其次是现场施工阶段，最后是建筑材料运输阶段，碳排放占比依次为82.2%、16.8%和1%； 2)建筑材料生产所产生的碳排放量约是建筑材料运输和现场施工碳排放量总和的4.4倍。

从图11和图12中可以看出： 地铁盾构区间现场施工碳排放量占比是地铁车站现场施工碳排放量占比的2倍。其原因可能为盾构机械施工及其附属机械耗电量较大，导致盾构区间现场施工碳排放量较大。

从图9中可以看出： 1)在地铁车站建设阶段，碳排放最大的车站为锦城广场站，碳排放为16 万tCO2e左右，约为碳排放最小车站(世纪城站)的2倍； 2)在每建筑平米碳排放量折线图中，建筑材料生产阶段不同车站每建筑平米碳排放量波动较大，最大差值约为1 tCO2e/m2，现场施工和建筑材料运输阶段不同车站每建筑平米碳排放差别不大。

从图10中可以看出： 1)在地铁盾构区间建设阶段，碳排放最大的区间为世纪城站—海昌路站区间(区间5)，碳排放为19万tCO2e左右，约为碳排放最小区间天府新站—龙泉山隧道进口站(区间6)的9倍； 2)在单位里程碳排放量折线图中，建筑材料生产阶段不同盾构区间单位里程碳排放量最大差值为0.5万tCO2e/km，现场施工和建筑材料运输阶段不同盾构区间单位里程碳排放量相对稳定。

3.2 预测模型性能指标分析

通过模型计算，得到各模型一致性最优结果，各模型地铁车站预测结果性能指标与评价函数对比如图13所示。各模型地铁盾构区间预测结果性能指标与评价函数对比如图14所示。

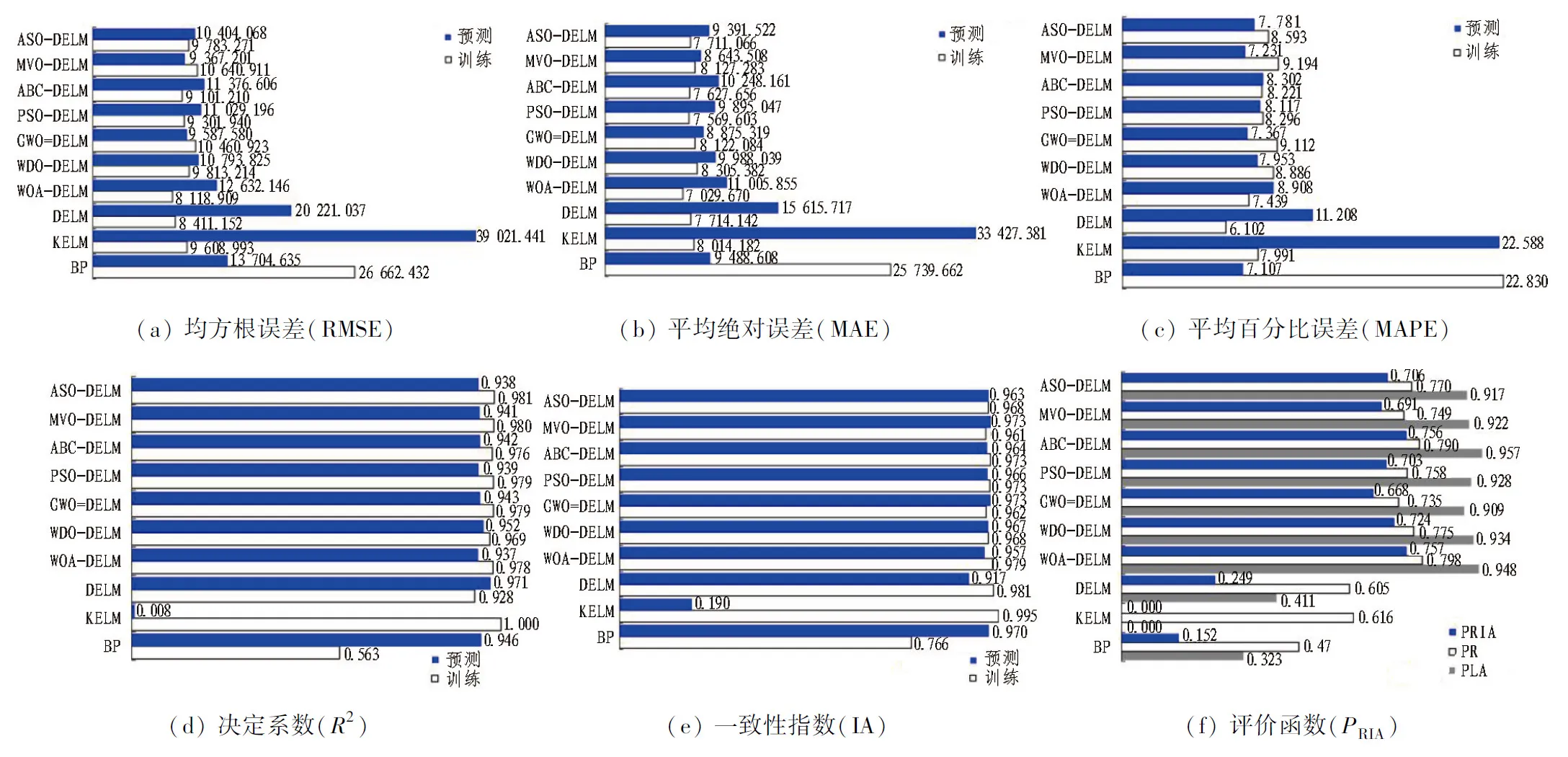
图13 各模型地铁车站预测结果性能指标与评价函数对比Fig. 13 Performance index and evaluation function of metro station prediction results

图14 各模型地铁盾构区间预测结果性能指标与评价函数对比Fig. 14 Performance index and evaluation function of metro shield section prediction results

从图13可以看出： 在保持训练和预测结果一致相关性指数IA最大时，各模型得到的训练数据结果决定系数略大于预测数据结果。KELM和BP模型的均方根误差(RSME)、平均绝对误差(MAE)和平均百分比误差(MAPE)均较大，且KELM预测决定系数为0，说明KELM和BP模型对于地铁车站低维数据的预测效果较差。DELM由于嵌套了多层编码器，构成了多层神经网络，可对数据进行降维和升维，保证数据信息的精炼和全面性，其误差相对KELM和BP模型较小，且优化后的DELM一致相关性较普通DELM预测结果提高了1倍左右。WOA-DELM模型的一致相关性概率PRIA最大，为0.757； ABC-DELM模型的一致相关性概率略小于WOA-DELM模型，为0.756。

由图14可知： 在地铁盾构区间碳排放预测模型中，模型KELM、BP和ASO-DELM的预测结果误差较大，是其他模型的3～10倍，一致相关性概率只有其他模型的一半。由于盾构区间输入指标少，DELM及其优化模型预测结果一致相关性概率大部分大于0.95。其中，WOA-DELM模型和ABC-DELM模型一致相关性概率分别为0.984和0.996。

综合对比地铁车站和盾构区间各模型预测结果性能指标可知，WOA-DELM模型综合预测能力较强。WOA-DELM模型在预测结果一致相关性概率最大时的地铁车站和盾构区间拟合迭代误差如图15所示。其中，选用的适应度值为预测误差归一化后的数值。从图15(a)中可以看出，地铁车站拟合预测过程中，当迭代次数大于20时，模型预测适应度值趋于稳定；从图15 (b)中可以看出，当迭代次数大于8时，地铁盾构区间预测适应度值趋于稳定。WOA-DELM模型在整体预测中迭代均趋于稳定，表明当前寻优有效。

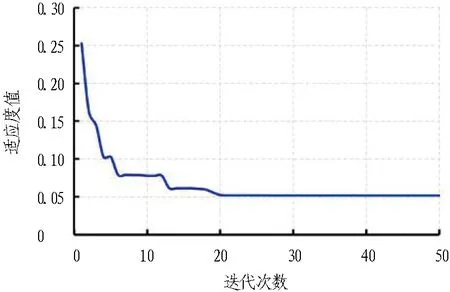
(a) 地铁车站拟合迭代误差图

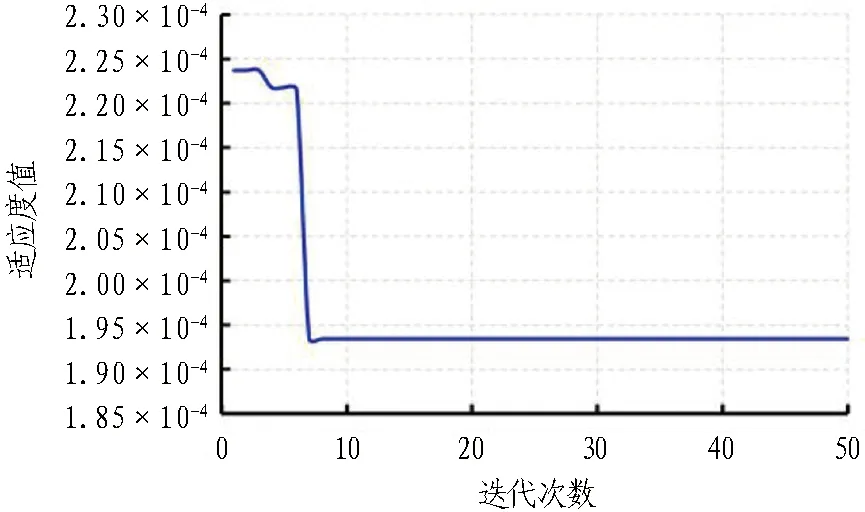
(b) 地铁盾构区间拟合迭代误差图图15 WOA-DELM拟合迭代误差图Fig. 15 Fitting iterative error diagram of WOA-DELM

由于地铁车站修建影响因素较多，且不同车站差异较大，而研究案例中地铁盾构区间断面为确定值，影响盾构区间碳排放的较大因素可考虑为盾构区间长度，导致最终预测结果盾构区间优于地铁车站，这从图13、图14和图15中的决定系数、评价函数和迭代速度可以看出。

3.3 碳排放输入指标敏感性分析

3.3.1 预测模型单因素敏感性分析

根据选择的WOA-DELM模型，对地铁碳排放主要输入指标进行敏感性分析，同时选取与该模型性能指标接近的ABC-DELM模型作为对比。分析过程中将各主要输入指标(地铁车站长度、车站宽度、车站高度、轨面埋深、楼层数、岛式站台宽度以及总建筑面积)按照表5单因素变化范围进行单因素敏感性分析。

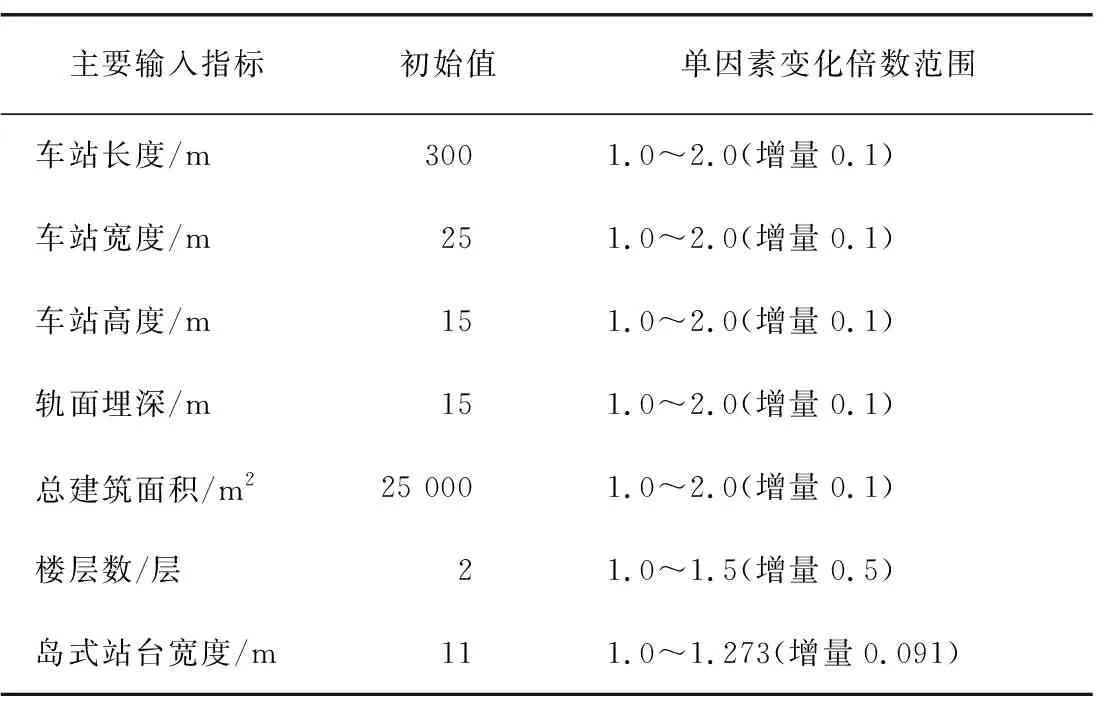
表5 地铁车站输入指标单因素变化范围Table 5 Variation range of metro station input index

地铁车站碳排放预测模型输入指标敏感性分析结果如图16所示。

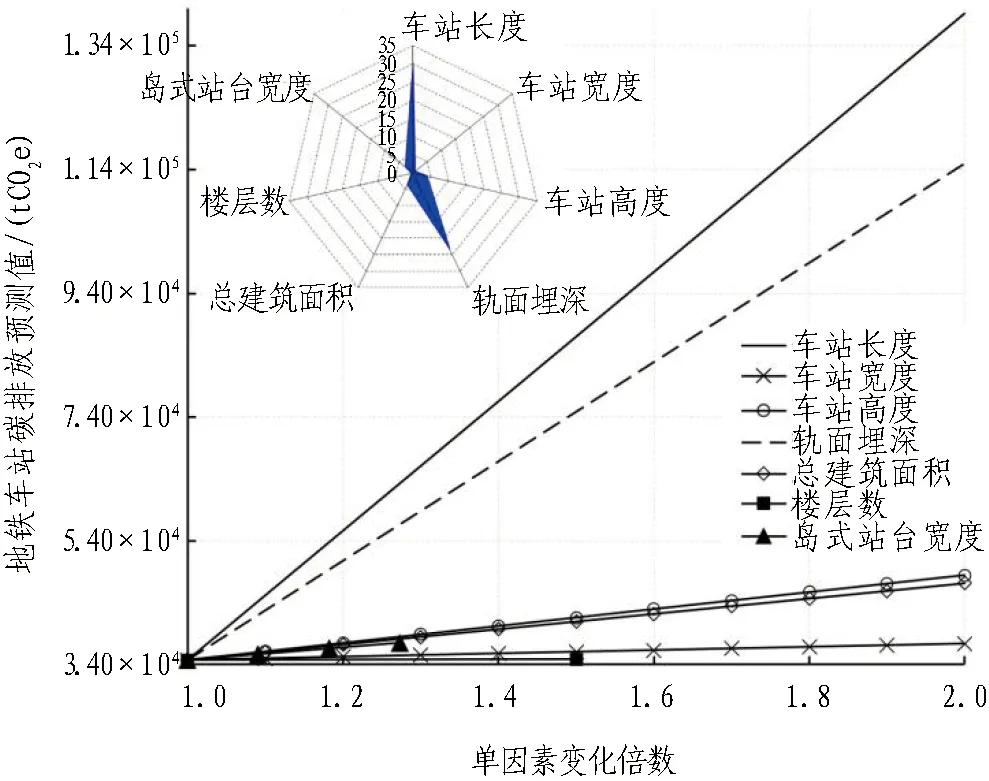
(a) WOA-DELM

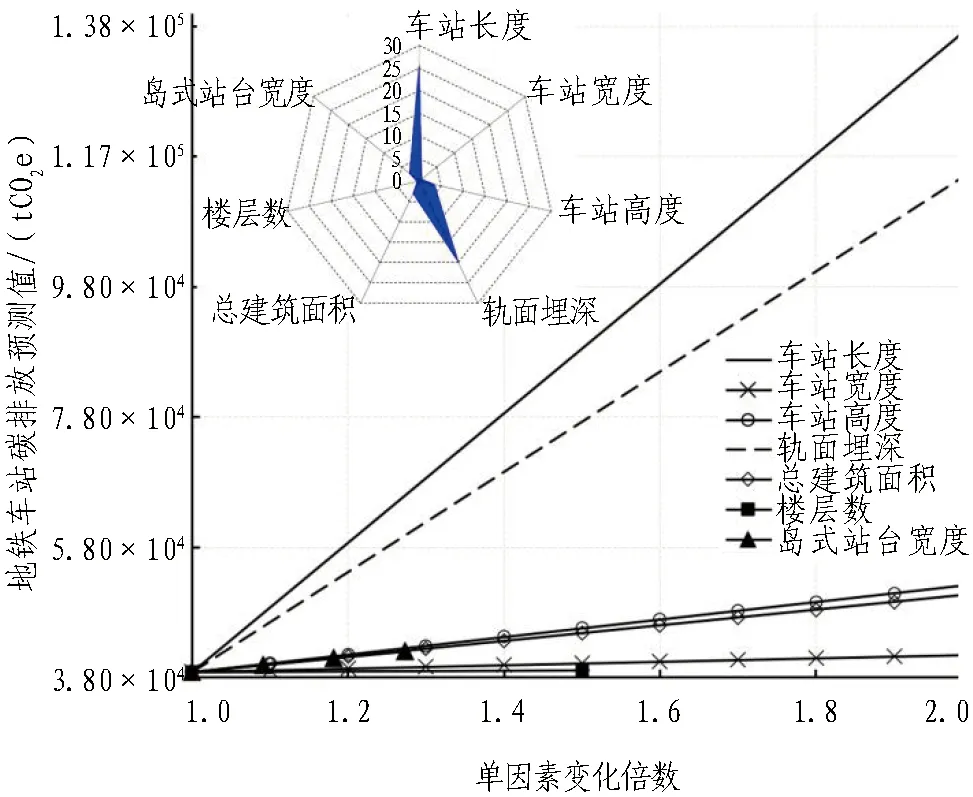
(b) ABC-DELM图16 地铁车站碳排放预测模型输入指标敏感性分析结果Fig. 16 Sensitivity analysis of carbon emission prediction model for metro station

从图16(a)中可以看出： WOA-DELM模型地铁车站碳排放量随着各输入指标的增大而增大。其中，碳排放量变化最大的输入指标为车站长度，车站长度每增加1 m地铁车站碳排放增加348.21 tCO2e，相对变化率为30.1%；其次为轨面埋深，相对变化率为23.1%，轨面埋深每增加1 m单位长度车站碳排放增加17.823 tCO2e；其余输入指标相对变化率按大小排序依次为地铁车站高度、总建筑面积、岛式站台宽度、地铁车站宽度和楼层数，相对变化率分别为3.9%、3.6%、2.7%、0.8%和0.4%。

从图16 (b)中可以看出： ABC-DELM模型各地铁车站碳排放量随输入指标的变化情况与WOA-DELM模型地铁车站碳排放量随输入指标的变化情况相同，最大相对变化率均小于WOA-DELM模型。其中，碳排放量变化最大的输入指标为车站长度，相对变化率为25.6%； 其次为轨面埋深，相对变化率为19.8%。由于案例中地铁车站的长度是地铁车站宽度的13～25倍，是地铁埋深的12～37倍，且总建筑面积为每层地铁车站长度与车站宽度乘积的总和，而选用的楼层数和岛式站台宽度变化较小，进而地铁车站长度在地铁车站碳排放中敏感性较高。

地铁盾构区间输入指标变化量仅为盾构区间长度和轨面平均埋深，敏感性分析结果为地铁盾构区间碳排放量随区间长度的相对变化率是随轨面平均埋深相对变化率的28倍。

3.3.2 地铁碳排放预测公式拟合

根据WOA-DELM预测模型输入指标敏感性分析结果，选用单位长度地铁车站碳排放量和轨面埋深作为地铁车站碳排放粗略预测的因变量和自变量，选用盾构区间碳排放量和盾构区间长度作为盾构区间碳排放粗略预测的因变量和自变量。地铁车站和盾构区间碳排放粗略预测拟合曲线分别如图17和图18所示。相应的碳排放预测公式见式(50)和式(51)。

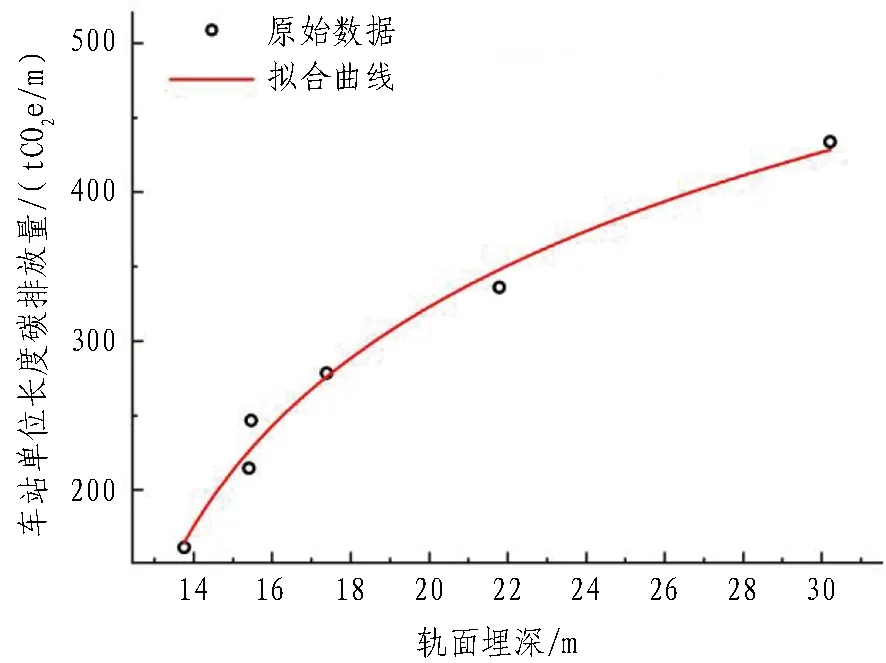
图17 地铁车站碳排放粗略预测拟合曲线Fig. 17 Carbon emission fitting curve of metro station

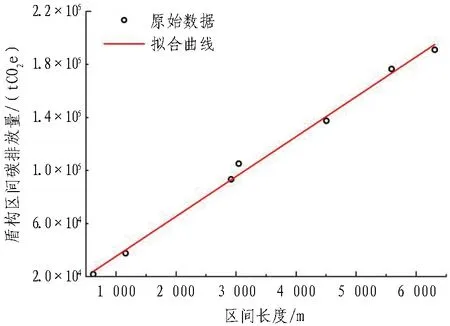
图18 地铁盾构区间碳排放粗略预测拟合曲线Fig. 18 Carbon emission fitting curve of metro shield section

y1=10.548+141.709×ln (x1-10.729)，

(50)

(51)

式(50)—(51)中：y1为地铁车站单位长度碳排放量，tCO2e/m；x1为地铁车站轨面埋深，m；y2为地铁盾构区间碳排放量，tCO2e；x2为地铁盾构区间长度，m；R1、R2分别为地铁车站和盾构区间碳排放拟合公式的相关系数。

为对比本文模型与其他模型的差异性，选取文献[14]中北京地铁地下双层双柱三跨岛式车站进行预测结果比较。根据文献[14]中地铁车站尺寸，采用本文WOA-DELM预测模型计算得到北京地铁车站碳排放量为40 592.491 tCO2e，按照本文式(46)计算得到北京地铁车站碳排放为75 645.573 tCO2e，与文献[14]计算得到的54 612.312 tCO2e分别相差25.6%和38.5%。在地铁碳排放影响因素中，本文研究结果与文献[14]研究得到的结论基本一致，即地铁车站碳排放随埋深增加而线性增加，随地铁车站宽度变化不明显，但采用本文模型计算得到的地铁车站碳排放随埋深的变化率为5 348.998 tCO2e/m，是文献[14]中计算得到的743.05 tCO2e/m的7倍多。文献[14]中计量的温室气体包含了CO，碳排放计算过程采用了分部分项计算，且建筑材料主要碳排放因子与本文不同，本文模型在计算地铁车站碳排放时结果与文献[14]存在较大差异。由于模型在预测过程中未考虑埋深变化引起的土方、围护结构和主体结构各分项工程的具体碳排放，从而在埋深单因素变化预测中与文献[14]相差较大； 同时，由于基于生命周期评价的碳排放计算具有较强的地域性，且WOA-DELM算法预测效果的优劣与测试数据相关联，导致结果存在较大差异。

4 结论与讨论

本文依托成都地铁18号线，对6车站7区间地铁建设阶段碳排放进行计算，采用WOA-DELM算法对地铁车站和盾构区间碳排放进行预测，并与其他智能优化的深度极限学习机预测结果进行对比，得到如下结论：

1)通过对地铁建设阶段的碳排放进行计算，筛选出不同建设阶段对地铁碳排放影响较大的材料。建筑材料生产阶段的碳排放量最大，其次是现场施工能源消耗所产生的碳排放。盾构区间在施工阶段产生的碳排放是地铁车站在施工阶段产生的碳排放的2倍。

2)建立了地铁碳排放WOA-DELM预测模型，通过和其他预测模型对比，验证了该模型在本案例研究中的有效性。通过该模型对地铁车站输入指标进行敏感性分析，得到了地铁车站碳排放的关键影响因素为地铁车站长度和轨面埋深。

3)选用地铁车站长度和轨面埋深拟合得到地铁车站建设阶段碳排放粗略预测公式，选用地铁盾构区间长度拟合得到盾构区间碳排放粗略预测公式，该预测公式可为地铁绿色设计减碳计算提供参考。

本文在研究对象、研究范围、模型的构建和选取以及结论适用范围方面均存在局限性，同时数据清单中未列举出碳排放较少的材料，存在的局限性具体如下：

1)本文研究的地铁车站碳排放针对的是成都市采用明挖法开挖的地铁车站土建工程碳排放，地铁盾构区间碳排放针对的是成都盾构面积为54.106 m2(盾构直径8.5 m)、管片厚度为0.4 m的地铁盾构区间土建工程碳排放。本文碳排放研究系统中时间边界为全生命周期中的建设阶段，包括建设阶段建筑材料生产、建筑材料运输和施工机械能耗；空间边界为构成地铁车站和盾构区间的土建实体、土石方工程运输机械能耗、模板和脚手架钢材消耗，其中不计量的内容包括人工消耗的碳排放、水资源碳排放、周转摊销碳排放以及其他碳排放较少的材料。

2)在地铁线路规划阶段，采用碳排放预测模型可以在地铁建设之前估算出碳排放量，为地铁选线设计提供参考。本文采用预测模型对地铁碳排放进行回归预测，且为寻求最优的碳排放预测模型，对比了DELM、KELM、BP、支持向量机和ELM算法。由于支持向量机和ELM预测误差较大，未在文中列出，而DELM预测效果较好，从而对DELM进行了优化，以获取更优的预测模型。虽然文中选用样本较少，但神经网络预测和普通回归预测原理大致相同，最终拟合获得的相关变量的相关系数，能从一定程度上反映各机器算法的优劣及本文研究对象和研究范围下地铁碳排放的预估值，后期将搜集更多地铁相关数据对该模型进行验证和拓展。

3)由于研究范围的局限性，本文得到的预测模型及相关结论仅局限于本文研究范围下的成都地铁车站及盾构区间碳排放的评价和预测。