基于岩屑分形维数的岩石脆性评价方法

常小龙 曹 旭 刘 锐 方少伯 孙志高 田泽华

（中国石油西部钻探工程有限公司录井工程分公司）

0 引言

岩石脆性指数是水平井压裂施工设计的关键参数之一[1-2]。现有脆性评价指标近20 种，包括基于强度、全过程应力-应变曲线、加卸载实验、硬度测试、成分分析等评价指标[3]。目前常用弹性参数法和矿物组分法评价岩石脆性[4]。其中，弹性参数法是通过归一化的杨氏模量和泊松比来评价岩石脆性[5]，但因杨氏模量最大值和最小值确定方法不统一，不同区域岩石脆性无法对比，且杨氏模量和泊松比在脆性评价中的权重不确定，岩石脆性评价存在不确定性。矿物组分法是通过分析石英、方解石和黏土等矿物含量来评价脆性[6-10]，该方法操作简单，但受限于实验选样、制样等因素影响，时效性差，单样成本较高。此外，还有利用声波、元素等测井资料评价岩石脆性[5]，这两种方法虽经济方便，但仍难以满足水平井对脆性指数的实时且精细评价需求。

近年来，国内外学者引入分形概念[11-16]，认为岩屑颗粒分布函数可用Rosin-Rammler 和Gaudin-Schuhmann（G-S）分布函数表征[12]，前者分布函数趋向粗粒端，后者趋向细粒端，即G-S 函数更符合岩屑分布规律[15]，但基于岩屑分形维数计算岩石脆性指数鲜有研究。为此，笔者提出一种以岩屑分形维数快速获取岩石脆性指数的方法，即通过研究岩屑分布规律并计算其分形维数，建立其与岩石脆性指数相关性模型，实现无需矿物组分或力学实验测试，仅以岩屑分形维数计算岩石脆性指数。

1 岩屑分形规律及分形维数计算

1.1 岩屑分布规律

分形理论是对自然界极复杂且不规则的结构、现象进行定量描述的方法，岩石经钻头破坏后虽然形成形态各异的岩屑颗粒，但从统计中仍满足自相似规律，现常用公式（1）Rosin-Rammler 函数和公式（2）Gaudin-Schuhmann函数描述岩屑颗粒分布规律[12]。

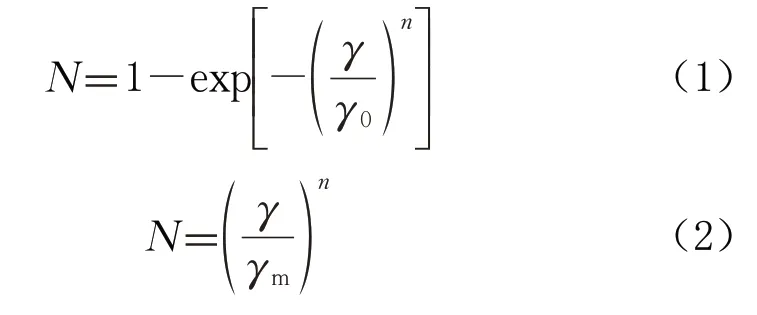
上式中：N为岩屑粒度小于γ的相对累积量，%；γ为岩屑颗粒尺寸，mm；γ0为粒度特性系数；n为均匀性系数；γm为岩屑粒度分布直线与N＝1直线交点的γ值。

将公式（1）按级数展开后，舍去第二项及后面多项，即可得到公式（2），表明当岩屑粒度较小时，两个分布函数均可用于描述岩屑颗粒分布规律。研究认为，公式（1）适用于颗粒分布趋于粗粒端，公式（2）适用于颗粒分布趋于细粒端[15]。

1.2 岩屑样品选取及标准化处理

在某研究区域选取5～8口井岩屑样品，样品经清洗烘干后质量为150～200 g 为宜。直井段取样选取一定深度范围，该范围岩性应包括泥岩、砂岩以及地层其他岩性，保证岩性多样性；水平段样品为全水平段范围内取得，取样间隔50～100 m，以保证样品既能反映水平段不同位置岩性的非均质性，也尽可能降低后续分析工作量。

岩屑样品是从井底破碎后通过钻井液携带至地面的，在井筒中经长时间浸泡、冲刷，使得部分泥岩软化分散，此外还有诸多工程因素影响岩屑颗粒的分布规律，因此需对其进行标准化处理[17]。处理方法为：将岩屑样品放入颚式破碎仪二次破碎处理，设备转子转速为100～1000 r/min，进、出料粒度分别为≤45 mm 和≤0.5 mm，然后再进行岩屑粒度分布分析和分形维数计算。

1.3 岩屑分形维数计算

将标准化处理后的岩屑通过不同方形孔筛网筛选，孔径记为γ（ii为不同孔径），筛子孔径选取至少5种以上，以获得足够的数据量用于回归分析。以筛选粒径小于γi的岩屑样品被筛选漏下去的颗粒质量记为M下（γi），对应的留在筛网上的记为M（γi），颗粒总数记为N（γi）。称重天平量程为0～250 g，精度为0.001 g。

岩屑样品二次破碎后粒度分布遵循质量与频率分布关系：

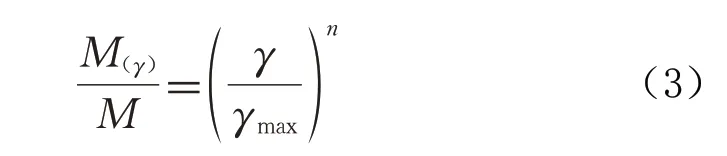
对公式（3）两边求导有：

将岩屑破碎后定义为一种破碎体分形：

考虑破碎体质量、尺寸、数量间关系[18]：

由公式（5）和公式（6）可知岩屑质量和颗粒粒径关系为：

由公式（4）和公式（7）可知：

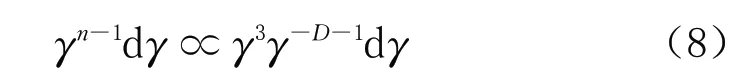
因此，由公式（8）可得到分形维数D的表达式为：

上式中：γmax为岩屑最大粒径，mm；M为岩屑样品总质量，g；C为常数；D为分形维数，无量纲；V为岩屑颗粒体积，mm3。

在直角坐标系上绘制散点图，散点横坐标X值为lnγi，纵坐标Y值为ln（100M（γi）/M），并进行直线回归，测定回归直线斜率即为均匀性系数n，可计算得到岩屑分形维数D。

取研究区X 井区5 口水平井：J 1 井井深2820、2 870 m，J 2井井深3100、3200、3300 m，J 3井井深1680、1730 m，J4 井井深2960、3060 m 及J 5井井深2110、2 210、2310 m处共取得12组岩屑样品，每组样品清洗烘干后质量为150 g左右，再对每组样品用2至80目筛网筛选，获得不同粒径的岩屑质量，结果见表1。

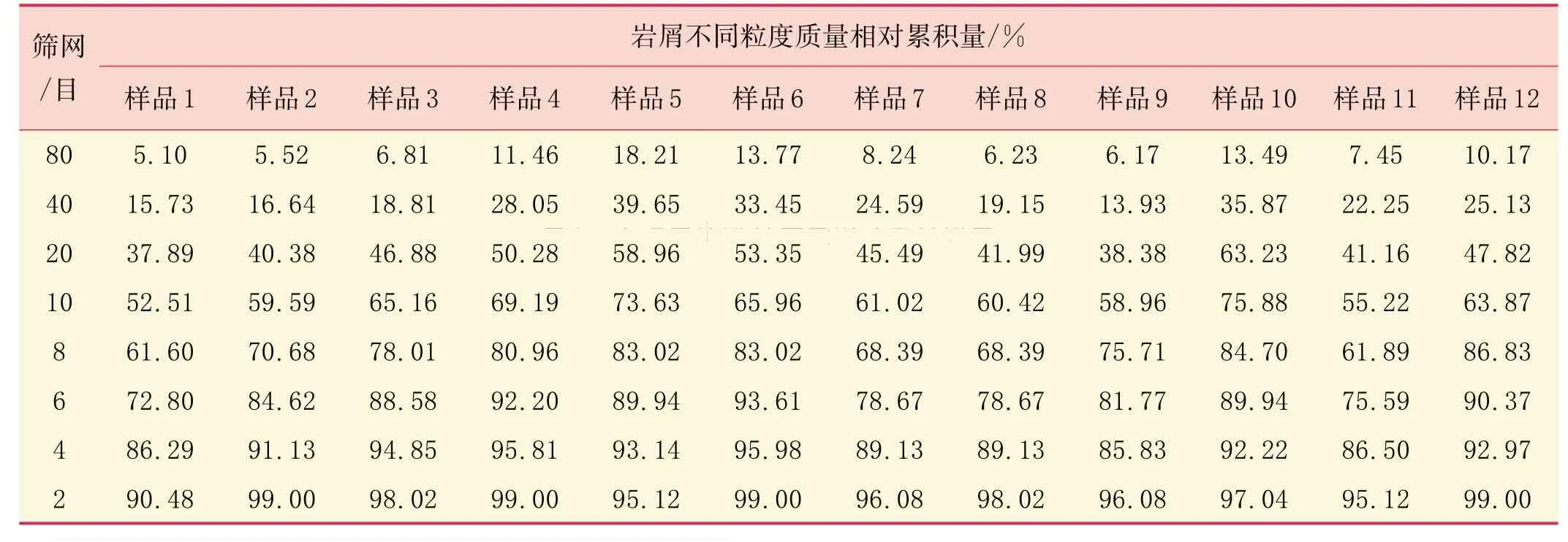
表1 上返岩屑筛分质量累计百分比

利用岩屑样品的粒度分布关系绘制相应的分形曲线（图1），通过线性回归分析计算得到分形维数D，结果见表2，相关性系数r2平均大于0.89，证明岩屑具有很好的分形特征。

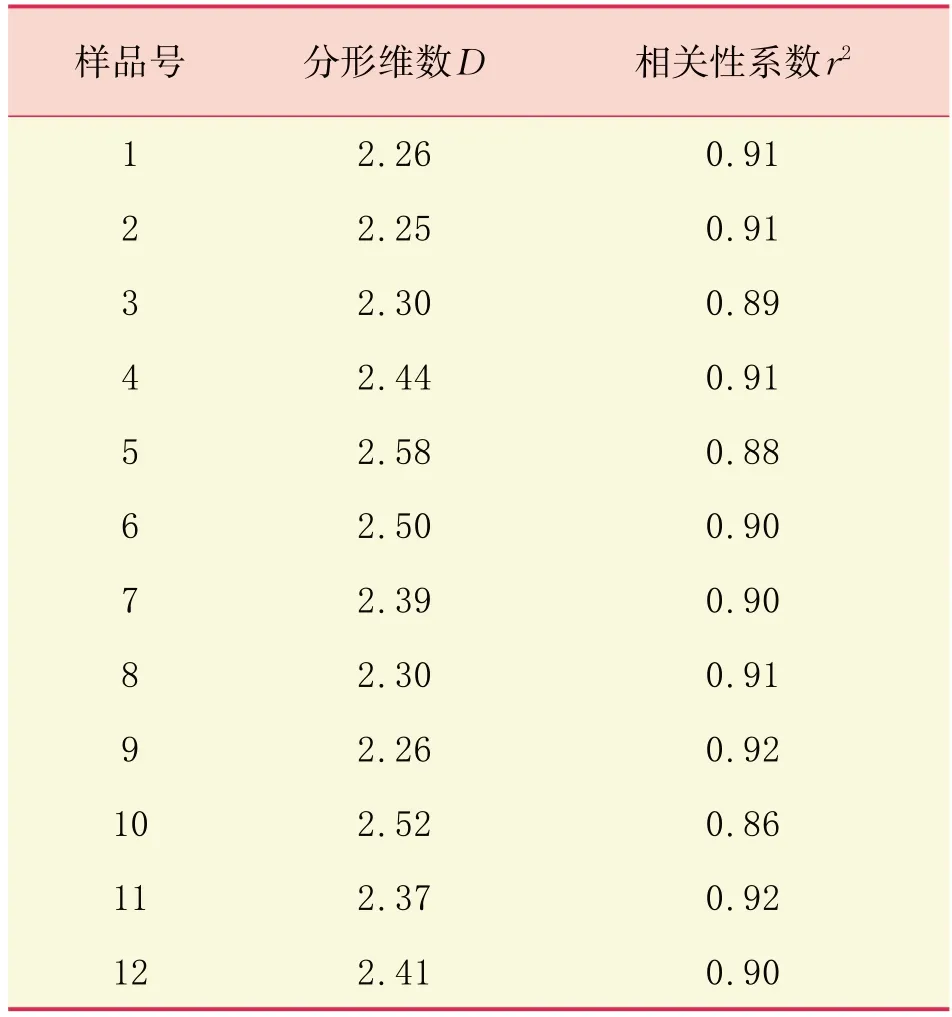
表2 12组岩屑样品分形维数计算结果

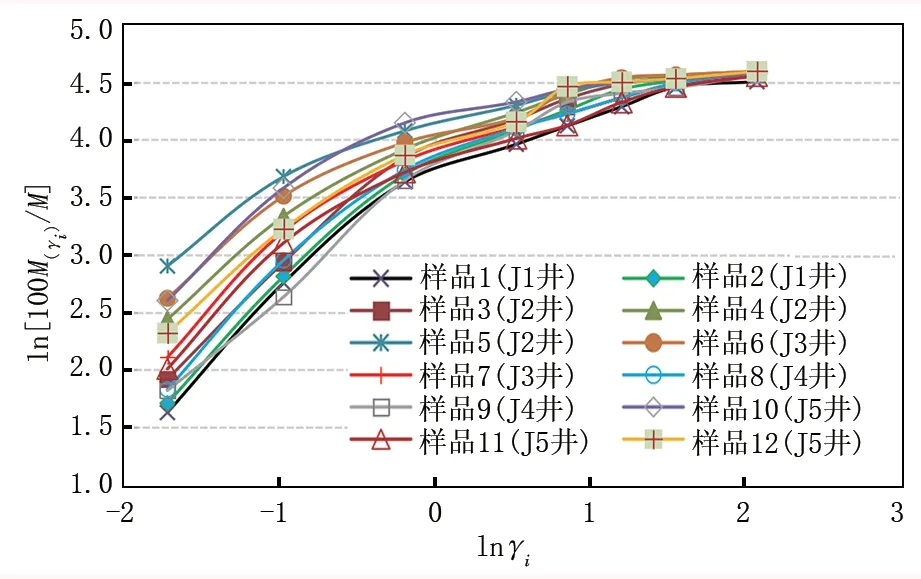
图1 12组岩屑样品分形曲线

2 基于矿物组分法的岩石脆性指数计算

基于矿物组分计算岩石脆性方法较多，多以脆性矿物与总矿物含量之比作为脆性指数，见公式（10）。各计算公式仅在脆性矿物种类选取方面存在差别，这种脆性矿物计算思路虽被行业普遍接受，但均未考虑岩石自身物理性状，且近似认为每种矿物对岩石脆性贡献权重相同，这显然不符合实际情况。

岩石脆性反映岩石综合的力学特性，应既考虑岩石矿物组成，也不可忽略岩石物理属性，因此以矿物力学参数修正，见公式（11），即：

因杨氏模量表征岩石的抗压物理属性，杨氏模量越大，越难发生形变，其反映岩石受破坏后裂缝张开的能力。泊松比是岩石受力横向变形能力，因此可用杨氏模量和泊松比作为岩石脆性修正系数，即：

水平井储层的常见矿物中石英和黄铁矿脆性最强，方解石次之，但其含量偏低，而长石和黏土最差，因此岩屑脆性指数可表示为：

上式中：BI为脆性指数，无量纲；Wbrit为脆性矿物含量，%；Wtotal为总矿物含量，%；αj为脆性指数修正系数（分别为石英、长石、黄铁矿、黏土等矿物对应的脆性指数修正系数），无量纲；Yj为第j种矿物杨氏模量，GPa；Pj为第j种矿物泊松比，无量纲；W石英为石英矿物含量，%；W黄铁矿为黄铁矿矿物含量，%；W长石为长石（碳酸岩）矿物含量，%；W黏土为黏土矿物含量，%。

对研究区X井区5口井12组岩屑样品的矿物含量分析统计可知（表3），岩屑成分以石英为主，占40.3%～47.9%，平均值为45.2%，长石和黏土矿物次之，分别为27.5%～36.3% 和16.1%～31.6%，平均值分别为32.6%和21.8%，黄铁矿含量最少，仅为0～0.7%。

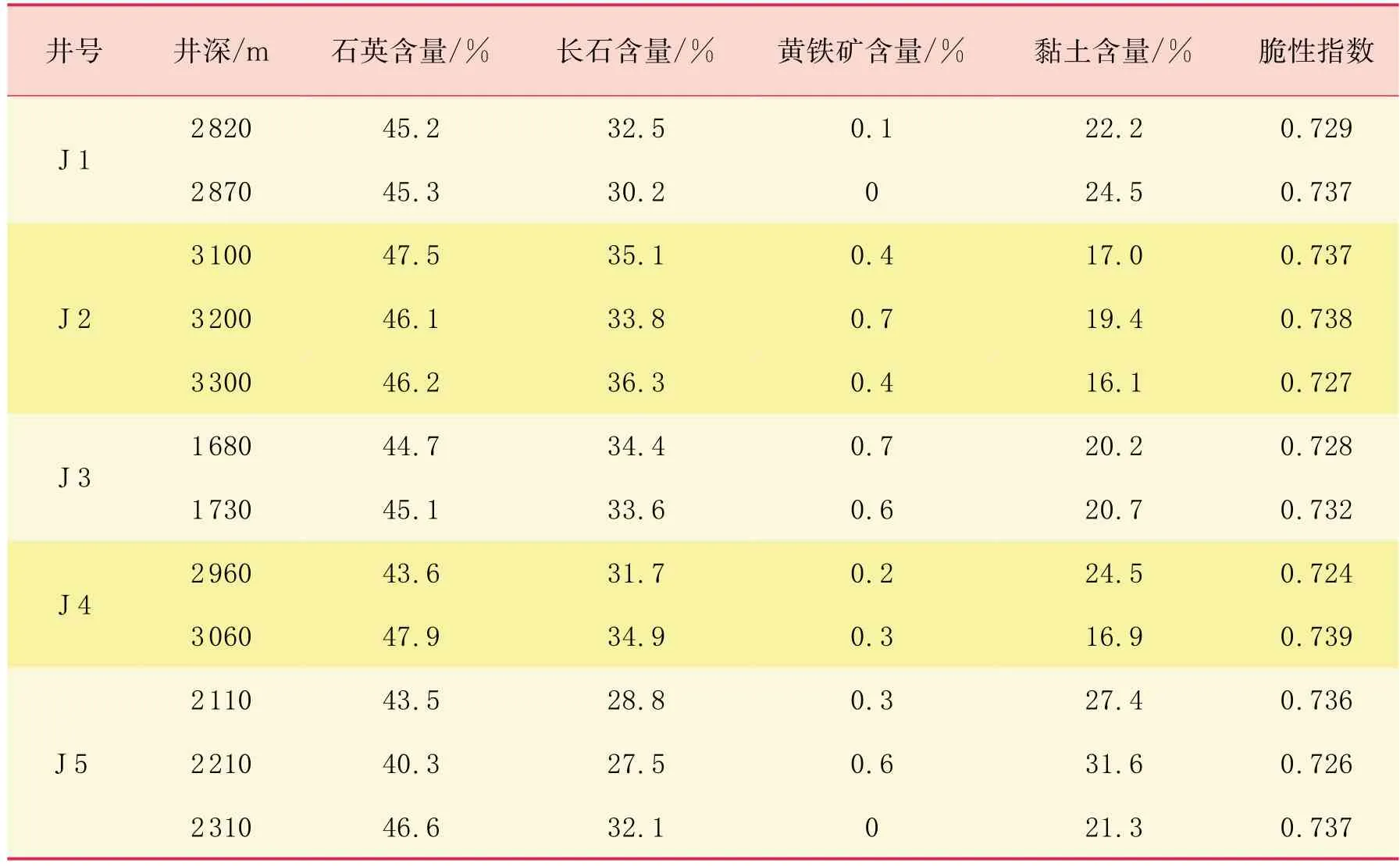
表3 5口井12组岩屑样品矿物含量统计

3 岩屑分形维数与脆性指数相关性建模

在研究区5 口井12 组岩屑样品中，取样品2、样品5、样品6、样品8、样品9、样品10 和样品11 的岩屑矿物计算岩石脆性指数与岩屑分形维数做相关性分析（图2），相关性模型为：

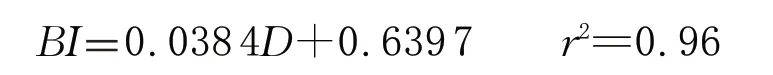
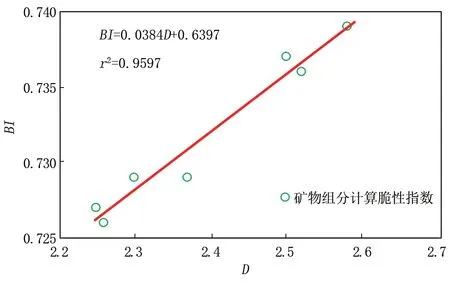
图2 岩屑分形维数与脆性指数相关性分析

取样品1、样品3、样品4、样品7 和样品12 进行误差分析（图3）。

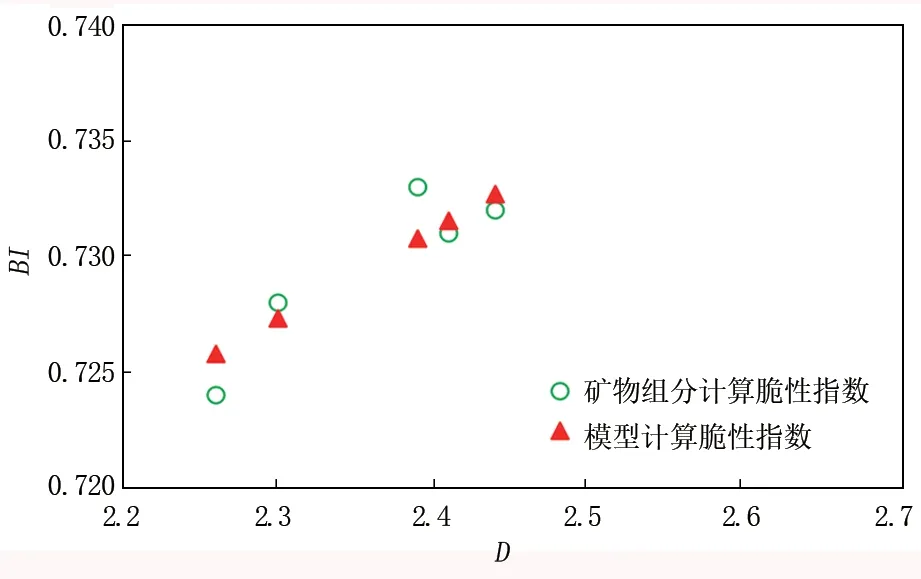
图3 岩屑分形维数与脆性指数相关性模型验证

通过模型计算得到样品1、样品3、样品4、样品7和样品12的脆性指数BI分别为0.726、0.728、0.733、0.731 和0.732，对照矿物组分计算结果误差分别为0.25%、0.09%、0.01%、0.30%和0.07%，表明误差较低，可以满足现场分析需求。

4 实例分析

取研究区X井区的正钻井J 8井井深2220、2270、2320、2370 m 处和正钻井J 10 井井深3060、3160、3260 m 处共7组岩屑样品，清洗烘干再经二次破碎后每组样品质量为150 g 左右，再用2 至80 目筛网筛选，获得不同粒径的岩屑质量，利用岩屑样品的粒度分布关系，线性回归分析计算得到分形维数D（表4）。

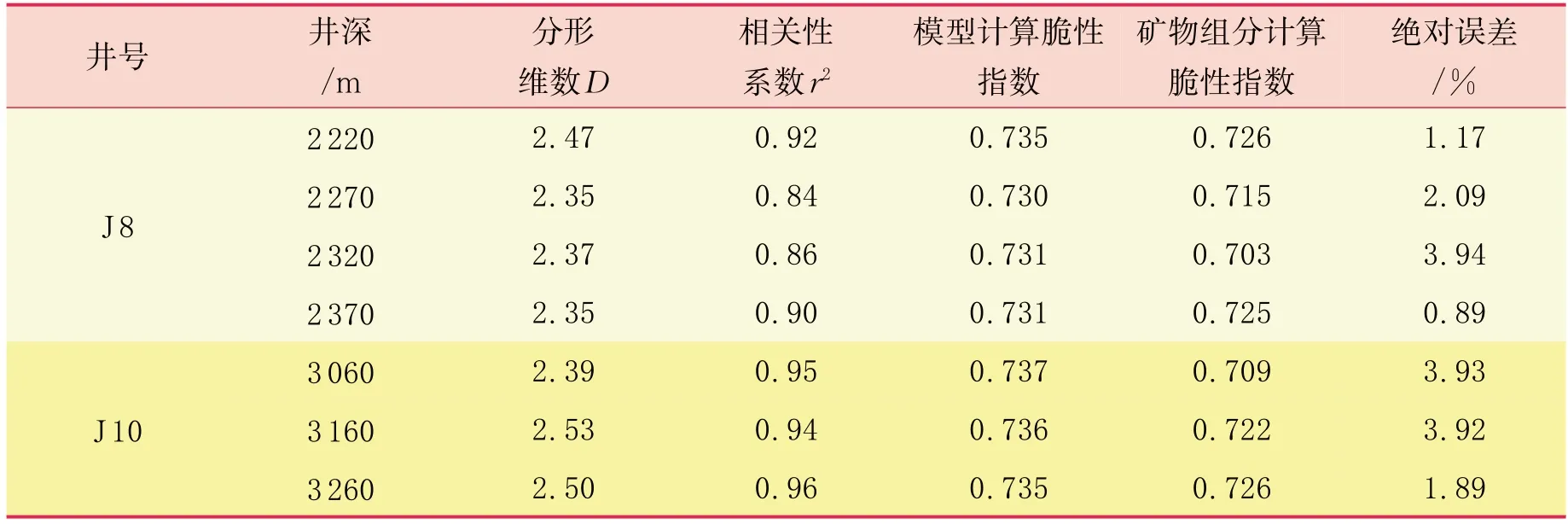
表4 J 8和J 10井水平段不同井深的脆性指数计算结果

对研究区X 井区J 8 井、J 10 井的7 组岩屑样品矿物组分进行分析，并计算出脆性指数，再以研究区已建立的岩屑分形维数与脆性指数相关性模型（BI＝0.0384D+0.6397）计算脆性指数对比，结果显示两者绝对误差小于4%，即该模型可以用于该区块水平段岩石脆性指数的计算。

5 结论

（1）水平段岩屑分形规律符合G-S 分布函数，分形维数相关性系数r2平均大于0.89，具有明显的分形特征，岩屑分形维数与矿物组分法计算的岩石脆性指数相关性系数r2为0.95，即可用岩屑分形维数计算岩石脆性指数。

（2）邻井应用岩屑分形维数与脆性指数相关性模型计算结果显示，该方法与矿物组分法计算结果的绝对误差小于4%，可以为水平段压裂施工参数优化提供一定指导。但其他如岩屑分形维数与储层可压性以及裂缝扩展情况等有待进一步研究。

（3）基于岩屑分形维数计算岩石脆性指数是一种低成本和高时效性的现场应用方法，为录井行业深度挖掘岩屑信息并指导钻井工程施工提供了一种新的思路。