基于二次逆可靠度分析方法的边坡稳定性研究
高乐星 梁 斌 吴 政 贺 敏
(湖南工业大学土木工程学院,湖南 株洲 412007)
在进行边坡稳定性分析和评估时,岩土体的基本参数、边坡的破坏模式和外荷载等因素以及它们的变异性,都是我们需要进行考量的。此等情况下,运用边坡稳定性分析方法中的确定性分析方法显然不合适,不确定性分析方法中的可靠度方法[1-2]是基于概率统计,充分考虑存在的不确定性因素,最终以可靠度指标β或失效概率Pf来衡量边坡的稳定性的一种方法。但是单纯依靠β或Pf评价边坡的稳定程度在实际工程中应用起来并不方便,传统确定性方法又过于单调。因此,为打破传统安全系数法和可靠度方法的单一性限制,寻求更加灵活的稳定性求解方法,将可靠度方法与传统的安全系数法结合起来,本研究提出一种可靠度指标加稳定性系数的二元综合评价体系[3],形成逆可靠度分析方法。
以可靠度理论为基础,逆可靠度分析法[4]为给定结构可靠度指标β(失效风险)的前提下,逆向求解结构的安全系数,继而进行调整以保证结构的安全性。至今,已有诸多学者对此进行了研究与探索。Winterstein S R 等[5]运用一次逆可靠度方法成功估算了海边建筑结构的设计荷载,奠定了其在逆可靠度方法中的核心地位。程进等[6]将一次逆可靠度法应用至求大跨悬索桥主缆稳定性系数并给出了迭代方法。Chen Jin 等[7]把一次逆可靠度和人工神经网络相融合,进而分析结构隐式功能函数问题。李隐[8]则在边坡工程中采用一次逆可靠度方法,反向推演边坡的黏聚力、内摩擦角和坡角。罗正东等[9]针对边坡的稳定性问题使用一次逆可靠度方法并对边坡的影响因素进行了敏感性分析。一次逆可靠度方法已发展得相对成熟,应用广泛。
在此背景下,针对逆可靠度分析方法的研究一直停留在一次逆可靠度法研究领域内的现状,为了丰富逆可靠度分析方法,加速逆可靠度分析方法的发展进程,以及扩展边坡稳定性分析方法,本研究提出二次逆可靠度方法。该方法将可靠度指标加稳定性系数作为综合评价指标,对边坡进行稳定性分析,能很好地适应工程目标可靠度指标的变化,同时,把二次二阶矩法融入至逆可靠度思想中,在一次逆可靠度方法的基础上进一步提升精度,达到主动控险和降低工程造价的目的,对于安全缩减现今边坡设置保守的安全储备、节约工程成本具有十分重要的实际工程意义。
1 二次逆可靠度法基本原理
与一次逆可靠度分析方法类似,二次逆可靠度是对于既定的目标可靠度指标βt,在一定的约束条件下根据结构的极限状态方程确定设计参数。以上可归结[10]为:给定目标可靠度指标βt和约束条件的前提下求设计参数θ,约束条件表达为

式中,Q(u)为极限状态方程;x、θ为基本随机变量,变换至标准正态空间为u=(ux,uθ),ux=(ux1,ux2,…,uxn),θ为待求设计参数。

x和θ则通过式(2)和式(3)求累计分布函数Fxi(·)和Fθ(·)的反函数获得;φ(·)为标准正态分布函数。
二次逆可靠度方法其实是对一次逆可靠度方法的一种修正,除了利用极限状态方程的梯度外,还将其二阶导数纳入考虑范围,更加全面地考虑了极限状态曲面在验算点附近的非线性比如曲率、凹向等性质。其原理是采用正可靠度方法中的二次二阶矩法对结构的极限状态方程Q进行反复迭代,直到找到一个θ值以满足目标可靠度指标βt为止。
根据验算点法可知标准正态变量u和目标可靠度指标βt在验算点处满足:

式中,∇uQ表示极限状态方程Q在u处的梯度向量。
联立式(4)和式(5),得:
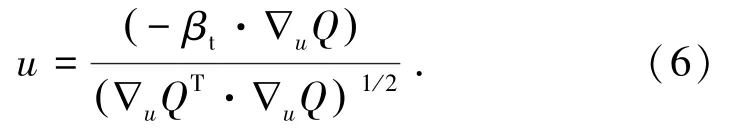
这样,约束条件Q(u)=q(x,θ)和式(5)就共同构成了求解二次逆可靠度问题的要素。
将极限状态函数Q在假设的待求参数初值θ0处,应用Taylor 级数展开并截取至2 次项:

根据设定的初始值u0和θ0计算得到∇u0Q及∂Q(u)/∂θ0,然后通过式(6)和式(7)计算得到新的随机变量u1和新的设计参数θ1,再视u1和θ1为新的初始值,进行反复迭代计算,直到满足收敛条件式(8)时止。

式中,um和θm分别为第m次迭代计算得到的随机变量值与设计参数值;收敛精度ε1、ε2的取值范围一般为10-4~10-3。
2 边坡稳定二次逆可靠度求解方法
2.1 极限平衡理论中的简化Bishop 法
作为边坡可靠稳定性分析中最经典的算法,极限平衡法因简便适用、逻辑严谨、精度较高一直沿用至今,期间以此为基础形成了多种不同的分析方法,包括Bishop 法、简布法、摩根斯坦—普瑞斯法、萨尔玛法等[11]。
本研究采用的简化Bishop 法是由瑞典圆弧法优化而来[12]。与传统的瑞典圆弧法相比,简化Bishop法计算安全系数时忽略了条间剪力,并假定土条之间的力是水平的,土条底面上的法向力由在竖直方向上的静力平衡条件求出,根据边坡整体力矩平衡来确定边坡的安全系数FS。其表达式[13]为
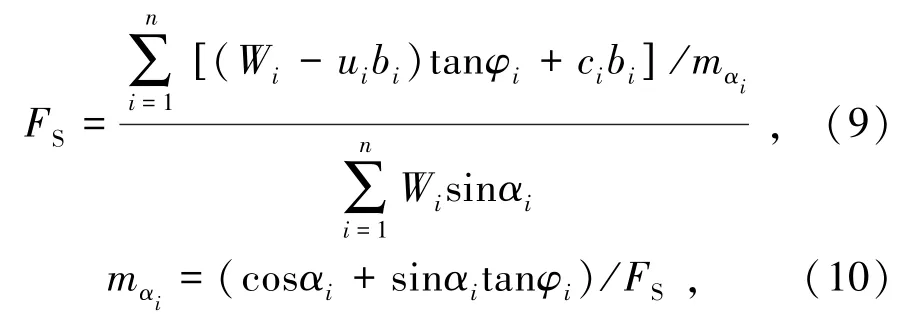
式中,FS为安全系数;ci为黏聚力;φi为滑面内摩擦角;Wi、bi、αi分别为第i个条块重力、宽度、网弧底面倾角;ui为第i个条块孔隙水压力。其中,Wi、bi、αi、ui的取值与滑面半径R有关。
2.2 基于二次逆可靠度方法反推安全系数
在运用二次逆可靠度方法对边坡进行稳定性分析时,任何力学参数或稳定性系数都可作为待求系数θ。本研究主要针对边坡的安全系数FS进行逆向分析。一般考虑土体的黏聚力c,内摩擦角φ和重度γ这3 个重要参数,将它们视为3 个相互独立的基本随机变量且服从正态分布,即ux= (γ,c,φ),设μγ、μc、μφ和σγ、σc、σφ,分别为γ、c、φ的均值和标准差,则ux=(μγ±λσγ,μc±λσc,μφ±λσφ),根据文献[14]中的3 倍均方差原则取λ=3。结合简化Bishop 模式下的极限状态方程式(9)和式(10)得二次逆可靠度下的边坡极限状态方程为

u0和θ0为u和θ的初始值,由式(11)和式(12)求得Q在u0和θ0处的梯度表达式:


u1通过式(15)求得,θ1则通过解式(16)获得。如此,再将u1、θ1作为下一轮的初始值进行反复迭代,直到满足所设的收敛精度ε1、ε2为止。最后求得的θ即为既定可靠度指标下的安全系数FS。
2.3 基于二次逆可靠度的边坡稳定具体分析步骤
综上,边坡稳定性二次逆可靠度分析方法具体流程可归纳如下。
(1)利用有限元软件搜索边坡的潜在破坏滑动面,确定其滑面半径并完成滑动体条块划分。
(2)建立简化Bishop 模式下的边坡功能函数,并选取基本随机变量且将其正态化,本身就是正态变量的无需进行这一步。

(4)将所求梯度代入式(6)、式(7),计算出u1、θ1后再将其作为新的初始值重新代入式(6)、式(7)中。反复迭代直至达到式(8)所设收敛精度。
(5)满足收敛精度的θm即为事先给定失效风险下的待求安全系数FS。
3 算例分析
以一均质边坡[15]为例,高20 m,坡比为1 ∶1。其土层参数信息:泊松比ν=0.3,弹性模量E=20 MPa,重度γ=20 kN/m3,黏聚力c=40 kPa,内摩擦角φ=20°。c、φ相互独立,均服从正态分布,变异系数都为0.1。
如图1所示,利用有限元软件确定出该边坡潜在滑动面半径为33 m,于是选取R=33 m 的滑动圆弧进行分析,图2为边坡滑动面的条块划分,计算中条块的宽度取b=3.3 m,设边坡的目标可靠度指标βt=3.0,对应失效概率Pf= 0.135%,u0=(μγ0,μc0,μφ0) =( 20,40,20),θ的初始值设为1.0,然后按照上述求解步骤进行求解。

图1 边坡潜在滑动面示意Fig.1 Schematic of potential sliding surface of slope

图2 边坡滑动面条块划分Fig.2 Slope sliding noodle block division
通过式(13)、式(14)求得初值点处的梯度为

将以上各值代入式(15)、式(16)进行计算得

再把u1和θ1的值赋给u0和θ0开始下一次迭代,经过8 次迭代后达到之前式(8)所设的收敛精度(设ε1,ε2都取10-3)。迭代过程见表1。
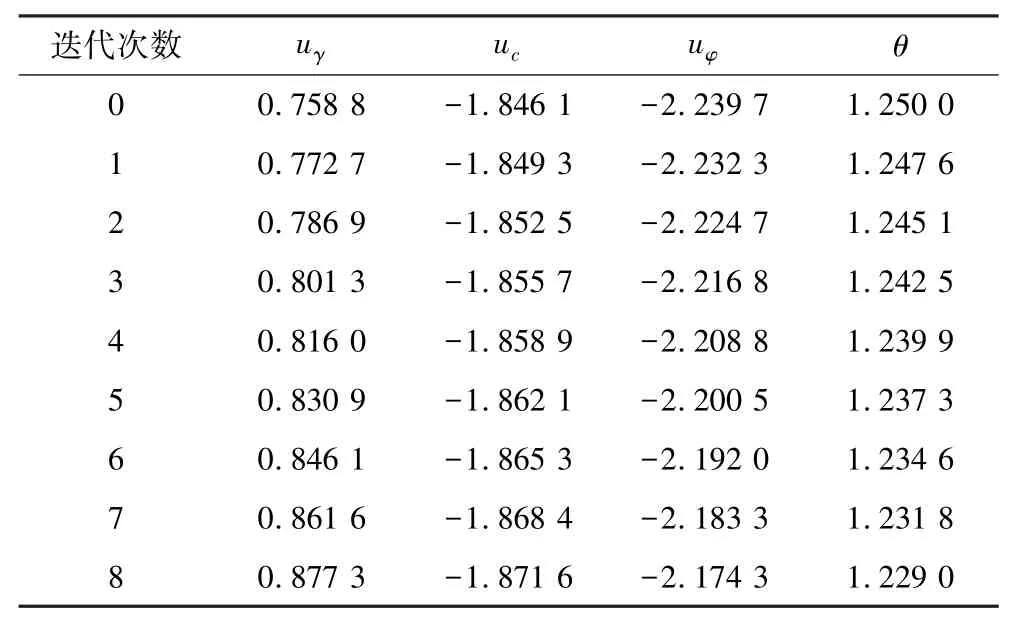
表1 二次逆可靠度迭代求解过程Table 1 Iterative solution process of quadratic inverse reliability
最后得u8=(0.877 3,-1.871 6,-2.174 3),θ8=1.229 0。即在失效风险概率Pf=0.135%,可靠度指标βt=3.0 的情况下,利用二次逆可靠度反向推演出边坡的安全系数Fβt=1.229 0。对于此边坡算例,利用一次逆可靠度以及简化Bishop 法求解安全系数,其结果对比见表2。

表2 3 种不同方法计算结果对比Table 2 Comparison of calculation results of three different methods
3 种方法求出的安全系数FS均大于1,证明该边坡满足稳定性要求,且一次逆可靠度方法和本文提出的二次逆可靠度方法所求FS均小于利用简化Bishop法求得的FS,是因为一次和二次逆可靠度方法在反演求边坡的FS时,不仅关注到了岩土体参数是时刻变化的,还将边坡目标可靠度和失效风险纳入了考虑当中。表中结果还显示二次逆可靠度方法的精度要明显高于一次逆可靠度方法,对于边坡失效风险的把控做到更加精准。
4 工程实例分析
4.1 工程概况与安全系数计算
某二级公路路基旁一均质粘性土坡,坡高H=10 m,坡角为45°,土体黏聚力c=24 kPa,内摩擦角φ=13.3°,c、φ均服从正态分布且相互独立,变异系数均为0.1,重度γ=18.6 kN/m3,泊松比ν=0.3,弹性模量E=10 MPa。
利用有限元软件FLAC3D进行数值模拟得到此边坡的安全系数FS=1.309,如图3所示。

图3 边坡计算安全系数Fig.3 Slope calculation safety factor
4.2 二次逆可靠度方法反推安全系数
首先确定边坡滑动面并划分条块,如图4所示。其滑动圆弧半径为17.5 m,条块宽度设为b=2 m。
图4 边坡滑动面条块划分Fig.4 Slope Sliding Noodle Block Division
然后设边坡的目标可靠度指标βt= 2.2,u0=(uγ0,uc0,uφ0) = (18.6,24,13.3),θ的初始值设为1.0,然后按2.3 节求解步骤进行迭代计算。最后得um= (1.787 3,-2.123 3,-1.138 9),θm= 1.151 9。即在可靠度指标βt=2.2 的情况下,利用二次逆可靠度反向推演出边坡的安全系数Fβt=1.151 9。与其他方法对比结果如表3所示。

表3 不同方法计算结果对比Table 3 Comparison of calculation results of different methods
根据表4,《JTG D30—2015 公路路基设计规范》中的路堑边坡稳定安全系数表知,正常工况下,二级及二级以下公路的边坡稳定系数的范围为1.15 ~1.25。本文方法所求安全系数 ,满足规范要求。

表4 路堑边坡稳定安全系数Table 4 Safety factor of cutting slope stability
表3中所有方法求出的安全系数FS均大于1,表明该边坡满足稳定性要求,有限元法求得的安全系数FS值最大,其安全储备也最大,简化Bishop 法次之,一次逆可靠度法在参数复杂性和失效风险双重控制下所求的FS值小于前2 种方法,而本文提出的二次逆可靠度方法在一次逆可靠度方法的基础上又提升了精度,不仅能更加精确地调控边坡的失效风险,同时在保证安全性的前提下也有效地节约了工程成本。
5 结 论
(1)由于安全系数法和可靠度方法的局限性,本文在一次逆可靠度方法的基础上将两者结合起来,针对边坡工程建立起了一种精度更高,具备可靠度指标和安全系数双重控制指标的稳定性综合评价体系。
(2)算例以及工程实例分析表明:本文提出的二次逆可靠度方法切实可行,精确度高,这对现今边坡的安全储备设置过大而造成的工程浪费现象具有很强的现实意义。
(3)本文仅对均质边坡的稳定性进行了二次逆可靠度评估,后续如何将其推广至非均质边坡,加强基于二次逆可靠度边坡稳定性分析方法的普适性,这是我们需要考虑的问题。

