含软弱夹层边坡地震动力响应及变形破坏机制研究
盛建龙 严寒冰 胡 斌 王庭元 钟卓希
(1.武汉科技大学资源与环境工程学院,湖北 武汉 430081;2.冶金矿产资源高效利用与造块湖北省重点实验室,湖北 武汉 430081)
地震是边坡发生失稳破坏的主要诱因之一,据中国地震台网数据统计,2021 年我国发生5 级以上地震37 次,对矿山边坡的安全产生了严重的威胁。研究地震作用下边坡的稳定性问题对于矿山开采和工程建设具有重要意义。
目前,国内外学者在此问题上做了大量的研究,取得了丰硕的成果。在极限平衡分析方面,罗红明等[1]基于刚体极限平衡法,提出了一种考虑地震力最危险方向的计算方法,并应用于实际滑坡稳定性评价。罗强等[2]运用强度折减法和极限分析上限定理,推导了边坡稳定性安全系数的计算公式。邓东平等[3]运用极限平衡的思想,在直线、圆弧和任意曲线3 种滑动方式下,推导了地震作用下边坡安全系数计算公式,并研究了坡体参数对边坡稳定性的影响。在数值模拟方面,何蕴龙等[4]进行了大量的有限元计算,总结了地震作用下边坡动力系数的分布规律,并提出了一个近似计算方法。冯志仁等[5]、陈臻林等[6]运用FLAC3D 进行数值模拟,分析了地震作用下含软弱夹层顺层和反倾边坡的动力响应特性。在振动台模型试验方面,许强等[7-12]通过大量的振动台模型试验,研究了地震作用下含水平软弱夹层斜坡和含反倾软弱夹层斜坡的动力响应特性和变形破坏特征。杨国香等[13-14]通过振动台模型试验,研究了地震作用下顺层边坡和反倾层状边坡的动力响应特性及破坏过程。
综上所述,针对地震作用下边坡动力响应特性及变形破坏过程已取得了较多的研究成果,但对于地震作用下含缓倾软弱夹层边坡的动力响应特性、变形破坏方式及失稳机理还有待进一步研究。为此,本研究通过FLAC3D 进行数值模拟,分析了地震作用下含软弱夹层边坡动力响应特性,并对边坡的稳定性进行拟静力分析,推导出考虑地震惯性力作用的边坡安全系数表达式,通过求解多元函数的方向导数,分析得出边坡最易失稳的位置,再通过动态强度折减法再现边坡渐进失稳过程,最终揭示边坡的失稳模式与破坏机理,为含软弱夹层矿山边坡的灾害防治提供依据。
1 边坡动力分析数值模型的建立
1.1 边坡模型及参数
根据含软弱夹层石灰石矿山边坡现场工程地质资料,建立含软弱夹层边坡概化模型,如图1所示。模型的高度为120 m,边坡的高度为100 m,下伏地层的厚度为20 m,模型底部的总长273.91 m,模型顶部的宽度为170 m,边坡的直线坡度为50°。阴影部分为软弱夹层,其他部分为石灰岩,软弱夹层在坡面上的临空点距坡底面的垂直距离为20 m,软弱夹层的倾角为20°、厚度为5 m(计算其他模型时相应地改变软弱夹层的厚度)。计算时的坐标原点选取坡底距左边界80 m 处,A1~A16为监测点,用来监测边坡各点的动力响应加速度值。
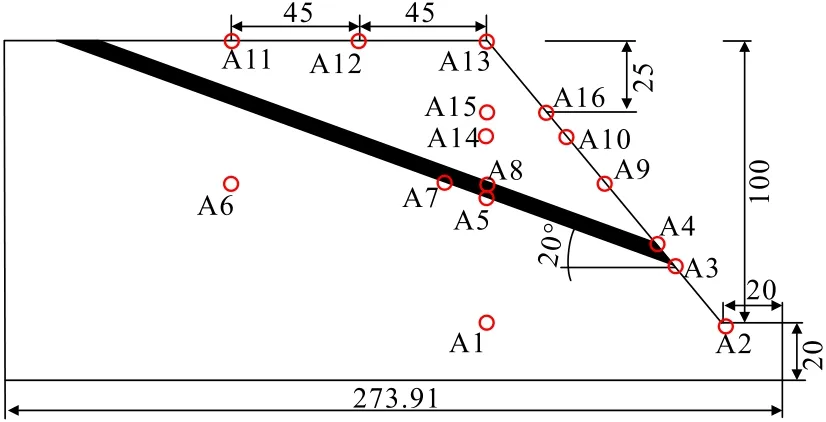
图1 含软弱夹层边坡计算模型(单位:m)Fig.1 Calculation model of slope with weak interlayer
本研究计算使用的模型材料岩体力学参数选自黄山石灰石矿,如表1所示。选用自由场边界条件和局部阻尼进行求解[15]。
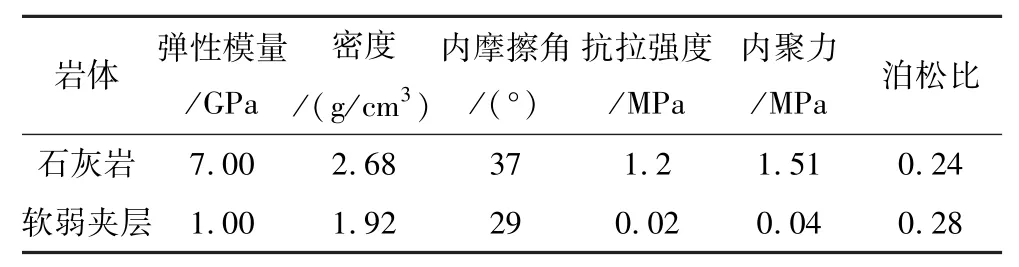
表1 岩体与软弱夹层物理力学参数Table 1 Physical and mechanical parameters of rock mass and weak interlayer
1.2 地震波的输入
本次数值模拟以汶川地震中监测到的实际地震波的节选部分为输入地震波,在水平方向和竖直方向上分别作用于模型底部,其加速度峰值为0.3g,持续作用时间为12 s,加速度时程如图2所示。计算过程分为两步,第一步是在重力的作用下生成初始应力,第二步再进行动力计算。
图2 地震波时程曲线Fig.2 Seismic wave time history curve
2 模型边坡加速度动力响应特性
地震通过地震惯性力对边坡稳定性产生影响,而地震惯性力的大小取决于加速度的大小,因此加速度是边坡动力问题分析的核心参数,故采用分析加速度的变化规律的方法来反映出边坡的动力响应特性。为了便于分析,引入加速度放大系数这一概念,定义为边坡各测点与坡底加速度峰值的比值。
2.1 水平加速度动力响应特性
图3为边坡模型在地震波峰值为0.3g的汶川波水平作用下,含不同厚度软弱夹层边坡的水平向加速度放大系数在坡面、坡内沿高程方向和坡内水平方向上的变化曲线。
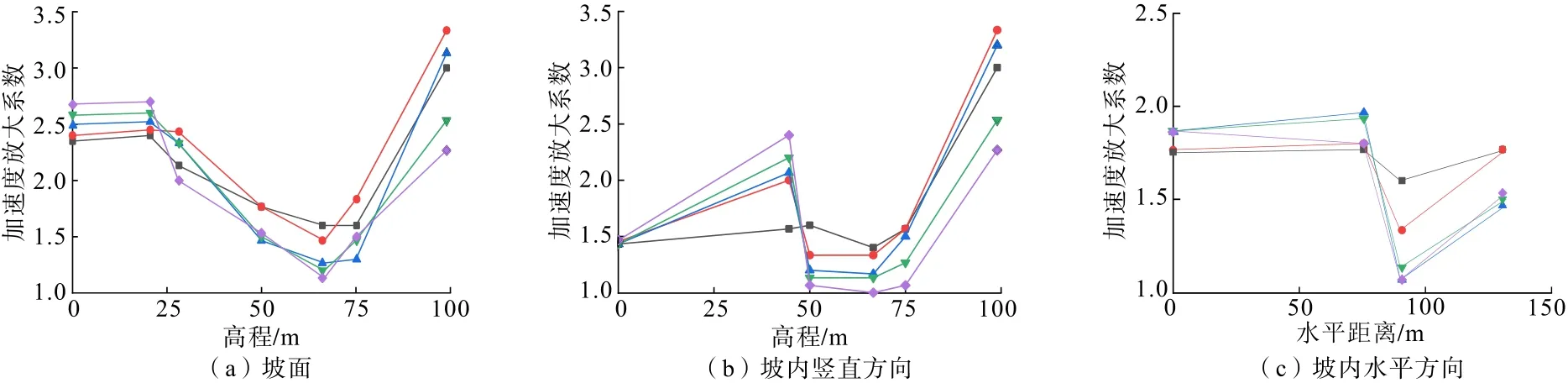
图3 水平加速度放大系数变化曲线Fig.3 Amplification coefficient variation curves of horizontal acceleration
从图3(a)中可以看出,坡面上,随着高程的增加,水平加速度放大系数整体上表现出先减小后增大的趋势,从坡脚到2/3 坡高处,水平加速度放大系数先基本保持不变,后呈现出非线性下降的特征,在3/4 坡高以上,加速度放大系数迅速增大,表现出明显的高程放大效应。在坡内竖直方向上,如图3(b)所示,从坡底到软弱夹层下表面,水平加速度放大系数缓慢增加,在经过软弱夹层后,加速度放大系数急速下降,在1/2 坡高处达到最小值,在1/2 坡高到3/4 坡高区域内,加速度放大系数略有起伏,但在总体上基本保持不变。从3/4 坡高往后,加速度放大系数迅速增大到最大值,这和坡面的变化规律相同,也表现出高程效应。在坡内水平方向上,如图3(c)所示,沿坡内指向坡外,水平加速度放大系数在很长一段距离上缓慢增加,增幅不大,经过软弱夹层后加速度放大系数大幅度下降,之后一直到坡表,加速度放大系数一直增加,表现出趋表效应。
2.2 竖直加速度动力响应特性
与水平加速度分析方法相同,图4为边坡模型在地震波峰值为0.3g的汶川波竖直作用下,含不同厚度软弱夹层边坡的竖直向加速度放大系数在坡面、坡内沿高程方向和坡内水平方向上的变化曲线。
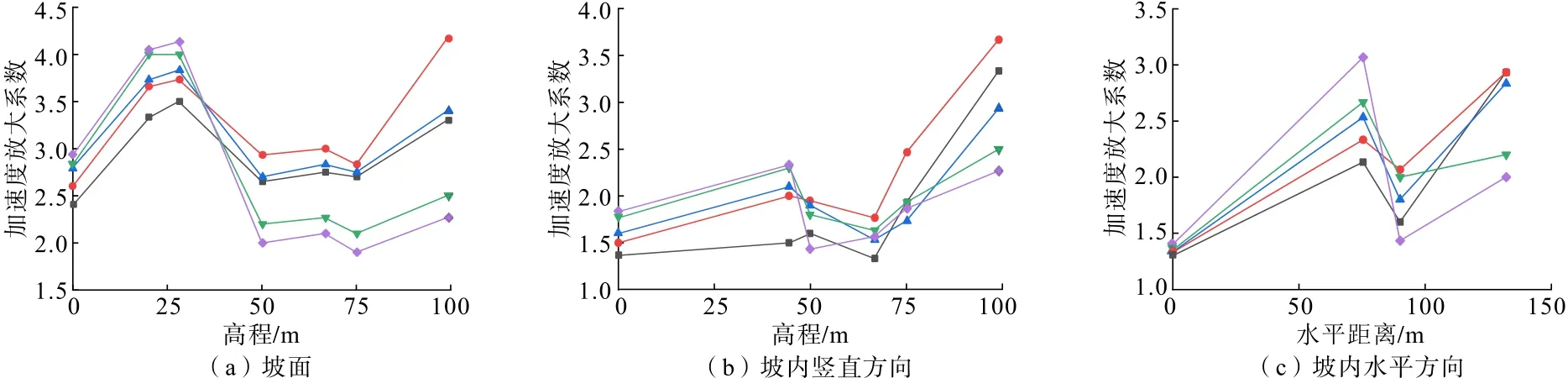
图4 竖直加速度放大系数变化曲线Fig.4 Amplification coefficient variation curves of vertical acceleration
从图4(a)中可以看出,坡面上,与水平加速度的动力响应特性有所不同,从坡脚至软弱夹层下表面,竖直加速度放大系数上升迅速,在经过软弱夹层后加速度放大系数略有减小,从软弱夹层上表面至1/2 坡高处,加速度放大系数迅速下降,在1/2 坡高到3/4坡高区域内,加速度放大系数略有减小。从3/4 坡高上至坡肩处,加速度放大系数迅速增大,表现出高程放大效应。在坡内沿高程方向上,如图4(b)所示,与水平加速度放大系数的变化规律大致相同,也是从坡底处增大到软弱夹层底部,经软弱夹层后开始下降,再从3/4 坡高之后迅速上升。不同的是,相较于水平加速度而言,经软弱夹层后,竖直加速度放大系数只有小幅度下降,远没有水平加速度削弱的幅度大。如图4(c)所示,在坡内水平方向上,竖直加速度的变化规律与水平加速度大致相同。
2.3 软弱夹层对边坡动力响应的影响
结合图3和图4 可知,软弱夹层的存在及其厚度对边坡模型动力加速度的整体变化趋势没有太大的影响,但对边坡局部位置的动力加速度放大系数以及边坡各位置加速度数值有较大的影响。相较于无软弱夹层边坡,软弱夹层以下,含软弱夹层边坡的加速度放大系数明显高于无软弱夹层边坡,并且软弱夹层的厚度越大,软弱夹层以下部位的加速度放大系数越大;而在软弱夹层以上,软弱夹层对边坡加速度的影响随着软弱夹层的厚度变化出现2 种不同的情况,薄软弱夹层(软弱夹层厚度为2.5、5 m)对边坡整体的加速度起到一定的促进作用,厚软弱夹层(软弱夹层厚度为7.5、10 m)对边坡整体的加速度则是起抑制作用,随着软弱夹层厚度的增大,边坡软弱夹层以上部位的加速度放大系数逐渐减小。软弱夹层附近的加速度普遍高于边坡其他位置,并且软弱夹层的厚度越大,软弱夹层附近的加速度越大。
边坡加速度最大值出现的位置亦受软弱夹层的影响,无软弱夹层边坡模型的水平和竖直加速度最大的部位均在坡肩处。薄软弱夹层边坡加速度最大值出现在坡肩处,厚软弱夹层边坡加速度最大值出现在软弱夹层与坡面的交界处。
3 地震作用下含软弱夹层边坡变形破坏分析
3.1 边坡稳定性拟静力分析
目前,拟静力法是分析地震边坡稳定性的常用方法,拟静力法的实质是在极限平衡法的思想上再考虑地震作用力对边坡稳定性的影响,也就是将随时间不断变化的地震惯性力当成是一个静力荷载作用在边坡体上的一种近似计算方法。自Terzaghi 首次运用拟静力的方法分析边坡动力稳定性问题以来,因其方法简便实用,至今仍然广泛应用到地震边坡问题分析之中。
本研究采用极限平衡法中适用于任何滑动面的普遍条分法[16](Janbu 法)为基础进行拟静力分析。在竖直条分法中,将地震作用力以水平地震惯性力和竖向地震惯性力的形式作用在条块的质心上,其大小分别为水平动力加速度和竖向动力加速度与条块重度的乘积。任取一条块i进行受力分析,如图5所示。
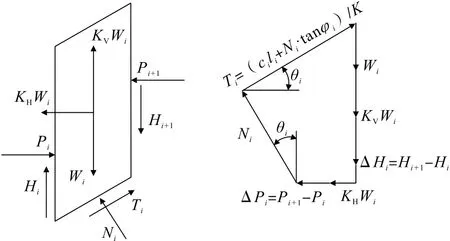
图5 简布法条块作用力分析Fig.5 Force analysis of strip by simple distribution method
根据库伦准则和极限平衡条件,并假定条块之间的剪切力之差ΔH=0,最终得到边坡安全系数K的表达式如下:
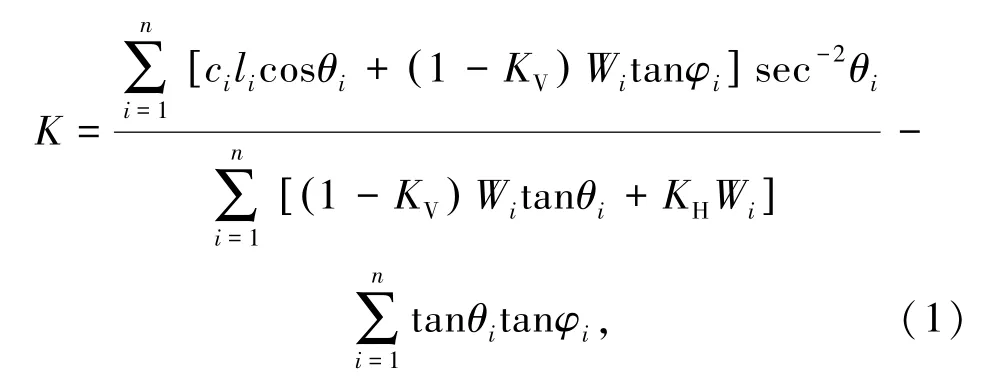
式中,K为安全系数;ci、φi、Wi分别为条块i的黏聚力、内摩擦角和重力;KH、KV分别为水平和竖向加速度系数。
对于一个确定的边坡来说,除了KH和KV是未知量以外其余量均为定值,因此可将边坡安全系数K看成一个关于KH和KV的二元函数。下面分析边坡安全系数K随KH和KV的变化规律。
令a=cilicosθi + Witanφi、b = Witanφi、c =Witanθi,d =tanθitanφi、KV=x、KHWi =y。简化函数并省略掉常系数sec-2θi,式(1)可简化为
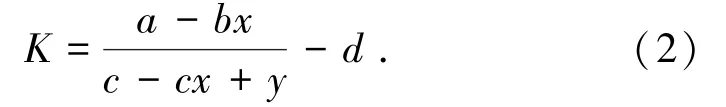
由式(2)可知:x不变时,K随y的增大而减小;y不变时,K随x的增大而增大,即在水平地震惯性力指向坡外、竖向地震惯性力竖直向下的情况下,边坡安全系数随着水平地震惯性力的增大而减小、随着竖向地震惯性力的增大而增大。虽然竖直向下的地震惯性力能够增大边坡的安全系数有利于边坡的稳定,但是地震是一个动态的过程,作用于边坡的地震惯性力的大小和方向随时间而不断变化,其中出现的竖直向上的地震惯性力则不利于边坡的稳定。
改变竖向地震惯性力的方向,此时水平、竖向地震惯性力单独作用于边坡时皆不利于边坡的稳定,探究水平、竖向地震惯性力共同作用下安全系数K随水平、竖向地震惯性力的变化规律。安全系数K的二元函数变为
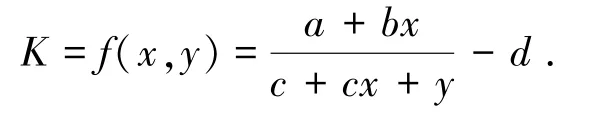
计算f在点(0,0)沿射线el=(cosα,cosβ)的方向导数,并判断其在该方向上的单调性。
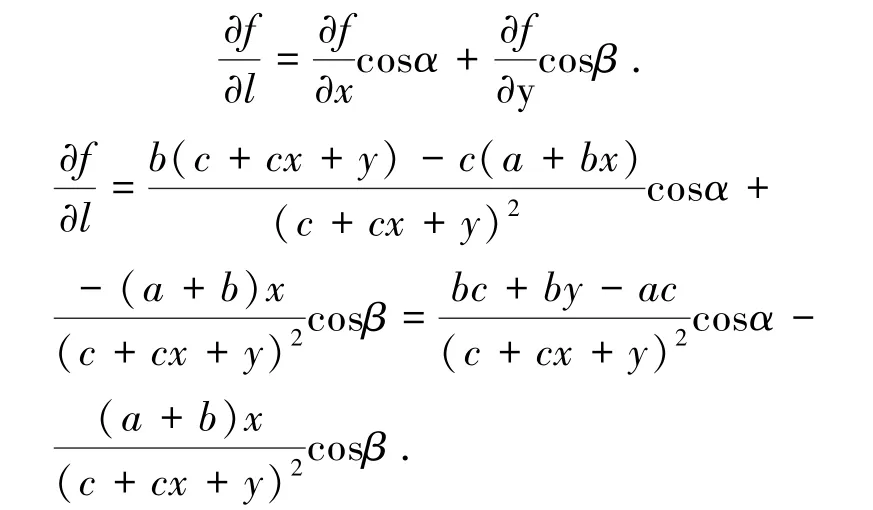
根据大量的地震现场实测记录,竖直地震动峰值与水平地震动峰值的比值P为1/2 ~2/3[17],当P=1/2 时,y=2x,射线,射线上另外一点(1,2)。在点(0,0)处:
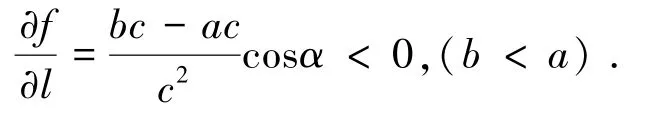
当x∈ [0,1] ,y ∈ [0,2] 时:
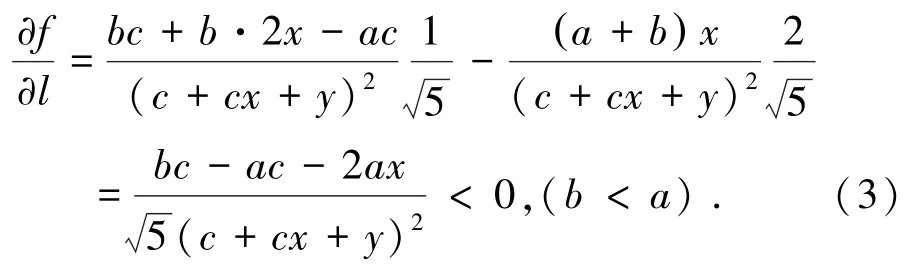
3.2 边坡失稳模式与破坏机理分析
上文分析了地震作用下含软弱夹层边坡加速度动力响应特性,薄软弱夹层边坡加速度最大值出现在坡肩,厚软弱夹层边坡加速度最大值出现在软弱夹层与坡面的交界处,在坡体中上部靠近坡面处,水平和竖直加速度被显著放大,即这些地方的地震惯性力较大。又由拟静力分析得出了安全系数K随水平、竖向地震惯性力的增大而减小,因此软弱夹层以上、坡体中上部靠近坡面处是最易失稳的地方。软弱夹层是边坡内部的薄弱环节,因其力学强度低、抗变形能力差,常成为潜在的滑移面。图6为地震作用下边坡的位移云图,可以看出,地震作用后边坡位移量较大的部位主要在软弱夹层上部、边坡的外部,软弱夹层与坡面交界处的位移最为明显,位移量不明显的边坡内部与位移量明显的边坡外部的分界线近似一条竖直线。

图6 边坡位移云图Fig.6 Cloud map of slope displacement
图7为不同折减系数下边坡塑性区分布图。由图7 可知,边坡首先在软弱夹层处产生剪切破坏,在软弱夹层的上部出现小范围的拉裂破坏,随着折减系数的增大,塑性区不断向坡顶扩展,直至塑性区贯通,边坡发生滑动。由以上分析可推断出地震作用下含软弱夹层边坡的失稳模式,边坡前缘位置沿软弱夹层发生层间平面滑动,以此带动边坡后缘形成拉裂破坏。
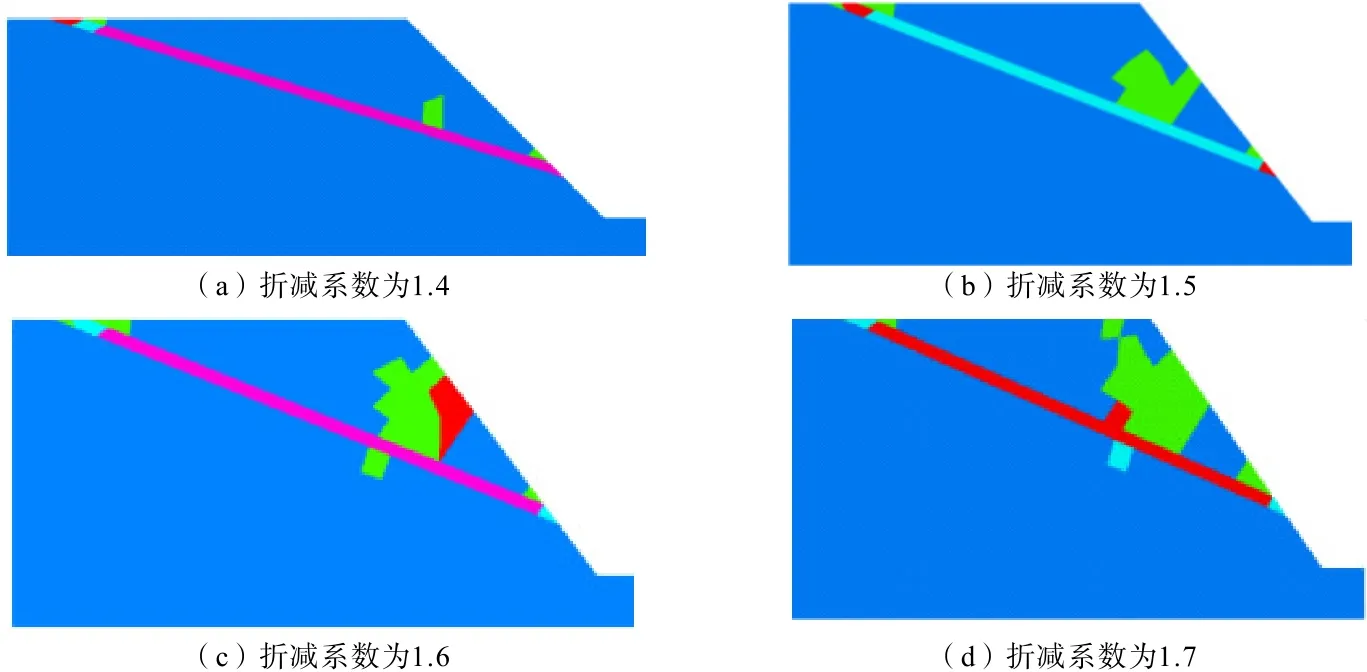
图7 边坡塑性区分布Fig.7 Plastic division layout of slope
软弱夹层对地震波的传播规律造成了较大的影响。根据弹性波散射理论,地震应力波在传播过程中遇到异质界面时,为了保持状态平衡,将发生波场分裂现象,主要表现为在自由表面的反射、坡内不连续界面(层面)的反射和折射,各种类型的波相互叠加在界面附近形成复杂的地震波场,这是软弱夹层影响边坡动力响应特性的主要原因。地震波从坡底传播到坡顶途径软弱夹层,经历了从硬岩到软岩、再从软岩到硬岩的过程,地震波发生了2 次反射和折射,由许强等[7]的研究,地震波从软岩向硬岩传播时发生的反射和折射要比从硬岩向软岩发生的反射和折射强得多。地震波在软弱夹层上表面、从软岩传播到硬岩的过程中发生了强烈的反射和折射现象,在软弱夹层附近形成了复杂的地震波场,使得边坡中软弱夹层附近的地震加速度值普遍高于边坡其他位置,这是地震造成含软弱夹层边坡失稳的内在原因。
4 结 论
(1)随着高程的增加,坡面上水平加速度先减小后增大,竖直加速度先增大后减小最后再增大;坡体内部竖直方向上,水平和竖直加速度均是先增大后减小最后再增大。在坡体中上部,水平和竖直加速度迅速增大,表现出明显的高程放大效应。在坡体内水平方向上,坡面处的加速度大于坡体内部,表现出趋表效应。
(2)相较于无软弱夹层边坡,薄软弱夹层对边坡整体的动力响应起到促进作用;厚软弱夹层表现出了隔震作用,对边坡动力响应起到削弱作用,并且软弱夹层厚度越大,对边坡动力加速度削弱得越明显。薄软弱夹层边坡加速度最大值出现在坡肩处,厚软弱夹层边坡加速度最大值出现在软弱夹层与坡面的交界处。
(3)通过拟静力分析方法得出,地震作用下边坡安全系数随水平、竖向地震惯性力的增大而减小,软弱夹层以上、坡体中上部靠近坡面处是最易失稳的地方。
(4)含软弱夹层边坡在地震作用的失稳模式为“沿软弱夹层发生层间平面滑动—拉裂破坏”。软弱夹层使地震波发生反射和折射,是影响边坡动力响应特性的主要原因,也是边坡失稳的内在原因。

