基于ADE-Stacking的心力衰竭非计划性再入院风险预测模型
王 磊,宋 波
(青岛科技大学信息科学技术学院,山东 青岛 266000)
0 引 言
随着我国人口老龄化加剧,心血管类慢性疾病的发病率不断升高,作为各种心脏疾病进展的终末阶段的心力衰竭(以下简称心衰)患病率也呈持续上升趋势[1-3],心衰患者中约有1/3的患者在出院后短期内再次非计划性入院[4]。非计划性再入院(以下简称再入院)一般是指患者诊疗流程结束后在一定时间内再次因同一疾病紧急入院[5],作为医疗质量评价指标一定程度上反映了住院期间的治疗效果[6]。心衰患者居高不下的再入院率不仅降低了患者的生存质量,同时还提高了患者的经济负担和社会的医疗成本[7-8]。有研究表明针对再入院风险较高的心衰患者,在住院期间采取干预措施可以使心衰患者再次入院的风险降低11%~28%[9-12]。所以,患者住院期间准确、高效评估患者的再入院风险,既是采取针对性治疗护理的前提,也是降低再入院率的关键。
传统再入院评估模型医院得分[13]和LACE索引[14]是美国医疗机构中使用最广泛的再入院风险计算模型,但这类模型依靠实践经验进行人工定义,效果取决于经验总结是否准确,存在较大的局限性[15]。随着近年来大数据挖掘与机器学习技术的发展,为评估心衰患者再入院风险问题提供了更新更有效的技术手段。文献[16]在国内率先提出了再入院问题的机器学习预测方法,将逻辑回归、随机森林和支持向量机3种分类器分别应用于同一再入院数据集,通过对比分析发现,随机森林算法在再入院风险预测问题中具有更高的准确率。文献[17]使用FCM(模糊C均值聚类算法)解决了再入院患者占总体患者比例较小的数据不均衡问题,并构建了一种采用贝叶斯模型进行超参数优化的梯度提升决策树预测模型,在糖尿病再入院风险评价中取得了较高的预测准确度。文献[18]构建了基于神经网络、随机森林和支持向量机算法的3大类共10个再入院风险评估模型,对真实再入院数据集进行对比实验后发现,支持向量机模型在使用多项式为核函数时表现出最优的预测准确率。文献[19]使用高斯过程模型(GPM)和超声心动图参数建立风险预测模型,较好地预测了慢性左室收缩功能减低(LVSD)的心衰患者一年内再入院风险。
本文旨在提升心衰患者再入院风险预测的准确率,使用Stacking集成学习算法构建风险预测模型,并提出改进差分进化算法(Adaptive DE)对Stacking算法中分类器的参数进行寻优,构建基于ADE-Stacking的再入院风险预测模型。
1 基于ADE-Stacking的再入院预测模型
本文结合ADE与集成学习Stacking算法构建再入院预测模型,模型框架如图1所示。模型主要由2部分构成,分别为左侧的ADE算法与右侧的Stacking算法。在算法流程中首先ADE算法进行参数初始化,生成初始种群,然后对种群中的每个个体进行变异操作与交叉操作,交叉操作后会分别得到原始个体与新个体2组待优化参数。Stacking算法通过参数初始化后将数据集10折划分,随后在每1折数据集上使用ADE传递的2组待优化参数进行模型训练,训练完成后测试并计算评价指标,直至10折交叉验证完毕后,分别将2组待优化参数对应的测试评价指标均值传递给ADE,由选择算子挑选出较优的个体(即一组待优化参数)保留至下一次迭代过程,直到ADE达到最大迭代次数,输出模型的最优参数。

图1 ADE-Stacking模型框架
2 Stacking集成学习算法
Stacking中文为堆叠之意,该方法使用异质弱学习器,采用层次融合的思想,利用元模型对弱学习器进行组合[20]。Stacking模型作为一种新颖的集成学习策略,相较于传统的bagging和boosting模型,拥有更加优异的性能[21]。
Stacking模型主要包括2层,第1层由N个异质弱学习器构成。首先将数据集分为训练集与测试集,并划分训练集为K折,其中1/K作为训练时的检验集。然后依次使用每个弱学习器进行K次训练,每次训练完成后对检验集与测试集进行预测,每一个弱学习器训练完成后将K次检验集的预测结果进行拼接,作为下一层的输入。
第2层将第1层各个弱学习器的检验集预测结果与样本真实类别标签作为输入,建立元模型进行训练,最后将第1层各个弱学习器在测试集上的结果取均值输入元模型,此时元模型的输出即为最终预测类别或概率。Stacking结构如图2所示。

图2 Stacking模型框架
3 改进差分进化算法
3.1 差分进化算法
差分进化算法(Differential Evolution, DE)由Storn与Price所提出,是一种基于模拟群体中个体的合作与竞争过程的进化算法,具有收敛速度快、控制参数少、鲁棒性强等优点[22]。在算法中,个体的基因表示待求解问题的一个候选解,每次迭代过程都进行变异、交叉、选择操作,迭代完成后选取最优个体的基因作为解。标准差分优化算法流程如算法1所示。
算法1 标准差分优化算法
输入:M为种群规模,D为解向量维度,T为最大代数
输出:Δ为最优解向量
1:t←1(初始化)
2:fori=1 toMdo
3:forj=1 toDdo
5:end for
6:end for
7:while(|f(Δ)|≥ε) or (t≤T) do
8:fori=1 toMdo
9:变异与交叉
10:forj=1 toDdo
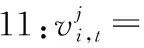

13:end for
14:选择
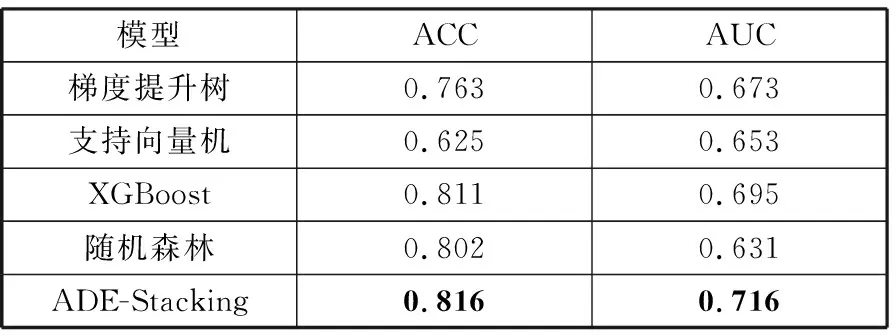
15:iff(ui,t) 16:xi,t←ui,t 17:iff(xi,t) 18:Δ←xi,t 19:end if 20:else 21:xi,t←xi,t 22:end if 23:end for 24:t←t+1 25:end while 26:return最优解向量Δ 3.1.1 种群初始化 (1) 3.1.2 变异算子 变异算子是差分演化算子中最为重要的一个,也是差分进化算法区别其他进化算法的重要因素。假设当前个体为xi,在标准差分进化算法的变异操作中,首先从父代中任意选取3个互不相同的个体x1、x2、x3,且x1不等于x2不等于x3不等于xi,然后x2与x3进行差运算得到差分向量后通过缩放因子F对差分向量进行缩放,最后缩放后的差分向量与x1进行和运算得到新的个体vi。如式(2)所示: vi=x1+F×(x2-x3) (2) 3.1.3 交叉算子 交叉算子的作用是将当前个体的部分分量与变异个体的对应分量按规则进行交叉以获得一个新的个体,以常见的二项式交叉规则为例,首先对个体向量的每一维都产生一个0到1之间的随机数randj,然后分别将每一维的随机数与交叉率CR进行比较,若随机数小于CR,则新个体对应维度来自变异个体,否则来自当前个体。如式(3)所示: (3) 3.1.4 选择算子 选择算子通过适应度评价函数,从当前个体与交叉之后的新个体中选择更优的个体作为下一次迭代种群中的个体。如式(4)所示: (4) 差分进化算法虽然最优解特性保持良好,自适应性强,空间复杂度较低且性能优异,但对参数的设置较为敏感[23]。从算法流程中不难看出,算法中个体在搜索空间中的变化步长由收缩因子F控制,对种群多样性和收敛性有很大影响,F较大时,种群中个体的扰动较大,全局搜索能力较强,但收敛速度较慢;F较小时,步长减小,局部勘探能力增强且收敛较快,但易陷入局部最优。与标准差分进化算法中收缩因子F为一个0到2的常数不同,本文提出自适应收缩因子F,依据算法迭代次数自适应改变,以增强算法初期的全局探索能力和后期的局部勘探能力。 自适应收缩因子设计如式(5)所示: (5) 其中,t为当前代数,T为最大代数。收缩因子F无需外部输入,而是根据迭代次数从2到0自适应减小。收缩因子在算法初始时取值为F=2,使算法具有较大变异率,从而增加种群多样性与全局探索能力。探索进入后期,随着迭代次数t增加,逐渐趋近于T,收缩因子F的值逐渐减小,算法的局部探索能力增强并快速收敛。 为了验证与分析ADE在寻找全局最优解问题中的优势与特点,分别使用ADE与DE算法对Rastrigin函数进行寻优,如式(6)所示: (6) 函数图像如图3所示,已知Rastrigin函数的最优解为f(0,0,…,0)=0。首先,对2种算法设置相同的操作参数,群体规模M=20,解的维度D=2,迭代次数T=150,解空间为[-100,100],交叉参数CR=0.8。DE中收缩因子F依次取值为0.2、0.4、0.6、0.8、1.0、1.2、1.4、1.6、1.8、2.0。DE的收缩因子F的每次取值,分别使用ADE算法与DE算法进行10次寻优,并记录寻优过程中取得最优解的次数。结果如图4所示。 图3 Rastrigin函数图像 图4 ADE与DE算法寻优结果 由图4易知,ADE算法在50次寻优中只有4次未寻得最优解,求得全局最优解的比率为92%,DE算法在收缩因子F取值不同时,求得全局最优解表现存在较大差异,在收缩因子F=0.4、0.6、0.8、1.0、1.2时表现较好,在取其他值时表现较差。通过对比,ADE算法较DE算法有更好的最优解求解能力和鲁棒性,且无需外部输入参数收缩因子F。 本文使用青岛某三甲医院心内科心力衰竭病人数据集,用于验证本文所提出的心力衰竭再入院风险预测模型。该数据集包含心衰患者基本信息、体征信息、检查数据以及再入院情况4类信息共计20个维度,每个维度的特征如表1所示。 表1 数据集特征表 数据集无缺省值,所以无需考虑进行缺省值处理,但在接下来的模型训练过程中,为消除指标之间量纲不同对数据分析产生的影响,需要对数据进行标准化处理,通过标准化使各指标处于同一数量级,可以帮助模型更快收敛至最优解。本文采取最常用的min-max标准化数据规范方法,如式(7)所示: (7) 其中,k=1,2,…,d,xi(k)代表第i个样本的第k维特征值。 本文所提出的模型中超参数优化算法ADE较标准DE算法,仅需要外部提供4个参数,无需设置参数收缩因子F。Stacking模型第一层梯度提升树、支持向量机、XGBoost、随机森林4个算法共需提供8个参数的上下界,第二层由XGBoost作为元模型需提供3个参数上下界,需要ADE优化的参数共计11个。具体参数设置如表2所示。 表2 参数设置 本文采用准确率(ACC)与受试者工作特征曲线下面积(AUC)作为评价指标。分别使用ADE-Stacking模型与Stacking中的梯度提升树、支持向量机、XGBoost、随机森林在数据集上进行20次10折交叉验证,评价指标取20次实验平均值。从表3中的实验结果容易获知,本文构建的基于ADE-Stacking再入院风险预测模型具有更高的准确率和受试者工作特征曲线下面积。 表3 各算法模型准确率 心力衰竭的非计划性再入院问题不仅反映了医院的诊疗质量,而且浪费了宝贵的医疗资源,提高了社会医疗成本,加重了医保负担。本文通过对再入院问题进行研究提出了ADE-Stacking再入院风险预测模型,能够有效判断患者再入院风险,帮助医护执行更有效、更有针对性的诊疗与护理,以避免心衰患者非计划性再入院。本文工作主要概括为以下2点。 1)使用集成学习Stacking算法构建心力衰竭患者再入院风险预测模型,通过集成各个弱分类器优点,提高模型对再入院风险预测的拟合能力。 2)针对集成学习算法中诸多弱分类器的参数调优问题,提出使用差分进化算法对集成学习模型中的参数进行优化,并在标准差分进化算法基础上进行了改进,提出自适应缩放因子F以提高寻优能力。 此外,本文仍然存在一定的局限性,因未能收集到其他疾病的有效数据集,无法测试本文提出的算法在应对其他病种的再入院问题是否能够保持较高的准确率与性能。希望后续能够与医院加强合作,获取更多更有效的数据以支持再入院风险预测问题的研究。
3.2 差分进化算法自适应缩放因子
3.3 自适应收缩因子差分进化算法性能分析


4 再入院风险预测实验
4.1 数据处理
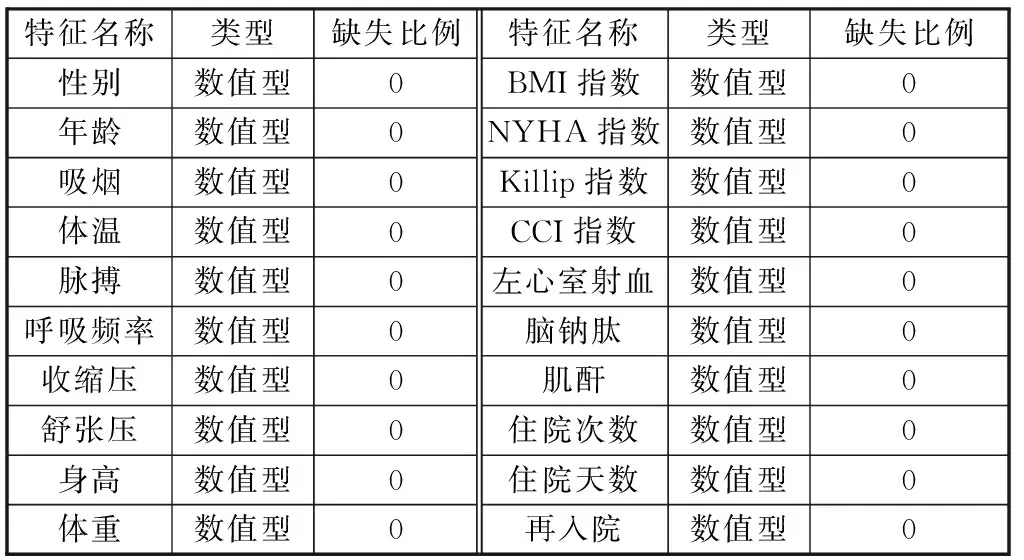
4.2 实验参数设置

4.3 结果与分析
5 结束语

