基于ABAQUS的管内密封胶筒性能参数优化

张 康，吴 凯

(1.大连海事大学，辽宁 大连 116026; 2. 浙江大学，杭州 310058)

随着海底管道使用年限的增加，以及外部复杂环境的影响，海底管道极易形成腐蚀、破裂、变形以及泄露等缺陷，严重的会导致管道安全事故，造成经济损失，还会威胁海洋环境安全。因此，针对海底管道事故快速处置的管道应急维抢修技术应运而生。在海底管道应急维抢修技术中，管内智能封堵技术[1-2]由于其简单、方便、快捷等优势，逐渐得到了越来越广泛的应用。管内智能封堵技术的核心是管内高压封堵能力，而密封胶筒是决定装置封堵能力的关键部件，其性能参数直接决定管内封堵的效果。因此，对于管内密封胶筒密封性能[3-4]的研究是管内封堵技术研究中的主要问题之一。 对于封隔器密封胶筒的研究[5-10]已经比较成熟，通过建立封隔器胶筒力学模型，结合有限元分析软件，模拟封隔器密封胶筒坐封过程，并对胶筒密封过程进行变形以及受力分析，进而得到更加合理的胶筒参数。对于橡胶密封能力的设计以及优化，也有一些学者应用有限元仿真分析软件[11-12]，针对大变形的密封胶筒进行了密封性能分析以及参数优化[13-15]。

目前对于密封胶筒性能的研究主要集中在封隔器上，而管内封堵装置的密封胶筒与封隔器的密封元件无论在外形上还是在材料选择上都存在差异。因此，本文在前人的研究基础之上，针对特定研究工况，详细论述研究管内密封胶筒各个参数对封堵性能的影响。应用有限元仿真方法，并结合多参数耦合分析法，对密封胶筒硬度、高度、厚度、外倾角4个参数进行分析，并得到各个参数的最优解。本文的研究内容将为进一步提高管内封堵技术中的胶筒密封性能优化研究提供支撑。

1 胶筒力学模型建立

1.1 胶筒材料本构模型

本文的研究对象为密封胶筒，其组成材料是橡胶。橡胶是超弹性材料，在受到挤压时，会产生高度非线性的大变形，具有材料非线性的特性。在描述非线性材料力学行为的过程中，通常是通过张量函数来建立模型[7]。橡胶胶筒本构模型可用应变能函数W来描述，即W=W(I1，I2，I3)或W=W(λ1，λ2，λ3)。其中变形张量的3个主伸长比和3个不变量的关系如式(1)所示。

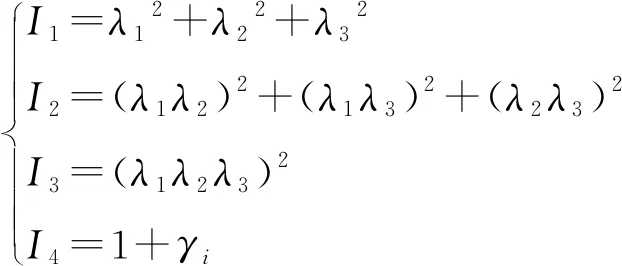
(1)

式中：I1，I2，I3为变形张量不变量；λ1，λ2，λ3为主伸长比；γi为主应变。

橡胶是不可压缩材料，且具有各向同性的特点。橡胶有很多本构模型，常用的有Mooney-Rivlin模型和Yeoh模型[9]。根据管内密封胶筒的预计变形量和工况，本文选择Mooney-Rivlin典型2参数模型进行模拟。应变能函数可化简为

W=C10(I1-3)+C01(I2-3)

(2)

式中：W为应变势能；C10、C01为Mooney-Rivlin常数。

弹性模量E与剪切模量G的关系为：E=3G，其中G=2(C01+C10)。对于密封胶筒，C01/C10=0.5,从而得到2个材料常数。此外,胶筒变形还存在几何非线性、接触非线性的特点。

1.2 胶筒变形阶段力学性能分析模型

管内密封胶筒在受到驱动力挤压后，先后发生自由变形与约束变形。在自由变形阶段，即，胶筒触及管壁之前。胶筒轴向受到来自封堵器的驱动力，径向发生弹性变形，且应力与应变呈线性关系。由广义胡克定律可以得到胶筒变形几何方程如式(3)。

(3)

式中：εr为径向应变;θ为周向应变;εz为轴向应变；σr为径向应力；σθ为周向应力；σz为轴向应力；ur为胶筒沿径向方向的变形；uz为胶筒沿轴向方向的变形。

进入约束变形阶段，胶筒的受力情况比较复杂，为了获得更准确的受力分析情况，决定采取有限元分析方法，从而保证接触应力有更小的误差。

2 密封胶筒仿真及单参数调节

通过前文对胶筒本构模型的选择、胶筒变形的受力分析可知，要获取密封胶筒与海底管道之间准确的接触应力，则必须要对整个封堵结构进行有限元分析。采取有限元的方法，模拟密封胶筒从受压变形到接触管壁的过程，提取出胶筒与管壁的接触应力，进而分析出胶筒的密封性能。本次仿真所使用的软件为ABAQUS，二维图形由CAXA电子图板绘制。

2.1 仿真过程

2.1.1 胶筒模型简化

智能封堵器密封模块构件众多，并且海底管道内壁由于长期承受内部液体的高压作用而形成凸凹不平的表面，这使得胶筒接触变形的条件变得很复杂。同时也给非线性的有限元分析收敛性计算带来了许多困难。为了便于求解，同时使得计算结果更为准确、可靠，应对胶筒模型进行适当的简化。

密封模块由底座、上挤压碗、下挤压碗、胶筒以及海底管道组成，如图1所示。并且密封模块的三维模型是轴对称的，其所受载荷、约束也是轴对称的。所以，在有限元分析的过程中可以把胶筒模型简化为二维的，这样就简便了计算过程，在满足计算精度的同时大幅提高模拟计算效率。

2.1.2 边界条件施加

在有限元分析过程中，边界条件的施加也尤为重要，应尽可能地还原出实际工况中的载荷和约束情况。ABAQUS模拟的过程是上挤压碗受到来自封堵器的驱动力作用而向下运动，挤压胶筒变形，使胶筒贴近海底管道管壁，达到封堵的效果。由此可以得到：

1) 约束方面。

底座、下挤压碗与海底管道皆为钢制结构，结构稳定性良好。在智能封堵器工作过程中，这3个构件均起到支撑的作用。底座、下挤压碗与海底管道产生的径向(x轴方向)变形较小，可以忽略不计。所以，在胶筒简化的二维模型中，将底座、下挤压碗与海底管道的约束设置为：在x轴方向施加变形ux=0，在y轴方向施加变形uy=0。上挤压碗因摩擦力所引起的径向变形可忽略不计，故其边界条件设置为：在x轴方向施加变形ux=0。

2) 载荷方面。

施加的外力载荷只有驱动力。本次仿真决定采用均布载荷的形式模拟此驱动力，即在上挤压碗上表面，设置均布载荷为10 MPa。边界条件施加情况如图1所示。

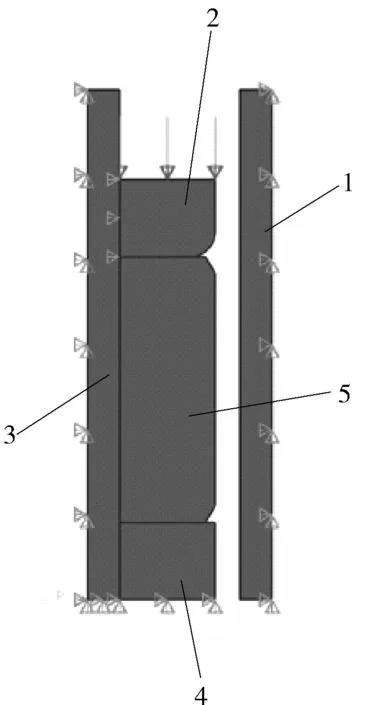
1-海底管道;2-上挤压碗;3-底座;4-下挤压碗;5-胶筒。

2.1.3 摩擦接触设置

在胶筒模型中，由于构件之间存在接触关系，需要考虑摩擦，因此需要对模型中发生接触行为的构件进行摩擦因数的定义。胶筒与管壁的接触类型是刚体-柔体的接触。管壁作为刚体，设置为主面；胶筒作为柔体，设置为从面。胶筒与管壁之间的切向摩擦可以简化为橡胶与钢的摩擦，摩擦因数定义为0.4。同理，胶筒与上、下挤压碗、底座之间的摩擦因数也定义为0.4。底座与挤压碗之间的切向摩擦因数可以简化为钢与钢的摩擦因数，定义为0.15。

在胶筒发生大变形的过程中，胶筒不仅与周围的构件相接触，还会发生自接触。自接触在接触条件设置时是很容易被忽略的1个环节，自接触的摩擦因数定义为0.5。

2.1.4 网格尺寸及单元属性的确定

密封胶筒是本文主要研究对象，且其发生的变形量较大，为了获取更精确的结果，应对胶筒的网格进行加密处理。但网格不是越密越好，当网格数量较少时，提升网格密度，会使计算精度显著提高；当网格数量增加到一定程度时，再提升网格密度，计算精度只有极少量的提高，反而会大幅增加计算时间，不利于求解。因此，在对胶筒网格划分时，要进行网格无关性分析。

密封胶筒采用四节点、双线性轴对称四边形单元，即CAX4RH单元。其余构件采用四结点双线性轴对称四边形单元，即CAX4R单元。本文选取的3个网格尺寸分别为1.5、1.2、1.0，模拟计算出的胶筒变性后与管道之间形成的最大接触应力分别为10.060、9.895、9.868 MPa。由此可以得出，当网格尺寸从1.5提高到1.2时，接触应力有较为明显的变化。当网格尺寸从1.2提高到1.0时，接触应力变化很小，误差小于3%，说明网格尺寸为1.2时计算结果已经达到精度要求。但是，由于网格尺寸的提高成倍地增加了计算时间，大幅降低求解效率，因此本文选定的网格尺寸为1.2。

2.2 仿真结果

经过仿真计算，胶筒的变形及最大接触应力发生处如图2所示。

通过依次选择海底管道内管壁上的节点，提取这条路径上的应力值，绘制图3。从图3中可以看出，胶筒与管壁之间的接触应力基本呈线性分布，在此计算工况以及驱动力的作用下，其最大接触应力为5.1 MPa。

图2 胶筒变形云图

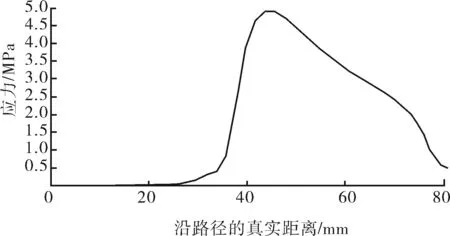
图3 海底管道内管壁应力分布

2.3 胶筒参数调节

在密封胶筒仿真计算的基础上，采取控制变量的方法，研究胶筒不同参数对管内胶筒密封性能的影响。原始参数的胶筒二维模型如图4所示。β为胶筒外倾角。

图4 胶筒二维模型

1) 胶筒硬度。

橡胶材料的硬度一般为60～90 IRHD。橡胶是不可压缩材料，泊松比μ近似取为0.48。不同硬度的橡胶对应弹性模量也不同，所得Mooney-Rivlin模型的2参数C10、C01也不同。根据ABAQUS中不可压缩系数d的定义：d=(1-2μ)/(C01+C10)可得不同硬度的不可压缩系数。如表1所示。

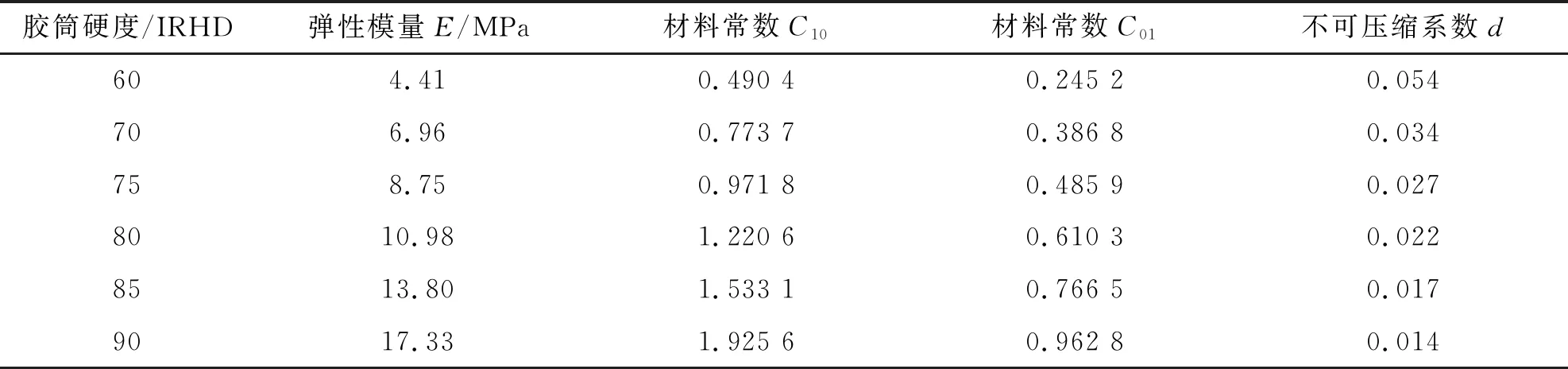
表1 胶筒橡胶材料参数

分析结果如图5所示。当其他因素不变时，胶筒硬度越大，封堵时产生的接触应力越小，越难以达到封堵要求。当胶筒硬度为60 IRHD时，接触应力最大，达到了5.014 MPa。其中施加的均布载荷为10 MPa。

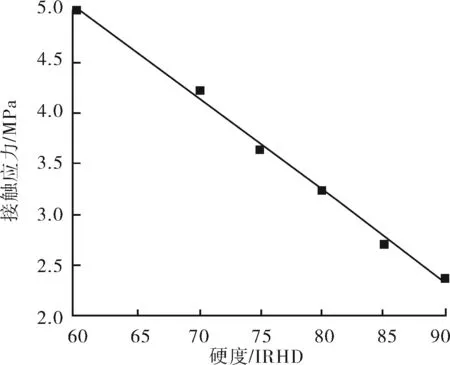
图5 胶筒硬度对接触应力的影响

2) 胶筒厚度。

在胶筒外倾角为30°、均布载荷为10 MPa的条件下，取胶筒厚度为设计变量。胶筒厚度从23 mm变化到25 mm，每隔0.5 mm依次变化。由仿真结果可知，随着胶筒厚度的增加，胶筒与管壁之间的接触应力越大。当胶筒厚度为25 mm时，胶筒与管壁之间的接触应力最大，为5.277 MPa。如图6所示。

3) 胶筒高度。

在胶筒外倾角为30°、均布载荷为10 MPa的条件下，取胶筒高度为设计变量。胶筒高度从35 mm变化到85 mm，每隔10 mm变化1次。由仿真结果可知，随着胶筒高度的增加，胶筒与管壁之间的接触应力越大，但增速趋缓。当胶筒高度为85 mm时，胶筒与管壁之间的接触应力最大，为5.266 MPa。可根据需要选择合适的胶筒高度，不必过度追求胶筒高度，胶筒高度过高会导致结构稳定性较差。如图7所示。

图6 胶筒厚度对接触应力的影响

图7 胶筒高度对接触应力的影响

4) 胶筒外倾角。

胶筒外倾角为胶筒二维模型右侧的倒角(与铅垂方向夹角，铅垂方向长度为4 mm)。胶筒的外倾角一般为30～60°，每隔5°变化1次。由仿真结果可知，胶筒外倾角的改变对胶筒与管壁之间的接触应力的影响不大，上下浮动区间约为0.2 MPa。其中接触应力达到最大时，胶筒外倾角为30°。当其他条件相同时，若想获得更好的封堵性能，则需选择外倾角为30°的胶筒。如图8所示。

图8 胶筒外倾角对接触应力的影响

3 多参数耦合优化

3.1 拟合过程

在单参数分析的基础上，将不同参数拟合分析，探究在多参数复合影响下，接触应力的变化特性，并得到最优参数配置。本次拟合采用的软件为Design-Expert 8.0.6。拟合方法为响应面分析法[16-18]，此方法的本质是使用多项式近似隐式极限状态函数。

首先将硬度、高度、厚度、外倾角设为自变量，接触应力设为因变量。设置自变量的变化范围：硬度60～90 IRHD、高度30～85 mm、厚度23～25 mm、外倾角30～60°。软件自动分配出29试验组参数，试验数据如表2所示。

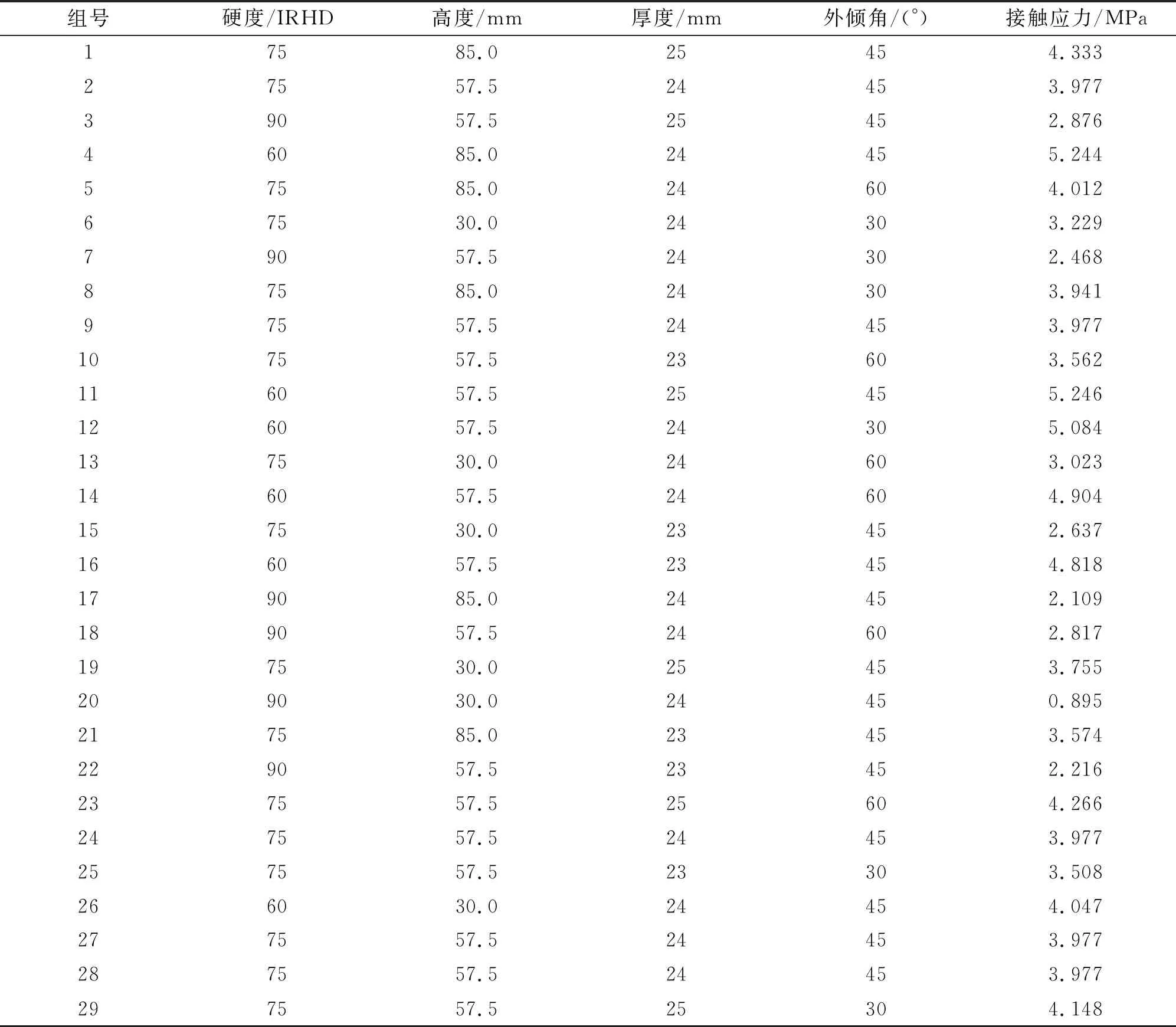
表2 响应面分析试验数据组

3.2 拟合结果

1) 硬度与高度。

胶筒硬度与高度的耦合作用如图9所示。胶筒硬度对接触应力的影响较大，随着硬度的增加，接触应力越来越小。

图9 硬度与高度耦合作用

2) 硬度与厚度。

胶筒硬度与厚度的耦合作用如图10所示。由图10可以看出，在胶筒厚度单参数影响之下，随着胶筒厚度的增加，接触应力不断增大，这与前文中对胶筒单参数的分析结果相符合。

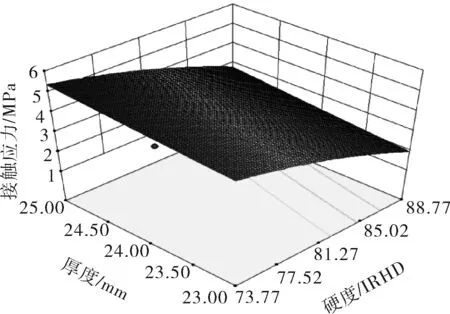
图10 胶筒硬度与厚度的耦合作用

3) 硬度与外倾角。

胶筒硬度与厚度的耦合作用如图11所示。外倾角对接触应力的影响不大。

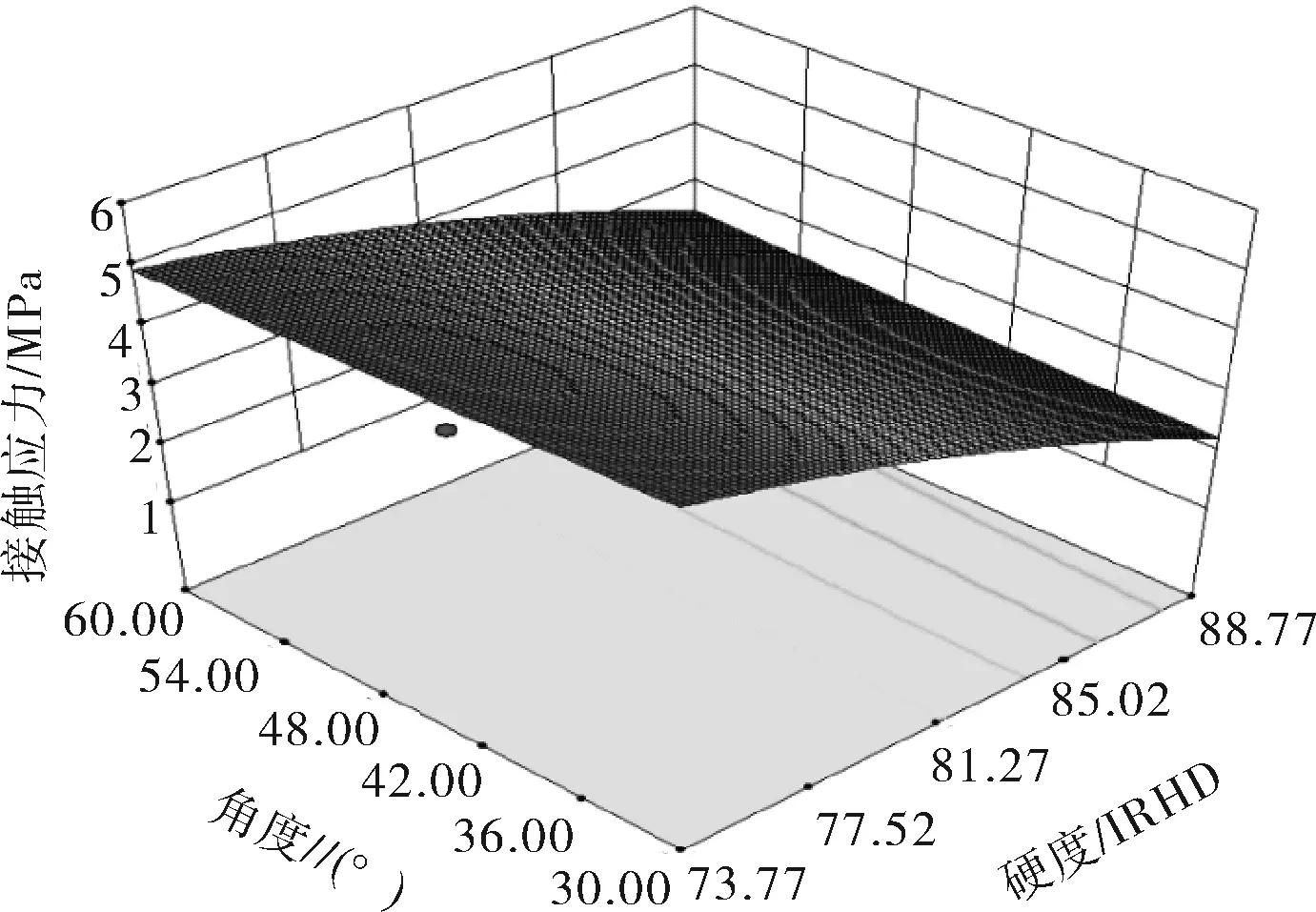
图11 胶筒硬度与外倾角的耦合作用

4) 高度与厚度。

胶筒高度与厚度的耦合作用如图12所示。此三维图上接触应力最大值发生在曲面上，而并非发生在沿着胶筒高度、厚度2个因素坐标轴走向的最大值，因此可以说明，接触应力受到胶筒高度、厚度2个因素交互影响。

图12 胶筒高度与厚度的耦合作用

5) 高度与外倾角。

胶筒高度与外倾角的耦合作用如图13所示。随着高度的增加，接触应力不断增大。

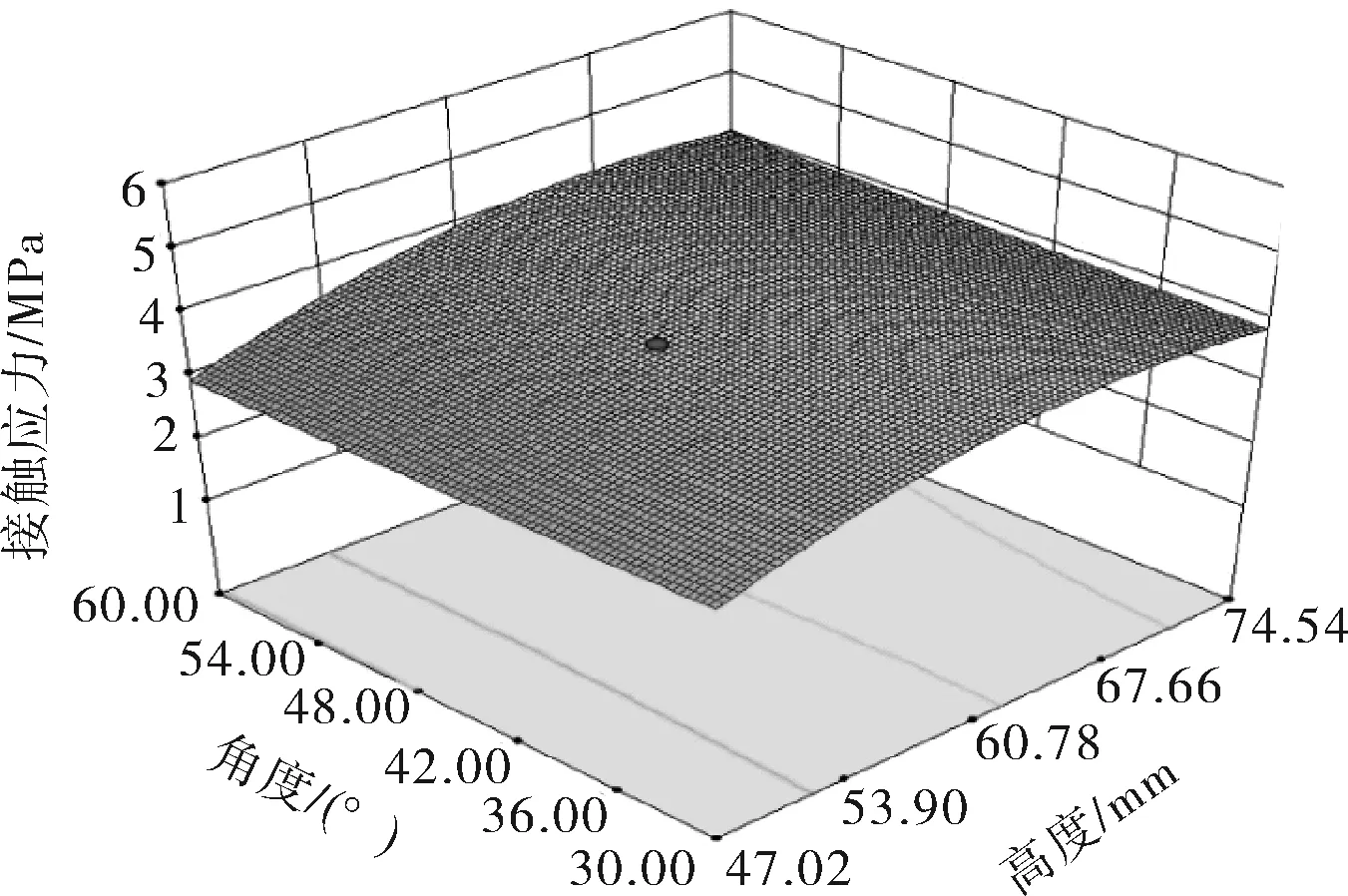
图13 胶筒高度与外倾角的耦合作用

6) 厚度与外倾角。

胶筒厚度与外倾角的耦合作用如图14所示。从图14中可以看出厚度对接触应力的影响不大。

图14 胶筒厚度与外倾角的耦合作用

7) 综合分析。

综上所述，通过采用响应面分析法对胶筒的多参数耦合作用进行了分析，利用多元二次回归方程可以得到针对此工况下的管内密封胶筒封堵能力最优参数组合。各参数最优组合如表3所示。

表3 胶筒参数优化结果

4 结论

1) 本文开展了管内封堵装置密封胶筒的有限元分析。通过胶筒密封模型简化、边界条件施加、摩擦接触设置、网格划分及单元确定等，实现了管内胶筒密封过程模拟分析，并得到密封过程与管壁之间的接触应力变化特性。

2) 针对特定工况，应用有限元分析方法，系统完整地分析了管内密封胶筒各个参数对其密封过程与管壁之间的接触应力的影响，并且得到了单参数与胶筒密封性能之间的特性关系。

3) 结合多参数耦合分析方法，应用响应面分析法以及多元二次回归方法，拟合分析密封胶筒的各个参数对于胶筒密封性能的耦合影响特性。通过分析，得到各参数在此特定工况下的最优组合解，实现了管内密封胶筒密封特性最优化。为解决管内封堵装置胶筒密封性能优化问题提供了新的思路。