喷砂工艺的EDEM-Fluent耦合模拟喷嘴结构参数的研究

周大鹏，马学东，杜昱霖，张凡，陈燕，王海令

喷砂工艺的EDEM-Fluent耦合模拟喷嘴结构参数的研究

周大鹏1，马学东1，杜昱霖1，张凡1，陈燕1，王海令2

（1.辽宁科技大学 机械工程与自动化学院，辽宁 鞍山 114051；2.鞍山市长和冶金设备制造有限公司，辽宁 鞍山 114031）

研究在喷砂工艺过程中，喷嘴的收缩角、喉部半径及扩散角3种结构对出砂平均速度和出砂总量的影响规律及原因。利用EDEM-Fluent耦合模型，对喷砂喷嘴内气固两相的运动状态进行模拟，并通过实验验证其正确性。以喷嘴的不同结构大小设置正交表进行仿真实验，运用方差分析法（检验），分析各因素水平出砂平均速度和出砂总量的变化规律，并利用控制变量法，进一步探究喉部半径对出砂平均速度和出砂总量的影响原因。由出砂平均速度方差分析可得，喉部半径的值为3716.044，收缩角的值为380.102，出砂平均速度随着喉部半径的增大而快速增大，随着收缩角的增大而减小。由出砂总量方差分析可得，喉部半径的值为103.695，收缩角的值为13.101，出砂总量随喉部半径的增大而快速减小，随着收缩角的增大而缓慢增大。当收缩角和扩散角不变的情况下，随着喉部半径增大，喷嘴内负压增大，导致气相流速增大，进而使出砂平均速度增大。随着喉部半径增大到8 mm时，出砂平均速度不再增大，且有略微下降，其峰值为184.65 m/s。在砂粒生成速率相同的情况下，得出喉部半径越大，砂粒速度越大，砂粒在喷嘴内的停留时间越短，收缩段待喷出的砂粒质量越少，且分布状态越稀疏。验证了EDEM-Fluent耦合模拟喷嘴内气固两相流场是合理可行的。基于这一仿真模型，得出了出砂平均速度及出砂总量分别与喷嘴不同结构参数之间的关系规律，其中喉部半径对两者的影响最为显著。随着喉部半径越大，出砂平均速度越大，单位时间内在喷嘴出口处统计到的砂粒总量越少。

喷嘴结构；EDEM-Fluent耦合；出砂平均速度；出砂总量；方差分析；检验

喷砂工艺在多个领域的运用越来越广泛，比如航空、船舶、医药等领域机械构件的表面处理[1-2]。喷砂的功能是可以有效地去除其表面的氧化皮、锈斑、残漆等污染物，使其表面可以获得一定的清洁度[3-4]，还可以改变材料表面的粗糙度和力学性能，为一些热喷涂表面进行预处理[5-7]。砂料主要是通过压缩空气得到动力，以高速射流的形式喷到需要处理的工件表面，使工件外表面发生质的变化[8-9]。其中，喷嘴是喷砂机作业的重要元件，虽然喷嘴成本低，结构简单，却能获得超音速气相流场，进而影响出砂速度和出砂量，这两者是喷砂作业效率和良好工件质量的重要影响因素。因此，研究喷嘴结构具有重要的现实意义。

正因为喷嘴在磨料气体喷射中的独特作用，国内外学者对其已有了一定的研究。如李钦奉[10]利用喷砂实验方式建立了喷嘴半径与用砂量相互关系式。Liu等[11]对用于破碎岩石磨料气体射流的喷嘴结构，采用Fluent数值模拟和室内实验验证相结合的方法，研究了不同收缩角、喉部拉伸比、扩散角对板件冲蚀速率的影响，并优化出为磨料加速的最佳喷嘴结构。曹玮[12]通过Fluent对砂粒在喷嘴内的气体流场进行仿真模拟，得到砂粒粒径、收缩角与砂粒最大总动量相互之间的关系。殷硕等[13]采用CFD模拟喷嘴外部流场，并进行数值分析，得到了喷嘴不同出口直径对粒子冲击速度及基板最佳位置的影响规律。Ju等[14]通过欧拉-欧拉有限元软件获得激光熔覆过程中三维同轴送粉喷嘴内的双流体模型，来研究喷嘴结构参数对粉末颗粒流动的影响，并建立了优化喷嘴结构的数学模型。江竹亭等[15]运用有限元法对多孔陶瓷快速成形喷嘴内的三维流场进行了研究，通过VOF分析了直角型、收缩型和扩张型喷嘴结构对速度、压力分布和泥料体积分数的影响。Peng等[16]通过Fluent软件对冷冻机中的V型喷嘴进行了模拟，为了得到较大的出口速度，研究了不同喷嘴结构参数对出口速度的影响。刘雪梅等[17]以拉格朗日和欧拉法相结合的方式仿真模拟了喷丸工艺过程，得到了入口压强、粒径、粒子流量等参数与出口粒子速度的相互关系，再以喷丸时间和比能优选出了一组最佳的工艺参数。由此看出，现有对喷嘴方面的研究，要么是不够全面系统，要么是偏重于喷嘴内部气固流场自身运动特性的讨论，却少有以出砂平均速度和出砂总量为目标，来探讨喷嘴不同结构具体作用规律的系统性研究。另外，可以发现，大多数学者的研究与仿真软件结合得相当普遍，然而数值分析工具的运用较为单一。虽然单独的使用有限元软件也能够达到部分研究的目的，但由于软件自身的局限性，表现出的不足之处是将气固两相看成了混合流体，固体相被拟流体化，进而不能体现固体相的外形体积、碰撞以及位置等情况。为了能够弥补这一不足，使气固两相流场的模拟更趋于真实化、形象化，因此将有限元软件（Fluent）和离散元软件（EDEM）结合起来[18]，其耦合过程是一个瞬态双向数据传递的过程。这一方法目前普遍运用在输运管道[19]、流化床[20]、谷物风选[21]等领域的分析，然而，鲜有将这一耦合方法运用到喷砂工艺的研究中来。

综上所述，现以三维文丘里型喷嘴为研究对象，采用EDEM-Fluent耦合方法对喷嘴内气固两相瞬态流场进行数值模拟，并分析验证其合理性和可行性。对喷嘴的不同结构参数进行数值模拟，通过分析方法，研究喷嘴的收缩角、喉部半径和扩散角与出砂平均速度及出砂总量的相互关系，得出其影响规律。这一研究内容及方法在喷砂领域基本空白，研究结论对以后优化喷嘴设计，提高工作效率给予了理论支持。

1 设计方案

1.1 喷嘴结构设计

喷嘴作为喷砂工艺的核心部件之一[22]，采用最具有代表性的喷嘴文丘里型，如图1所示。为了能够在模拟仿真中达到对比效果，在改变喷嘴收缩角、喉部半径2、扩散角等参数的同时，选择了相同的入口半径和喷嘴的总长度。文丘里型喷嘴的几何参数见表1。

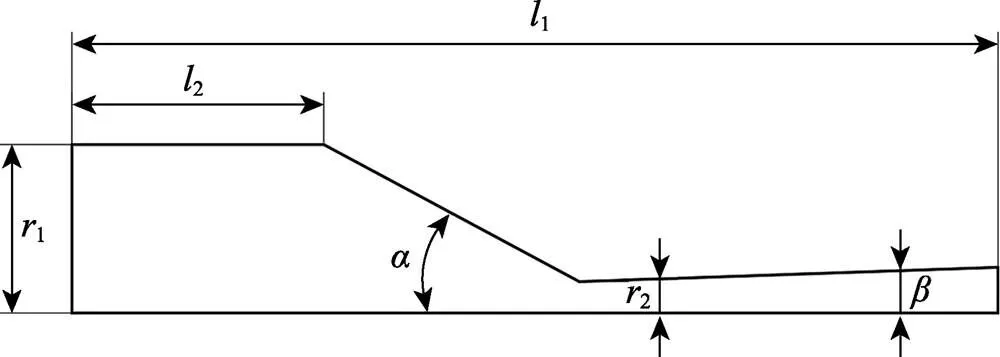
图1 文丘里型喷嘴几何结构

表1 文丘里型喷嘴几何参数

Tab.1 Venturi nozzle geometrical parameters

1.2 设计中心正交表

选取了文丘里型喷嘴的收缩角、喉部半径、扩散角3种结构参数作为重要的影响因素，并对不同因素的几何参数进行正交设计。然后对每组参数进行仿真分析，最后对统计出的结果进行方差分析。正交实验因素水平表见表2。

表2 因素水平表

Tab.2 Factor level table

为了避免人为编排因素水平表给仿真实验带来影响，因此采用SPSS设计中心正交表[23]。首先，假设各因素之间无相互作用，利用正交表安排进行9组仿真实验，方案见表3。

表3 正交实验方案

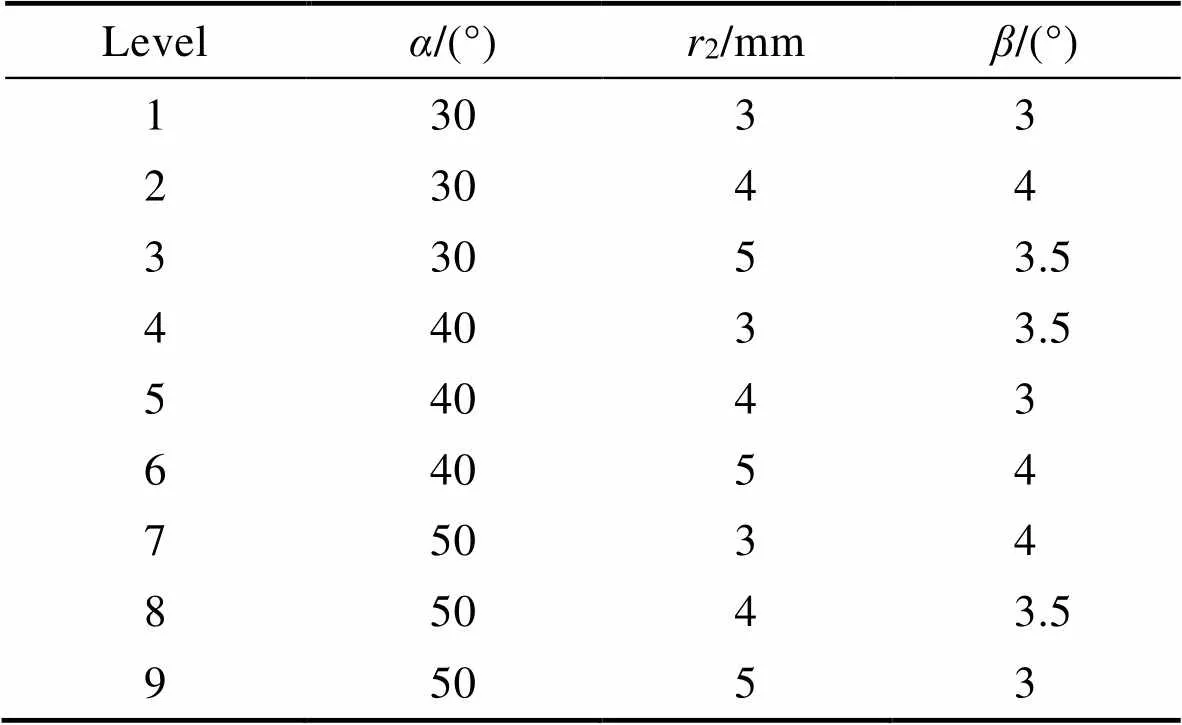
Tab.3 Orthogonal experiment scheme

2 数学理论模型

2.1 气相控制方程

在喷嘴模型内，将空气设为理想气体，忽略空隙率，以减少仿真时间，考虑曳力、重力，忽略萨夫曼升力、马格努斯效应等的影响，继而得到连续性方程、动量守恒方程及湍流方程[24-25]。

连续性方程：

动量守恒方程：

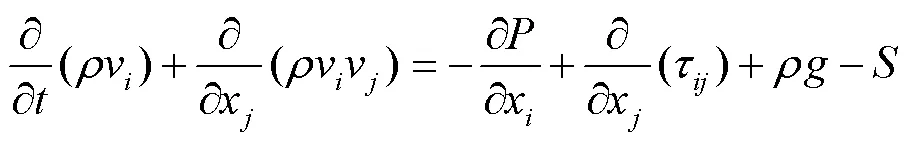
其中：

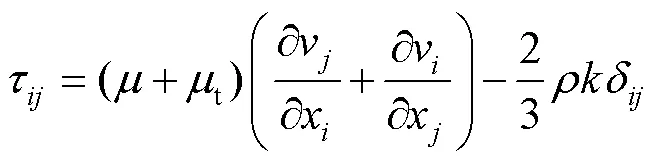
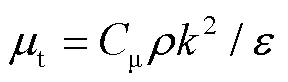
式中：、为坐标方向；ν、ν为气相速度；为气相压力；为气固相互作用项；为气相黏度系数；t为湍流黏度系数；δ为Kronecker数；μ为经验常数，取0.09。

气相在喷嘴内流速较快，流动雷诺数远大于4000，作湍流态，因此选择标准模型。其中，为湍流动能方程，如式（5）所示；为湍流耗散方程，如式（6）所示。

方程：

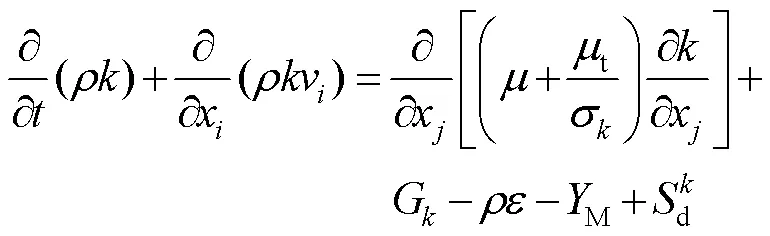
方程：

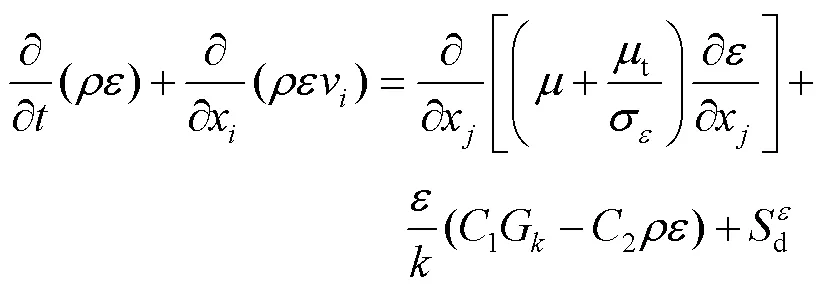
其中：

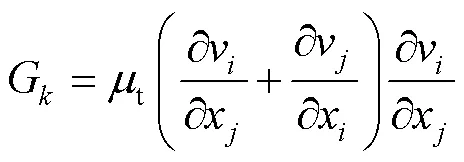
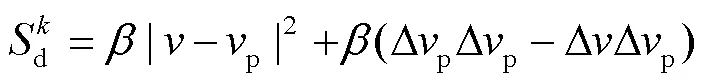
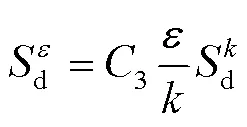
2.2 颗粒运动方程

EDEM中，为提高仿真速度，固体颗粒简化为球形。其次，因颗粒量较少，可忽略其体积分数。根据牛顿第二定律，单个固体颗粒在流体作用下的运动公式见式（10）、（11）[26]。

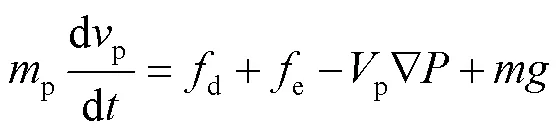
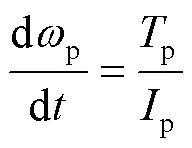
其中：

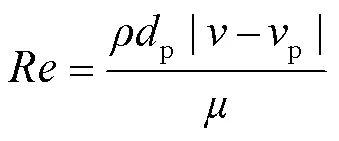
3 模拟仿真

3.1 有限元模型

首先，运用Soildwoks建立三维喷嘴模型，如图2所示。喷嘴进口面命名为Pressure-inlet，出口面命名为Pressure-outlet。在Fluent中，打开压力求解器Pressure- Based，设置喷嘴进口处压力为6×105Pa，出口处压力为1×105Pa（1个大气压），时间步长为8×10–5s。

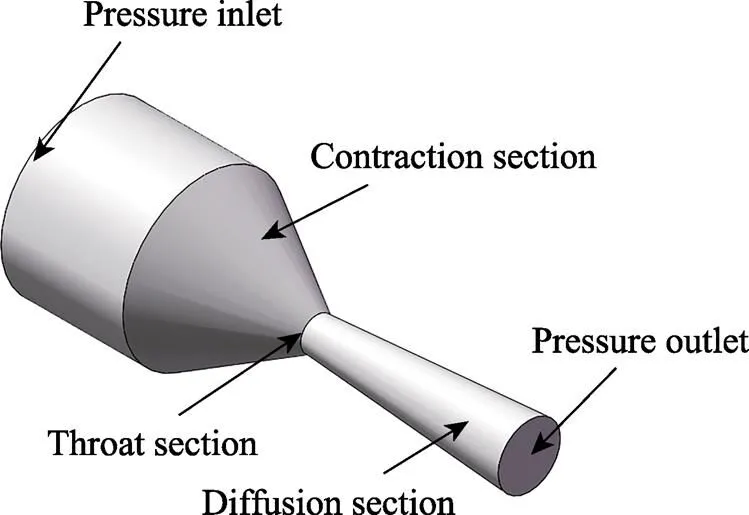
图2 喷嘴三维模型

3.2 离散元模型

EDEM中的参数设置：颗粒材料为石英砂，喷嘴材料为Steel，两者的材料属性见表4，接触模型系数见表5[27]。为了能够快速顺畅地生成颗粒，将颗粒工厂设置为半径18 mm、母线长为20 mm的圆柱体，颗粒半径为0.3 mm，生成速率为0.1 kg/s。环境（Envirnment）中设有重力，时间步长为8×10–7s，数据每0.01 s保存一次，仿真总时间为1 s。

表4 材料属性

Tab.4 Material properties

表5 材料接触系数

Tab.5 Material contact coefficient

3.3 模型分析

为了分析基于EDEM-Fluent耦合模拟仿真喷砂喷嘴的可行性，以收缩角为30°、喉部半径为4 mm、扩散角为4°的喷嘴为例，在Fluent中得到气相流场的压力云图和速度云图分别如图3a和图4a所示。喷嘴内压力分布形成的压力差是气体流动的必要条件。从图3b和图4b可以看出，进口段（0～30 mm）静压值基本稳定，气相流速也是如此；喷嘴收缩段到喉部的位置（30～60 mm），随着横截面积逐渐缩小，静压值由略微下降到快速降低，呈现出负压状态，使得气相流速在这一位置快速上升；到了喷嘴扩散段（60～110 mm），随着横截面积逐渐扩大，静压值缓慢增加，到达出口端时，接近外部大气压值，导致气相流速逐渐降低，符合实际工况下喷嘴内流体的状态，也满足砂粒喷射的要求。

图3 气相压力变化

图4 气相速度变化

上文分析了喷嘴中气相流体在Fluent中的合理性，接下来分析固体相颗粒在EDEM中的运动状态，如图5所示。从图5中可以看出，在气体流场的作用下，颗粒从收缩段喉部区域开始有明显的加速，在扩散段接近出口处，颗粒速度趋于稳定，符合真实情况下喷砂喷嘴中砂粒的运动状态。喷嘴的收缩段和出口处都设有长方体统计网格，其中，出口处的统计网格不仅能够统计出单位时间内喷嘴喷出砂粒的速度，还可以统计出总仿真时间内累计的出砂量，如图6a所示。在0.05～0.1 s，由于气流的不稳定，导致砂粒出口速度有些许波动；在0.1 s之后，砂粒出口速度基本上趋于稳定，说明喷嘴内砂粒运动状态良好。图6b中喷砂总量随时间的增加呈线性增长，说明喷砂均匀连续没有断层现象。

图5 0.06 s时砂粒在喷嘴中的运动

图6 EDEM中砂粒出口速度与出砂量随时间的变化

为了验证上述仿真模型所得结果的有效合理性，比较直观且科学的方法就是测量喷嘴出口处的砂粒速度，因此搭建了实验平台，将自制的砂粒测速装置放在喷砂室里，如7图所示。该装置由双盘测速法[28]制得，其工作原理如图8所示。首先使双盘同时旋转起来，并利用调速器将旋转速度设为恒定值，高速运动的砂粒穿过上圆盘的径向狭缝后，飞行距离（35 mm）后，击打在下圆盘上。下圆盘上覆有一张复写纸和白纸，砂粒击打会使白纸上留有痕迹，该痕迹与起始位置的偏转角度为砂粒穿过双盘之间运动时间的度量。利用其估测出喷砂速度，关系式如（14）所示。

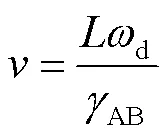
式中：v为出口砂粒速度；ωd为双圆盘转动角速度；γAB为圆盘狭缝沿径向边线与白纸上击打痕迹最远位置的夹角。

实验所用喷嘴为文丘里型喷嘴，其结构参数与上述数值模拟所用的喷嘴相同。首先，启动空压机，利用调压阀将喷嘴入口压力稳定在0.6 MPa，用过EI质量流量控制阀将砂粒流量控制在0.1 kg/s。然后打开喷砂测速器，利用调速器将转速控制在800 r/min。为了提高测量的准确性，在实验条件相同的情况下，共进行了4组实验，所得结果如图9所示。黑线A为狭缝沿径向的边线，视为起始位置，红线B为砂粒穿过狭缝在下圆盘上喷打痕迹的最远位置，两者的夹角为AB，其值分别为14.5°、14°、13.5°、15.5°。经式（14）计算可得，砂粒出口速度分别为115.86、120、124.44、108.39 m/s。可以看出，喷砂砂粒出口速度基本稳定，实验结果与上述仿真统计的结果也基本吻合，验证了其有效合理性。

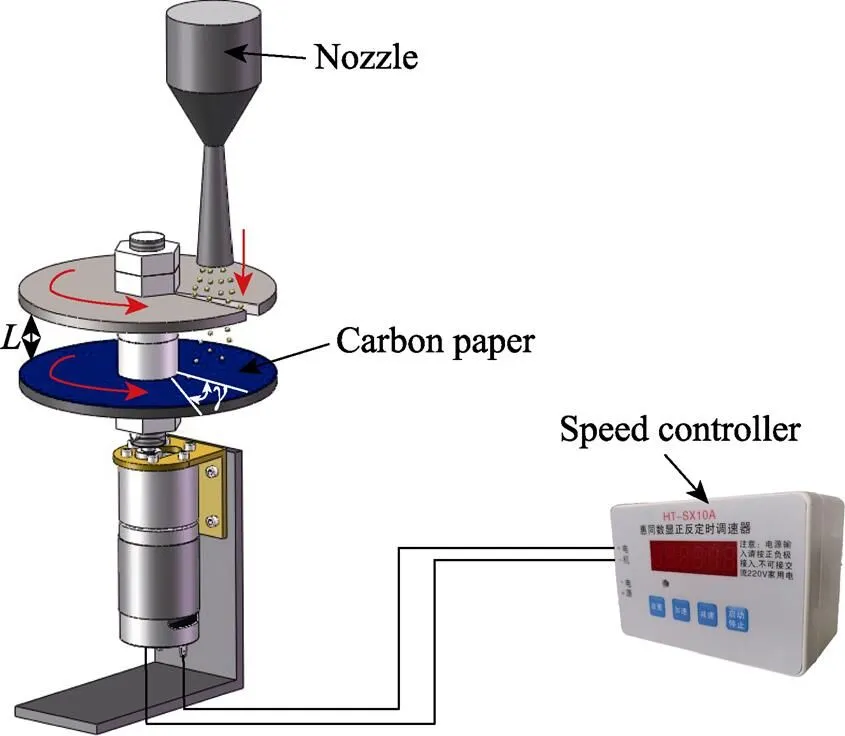
图8 喷砂测速器原理

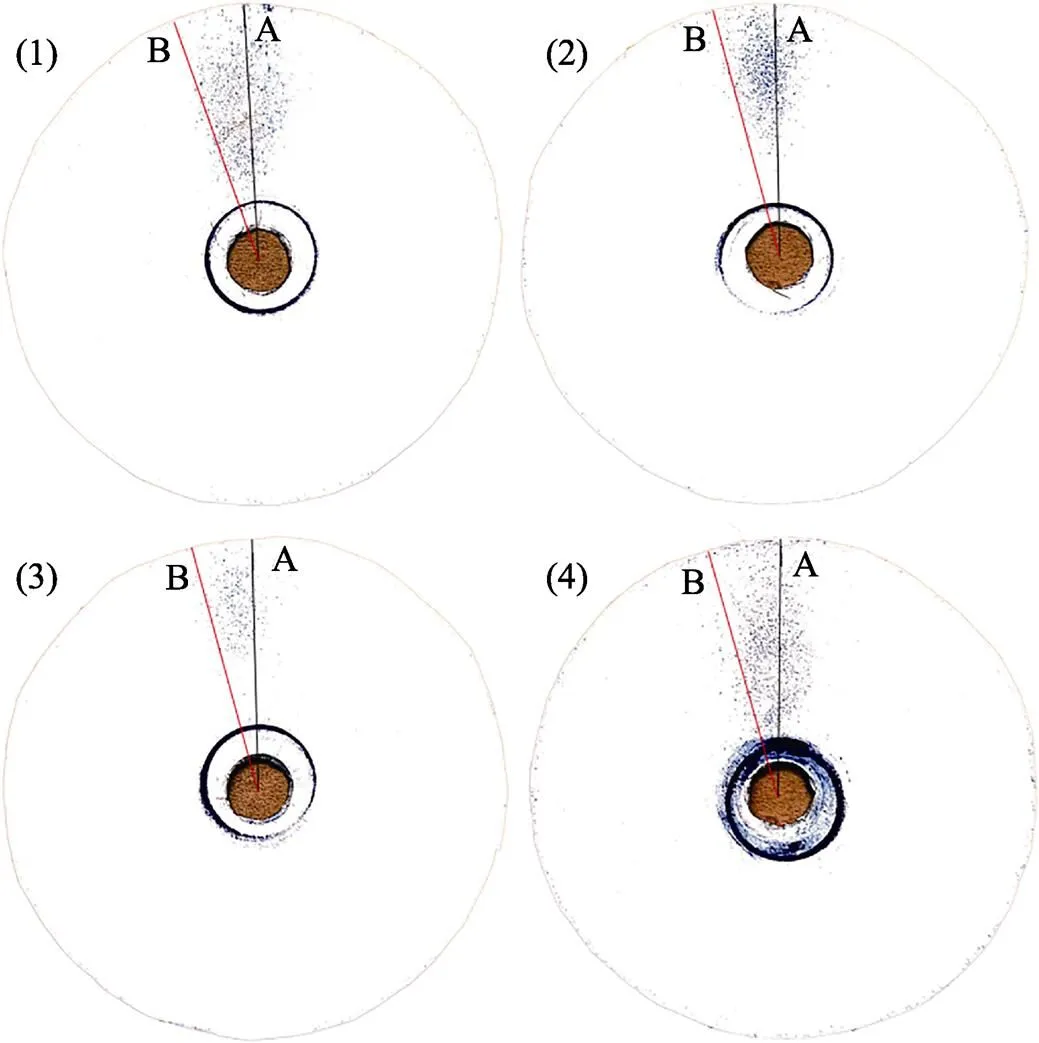
图9 实验结果

4 仿真结果与分析

在压强、颗粒粒径一定的情况下，选取了喷嘴的收缩角、喉部半径和扩散角为仿真参数变量，并建立了正交表，得到了不同参数组合下喷出砂粒的平均速度和总出砂量。为此，做了9组模拟仿真，仿真结果见表6。

表6 仿真结果

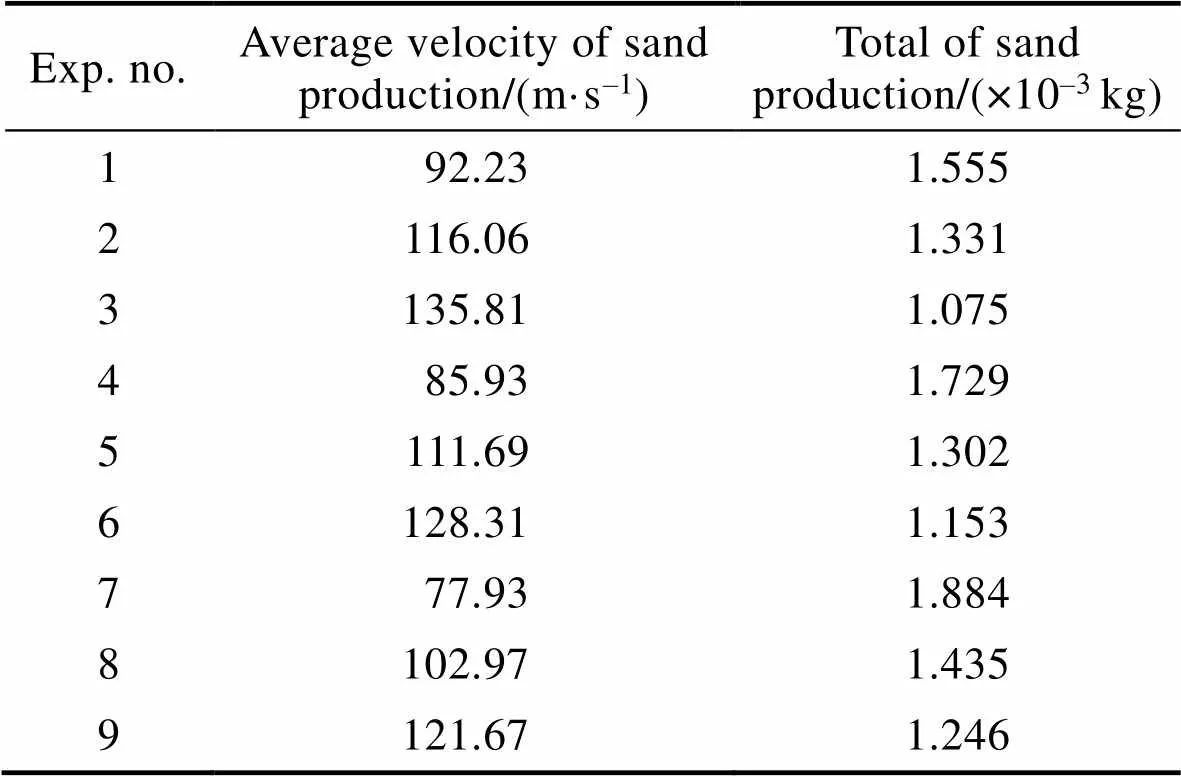
Tab.6 Simulation result

为了分析喷嘴的收缩角、喉部半径以及扩散角对出砂平均速度和出砂总量的影响，需要对自由喷砂仿真结果进行方差分析。方差分析的优势在于可以分辨出不同仿真实验结果的差异性。在方差分析中，各因素对实验结果的影响程度是否显著以值为判断标准[29]。首先，变差平方和计算公式为：

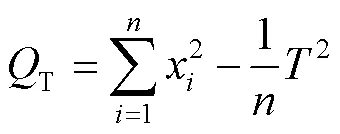
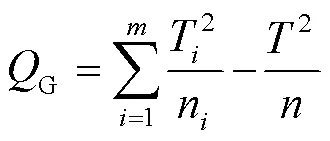
式中：T为仿真结果总变差平方和；G为因素效应变差平方和；为实验次数；为各水平的结果总和；为因素水平数；n为因素水平实验次数；T为因素水平实验结果的总和。

各因素的值公式为：

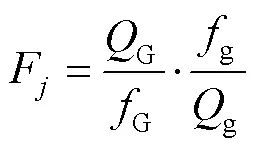
如果出现误差自由度较小，将导致误差偏大，检验灵敏度不高。为提高分析精度，将影响因素不显著的变差平方和自由度，分别合并到误差效应的变差平方和自由度中，重新计算显著因素的值，完成进一步比较。

利用EDEM软件中统计网格的方法，将喷嘴仿真时长1 s内的出砂平均速度和出砂总量的结果都已归纳完毕，现在利用方差分析法得到上述两因变量的分析结果，见表7、表8。各因素水平对两因变量的影响情况如图10、图11所示。

首先，收缩角、喉部半径以及扩散角的值分别设为F、F和F。根据显著性判断准则，从表7可知，F=3716.044>0.001(2,2)=999.00，喉部半径的水平变化对出砂平均速度有极显著的影响；0.001(2,2)=999.00>F=380.102>0.01(2,2)=99.00，收缩角的水平变化对出砂平均速度有显著性影响；F=2.544<0.01(2,2)=99，扩散角的水平变化对出砂平均速度影响极小。由图10可知，随着喉部半径的增加，出砂平均速度呈线性增大。当喉部半径从3 mm增加至5 mm时，出砂平均速度从85.36 m/s增大至128.59 m/s，增加了50.6%。随着收缩角的增加，出砂平均速度反而逐渐减少。当收缩角从30°增大至50°时，出砂平均速度从114.70 m/s降低至100.86 m/s，降低了12%。随着扩散角水平的增大，出砂平均速度变化基本不大。

表7 出砂平均速度

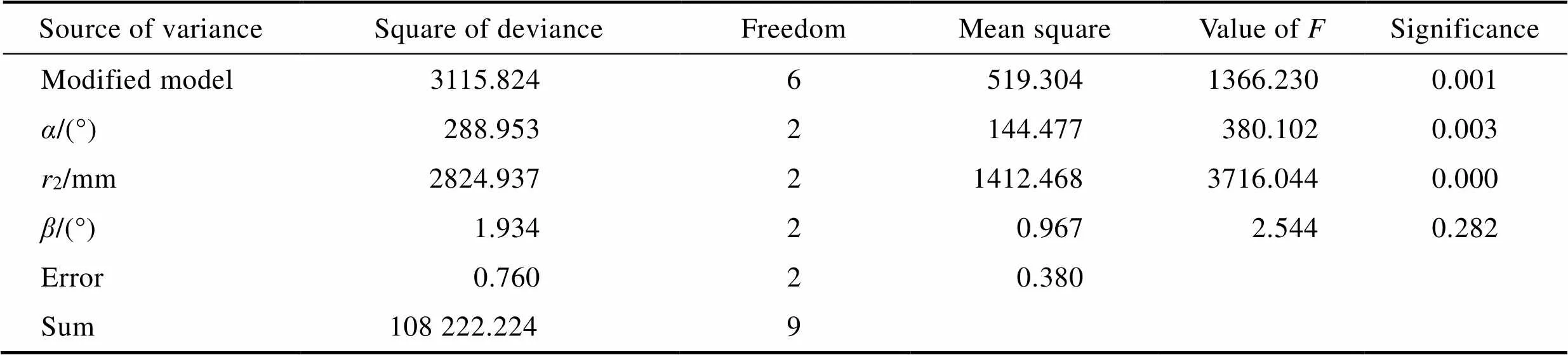
Tab.7 Average sand production speed

表8 出砂总量

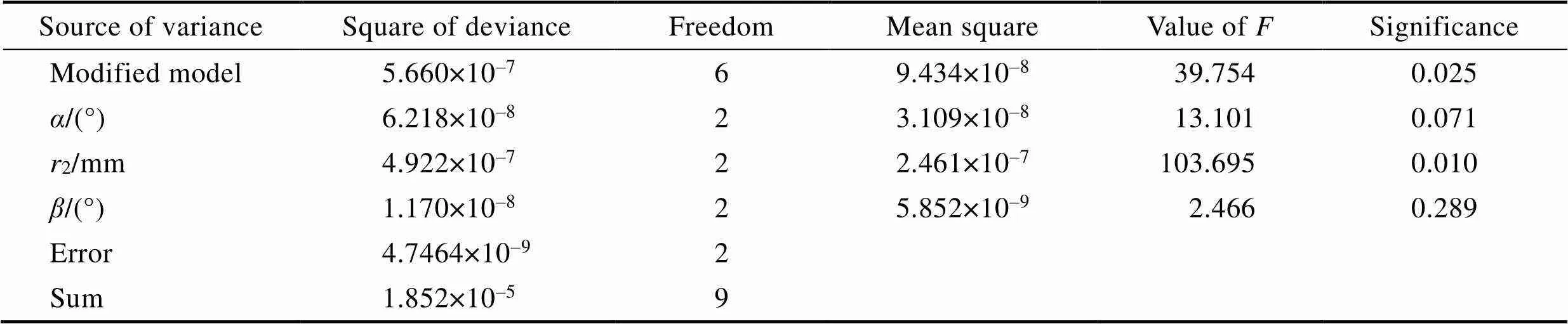
Tab.8 Total of sand production

图10 各因素水平对出砂平均速度的影响

图11 各因素水平对出砂总量的影响

从表8可知，F=103.695>0.01(2,2)=99.00，喉部半径的水平变化对出砂总量有极显著的影响；0.05(2,2)= 19.00>F=13.101>0.1(2,2)=9，收缩角的水平变化对出砂总量有一定影响；F=2.466<0.1(2,2)=9，扩散角的水平变化对出砂总量影响最小。由图11可知，随着喉部半径的增大，出砂总量几乎呈线性减少。当喉部半径从3 mm增加到5 mm时，出砂总量从1.722× 10–3kg降低至1.158×10–3kg。收缩角从30°增大到50°时，出砂总量从1.320×10–3kg缓慢上升至1.522× 10–3kg。扩散角从3°增大到4°时，出砂总量的变化趋势基本不大。

方差分析中，喉部半径对出砂平均速度和出砂总量的影响最为显著。因此进一步探究分析其影响的规律和原因。运用控制变量法，现将收缩角和扩散角分别定为30°和3°，然后设置不同喉部半径进行7组仿真实验，其值分别为3、4、5、6、7、8、9 mm，得到了喉部半径和出砂平均速度的关系，如图12所示。可以看出，随着喉部半径不断增大，出砂平均速度也增大，在喉部半径为6～9 mm时趋于平缓，且到达了一个峰值。当喉部半径为8 mm时，出砂平均速度为184.65 m/s，喉部半径增大到9 mm时，有了些许下降。分析Fluent中的压力云图（图13）可知，喉部半径越大，喉部区域压强越小，喷嘴内形成的压力差越大，导致气相流速增大，进而使出砂平均速度增大。

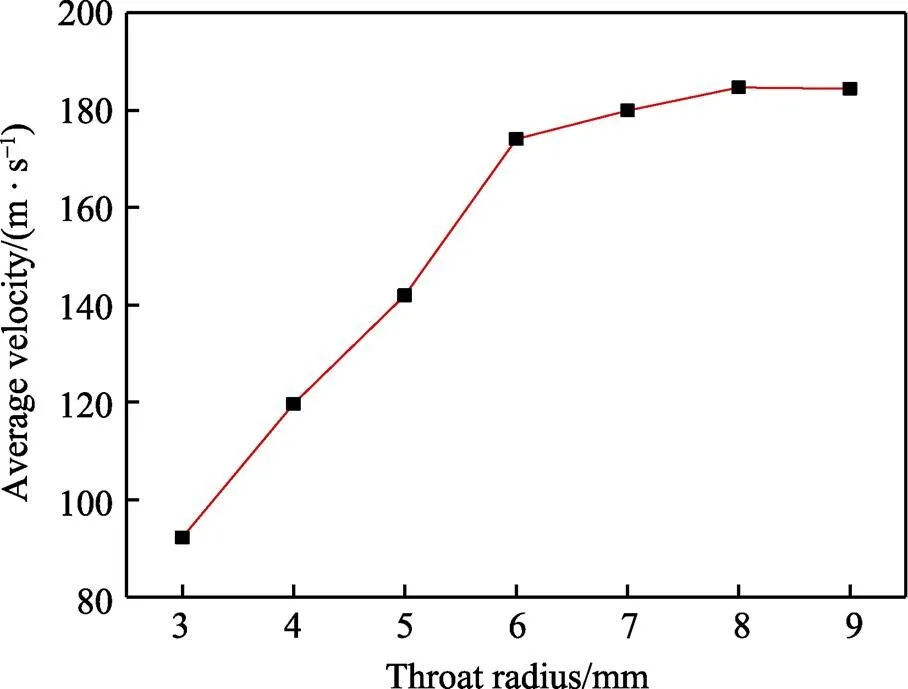
图12 喉部半径对出砂平均速度的影响

在仿真过程中0.3 s时，喉部半径和收缩段砂粒质量关系变化曲线如图14所示。由图14可知，随着喉部半径的增大，收缩段砂粒质量逐渐减小，并在7～9 mm时趋于平缓。为了能够直观地察看收缩段砂粒的具体状态，取喉部半径为3、6、9 mm收缩段部分的切片，如图14中插图所示，可以看出统计网格内砂粒的分布状态和这一瞬时的砂粒质量。造成这一现象的原因是在砂粒生成速率相同的情况下，喉部半径越大，砂粒速度越大，砂粒在喷嘴内停留的时间越短（如图15所示），导致收缩段待喷出的砂粒越稀疏。因此，在单位时间内，随喉部半径的增大，从喷嘴出口处统计的出砂总量减少。

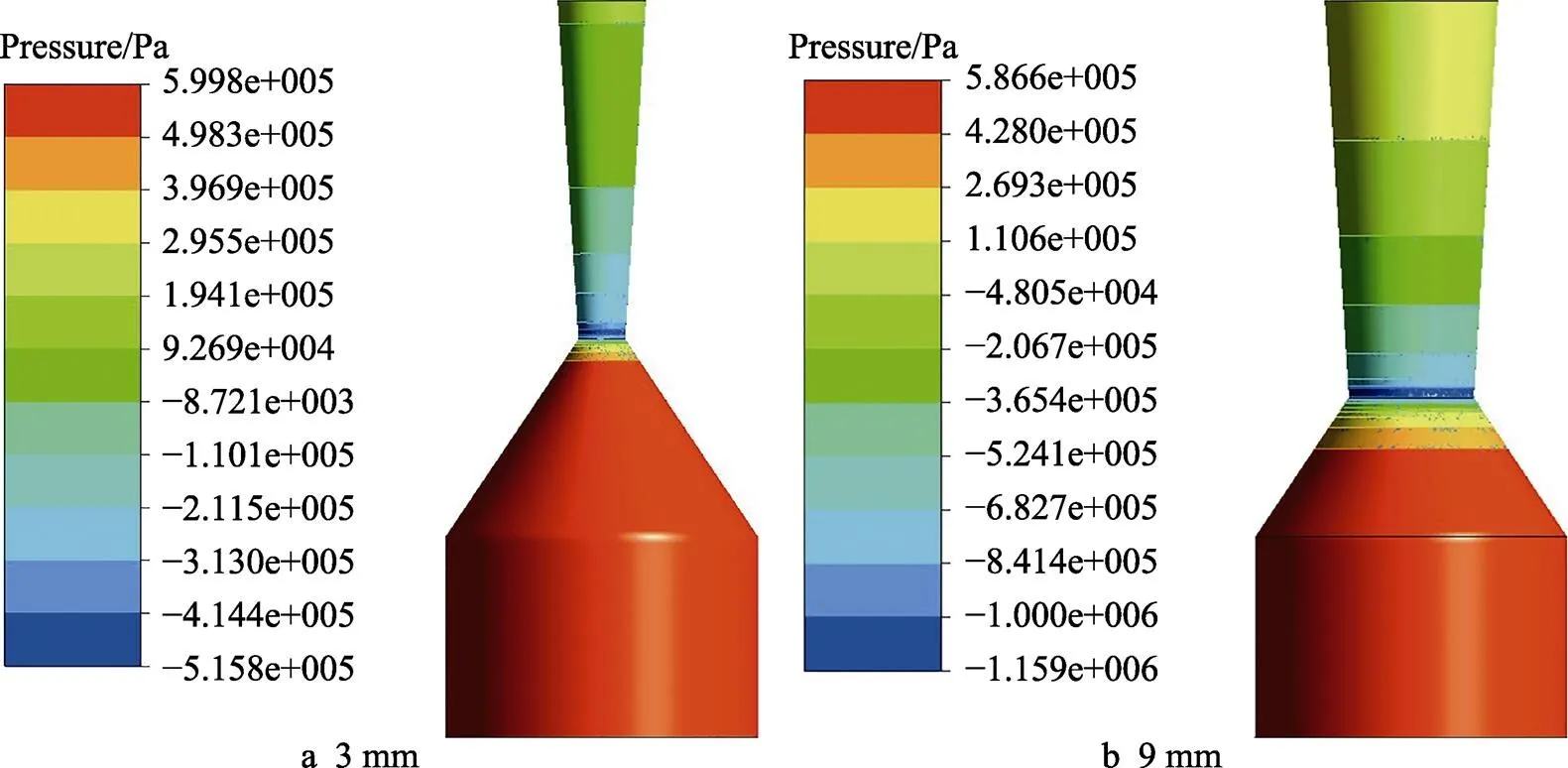
图13 不同喉部半径的压力云图

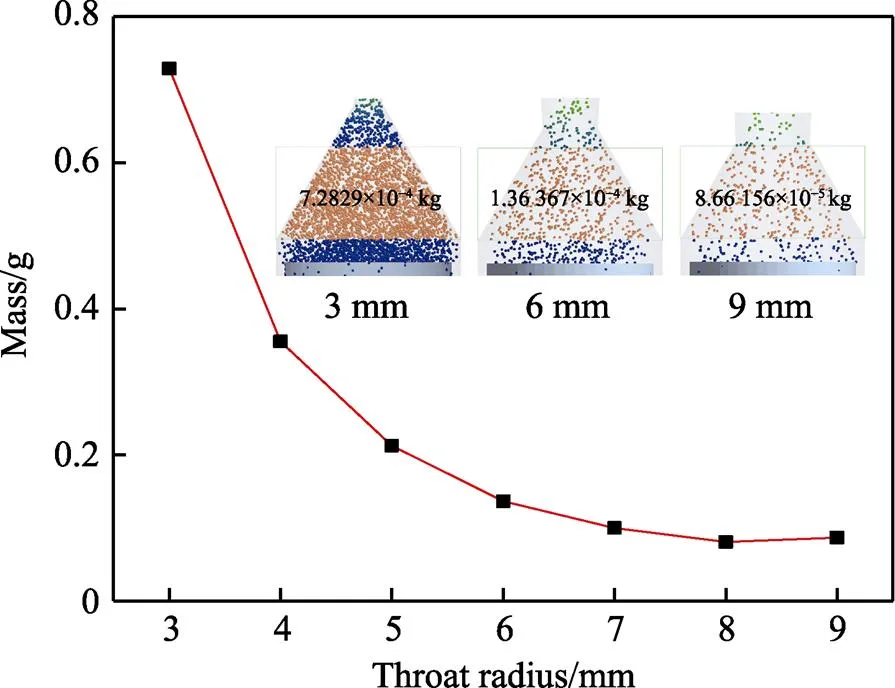
图14 在0.3 s时喉部半径对收缩段砂粒质量的影响

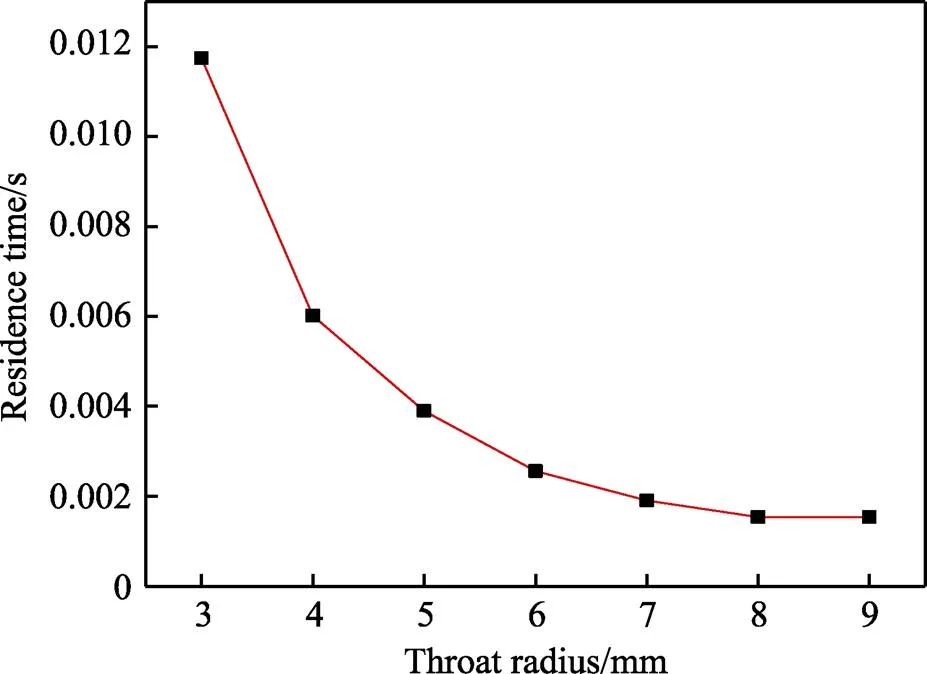
图15 喉部半径对砂粒在喷嘴内停留时间的影响

5 结论

通过离散元与有限元软件耦合模拟三维喷嘴模型中气固两相流场，然后对喷嘴不同的结构尺寸建立正交表进行仿真实验，研究收缩角、喉部半径以及扩散角的不同水平对出砂平均速度和出砂总量的影响规律，得出如下结论：

1）通过现有的EDEM-Fluent耦合办法对喷砂喷嘴进行气固两相流场模拟，应用了气相湍流以及颗粒运动的数学模型，分析讨论了喷砂过程中喷嘴气固两相的运动状态符合喷砂的基本原理，并验证了这一仿真模型的有效合理性。

2）喉部半径对出砂平均速度和出砂总量都有极显著的影响，收缩角对出砂平均速度有显著影响，对出砂总量有一定影响，扩散角对两者的影响基本不大。

3）由于喉部半径越大，喉部区域压强越小，喷嘴内形成的压力差越大，导致气相流速越大，进而使出砂平均速度增大。当然出砂平均速度也不是无限增大，从喉部半径为6 mm时，出砂平均速度开始缓慢增大，且在喉部半径为8 mm时，到达了峰值，其值为184.65 m/s。在砂粒生成速率相同的情况下，喉部半径越大，砂粒速度越大，砂粒在喷嘴内停留的时间越短，导致收缩段待喷出的砂粒越稀疏。因此，在单位时间内，随喉部半径的增大，从喷嘴出口处统计的出砂总量减少。

[1] GUO Qing, YANG Shu-zhen, YU Tao. A Novel Process Model of Ship Rust Removal by Premixed Abrasive Jet Based on Neural Network[J]. MATEC Web of Conferen­ces, 2019, 257: 02007.

[2] 李国英. 表面工程手册[M]. 北京: 机械工业出版社, 1998.

LI Guo-ying. Surface Engineering Manual[M]. Beijing: China Machine Press, 1998.

[3] 冯益华. 新型陶瓷喷砂嘴的研究开发及其冲蚀磨损机理研究[D]. 济南: 山东大学, 2003.

FENG Yi-hua. Development of New Ceramic Nozzles and Study on Its Erosion Wear Mechanisms[D]. Jinan: Shandong University, 2003.

[4] 李异. 金属表面清洗技术[M]. 北京: 化学工业出版社, 2007.

LI Yi. Metal Surface Cleaning Technology[M]. Beijing: Chemical Industry Press, 2007.

[5] 郝建军, 李会平, 马跃进, 等. 喷砂预处理在铸铁零件修复中的应用研究[J]. 农业机械学报, 2003, 34(4): 120-122, 126.

HAO Jian-jun, LI Hui-ping, MA Yue-jin, et al. Experi­mental Investigation on Repairing Iron Cast Parts with Grit-Blasting Pretreatment[J]. Transactions of the Chinese Society of Agricultural Machinery, 2003, 34(4): 120-122, 126.

[6] 孟立新, 张晞, 杨景顺. 热喷涂表面预处理工艺的优化[J]. 表面技术, 2005, 34(4): 55-57.

MENG Li-xin, ZHANG Xi, YANG Jing-shun. Optimi­zation of Surface Pretreating before Hot Spraying[J]. Sur­face Technology, 2005, 34(4): 55-57.

[7] MANDOLFINO C, LERTORA E, GAMBARO C. Effect of Surface Pretreatment on the Performance of Adhesive- Bonded Joints[J]. Key Engineering Materials, 2013, 554- 557: 996-1006.

[8] 王春水, 何声馨, 张二亮, 等. 喷砂表面的多尺度分析与表征[J]. 表面技术, 2015, 44(6): 127-132.

WANG Chun-shui, HE Sheng-xin, ZHANG Er-liang, et al. Analysis and Characterization of Sandblasted Surfaces Using Multi-Scale Analysis[J]. Surface Technology, 2015, 44(6): 127-132.

[9] 黄鑫. 喷砂处理对铝合金薄壁框架件形变的影响[D]. 长沙: 中南林业科技大学, 2018.

HUANG Xin. Effect of Shot Peening on Deformation of Aluminum Alloy Thin Wall Frame Parts[D]. Changsha: Central South University of Forestry & Technology, 2018.

[10] 李钦奉. 磨料用量与喷嘴直径相关关系的实验研究[J]. 表面技术, 2001, 30(4): 49-50.

LI Qin-feng. Experimental Research on Relationship between Grinding Quantity and Spray Nozzle Diame­ter[J]. Surface Technology, 2001, 30(4): 49-50.

[11] LIU Yong, ZHANG Juan, ZHANG Tao, et al. Optimal Nozzle Structure for an Abrasive Gas Jet for Rock Brea­kage[J]. Geofluids, 2018, 2018: 9457178.

[12] 曹玮. 基于CFD的气动喷砂机理与喷砂流场特性研究[D]. 大庆: 大庆石油学院, 2006.

CAO Wei. Study on Mechanism and Flow Field Charac­teristics of Pneumatic Sand Blasting Based on CFD[D]. Daqing: Daqing Petroleum Institute, 2006.

[13] 殷硕, 王晓放, 李文亚. 喷嘴出口直径对冷喷涂射流流场及基板最佳位置影响的数值分析[J]. 中国表面工程, 2013, 26(1): 74-78.

YIN Shuo, WANG Xiao-fang, LI Wen-ya. Numerical In­vestigations on the Effect of Nozzle Outlet Diameter on Jet Flow Field and Optimal Standoff Distance in Cold Spraying[J]. China Surface Engineering, 2013, 26(1): 74-78.

[14] JU H, ZHANG Z J, LIN C X, et al. Design Optimization and Experimental Study of Coaxial Powder-Feeding Nozzle in the Laser Cladding Process[J]. IOP Conference Series: Materials Science and Engineering, 2019, 474: 012008.

[15] 江竹亭, 甘振华, 吴南星, 等. 基于CFD的多孔陶瓷快速成型喷嘴结构设计优化[J]. 中国陶瓷, 2019, 55(7): 16-22.

JIANG Zhu-ting, GAN Zhen-hua, WU Nan-xing, et al. Structural Design and Optimization of Nozzle in Rapid Prototyping for Porous Ceramics Based on CFD[J]. China Ceramics, 2019, 55(7): 16-22.

[16] PENG Y Y, WANG J F, XIE J, et al. Structure Optimi­zation of Nozzle in Quick-Freezer Based on Response Surface Methodology[J]. IOP Conference Series: Earth and Environmental Science, 2018, 188: 012106.

[17] 刘雪梅, 顾佳巍, 祁国栋, 等. 基于CFD-DEM仿真的喷丸工艺参数优选[J]. 表面技术, 2018, 47(1): 8-15.

LIU Xue-mei, GU Jia-wei, QI Guo-dong, et al. Optimiza­tion of Shot Peening Process Parameters Based on CFD- DEM Simulation[J]. Surface Technology, 2018, 47(1): 8-15.

[18] MEZHERICHER M, BROSH T, LEVY A. Modeling of Particle Pneumatic Conveying Using DEM and DPM Methods[J]. Particulate Science and Technology, 2011, 29(2): 197-208.

[19] 杜俊, 胡国明, 方自强, 等. 弯管稀相气力输送CFD- DEM法数值模拟[J]. 国防科技大学学报, 2014, 36(4): 134-139.

DU Jun, HU Guo-ming, FANG Zi-qiang, et al. Simulation of Dilute Pneumatic Conveying with Bends by CFD- DEM[J]. Journal of National University of Defense Tech­no­logy, 2014, 36(4): 134-139.

[20] 马华庆, 赵永志. 喷动流化床中杆状颗粒混合特性的CFD-DEM模拟[J]. 浙江大学学报(工学版), 2020, 54(7): 1347-1354.

MA Hua-qing, ZHAO Yong-zhi. CFD-DEM Investigation on Mixing of Rod-Like Particles in Spout-Fluid Bed[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(7): 1347-1354.

[21] 郭柄江, 马学东, 赵磊, 等. 基于DEM-CFD耦合的谷物多级风选模拟研究[J]. 中国农机化学报, 2019, 40(10): 96-102.

GUO Bing-jiang, MA Xue-dong, ZHAO Lei, et al. Simu­la­tion Research of Grain Multi-Stage Wind Selection Based on DEM-CFD Coupling[J]. Journal of Chinese Agricultural Mechanization, 2019, 40(10): 96-102.

[22] 周良. 喷丸(砂)、喷涂技术及装备[M]. 北京: 化学工业出版社, 2008.

ZHOU Liang. Shot (Sand) Blasting, Spraying Technology and Equipment[M]. Beijing: Chemical Industry Press, 2008.

[23] 刘瑞江, 张业旺, 闻崇炜, 等. 正交试验设计和分析方法研究[J]. 实验技术与管理, 2010, 27(9): 52-55. LIU Rui-jiang, ZHANG Ye-wang, WEN Chong-wei, et al. Study on the Design and Analysis Methods of Orthogonal Experiment[J]. Experimental Technology and Manage­ment, 2010, 27(9): 52-55.

[24] CHEN Ju-kai, WANG Yue-she, LI Xiu-feng, et al. Ero­sion Prediction of Liquid-Particle Two-Phase Flow in Pi­pe­line Elbows via CFD-DEM Coupling Method[J]. Pow­der Technology, 2015, 282: 25-31.

[25] CROWE C T. On Models for Turbulence Modulation in Fluid-Particle Flows[J]. International Journal of Multi­phase Flow, 2000, 26(5): 719-727.

[26] 袁竹林, 朱立平, 耿凡. 气固两相流动与数值模拟[M]. 南京: 东南大学出版社, 2013.

YUAN Zhu-lin, ZHU Li-ping, GENG Fan. Gas Solid Two Phase Flow and Numerical Simulation[M]. Nanjing: Sou­theast University Press, 2013.

[27] 惠志全, 黄思, 黄家兴, 等. 基于EDEM-Fluent耦合的喷砂机磨损计算[J]. 武汉大学学报(工学版), 2020, 53(9): 825-830.

HUI Zhi-quan, HUANG Si, HUANG Jia-xing, et al. Wear Calculation of Sandblasting Machine Based on EDEM- Fluent Coupling[J]. Engineering Journal of Wuhan Uni­ver­sity, 2020, 53(9): 825-830.

[28] 张晴波, 郭涛, 洪国军, 等. 喷砂冲蚀实验中颗粒轨迹的数值预测[J]. 爆炸与冲击, 2021, 41(2): 158-165.

ZHANG Qing-bo, GUO Tao, HONG Guo-jun, et al. Nu­me­rical Prediction of Particle Trajectories in an Erosion Experiment[J]. Explosion and Shock Waves, 2021, 41(2): 158-165.

[29] 邓勃. 分析测试数据的统计处理方法[M]. 北京: 清华大学出版社, 1995.

DENG Bo. Statistical Processing Method of Analysis and Test Data[M]. Beijing: Tsinghua University Press, 1995.

Study on EDEM-Fluent Coupling Simulation of Nozzle Structure Parameters in Sandblasting Process

1,1,1,1,1,2

(1.School of Mechanical Engineering and Automation, University of Science and Technology, Anshan 114051, China; 2.Anshan Changhe Metallurgical Equipment Manufacturing Co. Ltd., Anshan 114031, China)

This paper aims to study the influence rule and reason of the contraction angle, throat radius and diffusion angle of the nozzle on the average sand production speed and total sand production amount during the process of sandblasting. The EDEM-Fluent coupling model was used to simulate the gas-solid two-phase movement in the sandblasting nozzle, and the correctness of the model was verified by experiments. The simulation experiment was carried out by setting the orthogonal table with different structure sizes of nozzles. The analysis of variance method (test) was used to analyze the variation rule of average sand production speed and total sand production amount at each factor level. The influence reason of throat radius on average sand production speed and total sand production amount was further explored by using the control variable method.From the variance analysis of the average sand production speed, thevalue of throat radius to 3716.044 and thevalue of contraction angle to 380.102, the average sand production speed increased rapidly with the increase of throat radius, but decreased with the increase of contraction angle;From the variance analysis of the total sand production amount, thevalue of throat radius to 103.695 and thevalue of contraction angle to 13.101, the total sand production amount decreased rapidly with the increase of throat radius, but increased slowly with the increase of contraction angle;When the contraction angle and diffusion angle were invariable, the negative pressure increased with the increase of throat radius, resulting in the increase of gas phase flow speed, and then the average sand production speed increased. When the throat radius increased to 8 mm, the average sand production speed no longer increased and slightly decreased, and its peak value was 184.65 m/s;In the case of the same sand generation rate, it is concluded that the larger the throat radius, the greater the sand speed, the shorter the residence time of the sand in the nozzle, and the less the mass of sand to be ejected from the contraction section and the more sparse the distribution state. It was verified that EDEM-Fluent coupling simulation of gas-solid two-phase flow field in nozzle was feasible and reasonable.Based on this simulation model, the relationship between average sand production speed and total sand production amount and different nozzle structural parameters was obtained, among which the throat radius had the most significant effect on the two.The larger the throat radius, the greater the average sand production speed, the less the total amount of sand counted at the nozzle outlet per unit time.

structure of nozzle; EDEM-Fluent coupling; average sand production speed; total sand production amount; variance analysis;test

2021-03-15；

2021-06-23

ZHOU Da-peng (1995—), Male, Master, Research focus: particle matter dynamics.

马学东（1965—），男，博士，教授，主要研究方向为颗粒物质动力学。

Corresponding author：MA Xue-dong (1965—), Male, Doctor, Professor, Research focus: particle matter dynamics.

周大鹏, 马学东, 杜昱霖, 等. 喷砂工艺的EDEM-Fluent耦合模拟喷嘴结构参数的研究[J]. 表面技术, 2022, 51(1): 192-201.

TG668

A

1001-3660(2022)01-0192-10

10.16490/j.cnki.issn.1001-3660.2022.01.020

2021-03-15；

2021-06-23

国家自然科学基金项目（51775258）；辽宁省自然科学基金重点项目（20170540458）；精密与特种加工教育部重点实验室基金（B201703）

Fund：Supported by National Natural Science Foundation of China (51775258); Natural Science Foundation Plan Key Projects of Liaoning Province (20170540458); Key Laboratory Fund of Ministry of Education for Precision and Special Processing (B201703)

周大鹏（1995—），男，硕士，主要研究方向为颗粒物质动力学。

ZHOU Da-peng, MA Xue-dong, DU Yu-lin, et al. Study on EDEM-Fluent Coupling Simulation of Nozzle Structure Parameters in Sandblasting Process[J]. Surface Technology, 2022, 51(1): 192-201.