牵制控制含噪声的多延迟超网络的结构识别

赵雪漪,朱帅兵,邓乐斌,谢 红

(1.汉江师范学院数学与计算机科学学院,湖北 十堰 442000)

(2.湖南师范大学数学与统计学院计算与随机数学教育部重点实验室,湖南 长沙 410081)

1 引言

在过去的二十年中,大型互连系统通常被建模为单层复杂网络.复杂网络的研究涉及到不同的学科领域,受到了各学科研究人员的广泛关注[1-9].在现实世界中,复杂网络通常并不是单独存在,而是通过相互作用形成超网络.比如,在疾病传播网络中,传染病的大爆发会引发信息传播网络上消息爆发,而消息的传播会增大疾病的爆发阈值；社交网络中,人们之间的关系网络（家人、朋友、同事等）和通信网络（电话、微信、QQ等）是错综复杂相互作用的.以上这些网络就称为超网络,网络嵌套或包含着若干个子网络,子网络之间通过某种方式连接在一起.对超网络的研究是复杂网络领域最重要和最前沿的研究方向之一[10-15].目前关于超网络的动力学方面的研究还很少,近几年所研究的大多数超网络,都是不含延迟或者是含有单个延迟,这是很理想的状态.在现实世界中,一个网络中可能含有多种延迟.比如说通信网络,两个人之间通过微信或者QQ联络,那么不同的通信方式所产生的延迟就是不同的；在交通网络中,航空或者是高速等不同的运输方式所产生的延迟也是不同的.在超网络中,每一层的节点之间可以有多种耦合方式,不同的耦合方式产生不同的延迟,具有相同延迟的节点结合一起形成层内的子网络,这种每一层含有多种延迟的超网络称为多延迟超网络,如图1,不同的颜色代表不同的层,每一层有各自不同的延迟、噪声强度和耦合强度.

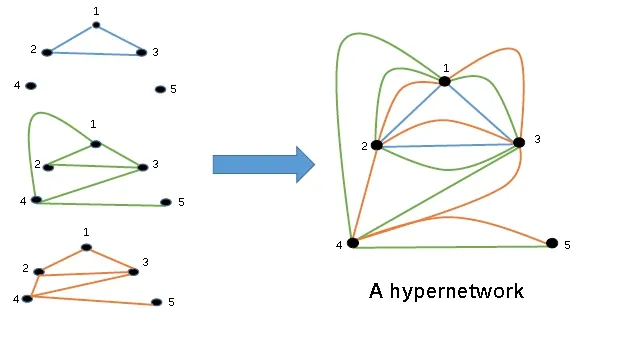
图 1 三层多延迟超网络模型,不同的颜色代表不同层,每一层有各自不同的延迟、噪声强度和耦合强度

在自然、社会和工程实际中,准确的拓扑结构往往是未知的或者是不确定的.因此,根据网络的节点动力学来反演网络的拓扑结构,这个问题越来越引起各个相关领域研究者们的重视.网络结构的识别具有重大的理论和应用价值,它也是分析控制和预测真实的复杂网络动力学行为的先决条件.对于网络的拓扑结构识别问题,最近几年获得一些重要进展,有很多种识别方法,比如基于自适应同步的网络拓扑识别方法[16-19],压缩感知方法利用实际复杂网络邻接矩阵的稀疏性以及目标优化思想反演网络结构[20,21],基于格兰杰因果检验的网络拓扑结构的识别方法则是根据实测时间序列数据推断节点间的有向关系[22],这些方法都取得了很好的效果,并且在进一步地发展.另外,在文章[23-25]中,分别给出了基于同步的识别方法中,保证成功进行拓扑结构识别的几个条件.对单层网络的拓扑识别问题的研究已经取得了丰硕的成果,但是目前对超网络拓扑识别的研究还很少,对超网络的拓扑识别问题是目前网络科学重要的分支之一.

在实际复杂网络中,我们通常只对一部分网络的拓扑结构感兴趣,比如说在社会网络,我们只想知道朋友或家人的信息；在生物神经网络,细胞神经元个数繁多,全部识别不切实际,可以根据实际情况识别部分网络.因此,通过牵制控制的方法,不需要接收原始网络中所有节点的信息,通过牵制控制一部分节点,来识别原网络其中一部分未知的拓扑结构是有实际意义的.近几年,对牵制控制的研究有很多好的成果[26-30],但是牵制控制超网络的研究还很少.在现实世界中,噪声是无处不在的,系统受到内部或外部的干扰,都会产生噪声.同时,噪声也是一把“双刃剑”,比如科学家制成一种激光听力诊断装置,它由光源、噪声发生器和电脑测试器三部分组成,可以通过噪声的原理来治病.但是长期的噪声污染又会引发疾病,因此,怎样利用好噪声是一个亟待解决的问题,对噪声系统的研究也引起了人们的广泛关注.

基于以上讨论,本文利用同步理论,通过牵制控制方法,不需要接收原网络中所有节点的信息,通过牵制控制一部分节点,来识别含噪声的多延迟超网络中的未知拓扑结构.数值仿真验证了定理的有效性,说明用牵制控制方法研究超网络的未知拓扑结构是有效的,具有实际意义.本文共有五个部分,第二部分介绍了文章的一些引理和预备知识,第三部分是本文的主要理论结果,第四部分用数值仿真验证定理的有效性,第五部分是结论.

2 预备知识

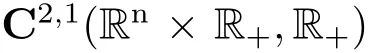
考虑如下n维随机微分方程

对于任意的初始向量x0,方程(2.1)的解定义为x(t;t0,x0).当f(t,0,0)=φ(t,0,0)=0,方程(2.1)有一个平凡解x(t0)≡ 0.这里,(Ω,F,{Ft}t≥0,P)表示完备概率空间,w(t)=(w1(t),...,wn(t))T是定义在概率空间上的n维布朗运动.

引理1[31]

引理2(Schur Complement[32])线性矩阵不等式

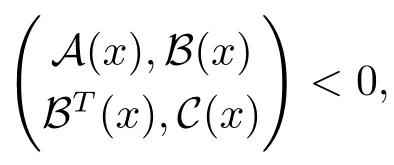
其中AT(x)=A(x),CT(x)=C(x),等价于以下任意一个条件

(a)A(x)＜0且C(x)-BT(x)A(x)-1B(x)＜0;

(b)C(x)＜0且A(x)-BT(x)C(x)-1B(x)＜0.

引理3[33]假设P是对角矩阵,第k个(k=1,2,···,l)对角元素是p,其余元素为0,其中p＞0是足够大的数.因此,G-P＜0等价于Gl＜0.

3 主要结论

本文主要考虑如下含噪声的多延迟超网络(3.1):

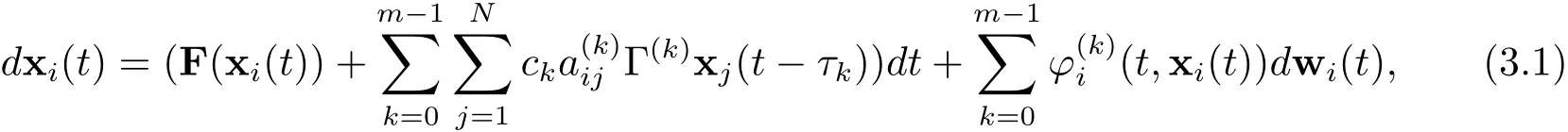
本节的目的就是通过设计自适应牵制控制器,来识别多层网络(3.1)的系统参数和部分未知拓扑结构.令多层网络(3.1)为驱动网络,并相应地设计响应网络如下：

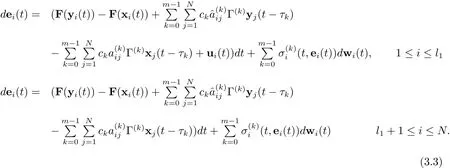
在得到主要结论之前,我们先给出几个假设：

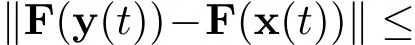
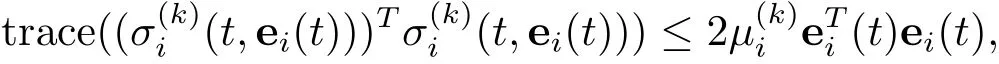
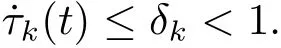
定理1如果假设1-4成立.若存在合适的正数l1使得

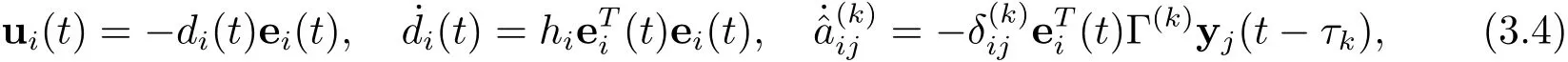
这里i=1,2,···,l1,j=1,2,...,l2,hi是正常数,含噪声的多延迟超网络(3.1)的未知拓扑结构可以被成功识别,同时,驱动网络和相应网络达到同步.

证考虑如下李雅普诺夫函数：

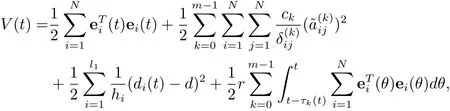
这里d＞0,r＞0是常数.我们得到

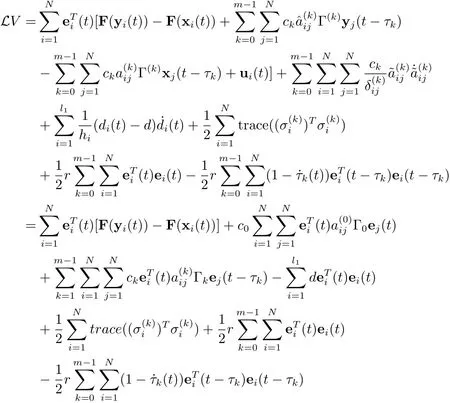
注由定理1可知,牵制控制的节点个数l与ck,μ,δ,γk有关,即与原网络的耦合强度、噪声强度、延迟和内连耦合矩阵有关.

4 数值仿真

由定理1可知,存在合适的正常数l1和r,只需要牵制控制l1个节点,就可以识别多延迟超网络的部分拓扑结构,并且使得驱动系统(3.1)和响应系统(3.2)达到完全同步.考虑含有10个Rossler系统的三层网络,

由图2可知Rossler系统是有界的[34],并且存在M1=10,M2=10,M3=35,使得||xij||≤ Mj,||yij||≤ Mj,i=1,2,···,10,j=1,2,3.

图 2:Rssler系统 (a=0.2,b=0.2,c=7).

因为

所以

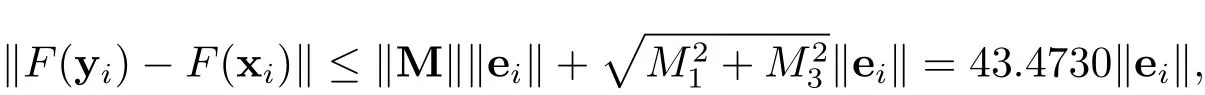
满足假设1,α=43.4730.

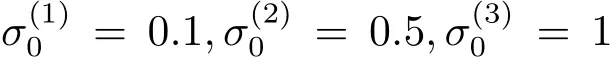
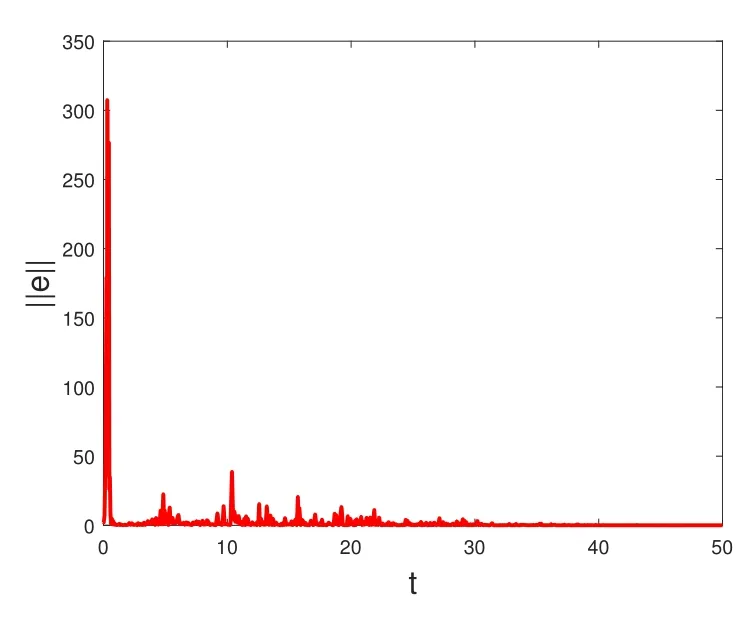
图3:牵制控制一个节点的同步误差图.

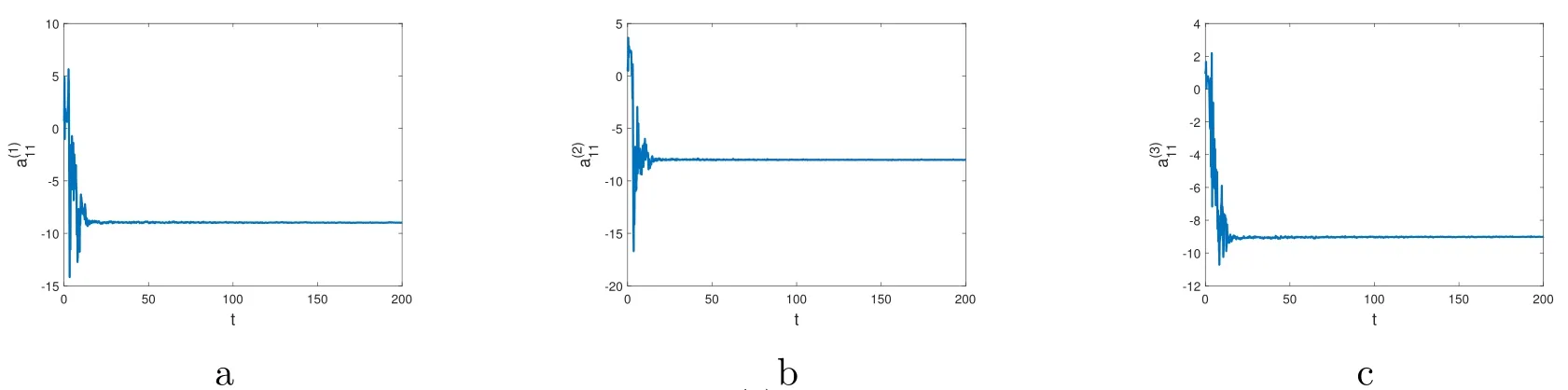
图4:拓扑结构a,k=1,2,3的估计图.

5 结论

本文构造了含噪声的多延迟超网络,基于同步的拓扑识别方法和随机微分方程的理论基础,通过设计合适的牵制控制器,牵制控制一部分节点,将原始网络当作驱动网络,构造响应网络来识别原网络的未知拓扑结构.数值仿真验证了定理的有效性,接下来我们会进一步研究各种网络参数对拓扑识别的影响.