ON SPLIT REGULAR BIHOM-LIE COLOR ALGEBRAS
CAO Yan,TAO Ya-ling
(1.School of science,Harbin University of Science and Technology,Harbin 150080,China)
(2.Heilongjiang Provincial Key Laboratory of Optimization Control and intelligent Analysis for Complex Systems,Harbin University of Science and Technology,Harbin 150080,China)
Abstract:The aim of this article is to study the structure of split regular BiHom-Lie color algebras.By developing techniques of connections of roots for this kind of algebras,we show that such a split regular BiHom-Lie color algebra L is of the formwith U a subspace of the abelian(graded)subalgebra H and any I[α],a well described(graded)ideal of L,satisfying[I[α],I[β]]=0 if[α]/=[β].Under certain conditions,in the case of L being of maximal length,the simplicity of the algebra is characterized and it is shown that L is the direct sum of the family of its simple(graded)ideals.
Keywords: BiHom-Lie color algebra;split;root space;root system
1 Introduction
The origin of Hom-structures can be found in the physics literature around 1990,appearing in the study of q-deformations of algebras of vector fields,especially Witt and Virasoro algebras,see for instance[1–3].So far,many authors have studied Hom-type algebras[4–11].A BiHom-algebra is an algebra in such a way that the identities defining the structure are twisted by two homomorphisms φ,ψ.The notion of BiHom-Lie algebras was introduced in[12],which is intimately related to both Lie algebras and Hom-Lie algebras.The case of φ= ψ=Id implies BiHom-Lie algebras are Lie algebras and the other case of φ= ψ give Hom-Lie algebras.The notion of Lie color algebras was introduced as generalized Lie algebras in 1960 by Ree[13].In particular,BiHom-Lie color algebras are defined as an extension of BiHom-Lie(super)algebras to Γ-graded algebras,where Γ is any abelian group.
As is well-known,the class of the split algebras is specially related to addition quantum numbers,graded contractions and deformations.Recently,the structure of different classes of split algebras have been studied by using techniques of connections of roots(see for instance[14–23]).In the present paper we introduce the class of split BiHom-Lie color algebras of arbitrary dimension as the natural extension of the class of split BiHom-Lie superalgebras studied in[24]and the class of split Lie color algebras studied in[19].The purpose of this paper is to consider the structure of split regular BiHom-Lie color algebras by the techniques of connections of roots based on some work in[14,16,17,22,24].
Throughout this paper,split regular BiHom-Lie color algebras L are considered of arbitrary dimension and over an arbitrary base field.This paper is organized as follows.In section 2,we establish the preliminaries on split regular BiHom-Lie color algebras theory.In section 3,we show that such an arbitrary split regular BiHom-Lie color algebra L with a symmetric root system is of the form L=U+P[α]∈Λ/~I[α]with U a subspace of the abelian(graded)subalgebra H and any I[α]a well described(graded)ideal of L,satisfying[I[α],I[β]]=0 if[α]/=[β].In section 4,we show that under certain conditions,in the case of L being of maximal length,the simplicity of the algebra is characterized and it is shown that L is the direct sum of the family of its simple(graded)ideals.
2 Preliminaries
First we recall the definitions of Lie color algebras and Hom-Lie color algebras.The following definition is well-known from the theory of graded algebra.
Definition 2.1[10]Let Γ be an abelian group.A bi-character on Γ is a map ε:Γ×Γ →{0}satisfying
(1) ε(α,β)ε(β,α)=1,
(2) ε(α,β + γ)= ε(α,β)ε(α,γ),
(3) ε(α + β,γ)= ε(α,γ)ε(β,γ),for all α,β,γ ∈ Γ.
It is clear that ε(α,0)= ε(0,α)=1 for any α ∈ Γ,where 0 denotes the identity element of Γ.
Definition 2.2[16]Let L= ⊕g∈ΓLgbe a Γ-graded K-vector space.For a nonzero homogeneous element v∈L,denote by, the unique group element in Γ such that v∈L,which will be called the homogeneous degree of v.We shall say that L is a Lie color algebra if it is endowed with a-bilinear map[·,·]:L × L → L satisfying
Lie superalgebras are examples of Lie color algebras with Γ =and ε(i,j)=(-1)ij,for any i,j∈.We also note that L0is a Lie algebra.
Definition 2.3[10]A Hom-Lie color algebra is a quadruple(L,[·,·],φ,ε)consisting of a Γ-graded-vector space L,an even bilinear mapping[·,·]:L × L → L,a homomorphism φ and a bi-character ε on Γ satisfying
Clearly Hom-Lie algebras and Lie color algebras are examples of Hom-Lie color algebras.Then we recall the definition of BiHom-Lie algebras and give the definition of BiHom-Lie color algebras.
Definition 2.4[12]A BiHom-Lie algebra over a field K is a 4-tuple(L,[·,·],φ,ψ),where L is a-linear space,[·,·]:L×L → L is a bilinear map and φ,ψ :L → L are linear mappings satisfying the following conditions:
(1)φ°ψ =ψ°φ,
(2)[ψ(x),φ(y)]=-[ψ(y),φ(x)],(BiHom-skew-symmetry)
(3)[ψ2(x),[ψ(y),φ(z)]]+[ψ2(y),[ψ(z),φ(x)]]+[ψ2(z),[ψ(x),φ(y)]]=0,(BiHom-Jacobi identity)
for any x,y,z∈L.
Definition 2.5A BiHom-Lie color algebra L is a quintuple(L,[·,·],φ,ψ,ε)consisting of a Γ-graded space L,an even bilinear mapping[·,·]:L × L → L,two homomorphisms φ,ψ and a bi-character ε on Γ satisfying
(1)φ°ψ =ψ°φ,
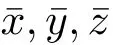
Lie color algebra are examples of BiHom-Lie color algebras by taking φ = ψ =Id.Hom-Lie color algebras are also examples of BiHom-Lie color algebras by considering ψ = φ.
Example 2.6Let(L,[·,·])be a Lie color algebra,φ,ψ :L → L two automorphisms and φ°ψ = ψ°φ.If we endow the underlying linear space L with a new product[·,·]′:L×L → L defined by[x,y]′:=[φ(x),ψ(y)]for any x,y ∈ L,then we have that(L,[·,·]′,φ,ψ)becomes a regular BiHom-Lie color algebra.
Throughout this paper we will consider a regular BiHom-Lie color algebra L being of arbitrary dimension and over an arbitrary base field.denotes the set of all nonnegative integers anddenotes the set of all integers.The usual regularity concepts will be understood in the graded sense.For instance,a subalgebra A of L is a graded subspace A= ⊕g∈ΓAgsuch that[A,A]⊂ A and φ(A)= ψ(A)=A.A graded subspace I= ⊕g∈ΓIgof L is called an ideal if[I,L]+[L,I]⊂ I and φ(I)= ψ(I)=I.A BiHom-Lie color algebra L will be called simple if[L,L]/=0 and its only(graded)ideals are{0}and L.
We introduce the concept of split regular BiHom-Lie color algebra in an analogous way.We begin by considering a maximal abelian graded subalgebra H= ⊕g∈ΓHgamong the abelian graded subalgebras of L.We observe that H is necessarily a maximal abelian subalgebra of L as the following lemma shows.
Lemma 2.7Let H= ⊕g∈ΓHgbe a maximal abelian graded subalgebra of a BiHom-Lie color algebra L.Then H is a maximal abelian subalgebra of L.
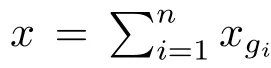
Let us introduce the class of split algebras in the framework of regular Lie color algebras L.First,we recall that a Lie color algebra(L,[·,·]),over a base field,is called split respect to a maximal abelian subalgebra H of L,if L can be written as the direct sum

where
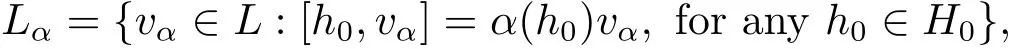
for a nonzero linear functional α on H0such that Lα/=0.
We introduce the concept of a split regular BiHom-Lie color algebra in an analogous way.
Definition 2.8We denote by H= ⊕g∈ΓHga maximal abelian(graded)subalgebra,of a regular BiHom-Lie color algebra L.For a linear functional α :H0→,we define the root space of L(with respect to H)associated to α as the subspace
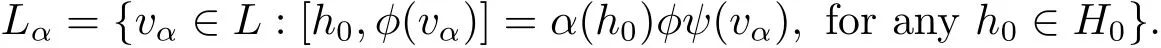
The elements α :H0→satisfying Lα/=0 are called roots of L with respect to H.We denote Λ :={α ∈ (H0)*{0}:Lα/=0}.We say that L is a split regular BiHom-Lie color algebra,with respect to H,if
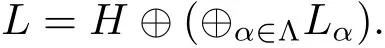
We also say that Λ is the root system of L.
Noting that when φ = ψ =Id,the split Lie color algebras become examples of split regular BiHom-Lie color algebras and when φ = ψ,the split regular Hom-Lie color algebras become examples of split regular BiHom-Lie color algebras.Hence,the present paper extends the results in[19,22].Let us see another example.
Example 2.9Let(L=H ⊕ (⊕α∈ΔLα),[·,·])be a split Lie color algebra,φ,ψ :L → L two automorphisms such that φ(H)= ψ(H)=H and φ°ψ = ψ °φ.By the Example 2.6,we know that(L,[·,·]′,φ,ψ),where[x,y]′:=[φ(x),ψ(y)]for any element x,y ∈ L,is a regular BiHom-Lie color algebra.Then it is straightforward to verify that the direct sum makes of the regular BiHom-Lie color algebra(L,[·,·]′,φ,ψ)a split regular BiHom-Lie color algebra,being the root system Λ ={αψ-1:α ∈ Δ}.
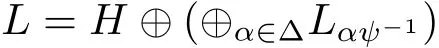
It is clear that the root space associated to the zero root L0satisfies H⊂L0.Conversely,given any v0∈L0we can write

where h ∈ H and vαi∈ Lαifor i=1,···,n,with αi/= αjif i/=j.Hence
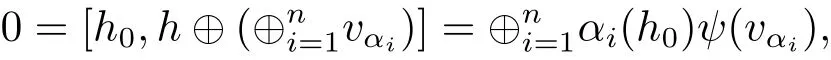
for any h0∈ H0.So taking into account the direct character of the sum and that αi/=0 gives us vαi=0 for i=1,···,n.So v0=h ∈ H.Consequently,

Lemma 2.10Let L= ⊕g∈ΓLgbe a split BiHom-Lie color algebra with corresponding root space decomposition L=H ⊕ (⊕α∈ΛLα).If we denote by Lα,g=Lα∩ Lg,then the following assertions hold.
(1)Lα= ⊕g∈ΓLα,gfor any α ∈ Λ ∪{0}.
(2)Hg=L0,g.In particular H0=L0,0.
(3)L0is a split BiHom-Lie algebra,respect to H0,with root space decomposition L0=H0⊕ (⊕α∈ΛLα,0).
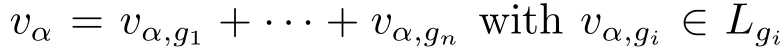
(2)Consequence of(2.1)and item 1.
(3)We also have Lg=Hg⊕ (⊕α∈ΛLα,g)for any g ∈ Γ.By considering g=0 we get L0=H0⊕ (⊕α∈ΛLα,0).Hence,the direct character of the sum and the fact that α /=0 for any α ∈ Λ gives us that H0is a maximal abelian subalgebra of the BiHom-Lie algebra L0.Hence L0is a split BiHom-Lie algebra respect to H0.
Lemma 2.11For any α∈Λ∪{0},the following assertions hold.
Proof(1)For any h0∈ H0and vα∈ Lα,since




To show φ-1(Lα)=Lαφ,the fact φ-1(Lα)⊂ Lαφis(2.4),while the fact Lαφ⊂ φ-1(Lα)is consequence of writing any element x ∈ Lαφof the form x= φ-1(φ(x))and applying(2.3).
(2)To verify

we observe that(2.2)gives us[ψ(h0),ψφ(vα)]= α(h0)ψφψ(vα),and so[ψ(h0),φψ(vα)]=αψ-1(ψ(h0))φψ(ψ(vα)).Since(2.2)and the identity ψ-1φ = φψ-1also gives us


ProofFor each h0∈ H0,vα∈ Lαand vβ∈ Lβ,we can write
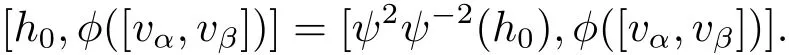
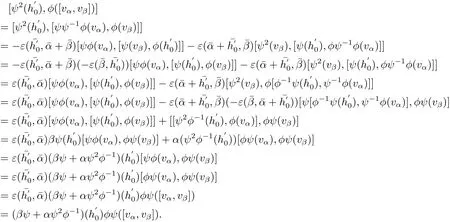
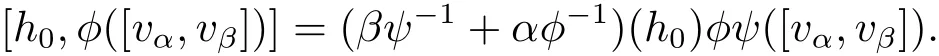
From Lemma 2.12 we can assert that
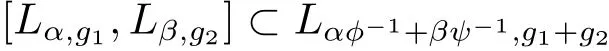
for any g1,g2∈ Γ.

ProofThis is a consequence of Lemma 2.11(1)and(2).
Definition 2.14A root system Λ of a split BiHom-Lie color algebra is called symmetric if it satisfies that α ∈ Λ implies-α ∈ Λ.
3 Decompositions
In the following,let L be a split regular BiHom-Lie color algebra with a symmetric root system Λ and L=H ⊕ (⊕α∈ΛLα)the corresponding root decomposition.We begin by developing the techniques of connections of roots in this section.
Definition 3.1Let α and β be two nonzero roots.We shall say that α is connected to β if there exists α1,···,αk∈ Λ such that
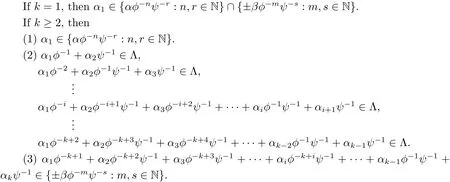
We shall also say that{α1,···,αk}is a connection from α to β.
Our next goal is to show that the connection is an equivalence relation on Λ.
Proposition 3.2The relation ~ in Λ,defined by α ~ β if and only if α is connected to β,is an equivalence relation.
ProofThis can be proved completely analogously to[14,Corollary 2.1].
For any α ∈ Λ,we denote by
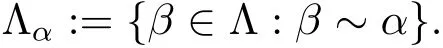
Clearly if β ∈ Λαthen-β ∈ Λαand,by Proposition,if γ /∈ Λαthen Λα∩ Λγ= Ø.
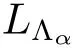

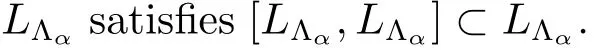



Similarly,we can also get



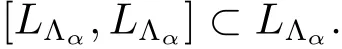

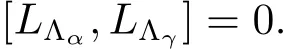
ProofWe have





Theorem 3.5The following assertions hold.
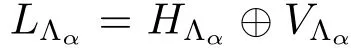

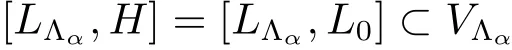
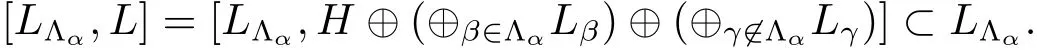
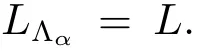

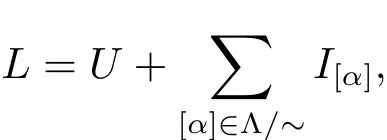

ProofBy Proposition 3.2,we can consider the quotient set Λ/ ~:={[α]:α ∈ Λ}.Let us denote by I[α]:=LΛα.We obtain that I[α]is well defined and by Theorem 3.5(1),an ideal of L.Therefore
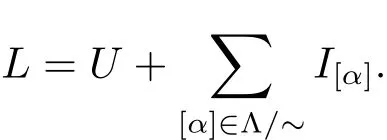
By applying Proposition 3.4 we also obtain[I[α],I[β]]=0 if[α]/=[β].
Let us denote by Z(L):={x∈L:[x,L]+[L,x]=0}the center of L.

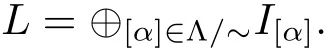
Furthermore[I[α],I[β]]=0,whenever[α]/=[β].
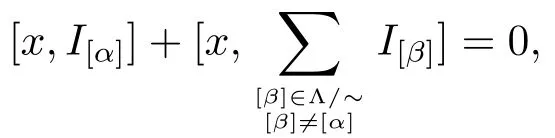
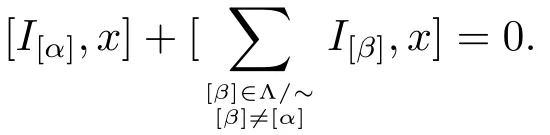
It implies[x,L]+[L,x]=0,that is,x∈Z(L)=0.Thus x=0,as desired.
4 The Simple Components
In this section,we study the sufficient conditions for the decomposition of L into direct sums of simple ideals.Under certain conditions we give an affirmative answer.
Lemma 4.1Let L=H ⊕ (⊕α∈ΛLα)be a split regular BiHom-Lie color algebra.If I is an ideal of L,then I=(I∩H)⊕(⊕α∈Λ(I∩Lα)).
ProofWe can see L=H ⊕ (⊕α∈ΛLα)as a weight module with respect to the split BiHom-Lie algebra L0,with maximal abelian subalgebra H0,in the natural way.The character of ideal of I gives us that I is a submodule of L.It is well-known that a submodule of a weight module is again a weight module.From here,I is a weight module with respect to L0(and H0)and so I=(I∩H)⊕(⊕α∈Λ(I∩Lα)).
Taking into account the above lemma,we observe that the grading of I and Lemma 2.10(1)let us write
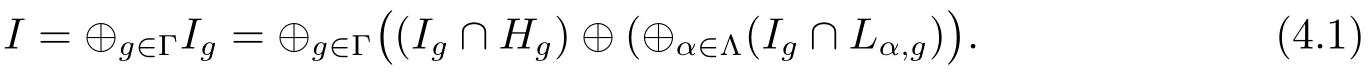
Lemma 4.2Let L be a split regular BiHom-Lie color algebra with Z(L)=0 and I an ideal of L.If I⊂H,then I={0}.
ProofWe suppose that there exists a nonzero ideal I of L such that I⊂H.We get[I,H]⊂ [H,H]=0 and[I,⊕α∈ΛLα]⊂ I ⊂ H.Then taking into account H=L0,we have[I,⊕α∈ΛLα]⊂ H ∩ (⊕α∈ΛLα)=0 and[⊕α∈ΛLα,I]⊂ (⊕α∈ΛLα)∩ H=0.From here I⊂Z(L)=0,which is a contradiction.
Let us introduce the concepts of root-multiplicativity and maximal length in the framework of split Hom-Lie color algebras.For each g ∈ Γ,we denote Λg:={α ∈ Λ :Lα,g/=0}.
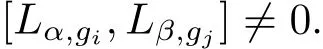
Definition 4.4A split regular BiHom-Lie color algebra L is of maximal length if for any α ∈ Λg,g ∈ Γ,we have dimLκα,κg=1 for κ ∈ {±1}.
If L is of maximal length,according to(4.1)we assert that given any nonzero ideal I of L then
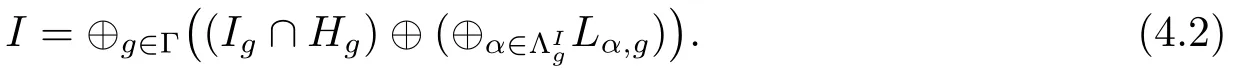

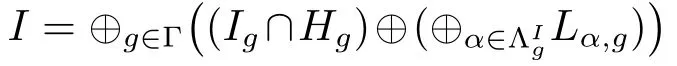


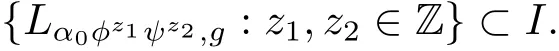
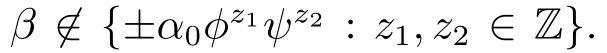
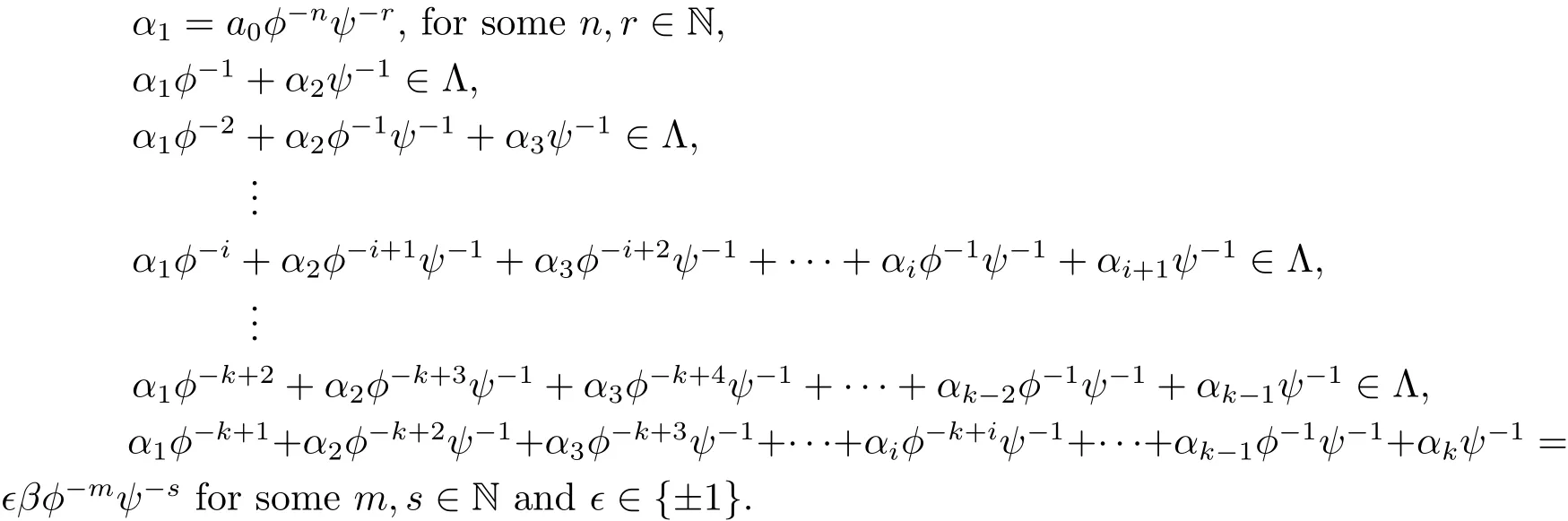




for some g2∈ Γ.Following this process with the connection{α1,···,αk},we obtain that


and for any β ∈ Λ.By Lemma 2.11,we can get
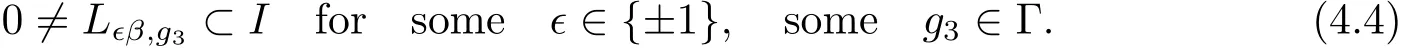
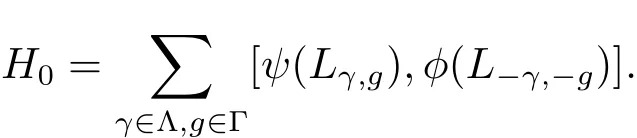
From here,there exists γ ∈ Λ and g4∈ Γ such that

By the BiHom-Jacobi identity either
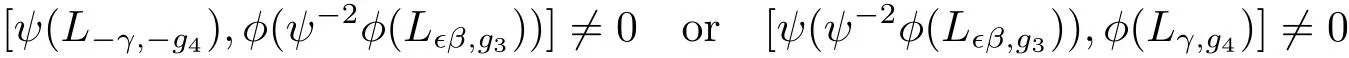
and so

That is

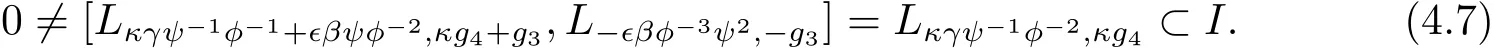
By Lemma 2.11(1),we can get

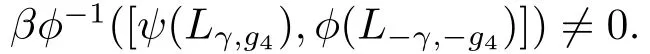
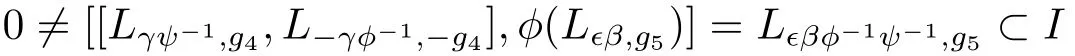
and so L∈β⊂ I.That is,we can assert that

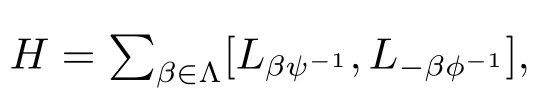

Now,given any-∈β ∈ Λ,by the facts-∈β/=0,H ⊂I and the maximal length of L we have

From(4.9)-(4.11)we conclude that I=L.Consequently L is simple.
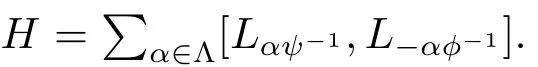
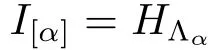
- 数学杂志的其它文章
- RESEARCH ANNOUNCEMENTS ON“MODERATE DEVIATIONS FOR GRENANDER ESTIMATOR NEARBOUNDARIES OF THE SUPPORT”
- ON REFINED YOUNG’S REVERSE INEQUALITIES FOR POSITIVE LINEAR OPERATORS
- SYMPLECTIC CRITICAL SURFACES WITH CIRCULAR ELLIPSE OF CURVATURE IN TWO-DIMENSIONAL COMPLEX SPACE FORMS
- STUDY ON 2-DIMENSIONAL SUBMANIFOLDS WITH CONSTANT DETERMINANT OF BLASCHKE TENSOR
- THE SPREADING SPEED FOR A NONLOCAL DIFFUSIVE PREDATOR-PREY MODEL WITH ONE PREDATOR AND TWO PREYS
- RESEARCH ANNOUNCEMENTS ON“UPPER BOUND ESTIMATES OF EIGENVALUES FOR HRMANDER OPERATORS ON NON-EQUIREGULAR SUB-RIEMANNIAN MANIFOLDS”

