RESEARCH ANNOUNCEMENTS ON“MODERATE DEVIATIONS FOR GRENANDER ESTIMATOR NEARBOUNDARIES OF THE SUPPORT”

GAO Fu-qing,JIANG Hui,ZHAO Xing-qiu

(1.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)

(2.School of Mathematics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

(3.Department of Applied Mathematics,Hong Kong Polytechnic University,Hong Kong 999077,China)

1 Introduction and Main Results

Let f be a decreasing density with support[0,∞).Denote by Fnthe empirical distribution function of a sample X1,...,Xnfrom f.Letbe the concave majorant of Fnon[0,∞),i.e.the smallest concave function such that

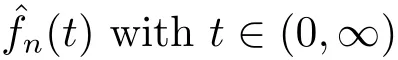
It should be noted that the Grenander estimatoris not consistent at boundaries([1],[10]).This phenomenon has great influences on the global measures of deviation,such as the Lk-distances with k＞1([2],[7])and L∞-distance([3]),because the inconsistency at the boundaries will dominate the convergence.

where c,α＞0,0＜α＜1.To be explicit,for the left boundary zero,suppose the following conditions hold:

(C1)0 ＜ f(0)=limt↓0f(t)＜ ∞;

(C2)there exists some positive constant ε0such that f has k-th order continuous derivative in(0,ε0]and f(ε0)/=0.Moreover 0 ＜ |f(k)(0)| ≤ supt≥0|f(k)(t)| ＜ ∞,with f(k)(0)=limt↓0f(k)(t)and f(i)(0)=0 for 1 ≤ i≤ k-1.

Moreover,in the case of 1/(2k+1)＜α＜1,

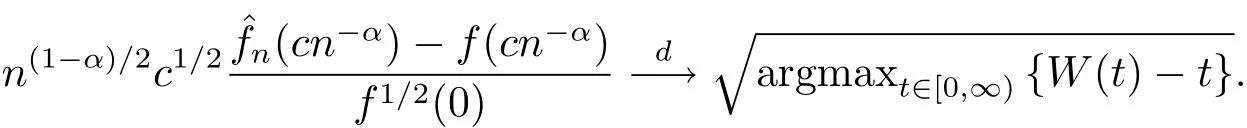
In this paper,the moderate deviations ofˆfn(cn-α)-f(cn-α)in the above two cases(0＜α＜1/(2k+1)and 1/(2k+1)＜α＜1)will be considered.By using strong approximation technique and comparison method,we obtain the following main results.

Theorem 1.1When 0＜α＜1/(2k+1),let‘nsatisfy as n→∞

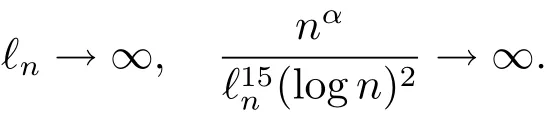
Then,under conditions(C1)and(C2),the sequence

satisfies the moderate deviations inwith speedand rate function,that is,for any open subset G of,

and for any closed subset F of,

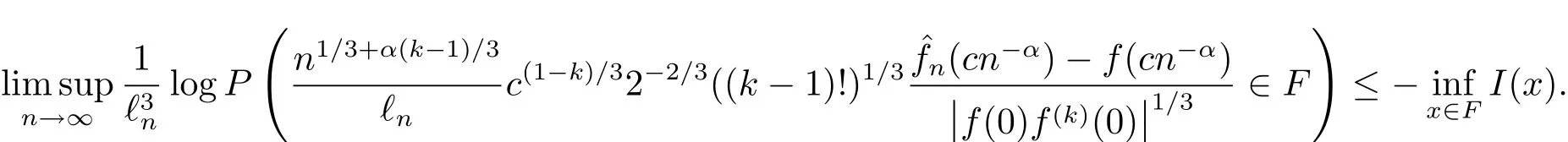
Remark 1For any x＞0,by Theorem 1.1,we have

Theorem 1.2When 1/(2k+1)＜ α ＜ 1,let{λn}satisfy that

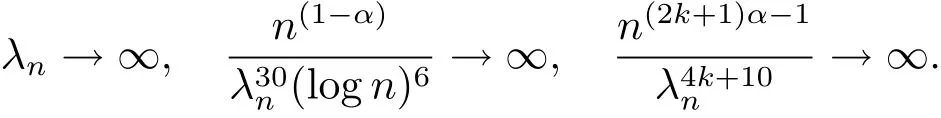
Then,under conditions(C1)and(C2),the sequence

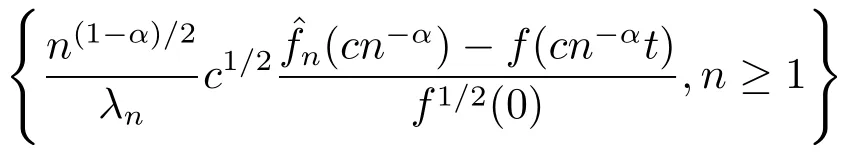
satisfies the moderate deviations inwith speedand rate function

Remark 2For any x＞0,by Theorem 1.2,we have

Remark 3If f has compact support,without loss of generality,assume it is the interval[0,1].The moderate deviations ofnear the right boundary 1(similar to Theorem 1.1 and Theorem 1.2)can also be obtained,and the details are omitted here.

For a detail study of the moderate deviations for Grenander estimator near boundaries,please refer to[5].