基于极限状态法的单轨轨道梁有限元分析
马 浩
(中铁宝桥集团有限公司,陕西 宝鸡 721006)
1 概述
跨座式旅游单轨近年来在国内发展迅速,其具有观光条件好、噪声小、节约城市空间、综合造价较低、环保等优点(见图1)。

其中轨道梁是系统主要受力构件,在设计过程中需进行强度、刚度等校核计算,设计标准以GB 8408—2018大型游乐设施安全规范[1]为主要依据(以下简称《规范》),以GB 50458—2008跨座式单轨交通设计规范为参考依据。
2018版《规范》提出了极限状态设计法,代表极限状态分析法在工程领域的进一步推广。闫岩[2]用极限状态法与容许应力法对铁路大跨连续梁设计对比分析。高策等[3-4]分析了容许应力法设计的不足,阐述了国内外极限状态法的推广和应用现状,指出现阶段极限状态法在铁路设计各专业中的应用情况。文献[5-6]地震工况下基于极限状态法分析了岸桥结构和铁路路基边坡等结构的抗震可靠性。文献[7-8]应用极限状态法分别对铁路钢桁梁桥、铁路路堑边坡等典型结构进行设计和计算,对极限状态法在铁路工程中的推广具有重要意义。岳凯等[9]采用极限状态法对起重机结构进行仿真计算,计算结果作为了轻量化设计的依据。文献[10-12]采用极限状态法对门式起重机、桥式起重机的典型结构进行分析,丰富和发展了极限状态法在起重机械领域的应用。张延昌等[13]以半潜式钻井平台为研究对象,研究承载力极限状态设计方法的应用。郭骁等[14]基于极限状态法分析双块式无砟轨道结构在多种荷载组合下的受力情况,并对道床板和底座板进行了配筋设计和裂缝检算。倪章军等[15]根据城市轨道交通桥梁的特点,并用实际算例说明极限状态法在设计中的可行性。随着极限状态法在工程领域的推广,也印证该设计方法相对容许应力法的优势,极限状态法综合考虑了载荷分布情况、材料性能、构件的工作条件,在铁路工程、城市轨道、起重机械、海底作业等复杂工况条件下,设计精确和可靠更为重要,利用Ansys Workbench建立轨道梁有限元模型,并依据《规范》中极限状态设计法,对轨道梁结构强度进行校核,采用对比论证极限状态设计法的可行性和优点,具有重要的工程价值。
2 极限状态法
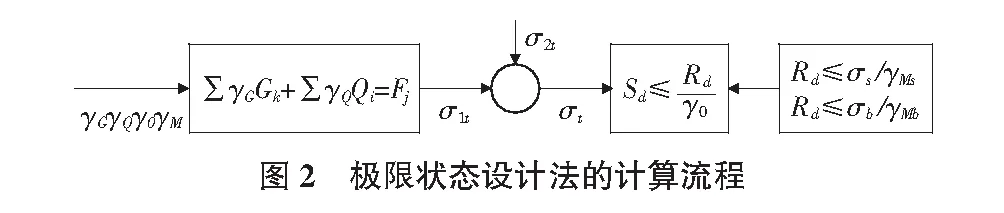
极限状态设计法是一种以概率理论为基础、以分项系数表达、不使结构超越某种规定极限状态的设计方法。现行的《规范》提出了极限状态设计法在承载能力验算中,载荷与载荷组合的原则。通过结构上的基本组合计算出应力σ1t,以及通过偶然载荷计算出应力σ2t,结合二者得出设计应力σt。将设计应力σt与载荷组合的效应Sd(应力)的最大值进行比较,载荷组合效应Sd的最大值由抗力设计值Rd和材料或构件的重要性系数γ0得到,而抗力设计值Rd可根据材料极限强度和抗力分项系数得出。极限状态设计法的计算流程如图2所示。
3 有限元分析
3.1 轨道梁结构
跨座式旅游单轨轨道梁作为系统的重要组成,是列车的导向和承重机构,是主要的受力构件。轨道梁为箱型结构,材料为Q345D,采用焊接连接,材料弹性模量E=2.10×105MPa,泊松比μ=0.3,屈服强度σs=345 MPa,抗拉强度σb=470 MPa。梁长24 m,支座板厚度40 mm,上盖板下盖板厚度20 mm,左右腹板厚度14 mm,隔板厚度8 mm,见图3。通过Ansys Workbench对轨道梁进行建模,主体结构采用Shell181单元,共43 173个单元,见图4。


3.2 荷载和约束条件
3.2.1 输入载荷
旅游单轨列车采用四编组,列车全长24 m,车宽2 m,车高3 m,重心高度距离轨面1 m。
1)永久载荷Gk包括梁自重Gk1和附加载荷Gk2=0.2Gk1。
2)活载荷Q1在不同工况下取值为:
满载活载荷Q1m:5轴,轴距5 250 mm,轴重40 kN。
偏载活载荷Q1p:5轴,轴距5 250 mm,轴重36 kN+2.0 kN·m。
空载活载荷Q1k:5轴,轴距5 250 mm,轴重32 kN。
3)紧急制动力Q2j=0.2Q1,Q1根据工况确定。
4)横向摇摆力大小为:单轴轴重的25%,单轴轴重根据工况确定。
5)风载荷Q4,分为正常运行风载荷Q4c和大风载荷Q4d。根据GB 50009建筑结构荷载规范的规定取值,正常运行基本风压:W0=0.14 kN/m2;大风载荷下风压W0=0.35 kN/m2。
6)雪载荷Q5,根据GB 50009建筑结构荷载规范的规定取值,雪载荷取0.2 kN/m2。
7)地震载荷Q6,根据GB 50011建筑抗震设计规范的规定取值,设计基本地震加速度值取0.15g。
8)温度载荷Q7,轨道结构制造安装时的基准温度为20 ℃,考虑整体升降温±30 ℃;轨道梁横向和竖向温差按15 ℃考虑。
3.2.2 载荷组合
轨道梁设计时考虑结构上可能同时出现载荷作用,取其最不利效应组合进行验算。极端条件工况是指在极限风速、地震等极限条件下的工况,列车处于停运状态。永久载荷组合工况是使用极限状态法时特有的一种组合工况。
1)满载急停制动工况,此工况下包含永久载荷Gk,满载活载荷Q1m、紧急制动力Q2j、风载荷Q4c、温度载荷Q7、横向摇摆力Q3。
Fj=1.1(Gk1+Gk2)+
1.35(Q1m+Q2j+Q4c+Q7+Q3)
(1)
2)偏载急停制动工况,此工况下包含永久载荷Gk,偏载活载荷Q1p、紧急制动力Q2j、风载荷Q4c、温度载荷Q7、横向摇摆力Q3。
Fj=1.1(Gk1+Gk2)+
1.35(Q1p+Q2j+Q4c+Q7+Q3)
(2)
其余载荷同满载急停制动工况。
3)极限状态工况,此工况下包含永久载荷Gk,空载活载荷Q1k、大风载荷Q4d、雪载荷Q5、地震载荷Q6、温度载荷Q7。
Fj=1.1(Gk1+Gk2)+
1.35(Q1k+Q4d+Q5+Q6+Q7)
(3)
4)永久载荷组合工况,根据《规范》所述,载荷设计值同时考虑下述组合。
Fj=1.35(Gk1+Gk2)
(4)
3.2.3 约束条件
X向为顺桥向,Y向为横桥向,Z向为竖直方向,轨道梁为简支梁结构,左端铰轴支座上,约束为UX,UY,UZ,ROX,ROZ,右端为滑动支座,约束为UY,UZ,ROX,ROZ。
3.3 极限状态下载荷效应值
根据《规范》附录E中规定,极限状态法分项系数取值范围,见表1。

表1 极限状态法分项系数取值表
基本组合一时,γG取1.35,基本组合二时,γG取1.1。对于重要的轴、销轴及Ⅰ级和Ⅱ级焊缝γ0≥1.5,对于一般构件γ0≥1.0。
根据极限状态法规定,Sd载荷组合的效应,广义指结构和构件的应力、应变、挠度、转角、内力、力矩或者其他极限状态控制值等,《规范》中限定为应力。求解载荷组合的效应Sd,需先求解抗力设计值Rd,设计抗力值采用两式中较小值:
Rd_max1=σs/γMs=287.5 MPa
(5)
Rd_max2=σb/γMb=213.6 MPa
(6)
其中式(5)中γMs取1.2,式(6)中γMb取2.2。
抗力设计值Rd_max=213.6 MPa,载荷组合的效应Sd等于:
Sd_max=Rd/γ0=178 MPa
(7)
式(7)中结构或构件的重要性系数γ0取1.2。
3.4 极限状态下有限元分析
在四种不同工况下,分别对轨道梁进行有限元分析,得到轨道梁在不同荷载组合作用下的最大应力值,并与应力极限值进行比较。四种工况的有限元分析结果见图5。
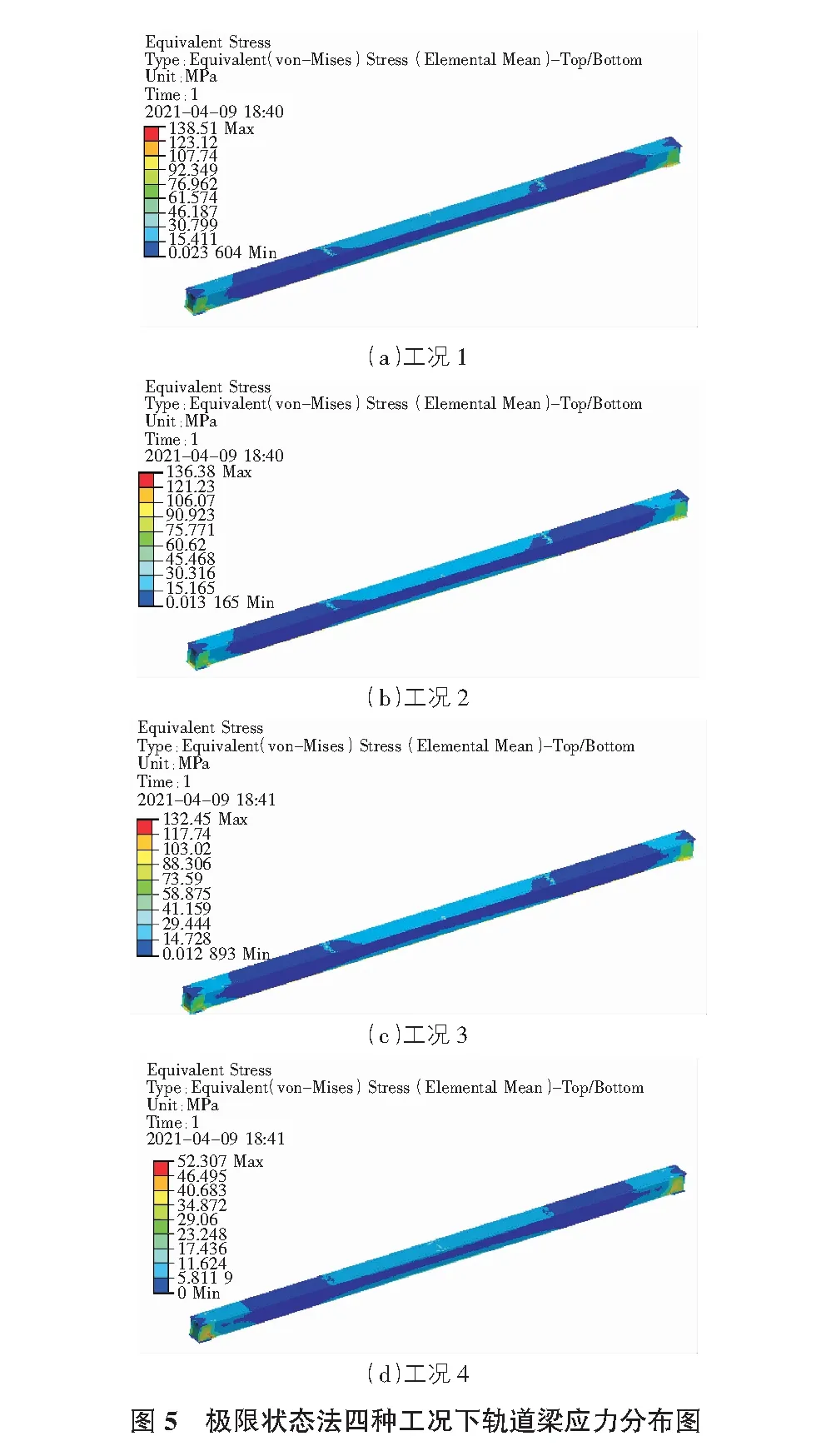
由图5(a)可知,满载急停制动工况应力为138.5 MPa,由图5(b)可知,偏载急停制动工况应力为136.4 MPa,由图5(c)可知,极限状态工况应力为132.5 MPa,由图5(d)可知,永久载荷组合工况应力为52.3 MPa,满载急停制动工况应力值最大,此工况为最不利工况,应力值138.5 MPa,小于应力极限值178 MPa,则应力安全余量为39.5 MPa。
4 极限状态法与容许应力法的对比分析
容许应力法的设计原理与极限状态设计法的原理基本一致。模型、载荷、约束条件同极限状态法。
4.1 容许应力法的工况、载荷组合
选择满载急停制动工况和偏载急停制动工况与极限状态法进行对比。根据《规范》,采用容许应力法时,冲击系数k1≥1.2,且当列车速度大于20 km/h时,轨道受到的载荷还应考虑不小于1.2的振动系数k2。
1)满载急停制动工况,此工况下包含永久载荷Gk,满载活载荷Q1m、紧急制动力Q2j、风载荷Q4c、温度载荷Q7、横向摇摆力Q3。
Fj=(Gk1+Gk2)+k1k2Q1m+Q2j+Q4c+Q7+Q3
(8)
其中,式(8)中冲击系数k1=1.2,振动系数k2=1.2。
2)偏载急停制动工况,此工况下包含永久载荷Gk,偏载活载荷Q1p、紧急制动力Q2j、风载荷Q4c、温度载荷Q7、横向摇摆力Q3。
Fj=(Gk1+Gk2)+k1k2Q1p+Q2j+Q4c+Q7+Q3
(9)
其中,式(9)中冲击系数k1=1.2,振动系数k2=1.2。
4.2 容许应力值
根据《规范》,材料极限应力与其承受的最大应力比值为安全系数。重要的轴、销轴及Ⅰ级和Ⅱ级焊缝许用安全系数n≥5,其余构件许用安全系数n≥3.5,材料的极限应力σb=470 MPa,安全系数n=3.5时,最大许用应力:
[σ]max=σb/n=134.3 MPa
(10)
4.3 容许应力法有限元计算结果
在两种不同工况下,分别对轨道梁进行有限元分析,得到轨道梁在不同工况作用下的最大应力值,并与容许应力值进行比较。两种工况的有限元分析结果如图6所示。
由图6(a)可知,满载急停制动工况应力为123.6 MPa,由图6(b)可知,偏载急停制动工况应力为116.8 MPa,满载急停制动工况应力值最大,应力值为123.6 MPa,小于容许应力值134.3 MPa,应力安全余量为10.7 MPa。
4.4 竖向位移
满载急停制动工况时应力值最大,则对比极限状态法和容许应立法在此工况下的竖向位移,如图7所示。
由图7(a)可知,用极限状态法求得满载急停工况最大位移为12.011 mm,由图7(b)可知,用容许应力法求得满载急停工况最大位移为11.982 mm,可知应用两种方法求得最大位移相同。
4.5 极限状态法与容许应力法分析结果对比
通过在满载急停制动工况和偏载急停制动工况下,分别采用极限状态法与容许应力法对24 m轨道梁进行有限元分析,结果见表2。



表2 极限状态法与容许应力法结果对比
通过两种方法的有限元分析结果对比,最大应力工况均为满载急停制动工况,说明极限应力状态法同容许应力法对工况分析结果是一致的,但是极限状态法的安全余量高于容许应力法,且二者在最大应力值工况下的位移基本一致。
5 结语
轨道梁设计中存在应力、材料强度、载荷等变化的不定性因素,容许应力法将各种不定性因素影响,体现在安全系数的选取,单一的安全系数导致计算结果出现过分保守或者不安全的情况。极限状态法综合考虑了载荷系数、强度系数、构件重要性系数等因素,提高了设计的完整性和可靠性。采用极限状态法,对24 m轨道梁强度和刚度进行计算,并与同条件下采用容许应力法计算结果进行对比分析,得出如下结论:
1)采用极限状态法与容许应力法得出的最大应力工况是一致的,即均在满载急停制动工况下应力值最大,且在最大应力值工况下的刚度计算结果基本一致,说明极限状态法设计方法是可靠的,在旅游轨道交通中使用是适合的。
2)相同工况下,极限状态法载荷组合下得到的最大应力138.5 MPa,大于容许应力法载荷组合下得到的最大应力123.6 MPa,说明极限状态法的载荷组合方式比容许应力法更严格。
3)从表2列举的结果可知,极限状态法的极限应力大于容许应力法的许用应力,同时安全余量也高于容许应力法,说明采用极限状态设计法对材料强度利用较充分,而容许应力法设计较为保守。

