正交频分复用信号峰均比抑制技术研究

孙柏昶，李佳宣，张金波，李 倩

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081;2.北京理工大学 信息与电子学院，北京 100081;3.北京银河信通科技有限公司，北京 100084)

0 引言

正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术具有较高的频谱利用效率和抗多径衰落能力[1-3]。然而，由于OFDM系统是一个多载波系统，易产生较大的峰值功率[4-5]。随着子载波个数的增加，峰值产生的概率和幅值也随之增大，导致较高的峰均比(Peak to Average Power Ratio，PAPR)[6-7]，从而降低高功率放大器(HPA)的工作效率[8]，增加系统的运行成本。如果峰值功率进入功放的非线性区还会导致发送信号的非线性失真，影响系统的误比特率(BER)性能[9]。因此，OFDM系统需要采取相应的技术措施来降低发送信号的峰均比。

现有的PAPR降低技术主要可分为3类：信号畸变技术、信号编码技术和信号扰码技术[10]。信号畸变技术包括限幅法、压扩法以及峰值抵消波峰因子降低技术(PC-CFR)等，其计算复杂度较低，但会造成信号非线性失真，降低系统BER性能[11]；信号编码技术不会造成非线性失真，但是在选择合适的码字和解码的过程中计算复杂度较高，而且会降低系统的传输效率[12]；信号扰码技术包括选择性映射(SLM)算法[13]和部分传输序列(PTS)算法[14]等，此类方法不会造成非线性失真，但是需要额外传输边带信息，而且不能按照人为要求控制处理后信号的峰均比。

针对上述3种峰均比抑制方法的优缺点，本文将PC-CFR算法与PTS算法相结合，提出了一种联合改进的PTS-PC-CFR算法。仿真结果表明，所提算法可以有效控制信号的峰均比，相比PC-CFR算法明显降低了信号的非线性失真程度，优化了系统BER性能。

1 系统模型

1.1 离散复基带信号峰均比

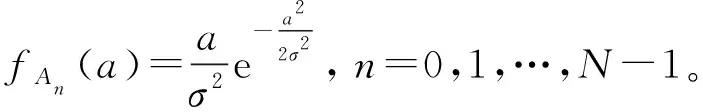
因此，一个OFDM符号其峰均比小于某一门限PAPR0的概率，即累计分布函数(CDF)：

(1)

根据CDF，可以得出一个OFDM符号其峰均比大于某一值PAPR0的概率，即互补累计分布函数(CCDF)：

CCDF(PAPR0)=1-CDF(PAPR0)=1-(1-e-PAPR0)N。

(2)

1.2 连续复基带信号峰均比

式(2)为采样率刚好满足采样定理时，OFDM信号PAPR的CCDF表达式。但此时采样点不一定包含连续信号的最大值，所以连续信号或过采样信号PAPR的CCDF并不满足式(2)。由于过采样信号的采样点之间具有相关性，统计特性很难直接计算，因此引入系数α对过采样信号的CCDF进行近似[17]：

CCDFOS(PAPR0)=1-(1-e-PAPR0)αN，

(3)

通常α=2.8时，结果与实际值最为相近。

1.3 复基带信号与实带通信号的PAPR关系

由于复基带信号的载波表示为ejωt，峰均比为1，实带通信号的载波表示为cos(ωt)，峰均比为2。实带通信号与复基带信号的峰均比存在2倍(3 dB)的关系。但这3 dB的差别在使用频谱仪CCDF测量功能对带通信号进行测量时并不能直接测出，且在考虑功率放大器的工作点相对1 dB压缩点的功率回退也并不考虑此3 dB的差别。前者因为频谱仪测量前会对信号进行正交下变频，测得结果仍然是复基带信号的峰均比；后者因为1 dB压缩点的定义是平均功率。

令载波角频率为ωc，OFDM信号正交上变频后的实带通信号xrf(t)表达式为：

xrf(t)=xI(t)cos(ωct)-xQ(t)sin(ωct)=

|x(t)|cos(ωct+φ),

(4)

由式(4)所示，由于载波频率远大于信号带宽，即ωc>>2πNΔf，|x(t)|可看作一个慢变的包络，因此可以近似认为max(|xrf(t)|)=max(|x(t)|cos(ωct+φ))≈max(|x(t)|)，所以上变频前后的峰值功率满足max(|x(t)|2)≈max(|xrf(t)|2)。

(5)

(6)

其中，PAPRrf为实带通信号的峰均比，PAPR为复基带信号的峰均比。由式(16)可验证实带通OFDM信号峰均比为复基带OFDM信号峰均比的2倍，即多出3 dB。

1.3.1 频谱仪CCDF测量

频谱仪也可以进行信号的CCDF测量，但使用频谱仪测量带通信号的CCDF时，测量结果会和复基带信号的CCDF相近，即无法体现出3 dB的差距。这是因为频谱仪在测量CCDF前进行了IQ解调和A/D采样，并非直接对带通信号进行采样测量，实际测量的CCDF是IQ解调后由I路和Q路的采样点组成的复信号CCDF结果，因此和上文中计算的复基带信号CCDF结果相近。

如果希望实际测量实带通信号的峰均比情况，需要使用高速A/D直接对带通信号进行采样，此时进行CCDF计算的结果便与xrf(t)的CCDF结果相同。需要注意频谱仪绘制的CCDF曲线讨论的是单个采样点功率与平均功率的比值大于某PAPR0的概率曲线，第1节讨论的CCDF曲线针对的是一个OFDM符号峰值功率与平均功率的比值大于某PAPR0的概率曲线。即前者的样本是一个采样点，后者的样本是一个OFDM符号。后者是前者关于一个OFDM符号所有采样点的积事件，需要注意区分。

1.3.2 功放功率回退和PAPR的关系

对于以OFDM为代表的多载波系统，在选择高功率放大器工作点时，通常使用功放的1 dB压缩点P-1回退复基带峰均比(分贝值)作为功放的工作点。功率放大器的输入信号是实带通信号，明确使用复基带信号x(t)的峰均比，还是使用实带通信号xrf(t)的峰均比作为功放工作点的回退依据是值得讨论的。实际上应使用复基带信号x(t)的峰均比作为功放工作点回退依据。

功放的1 dB压缩点P-1通常使用单音信号的平均功率进行标定，并非使用瞬时的峰值功率进行标定，因此这两个值是平均功率的概念，即功放输出正弦波的包络功率。在讨论功率回退时，回退的功率也应为实带通信号xrf(t)的包络峰均比。实带通信号的包络为|x(t)|，即复基带信号的模值，其峰均比等于复带通信号x(t)的峰均比，所以应使用复基带信号x(t)的峰均比作为功放工作点回退依据。

2 PTS-PC-CFR算法

针对传统PC-CFR算法EVM较高的问题，本文在PC-CFR算法的基础上，结合PTS算法，提出了PTS-PC-CFR算法。

2.1 PTS算法

2.2 PC-CFR算法

峰值抵消波峰因子降低(PC-CFR)算法[19]是一种通过限幅降低信号PAPR的方法，PC-CFR算法通过生成和原信号频谱相似的脉冲信号与原信号的峰值部分进行对消，将原信号的PAPR降低到目标值。PC-CFR算法主要分为4个步骤：峰值检测、计算峰值缩放因子、产生对消脉冲信号和峰值对消处理。

峰值检测根据I/Q信号计算OFDM符号s的平均功率和每个采样点的瞬时功率，由预设的峰均比门限值Tthreshold找出超过门限的采样点，并找出相应的峰值点sp=spi+j·spj。

计算峰值缩放因子计算步骤峰值点的相位φp=arctan(sp)以及超出门限的幅值(|sp|-Ath)，其中|sp|表示峰值采样点的幅值，Ath表示Tthreshold对应的幅度门限。峰值缩放因子可表示为η=(|sp|-Ath)·ejφp。

产生对消脉冲信号对消脉冲信号是PC-CFR算法的核心，该信号的频谱特征应该与OFDM原始信号尽量一致。在此可根据OFDM信号频谱形状产生一个原型对消脉冲信号cpulse，利用峰值缩放因子可产生最终的对消脉冲信号为η·cpulse。

峰值对消处理以峰值点为中心，将峰值点附近信号减去对消脉冲信号，即可完成峰值对消。

2.3 PTS-PC-CFR算法

PC-CFR算法具有良好的带外抑制性能，但是在处理QAM调制信号时信号失真仍然较大。PTS-PC-CFR算法将PTS算法与PC-CFR算法相结合。通过降低PC-CFR算法处理信号的峰均比、峰值对消的次数以及信号处理前后的失真程度，从而在同样的目标PAPR的情况下达到更优的EVM性能。算法流程如图1所示。

图1 发射机PTS-PC-CFR算法流程Fig.1 PTS-PC-CFR algorithm flow of the transmitter

接收机的基带信号处理如图2所示，基带信号进行定时同步和载波同步后，进行FFT将时域数据转换为频域数据，根据发射机给出的边带信息对每个分块中的频域数据进行旋转因子补偿，之后进行信道均衡、解调、译码等传统OFDM接收机处理。

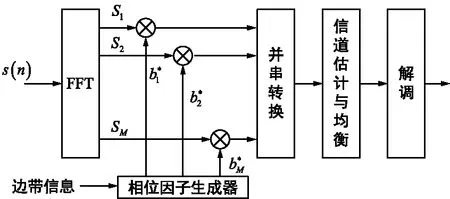
图2 接收机PTS-PC-CFR算法流程Fig.2 PTS-PC-CFR algorithm flow of the receiver

PTS算法是通过将子载波进行分块重组，使多载波信号相互叠加时彼此相位尽可能不同，从而降低峰值信号出现的概率，属于线性变换方法。PC-CFR算法是将超过阈值的峰值因子与对消脉冲进行抵消，使超过阈值的峰值因子降低到阈值以下，属于非线性变换方法，会引入一定的带内噪声。PTS算法和PC-CFR算法二者有一定的互补性，但在联合使用两种算法时，级联的顺序会严重影响整体算法的性能。如果采用PC-CFR-PTS方案，即先对信号进行PC-CFR处理，再进行PTS处理，需要对所有分块的时域信号进行PC-CFR的峰值对消，大大增加了计算复杂度，并且无法确定整体算法处理后信号最终的PAPR值为何值。如果采用PTS-PC-CFR方案，即先进行PTS处理，再进行PC-CFR处理，则信号经过PTS处理后，超过阈值的峰值因子减少，大大减小了PC-CFR算法影响的采样点数。PC-CFR每处理一个峰值，就需要进行一次脉冲对消，相当于对带内信号引入一次噪声，PTS-PC-CFR方案减少了PC-CFR处理的峰值，因此引入的带内噪声也明显降低，所以整体联合改进算法使用PTS-PC-CFR方案。

3 仿真结果及分析

为了验证PTS-PC-CFR算法降低PAPR的性能，图3给出了不进行峰均比抑制处理的原始信号、PTS-PC-CFR算法、PTS算法以及PC-CFR算法进行峰均比抑制的PAPR仿真结果。

图3 3种算法的PAPR抑制性能对比Fig.3 Comparison of PAPR reduction performance of three algorithms

图4给出了PTS-PC-CFR算法以及PC-CFR算法的EVM性能随目标PAPR的变化。本文仿真条件为子载波数N=128，子块数M=4，调制方式为16QAM，相位因子bm∈{1,-1}，过采样率L=4，对于PC-CFR算法流程峰均比抑制后目标峰均比为6 dB。

图4 EVM性能对比Fig.4 EVM performance comparison

由图3可以看出，PTS-PC-CFR算法的PAPR性能和PC-CFR算法比较接近，且优于PTS算法。PTS-PC-CFR算法和PC-CFR算法均能将信号PAPR降低到目标峰均比左右。PTS-PC-CFR算法相比PC-CFR算法，其EVM性能更加优秀，由图4可以看出，在同样的目标PAPR情况下，PTS-PC-CFR算法相比PC-CFR算法的EVM性能有明显改善，在目标PAPR为6 dB时改善约为2%。PTS-PC-CFR算法和PC-CFR算法均会对信号引入畸变，此畸变可被认为是一种随机噪声，畸变越大引入噪声越大，对误码率的影响越大。图5给出了PTS-PC-CFR算法和PC-CFR算法的误码性能随Eb/N0的变化，目标PAPR均为6 dB。

图5 PTS-PC-CFR及PC-CFR算法的误码性能对比Fig.5 Error code performance comparison between PTS-PC-CFR and PC-CFR algorithms

由图5可以看出，在同样目标PAPR的情况下，PTS-PC-CFR算法相比PC-CFR算法BER性能有明显改善，误码率在10-6处Eb/N0相差5 dB。并且PTS-PC-CFR算法的BER性能非常接近不进行信号畸变的理论极限性能，差距小于1 dB。结合其PAPR性能和EVM性能，说明PTS-PC-CFR算法具有良好的峰均比抑制性能。

4 结束语

本文主要讨论了基带复信号和带通实信号的PAPR关系，经过理论推导分析得出频谱仪测量的PAPR结果等于复基带信号PAPR，高功率放大器功率回退大小应和复基带信号PAPR相同。由于传统的PC-CFR算法在处理QAM调制信号时失真较大，提出了一种联合改进的PTS-PC-CFR算法。仿真结果说明，PTS-PC-CFR算法相比于PC-CFR算法在目标峰均比相同的情况下，具有更好的EVM性能和误码性能。