再解第45届俄罗斯数学奥林匹克竞赛试题

陕西师范大学附属中学 (710061) 李鑫明 张锦川

题目证明：对于任意ΔABC，不等式acosA+bcosB+ccosC≤p成立，其中a,b,c为ΔABC的三边，A,B,C分别为它们的对角，p为半周长.

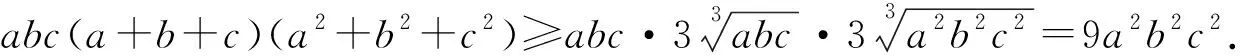
反思：本解法利用余弦定理将不等式中的三角函数转化成边长的式子，从而达到了不等式形式上的统一，接着利用均值不等式及舒尔不等式即可证明原不等式.

反思：本解法利用正弦定理将不等式中的边长转化成三角函数的式子，从而也达到了不等式形式上的统一，利用三角恒等变换将原式化简，最后利用詹森不等式即可得到原不等式的证明.

解法3：不妨设a≤b≤c，则有cosA≥cosB≥cosC，由排序不等式可得acosA+bcosB+ccosC≤acosB+bcosC+ccosA(1)，acosA+bcosB+ccosC≤acosC+bcosA+ccosB(2).(1)式加(2)式可得2(acosA+bcosB+ccosC)≤(ccosB+bcosC)+(acosB+bcosA)+(acosc+ccosA)即2(acosA+bcosB+ccosC)≤a+c+b，即acosA+bcosB+ccosC≤p.

反思：本解法并未将不等式中的边角统一化，而是结合射影定理和排序不等式，通过计算，将边角直接化为边，证明过程较为巧妙.