基于数据增强的小样本通信干扰识别技术

施育鑫，安 康，李玉生

(国防科技大学第六十三研究所，江苏 南京 210000)

0 引言

由于无线通信信道的开放性，无线通信信号容易受到人为有意干扰的攻击。人为有意干扰主要是指来自敌方的恶意干扰，是威胁通信生存能力的主要因素[1]。典型的有意干扰样式有单音干扰、多音干扰、窄带干扰及梳状干扰等。干扰方可以根据不同的干扰动机灵活地切换干扰样式，有针对性地破坏合法通信。因此，干扰识别作为通信抗干扰过程中的前置环节，为后续的抗干扰决策、抗干扰波形的选择提供先验知识，对通信抗干扰具有重要的意义。

在通信信号的调制识别中，其识别对象一般为合法通信用户的调制方式。合法用户的调制方式相对固定，持续发送时间长,发送信号结构更具有规律性，识别器更容易获取大量已标记的样本数据进行训练。文献[2]采用了基于深度学习的方法对常见的调制信号进行识别，表明基于大数据训练的深度学习在提高无线电信号识别的灵敏度和准确性上的优势。然而，在复杂的电磁频谱环境和敌我态势矛盾尖锐的战场环境下，干扰信号持续发送时间相对更短，干扰样式可能会不断切换，所在的信道条件更加恶劣，这使得基于大量已标记数据训练的深度学习方法的实施异常困难。此外，干扰识别作为抗干扰过程中的前置环节，需要尽可能低的计算复杂度，以保证干扰识别的实时性。例如，当干扰方施加了特定样式的干扰信号后，若干扰识别算法过于复杂，在很大的延时后通信方才能获取关于干扰信号的样式。此时，干扰方只需要在一段时间内更改干扰样式，即可使通信方的抗干扰措施失效。

因此，通信干扰的识别过程更适合建模为一个小样本识别问题，即通信干扰识别时，仅有少量的已标记干扰信号样本作为训练数据集。针对典型的干扰样式，常见的干扰识别方法有决策树[3]、支撑向量机及反向传播神经网络[4-5]等。其中，决策树方法基于多维空间的分段线性划分进行分类，但在有噪声情况下容易造成过拟合。支撑向量机与反向传播神经网络识别方法一般具有较高的复杂度，将带来较大的延迟。贝叶斯分类器采用因果推理的方式计算各类的概率，具有实现简单和计算方便的特点。在文献[6-7]中，利用常见的几种干扰特征作为训练集，使用朴素贝叶斯分类器进行干扰识别。然而，文献[7]指出当训练数据样本较小时(每类干扰的训练样本小于20个)，干扰分类器的稳定性较差。

小样本学习 (Few-Shot Learning,FSL) ，是近年来受到广泛关注的研究方向，被用于解决机器学习方法在训练集很小时出现性能不佳的情况[8]。小样本学习利用先验知识，可以快速泛化到只包含少数有监督信息的样本的新任务。在小样本学习中，数据增强(Data Augmentation)方法利用先验知识对训练数据进行增强，以提升训练过程的精度。在图像分类识别领域，通常使用平移、翻转、剪切、缩放及旋转等方式进行数据增强[8]。上述操作一般不会改变图像所属类别，因此其先验知识可以用于指导数据增强以产生更多的训练样本。但是，不同于图像识别，上述操作可能会使得待识别的干扰信号类别发生改变。因此，如何在小样本条件下寻找可行的先验知识进行数据增强是一个亟待解决的问题。

受小样本学习中数据增强方法的启发，本文研究了在贝叶斯分类器视角下小样本干扰信号识别可用的先验知识，并根据所分析的先验知识提出了两种贝叶斯分类器的数据增强算法，以解决贝叶斯分类器在小样本条件下的欠拟合问题。实验结果表明，所提的数据增强算法能够显著提高贝叶斯分类器在小样本条件下的识别准确率。

1 系统模型

为了实现干扰目的，恶意干扰机针对目标频段施加干扰，将调制的干扰信号发送到无线信道。当干扰机开始工作时，合法用户为了进行有效的抗干扰决策，首先进行信号接收和干扰识别。其接收到的采样信号可以表示为：

y(n)=J(n)+w(n),

(1)

式中,J(n)表示干扰信号，w(n)表示白噪声。y(n)=y(nTs)，Ts表示最小采样间隔。令每T时间内接收到的信号作为一组干扰样本数据，则每组数据可用向量形式表示为：

(2)

随后，合法用户首先对接收的时域信号y做归一化：

(3)

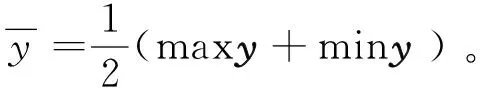
接着，对归一化的数据分散化，可得：

(4)

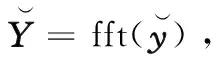
(5)

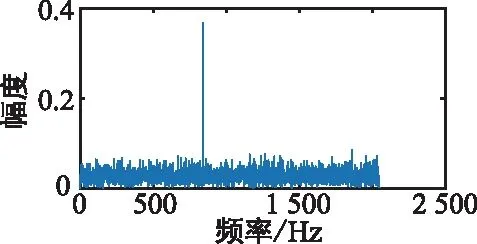
(a) 单音干扰

2 基于贝叶斯方法的干扰分类

接下来介绍如何建立基于贝叶斯方法的干扰分类器。图2给出了两种贝叶斯干扰分类器的训练过程。对于已标记的6种干扰信号计算对应的4类干扰特征后，可以获得带有标签的特征训练集。

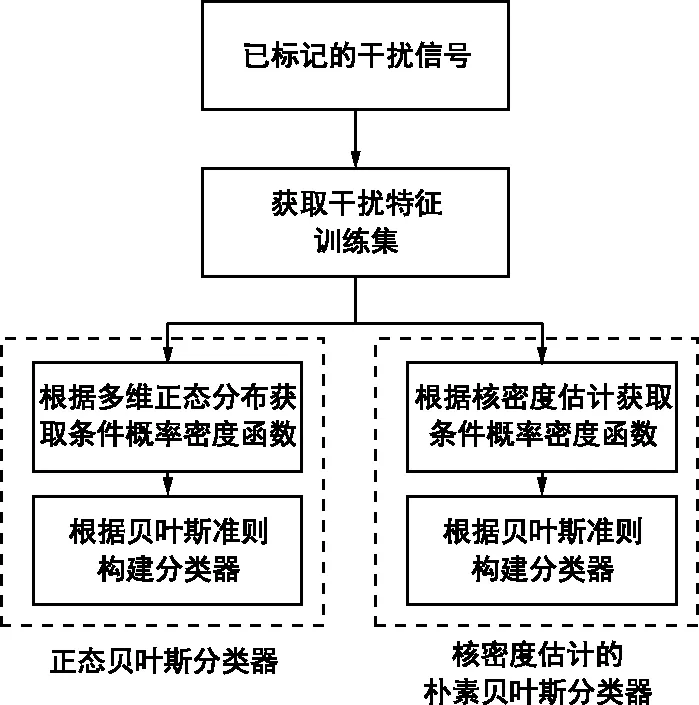
图2 两种贝叶斯分类器的训练过程Fig.2 Training processes of two Bayesian classifiers

在正态贝叶斯分类器中，假设4类干扰特征向量服从多维正态分布，其条件概率密度函数可以表示为[15]：

(6)

式中，x表示4类干扰特征组成的向量，n表示特征向量的维数，这里n=4；ci表示第i类干扰信号，i=1,2,…,6；μ表示均值向量，Σ表示协方差矩阵。

在识别过程中，贝叶斯分类器需要寻找具有最大后验概率的类，作为最后的分类结果。通过贝叶斯公式可以得到[15]：

(7)

由于p(ci)表示干扰出现的先验概率，在没有该信息时，对不同干扰下的p(ci)可以视为相等的常数。p(x)的在所有的干扰类下是相等的，因此式(7)的求解可以简化为：

arg maxp(x|ci)。

(8)

在正态贝叶斯分类器中，可以对其概率密度函数求对数函数，式(8)可以等价于：

(9)

其中，Gci=ln(|Σ|)+(x-μ)TΣ-1(x-μ)。即对于6类干扰信号，分别利用其估计的均值向量、协方差矩阵计算出其等价度量值Gci，寻找最小Gci的作为干扰分类结果。

在基于核密度估计的朴素贝叶斯分类器中，由于各个特征之间的密度函数被认为是无关的，因此有[7]：

(10)

通过核密度估计的概率密度函数，计算出在6类干扰下的p(x|ci)。对于最大的p(x|ci)，其干扰类型输出为干扰分类结果。

本节介绍了两种基于贝叶斯的干扰分类器的训练和干扰分类过程。然而，在小样本条件下，上述的训练过程将出现较大误差。接下来，分析了两类贝叶斯分类器中可利用的先验知识，并提出了基于先验知识的数据增强方法，以提高分类器的识别准确率。

3 基于先验知识的数据增强

3.1 正态贝叶斯分类器的数据增强

在正态贝叶斯分类器中，若训练样本过少，利用训练样本计算出的均值向量μ和协方差矩阵Σ与真实值将出现较大的误差。因此，需要通过增加训练样本以接近μ与Σ的真实值。受图像识别分类中数据增强方法的启发，图像在平移、翻转、剪切等数据增强的操作过程中，其实质分类不发生改变，但输入特征数据更加多样，这将有效提高识别器的泛化性能。因此，在干扰识别的过程中，数据增强需要达到两个目标：一是使在原干扰样本上增强的新样本，这样不会改变原有的干扰类型；二是使得数据增强后的干扰特征取值能够发生一定的变化，以产生有效的新训练样本。

根据上述分析，本文采用剪切的方式进行数据增强。图3以单音干扰为例，给出了接收到的干扰信号的单边谱数据剪切示意图。对于单边谱数据，可以剪切掉其两侧的部分数据，这是由于两侧数据往往不包含干扰信号，或者如宽带干扰和扫频干扰，即使剪去两侧的部分数据也不影响其干扰样式。依据上述先验知识，双侧剪切操作的实施步骤如算法1所示。

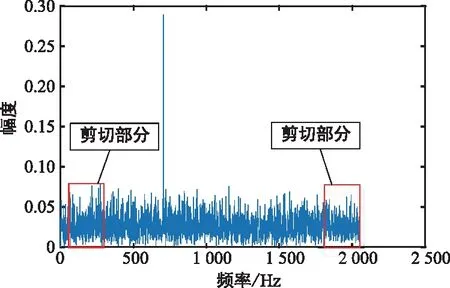
图3 基于剪切的数据增强Fig.3 Data augmentation based on shearing

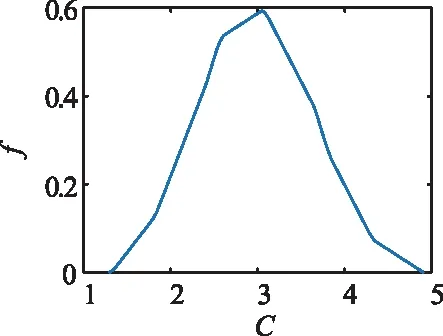
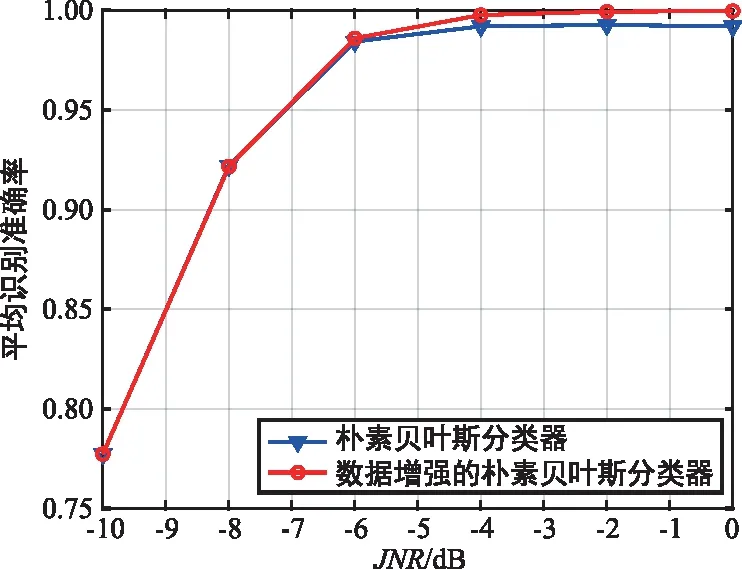
算法1 双侧随机剪切的数据增强算法输入:长度为N的信号单边谱Y︶s。剪切数据后样本扩增的倍数m。两端剪切的总长度2Ns。输出:数据增强后的特征训练集。实施过程:Fori=1,i

3.2 核密度估计的贝叶斯分类器的数据增强

在基于核密度估计的朴素贝叶斯分类器中，由于概率密度函数是利用小样本进行核密度估计生成的，可以直接生成概率密度函数观察失真程度。图4与图5给出了经过核密度估计后的概率密度分布。在训练过程中，图4每类干扰有5个已标记训练样本，图5每类干扰有100个已标记训练样本。显然，通过更多训练样本估计出的概率密度函数要更加接近真实的概率密度函数。比较图4与图5可以看出，训练样本数量为5的估计概率密度函数出现了严重失真的现象。特别是在特征Fse中，估计的概率密度函数出现明显不连续，这将带来较大的误差，使得干扰识别准确率将下降。此时，可以利用的先验知识是概率密度函数具有光滑而稳定的连续性。这是因为所采用的4类干扰特征反映了频域特征，不会随干扰的动态变化而出现概率密度函数的凹陷。

基于上述先验知识，提出了均值映射的方法，对已标记的特征训练集合进行数据增强，以提供更多有效的训练样本。不同于正态贝叶斯分类器中采用剪切的方法对单边谱进行数据增强后，再计算干扰特征的方法，均值映射数据增强方法的实施对象为特征训练集。均值映射的具体实施步骤如图4所示。

(a) 特征C的PDF

(a) 特征C的PDF

假设第i类干扰信号共有K个已标记的训练样本，则其训练样本的集合可以表示为：

(11)

定义训练样本的集合中元素的平均值为：

(12)

均值映射操作是以训练样本的均值为对称中心，对数据进行映射。对训练集第k个元素进行均值映射，可得映射数据：

(13)

因此，可以得到映射后的训练样本集合：

(14)

最后，将训练样本集合与映射后的训练样本集合合并，即完成的数据增强的过程。显然，通过上述数据增强的方法，可以将训练样本数增加一倍。随后，将新的数据集进行核密度估计，得到估计的概率密度函数输入朴素贝叶斯分类器，完成训练过程。

在核密度估计的朴素贝叶斯分类器中，没有采用剪切的数据增强技术，这是由于剪切产生的新特征值与原接收信号计算出的特征取值差异不大，因此这种数据增强的方式无法解决核密度估计时训练样本过少，导致概率密度函数估计失真的问题。通过均值映射一方面能够直接获取新的特征训练集，保证新的特征训练集与原训练集具有相同的均值，避免对均值估计带来额外的误差；另一方面，通过均值映射能够使特征取值的分布更加均匀，使得小样本条件下的核密度估计的失真问题得到缓解。

4 仿真实验结果

仿真参数设置如下：接收端的采样率为Fs=2 kHz，每组接收信号的时间T=2 s。由于每组接收信号有4 000个采样点，采用FFT长度为Nfft=4 096，取单边谱后长度为N=2 049。单音干扰和窄带干扰的中心频率点在50～600 Hz范围内随机设置；多音干扰的频率点数目在10～15的整数中随机设置，功率为0.9～1.0之间的随机变量，服从均匀分布，相邻频率点之间的间隙为40 Hz；宽带干扰是由加性高斯白噪声利用Kaise窗的低通滤波器产生的；对于梳状干扰，将4或5个窄带干扰组合在一起，相邻干扰之间的间隙设置为100 Hz；对于扫频干扰，扫频速率和初始频率分别随机设置为0～500 Hz/s和50～100 Hz。

4.1 数据增强的正态贝叶斯分类器

图6给出了正态贝叶斯分类器与所提数据增强的正态贝叶斯分类器的平均识别准确率比较，其中每种干扰的训练样本数K=5。在所提数据增强的贝叶斯分类器中，增加的新训练样本数与原样本数的比值为m=1，即每种干扰特征的训练样本扩增到10个。两端数据剪切长度Ns=20，满足Ns<

图6 正态贝叶斯分类器与数据增强的正态贝叶斯分类器的 平均识别准确率比较Fig.6 Comparison of average accuracy of classical normal Bayesian classifier and the proposed data augmentation aided normal Bayesian classifier

图7为数据增强方法在不同的新样本数条件下进行训练对平均识别准确率的影响。固定Ns=20，分别设置m=1，4，10。可以观察到，m值的提高会轻微地提高平均识别准确率，但提高的效果并不明显。

图7 数据增强的正态贝叶斯分类器在不同m值下的 平均识别准确率比较Fig.7 Comparison of average accuracy of the proposed data augmentation aided normal Bayesian classifier with different m

图8给出了数据增强的正态贝叶斯分类器在不同Ns值下的平均识别准确率比较。可以发现，增大Ns值对平均识别准确率的提高并没有显著帮助。并且当Ns=200时，准确率有所下降，这是因为剪切部分过程可能产生损伤的干扰信号，这类信号引入训练可能会导致错误的学习结果。

图8 数据增强的正态贝叶斯分类器在不同Ns值下的 平均识别准确率比较Fig.8 Comparison of average accuracy of the proposed data augmentation aided normal Bayesian classifier with different Ns

4.2 数据增强的核密度估计朴素贝叶斯分类器

图9～图12为所提均值映射的数据增强方法在不同训练样本数量下，对朴素贝叶斯分类器的平均识别准确率的影响。

图9中当训练样本数为5时，所提出的数据增强方法能够显著提高干扰的平均识别准确率，这表明了所提方法的有效性。图10与图11中均值映射的数据增强方法能够在JNR≥-6 dB的范围内提高平均识别准确率。

图9 平均识别正确率比较(训练样本为5)Fig.9 Comparison of average accuracy (5 shots)

图10 平均识别正确率比较(训练样本为10)Fig.10 Comparison of average accuracy (10 shots)

图11 平均识别正确率比较(训练样本为20)Fig.11 Comparison of average accuracy (20 shots)

图12中，数据增强在低JNR区域降低了平均识别准确率。这是由于50个训练样本已较为充分地减小了核密度估计带来的误差。此时因为均值映射时默认数据是沿均值对称分布的，而实际干扰特征的概率密度函数不一定沿均值对称分布。因此这样的假设带来的误差相比核密度估计误差成为了当前主要误差来源，造成了平均识别准确率的下降。

图12 平均识别正确率比较(训练样本为50)Fig.12 Comparison of average accuracy (50 shots)

5 结论

本文研究了小样本条件下两类贝叶斯分类器的数据增强通信干扰识别技术，通过数据剪切和均值映射两种数据增强方式，在小样本训练条件下能够显著提高正态贝叶斯分类器与核密度估计的朴素贝叶斯分类器的平均识别准确率。理论分析与仿真结果表明，数据增强技术能够利用先验知识，补偿小样本训练带来的欠拟合问题。在后续研究中，可以考虑利用数据增强与半监督学习相结合的方式进一步扩增已标记训练数据集，帮助解决小样本条件下的欠拟合问题，以进一步提高对干扰的识别准确率。