铁路重载货车轮对弹性振动及其动态影响

刘鹏飞 ，刘红军 ，高 昊 ，任尊松 ，张凯龙

（1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室, 河北 石家庄 050043；2.石家庄铁道大学机械工程学院, 河北 石家庄 050043；3.北京交通大学机械与电子控制工程学院, 北京 100044）

重载货车是我国重载铁路的重要装备，当前30 t轴重重载技术已开始成功运用.轴重的增加带来的轮轨磨耗、轮轨动态相互作用等问题十分突出，特别是货运提速对重载铁路的安全运营提出了挑战.在车辆系统动力学研究中，通常把车辆结构及其走行部件简化为刚性体.刚性体轮对模型具有集中质量和集中转动惯量，且只有6个刚性自由度，它与无质量钢轨作用，其有效频率只能达到30 Hz左右[1]，无法反映结构弹性振动对轮轨动态作用力及车辆性能的影响，无法表达出轮对存在的弹性变形以及分布质量情况，有必要引入弹性多体动力学理论将重载车辆的轮对考虑为柔性体后进行仿真，以更加切合实际.

针对轮对弹性振动及其动力学影响，国内外学者开展了广泛深入的研究.Peng等[2]研究了机车轮对柔性对车轮多边形化发展的影响，指出轮对的柔性在满足某些先决条件下，对车轮多边形化有一定的影响；Baeza等[3]给出了3种基于欧拉方法的弹性转动固体动力响应计算公式，适用于固体与非旋转结构相互作用的研究.采用类似方法，柔性体旋转效应对轮轨力的影响也由崔潇等[4]进行了讨论.Fourrie等[5-6]基于有限元弹性轮对建模技术，对钢轨波磨产生机理、轮轨滚动噪声问题等进行了研究.李国芳等[7-14]针对考虑柔性轮对的整车车辆动力学建模、轮轨伤损及动力学性能分析等问题，从轮对弹性振动的曲线通过性能影响[7]、运动稳定性的影响[8]、直线电机车辆动态响应的影响[9]、多边形的产生机理及高频振动特征[10-11]、车轮扁疤的冲击振动现象[12-13]、轮轨接触几何参数与轮轨磨耗关系[14]等进行了多方面论述.

相关柔性轮对的研究以客运车辆为主，针对重载货车轮对弹性振动问题研究还鲜有涉及.事实上，货车也正向轻量化发展，以降低自重、增加载重，其中轮对属于簧下质量，也是轻量化设计的对象之一，作为基本的走行部件，承担着更大的载荷，对货车的动力学性能影响至关重要，轮对弹性振动及其动态影响对于重载铁路车辆装备设计具有重要意义.鉴于此，本文基于多体系统刚柔耦合动力学分析方法，针对新型30 t轴重重载货车，开展考虑轮对弹性振动的重载货车动力学性能的研究，为重载铁路货车动力学仿真分析和动态性能评估提供理论依据和应用参考.

1 柔性轮对运动的数学描述

图1为重载货车轮对模型，其绝对参考系设为O0-X0Y0Z0.在描述轮对柔性旋转运动中，引入相对参考系O1-X1Y1Z1，该坐标系与车轮的运动状态相同，但与绝对坐标系（地面坐标系）始终保持平行，并且O1始终在轮对质心处，点P和P‘分别为轮对变形前、后某一点的位置状态，变形后，柔性体上点P‘在O0-X0Y0Z0坐标系的位置向量为uP，X1轴为轮对前进方向，在直线轨道上，Y1轴方向始终为初始时刻车轴横向，Z1轴方向始终垂直于轨道平面.两参考系原点的相对位置为r1，柔性体上任意点P在绝对坐标系O0-X0Y0Z0的位置向量为r，u为未变形状态下点P恒定半径矢量，u‘为点P变形后弹性位移，相对坐标系O1-X1Y1Z1的位置向量为u+u‘，则r如式（1）所示.

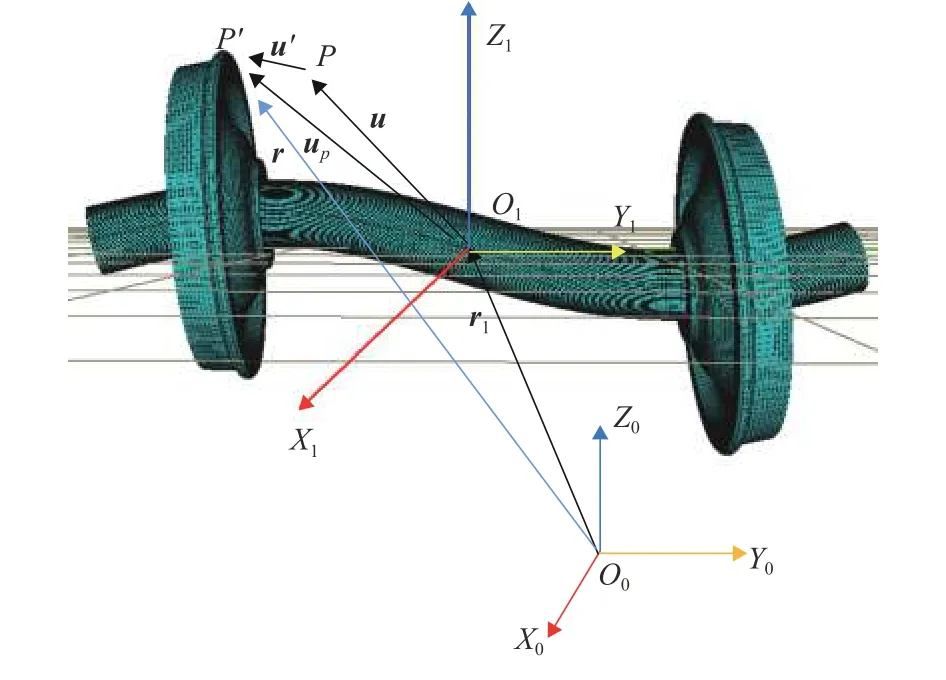
图1 柔性体空间描述Fig.1 Space description of flexible body

式中：A01为参考系转动时的坐标变换矩阵，如式（2）所示，其中θ0～θ3为欧拉四元数，由相对坐标系的旋转位置确定.

用模态振型叠加表示点P微小的弹性位移为

式中：HP∈RN×H为在模态集中提取出与点P相关的模态矩阵，N为有限元模型自由度的个数，H为所选模态阶数；q(t)∈RH×1，为模态坐标，t为时间.

在具体的弹性多体系统动力学中，可以通过铰与力元连接刚性体和弹性体，以确定物体间的相对运动关系，综合结构的弹性位移、刚体位移、振动速度等确定受力特性，并使用虚功原理或达郎贝尔原理，建立多体系统动力学方程为

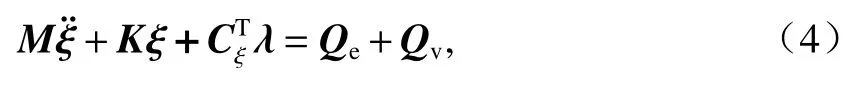
式中：M为质量矩阵；K为刚度矩阵；ξ为系统坐标向量；Qe为外力向量；Qv为离心力向量；Cξ为矩阵；λ为拉格朗日乘子向量.

通过对式（4）进行直接数值积分，可求得系统动态响应.

2 重载货车刚柔耦合动力学模型

2.1 柔性轮对建模

基于上述原理，本文建立了轮对的柔性模型，并进行了整车刚柔耦合系统的集成.首先需要注意的是，实际重载货车车轴及车轮型式随轴重不同而有所变化，25、27、30 t轴重转向架分别装用 RE2B、RE2C、RF2型车轴，如 30 t轴重的 DZ4、DZ5型转向架车轮的结构均采用HFS或HFZ型[15]，材料为LZ45CrV的车轴钢[16]，车轮名义滚动圆直径也由传统的840 mm增大到了915 mm，有助于增大轮轨接触面积，降低轮轨接触应力.根据 TB 1010—2016[17]规定，确定了车轮和车轴的具体几何形状和结构参数，如图2所示，车轮踏面为经典的LM型踏面，车轮采用S形辐板，这有利于增大车轮的结构弹性，车轴为变截面实心阶梯轴，其中在轮座处的直径最大，以满足轮轴配合处高承载能力的需求.车轮与轮轴间以压装的形式通过过盈配合实现静连接.

根据图2所示轮、轴结构，建立了轮对三维几何模型和有限元模型，如图3所示.在有限元模型中，轮对采用Solid185三维实体单元进行离散处理，材料泊松比 0.3，弹性模量 210 GPa，密度 7800 kg/m3，模型共计约30万个单元，32万个节点.实际结构中，车轮和轮轴采用过盈配合，在计算轮对模态时，考虑的是轮对结构的宏观振动问题，整个结构发生总体的弹性变形，为此可将车轮和轴视为一个固结整体，忽略轮、轴间过盈配合关系.

图3 轮对几何及有限元模型Fig.3 Geometric structural and finite element model of wheelset

基于轮对的有限元模型，提取其质量矩阵、刚度矩阵后，把柔性体模型与多刚体动力学系统实现集成，进而求解出轮对弹性体自由模态.本文基于UM动力学软件开展建模工作，其步骤如图4所示.

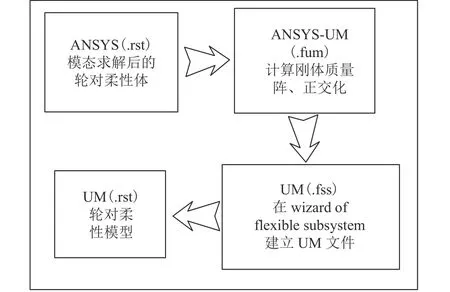
图4 基于 UM 的柔性轮对集成方法Fig.4 Integrated method of flexible wheelset based on UM

对于柔性轮对轮轨接触问题 （图5），由于轮对和钢轨本身具有较大的刚度，轮轨接触力又通常集中在很小的一个区域，即使接触点位置和相对速度发生很小的变化，都会引起接触力发生大的变化.因此柔性轮对建模时，通过自动插值找到任意时刻轮轨接触点所在踏面网格接触单元，再将该轮轨力等效分解作用于单元网格节点，亦即实现了轮轨力通过网格面、节点传递到柔性体的动态过程.

图5 轮轨接触特性的插值计算Fig.5 Interpolation calculation of wheel-rail contact feature

2.2 重载货车动力学建模

货车中存在大量的摩擦元件，这是发挥减振作用、提供回转阻力的关键，也是动力学建模的核心.其中，心盘及斜楔等摩擦元件统一考虑为摩擦-接触力元特性，其计算方法是利用线性黏弹性模型计算接触面的法向接触正压力Np（式（5）），再通过阻尼带宽法求解摩擦面摩擦速度瞬变过程中的切向滑动摩擦力Fμ（式（6）），通过力的分段数学描述，保证了摩擦力变化的连续性.

式中：kc和dc分别为接触刚度和接触阻尼；δ为接触面侵入量；μ为动摩擦因数；v0和vs分别为临界滑动速度和相对滑动速度在接触面上的投影.

常接触弹性旁承装置则根据其结构及受力特点可简化成如图6 （a）所示模型，C点为力作用点.将旁承磨耗板简化为无质量刚体，弹性旁承体简化为弹簧-阻尼模型，为了限制旁承产生过大的压缩量，导致回转摩擦力矩过大，在旁承上设置了一个滚子，所以在建模时将模拟弹性旁承的弹簧设置为两级刚度，如图6（b）所示，将旁承磨耗板与滚子之间的垂向间距设置为5 mm，弹性体垂向刚度为2.2 MN/m.

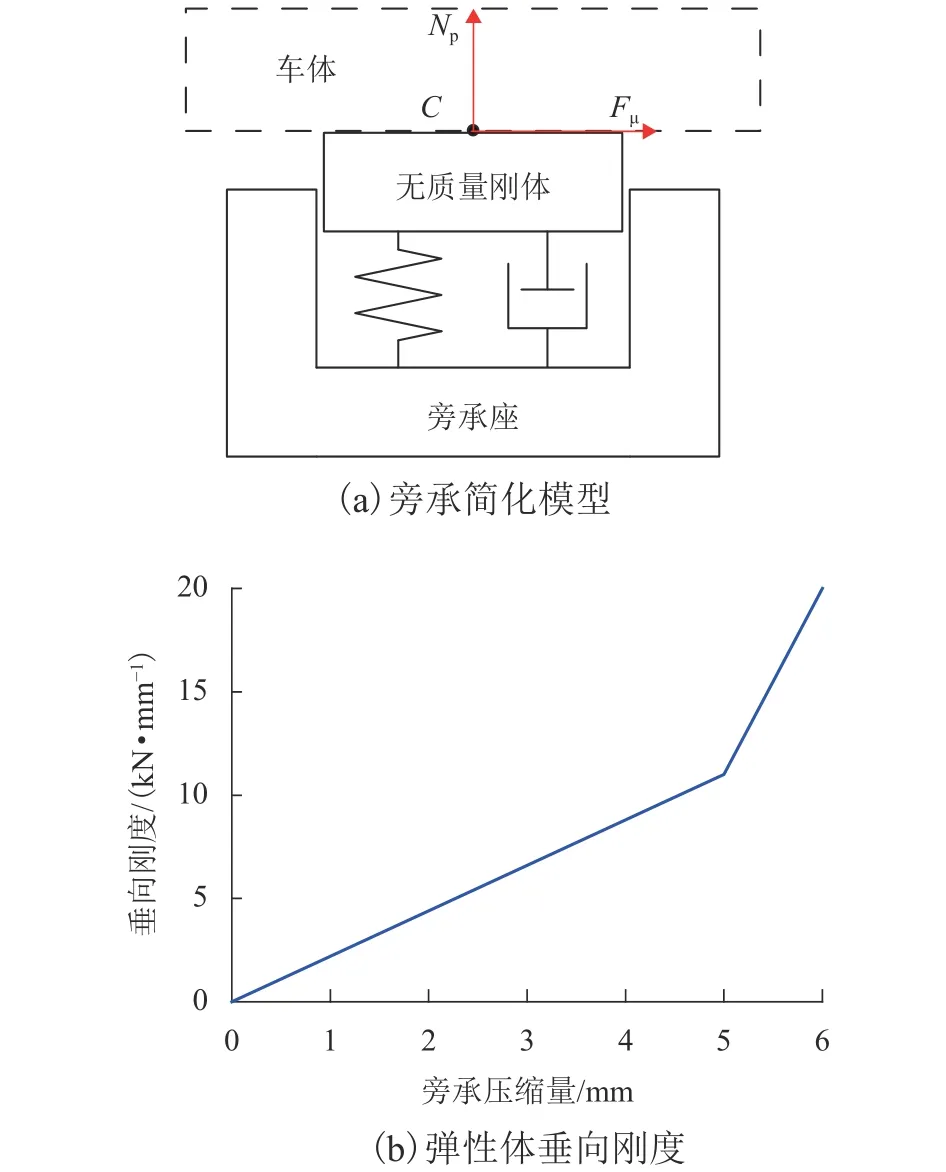
图6 旁承建模Fig.6 Modelling of side bearing

考虑柔性轮对后，重载货车动力学模型的拓扑结构如图7所示，图中，DOF为自由度（degree of freedom）.图8为建立的整车动力学模型，除轮对外，其余部件均采用刚体建模.另外，轨道的弹性振动对于重载机车车辆的动态行为也有影响[18-19]，为考虑这一因素，本文中轨道模型采用无质量钢轨，轨下则将轨道结构简化为考虑扣件垂向和横向的弹簧-阻尼系统.

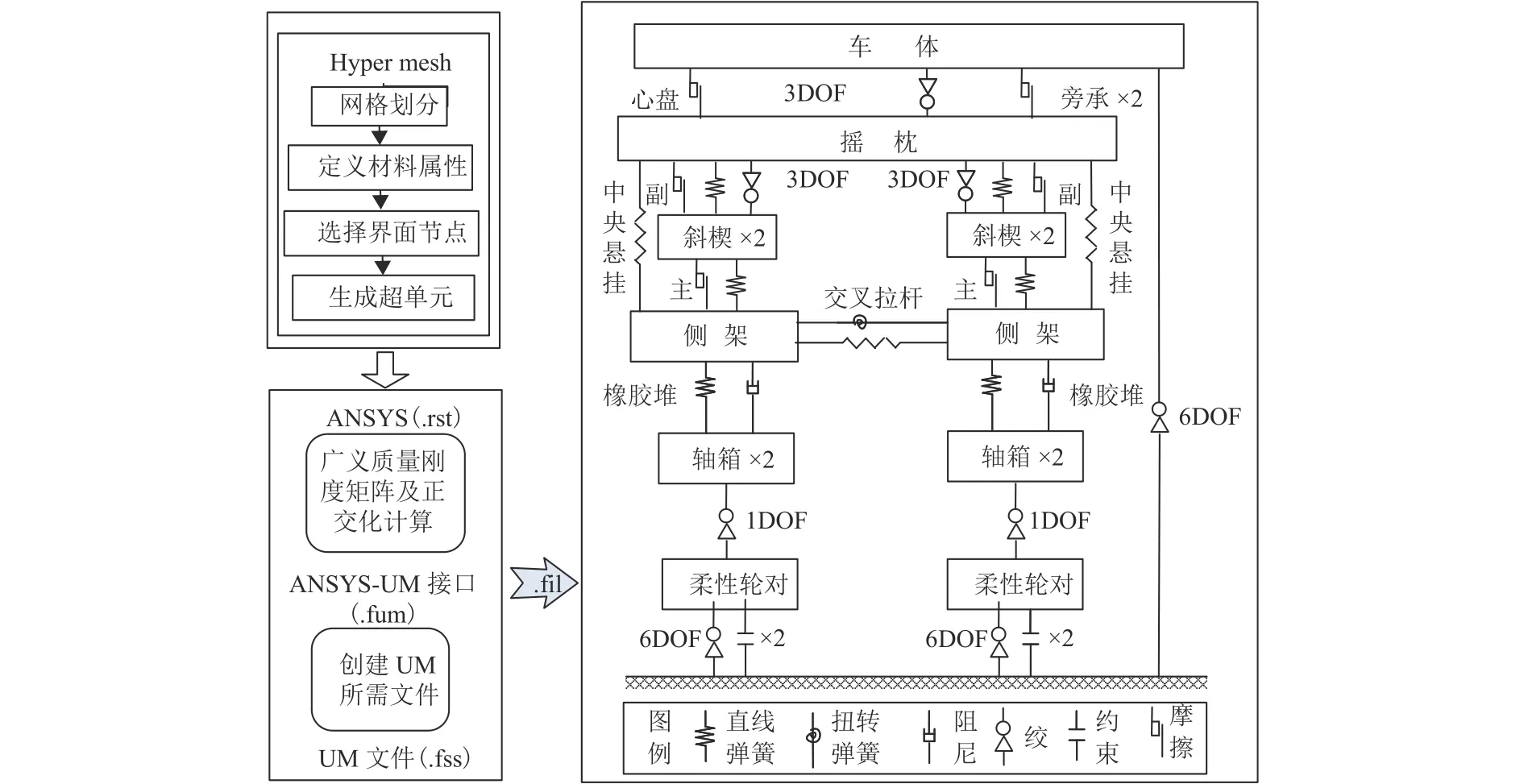
图7 柔性轮对建模及半车拓扑关系Fig.7 Modelling of flexible wheelset and topology relation of half vehicle

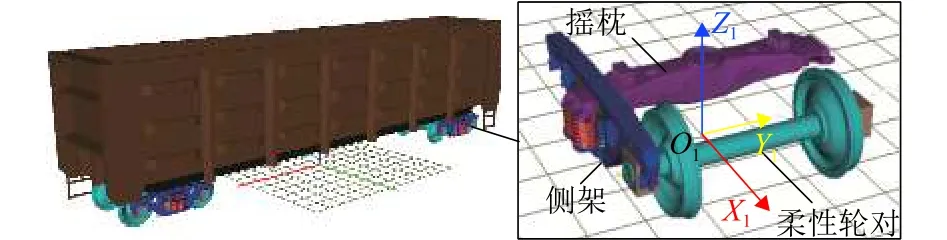
图8 货车刚柔耦合动力学模型Fig.8 Rigid-flexible coupling dynamic model of wagon

文献[20]针对摩擦斜楔减振装置的摩擦特性进行了试验和建模分析，参考该文献的试验参数、结果，采用多体动力学建模方法建立了同等参数的转向架模型，验证建模方法的准确性.车辆为重车工况，中央悬挂弹簧设置垂向为固定刚度，仿真结果如图9所示，摩擦减振器显示出明显的迟滞特性，摇枕载荷和垂向位移的幅值与文献[20]结果基本吻合，说明建模方法是正确的.

图9 摩擦减振器载荷-挠度曲线Fig.9 Load-deflection curve of frictional damper

此外，后续仿真中，对于轮轨激励，需能够激发轮对的中高频弹性振动模态，为此在轨道不平顺中应考虑短波成分.本文在传统的三大干线轨道不平顺基础上叠加了0.1～1.0 m波长的短波随机不平顺，采用基于石太线实测不平顺的拟合功率谱密度函数，由式（7）表示[18]，经过快速傅里叶反变换（IFFT），可将其转换为数值求解所需的空间样本，如图10所示.

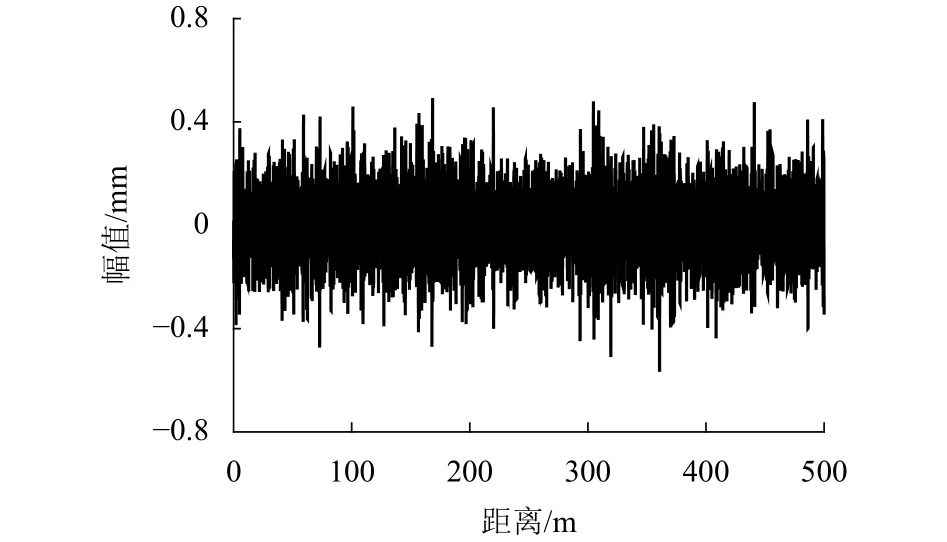
图10 短波随机不平顺Fig.10 Short-wave random irregularity

式中：f为空间频率，1/m.

3.1 柔性轮对的约束模态

相较于自由边界，实际轮对两端与轴箱连接，从而形成了约束效应.模态分析时，选取轮轴端部回转中心线上的点为界面节点，此处也是一系悬挂柔性约束点，在该点处释放绕轮轴方向的转动自由度，并模拟装配状态的约束情况，从而得到了约束条件下的振动模态与固有频率.车辆宏观动力学行为的主要能量集中在中低频，所以选取了300 Hz以下不同频率的约束模态，如图11所示.约束状态下，轮对的弹性振动模态主要表现为：轮对的扭转振动（98.8 Hz）、轮对的一阶弯曲振动（57.3 Hz，轮轴的弹性弯曲）、二阶弯曲振动（172.2 Hz，左右车轮的反向相对错动）和三阶弯曲振动（295.2 Hz，轮轴弹性弯曲与车轮反向相对扭转）.

图11 约束模态振型及相应的频率Fig.11 Constrained mode shapes and frequencies

3.2 轨道随机不平顺下的振动响应

使用上述建模方法分别建立了多刚体模型和轮对为柔性体的刚柔耦合模型，以直线线路为运行考核工况，运行速度为80 km/h，不平顺激扰下轮对的横向与垂向加速度时域响应如图12所示.从图12可以看出：不同建模方式对轮对的横向加速度影响不大，均在 ±2 m/s2的范围内波动；但刚体模型得到的轮对垂向加速度要大于柔性体模型，其幅值分别对应7.5 m/s2和 6.9 m/s2，表明柔性轮对的弹性变形一定程度上缓和了轮对垂向振动.

图12 轮对的振动加速度时间响应Fig.12 Time responses of wheelset acceleration

进一步，从频域响应的角度进行比较，将时域动态响应进行快速傅里叶变换（FFT），从而得到轮对的横向与垂向加速度频谱特性，如图13所示.就横向振动而言，1～3 Hz范围内柔性轮对振动幅度略高于刚性轮对，在20～100 Hz的频率，柔性轮对的振动幅值略小于刚性轮对的振动量；对于垂向振动，频率在1～20 Hz时，两种建模方式下垂向加速度频谱特性变化趋势大体一致，在大于20 Hz时两种模型的频谱幅值相差较大.结合3.1节的约束模态结果可知，柔性轮对的振动能量峰值分别对应其约束模态的垂向振动的自振频率，说明轮对的刚性建模放大了轮对处垂向加速度的值，轮对的弹性变形则能够对中高频振动起到一定的缓冲作用.

图13 轮对振动加速度频域响应Fig.13 Frequency responses of wheelset acceleration

4 蛇行运动稳定性分析

4.1 非线性临界速度比较

非线性临界速度是评价铁道车辆运动稳定性的重要指标，而该值的确定又与车辆的分叉形式有关.根据以往研究[21]，铁路货车由于存在大量的摩擦力元，非线性特性及动态响应规律极为复杂，实际临界速度与外界激扰、线路条件有关，轨道激扰幅值越大，稳定性就越差.鉴于此，在线路50 m处分别设置波长为 22、25、28、30 m，幅值均为 18 mm的方向不平顺，以模拟不同程度激扰，如图14所示.当车辆以不同速度通过时，观察轮对横移量是否收敛，以确定车辆的临界速度.不同工况下的临界速度统计结果如图15所示，两种模型的临界速度均随着波长的增加呈非线性增加，且刚柔耦合模型的临界速度要低于多刚体模型，降幅在3～8 km/h左右，体现了不同程度的外界扰动对车辆振动的激发程度有所差异.

图14 不同的外界激扰Fig.14 Different outer excitations

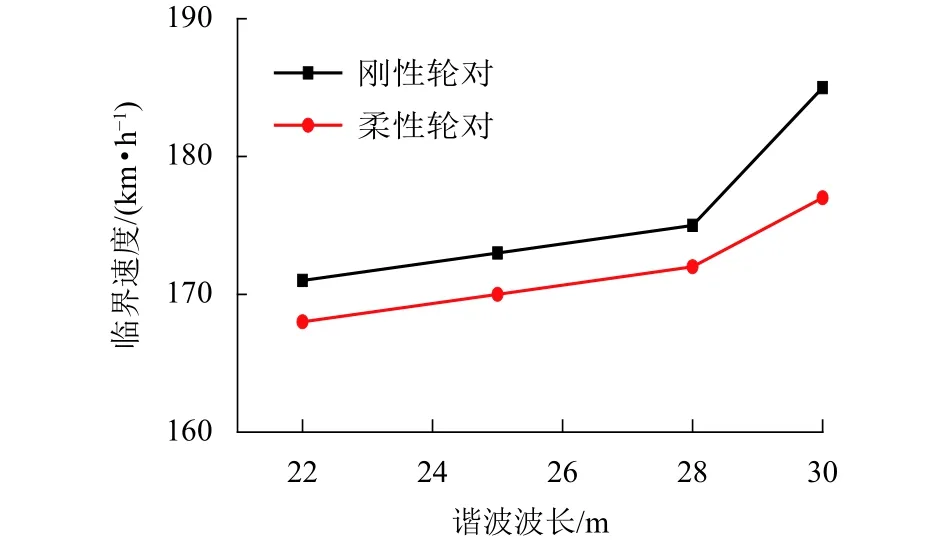
图15 弹性与刚性轮对的车辆临界速度Fig.15 Critical speeds of vehicle with flexible and rigid wheelsets

4.2 车辆实际临界速度的比较

铁道车辆实际临界速度的确定方法是：在轨道上施加一段运用线路轨道谱，使整个系统的振动被激发，然后使车辆系统在平直无不平顺的轨道上运行，当系统的响应不再衰减到平衡位置而是趋于稳定的极限环时，则此时的速度即为车辆临界速度[18].为了准确地反映车辆的实际临界速度，选取2.3节不平顺的100 m作为轨道激扰，使车辆在通过激扰时处于充分振动状态，从而分析轮对横向运动来确定其临界速度.通过分析图16（a）第一位轮对横向运动的时程响应可知：当多刚体模型的速度为150 km/h时，其波形出现振荡后衰减，故此速度下收敛；而速度为151 km/h时，波形持续振荡，故此速度下发散.所以多刚体模型的非线性临界速度是150 km/h，同理通过图16（b）可知：刚柔耦合模型的临界速度为136 km/h.

图16 一位轮对横向位移时间历程Fig.16 Time history of first wheelset later displacement

通过改变速度，观察系统响应特征，便可直观确定出刚柔耦合模型的非线性临界速度为136 km/h，较多刚体模型（150 km/h），下降了约 9%.这是由于在运行过程中，轮对通过结构的柔性变形，降低了轮轨之间的约束能力，导致临界速度下降.

5 动态曲线通过性能比较

为了研究轮对刚柔建模对其曲线通过性能的影响，设置了曲线运行工况.根据 TB 10098—2017[22]规定，重载铁路平面最小曲线半径不应小于800 m，继而设置车辆通过800 m半径曲线，曲线超高100 mm，缓和曲线长度100 m，分别以轮轨横向力、轮轨垂向力、脱轨系数、轮重减载率4类指标评判车辆的曲线通过性能.

图17给出了两种模型以90 km/h速度下一位外轮的轮轨横向力和垂向力响应.响应规律上看，两种模型的主要差异出现在圆曲线段，特别是较大幅值的横向力波动，相对于轮对的柔性体建模，进入曲线后轮轨力降低约10%.所以在建模时把轮对考虑成刚体时会过高估计的轮轨动力作用水平，也从侧面说明，轮对的弹性变形能够缓和轮轨间刚性冲击，利于其曲线通过，这是刚性模型无法反映的.

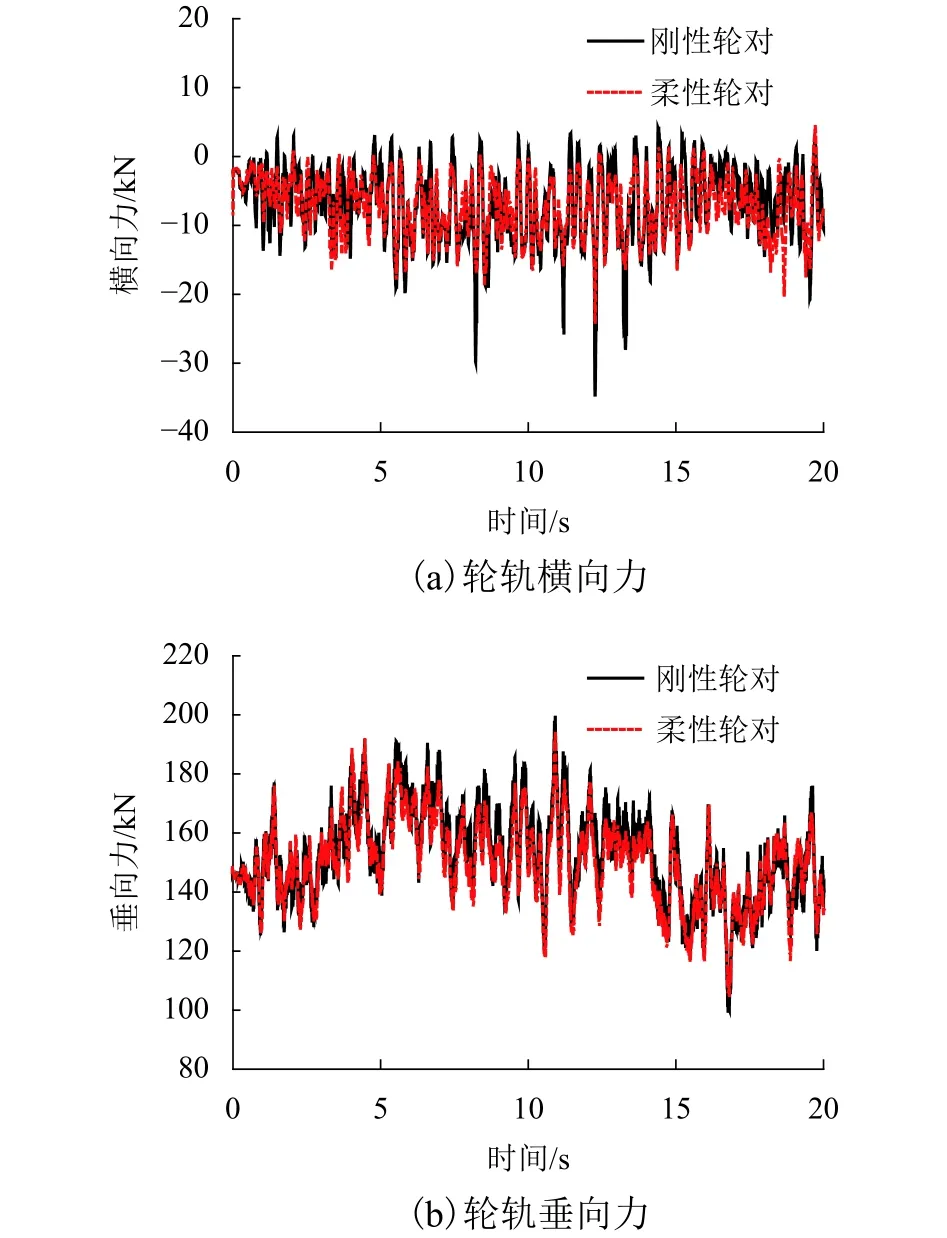
图17 一位轮对外轮轮轨作用力Fig.17 Outer wheel-rail forces of first wheelset

此外，从量化统计的角度对比研究两种模型不同速度下的曲线通过性能.选取5种不同的速度，对两种模型一位轮对外轮动力学指标最大值进行统计，各类曲线通过性指标统计如图18所示.通过计算对比可知，两种模型的横、垂向力以及脱轨系数都随速度的增加呈增大的趋势，但增长幅度不同，在60～100 km/h速度范围内，刚体模型对应的轮轨横向力、轮轨垂向力、脱轨系数和轮重减载率分别变化了 8 kN、30 kN、0.03、0.2，相应的刚柔耦合模型的对应动力学指标分别增大了 5 kN、30 kN、0.01 和 0.3.总体而言，刚柔耦合模型的轮轨横向力相对于多刚体模型约降低了13.7%，轮轨垂向力约降低了2.4%，脱轨系数较多刚体模型约降低10.9%，轮重减载率相差微弱，不到0.03.

图18 刚体与柔性轮对安全性指标比较Fig.18 Safety index comparisons between rigid and flexible wheelsets

综合以上分析，对于重载货车，轮对的刚性与柔性建模，主要区别体现在轮对20 Hz以上的振动有差异，特别是垂向动态响应上.轮对采用刚性建模时会过高估计车辆的非线性临界速度和通过曲线时的轮轨动态作用力.导致上述差异的本质原因在于，柔性轮对通过轮对结构的弹性变形，可以缓冲一部分中高频振动能量，另外反映了实际结构中存在的轮轴弯曲、车轮变形等对轮轨接触所产生的影响，降低了轮轨间的刚性约束效应，因而与基于轮对刚性假设的相应结果表现出一定差异.

6 结 论

针对30 t轴重重载货车轮对结构，建立了轮对柔性体有限元模型，进一步将其集成于多刚体系统中，建立了考虑轮对柔性的货车刚柔耦合动力学模型，并与刚性轮对模型进行了对比，得出以下结论：

1）轮对刚性和柔性建模主要影响20 Hz以上的中高频振动响应，刚性建模方法会高估轮对的振动量级，特别是垂向振动，在20 Hz以下两种建模方式对轮对振动影响微弱.

2）轮对为刚体的重载货车动力学模型的非线性临界速度较刚柔耦合模型高出约9%，说明柔性轮对的变形，降低了轮轨之间的约束能力，能够导致临界速度下降.

3）通过小半径曲线线路时，柔性轮对在一定程度上改善了车辆的曲线通过性能，刚柔耦合模型的轮轨横向力相对于多刚体模型约降低了13.7%，轮轨垂向力约降低了2.4%，脱轨系数降低10.9%，轮重减载率相差微弱，不到0.03.由于柔性变形，实际轮对结构能够缓冲一定的轮轨动态相互作用，轮对的刚体建模方法无法反映这一特点.

致谢：石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室自主课题（ZZ2021-10）.