染色石膏颗粒一维压缩破碎与形状演化

于际都，刘斯宏，沈超敏，毛航宇

(河海大学水利水电学院，江苏 南京 210098)

颗粒破碎在堆石坝工程中非常常见，严重的颗粒破碎可能导致坝体沉降过大和不均匀变形。颗粒粒径、级配、形状、堆积密度、岩性以及环境因素等均会影响颗粒破碎的程度，同时颗粒破碎也会造成颗粒级配、形状等的改变。颗粒破碎过程中的形状变化对材料的堆积、摩擦和剪切特性等均产生显著影响[1-2]，但目前对形状演化的规律尚不了解。

为了分析颗粒形状，首先要对其进行测量和表征。测量方法可归结为3类：①静态颗粒二维形状测量[3]，即通过扫描、拍照等方式对静止颗粒的特定断面取像；②动态颗粒二维形状测量[4]，即采用高速摄像机对运动颗粒的断面进行随机捕捉；③三维形状重构[5-6]，即采用断层或激光扫描技术重构颗粒的真实形状。颗粒形状表征也可分为反映颗粒表面凹凸程度的粗糙度、反映颗粒棱角尖锐程度的圆度和反映颗粒三维尺寸相似程度的球度3个尺度[1]。在此基础上，一些学者提出了比较实用的表征指标，比如凸度、纵横比、延伸度和扁平度等[2,4,7]。

利用这些形状指标，国内外学者统计了不同工况下的颗粒破碎形状特征。Zhao等[8]研究了单个颗粒的断裂特征，发现破碎颗粒的形态与颗粒矿物成分、岩性均有关系。Altuhafi等[9]通过一维压缩试验发现初始级配对形状演化具有较大影响，级配良好的颗粒在压缩过程中仅遭受轻微磨圆导致粗糙度降低，而均一粒径颗粒则发生了灾难性的破碎，生成的颗粒形状十分不规则。Zhang等[7]通过均一粒径钙质砂的大位移环剪试验，发现颗粒倾向于变得更加光滑，何建乔等[10]也发现了类似的现象。以上试验均表明，当应力或者剪切应变足够大时，颗粒形状演化会趋于稳定状态，而Yan等[11]对破碎终止的试样进行重构和再加载，发现颗粒依然会破碎，颗粒形状仍会继续变化。

以上研究从整体上把握了颗粒形状的演化趋势，但是无法区分破碎产生的颗粒与未破碎颗粒的形状差异。近年来，有研究者对颗粒进行染色以对破碎颗粒进行示踪，如Nakata等[12]将表面染色的若干颗粒置于三轴试样中，以观察单个颗粒在试样中的断裂特征；彭宇等[13]对钙质砂进行染色，借助图像分割方法对颗粒破碎量进行精细化统计。但是染色的天然颗粒经过多次破碎后可能较难辨别出颜色。为了避免出现以上问题，于际都等[14]提出采用人工制备的染色石膏颗粒进行破碎试验。人工制备的石膏颗粒具有一般岩土颗粒材料的脆性性质，且可以保证颗粒颜色均一，是研究颗粒破碎较为理想的人工材料。在以上研究的基础上，本文借助染色石膏颗粒进一步分析一维压缩破碎过程中的颗粒形状演化。

1 染色石膏颗粒制备

图1 染色石膏颗粒Fig.1 Dyed gypsum particles

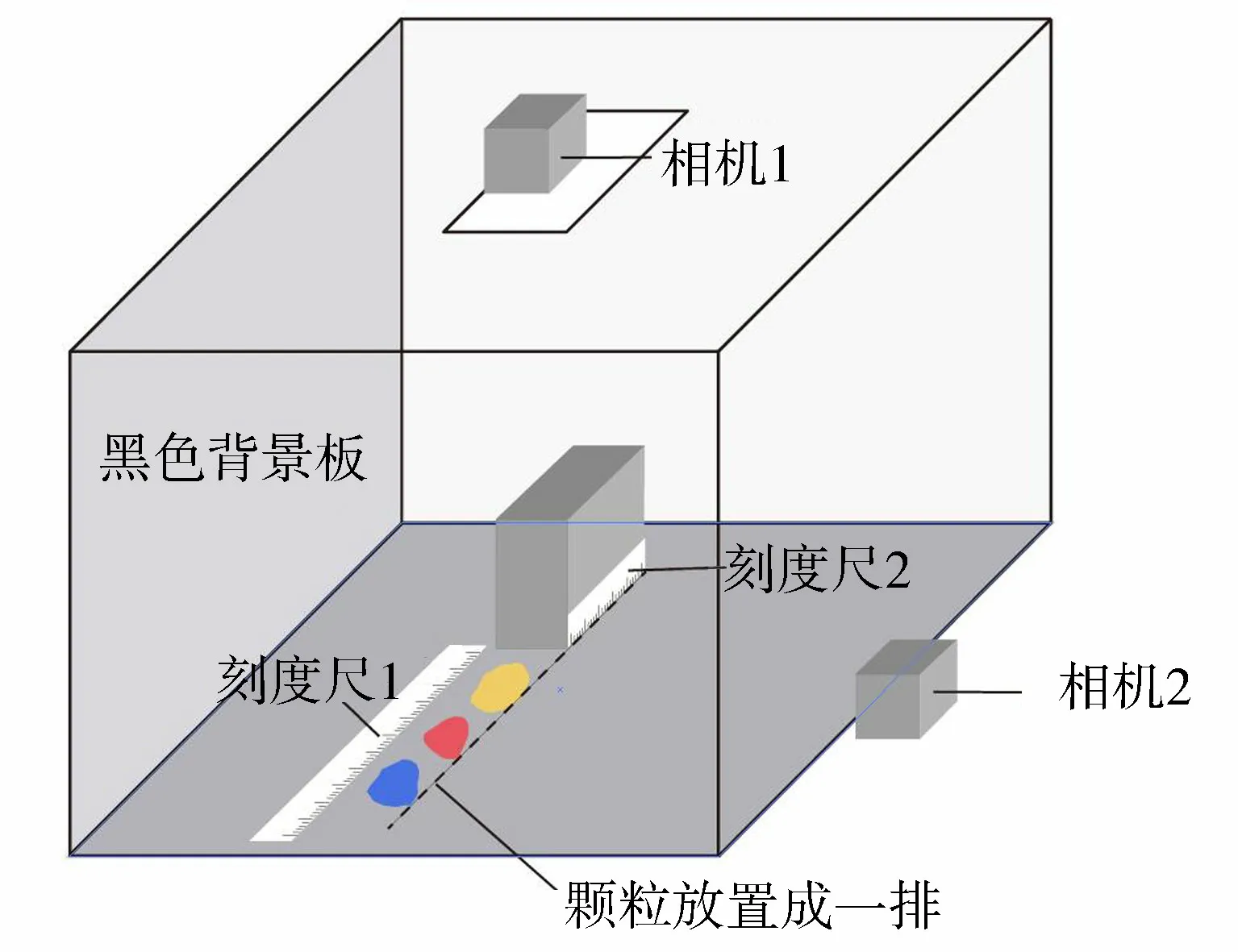
图2 颗粒拍照装置示意图Fig.2 Schematic diagram of particle shape photographing device

2 颗粒形状测量与表征

通过相机拍照获取颗粒的俯视图和侧视图，用以分析颗粒的二维和三维形状特征。图2为颗粒拍照装置示意图，水平和垂直方向各放置一个刻度尺，用于标定颗粒尺寸。ImageJ[4]、Imago[15]、PCAS[16]等程序均可进行图像处理，本文采用自行开发的算法程序进行图像处理，主要步骤如下：①读取图像，根据图像实际尺寸和像素尺寸计算比例尺；②将RGB图转换成灰度图，调整阈值后生成二值图；③提取图像中的连通域，去除面积异常连通域；④根据定义计算连通域形状参数。

本文使用了文献[4]中定义的凸度Cx、圆度S和纵横比AR3个形状因子，并定义了扁平率Fn用于分析颗粒破碎后扁平程度的变化，如图3所示，计算公式分别为

(1)

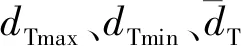
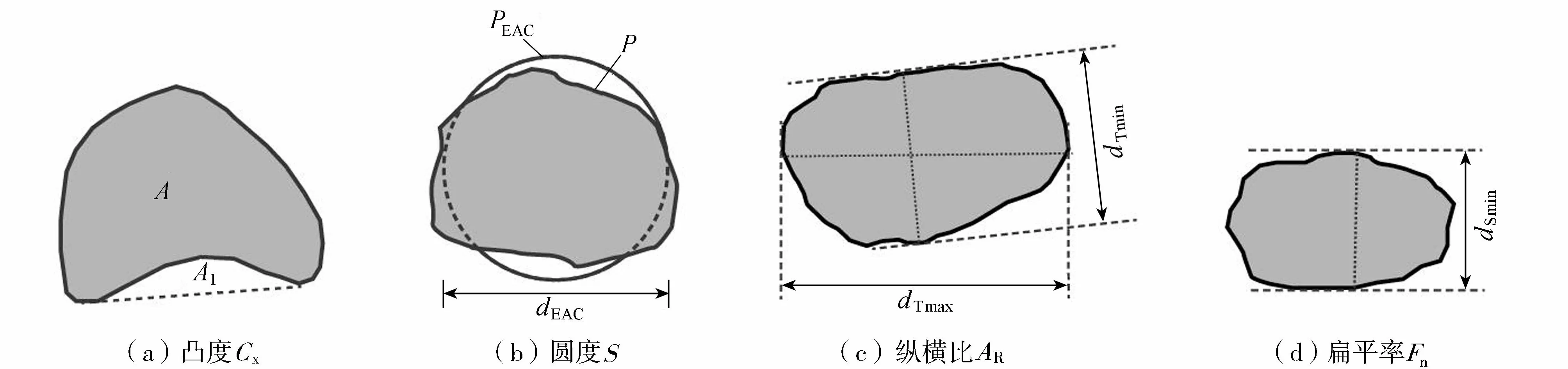
图3 形状因子定义示意图Fig.3 Schematic diagram of the definition of particle shape factors

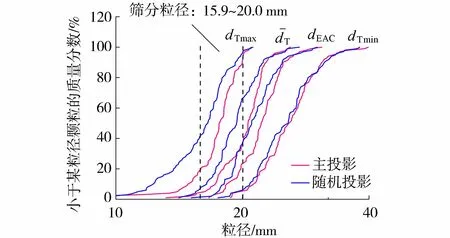
图4 不同颗粒投影面的粒径分析结果Fig.4 Particle size analysis results of different particle projections

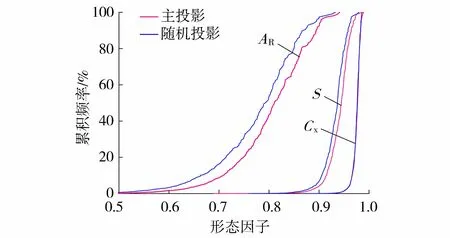
图5 不同颗粒投影面的形状分析结果Fig.5 Particle shape analysis results of different particle projections

3 一维压缩试验

对染色石膏颗粒进行一维压缩试验。测试试样由4种粒径的颗粒各150 g混合而成，共600 g。试样直径为100 mm，高度为75.25 mm，初始孔隙比为1.266。试验以0.5 mm/min的速率加载到6.4 MPa后卸载。对破碎后的颗粒进行筛分，并将同一个粒组中不同颜色的颗粒分开，如图6所示，小于3.1 mm的颗粒因粒径较小暂未统计。定义试验后仍处于原粒径区间的颗粒为存活颗粒，反之称为破碎颗粒。图7为试验前后各粒组颗粒的质量分布。试验后，灰色颗粒破碎产生的子颗粒覆盖所有粒组；而4.0 mm粒组则有全部4种颜色的颗粒，其中黄、红、绿、灰色颗粒的质量分数分别为62%、27%、8%和3%，有62%的颗粒为存活颗粒，其余38%的颗粒由大颗粒破碎产生，显然破碎产生的颗粒占了很大的比例。

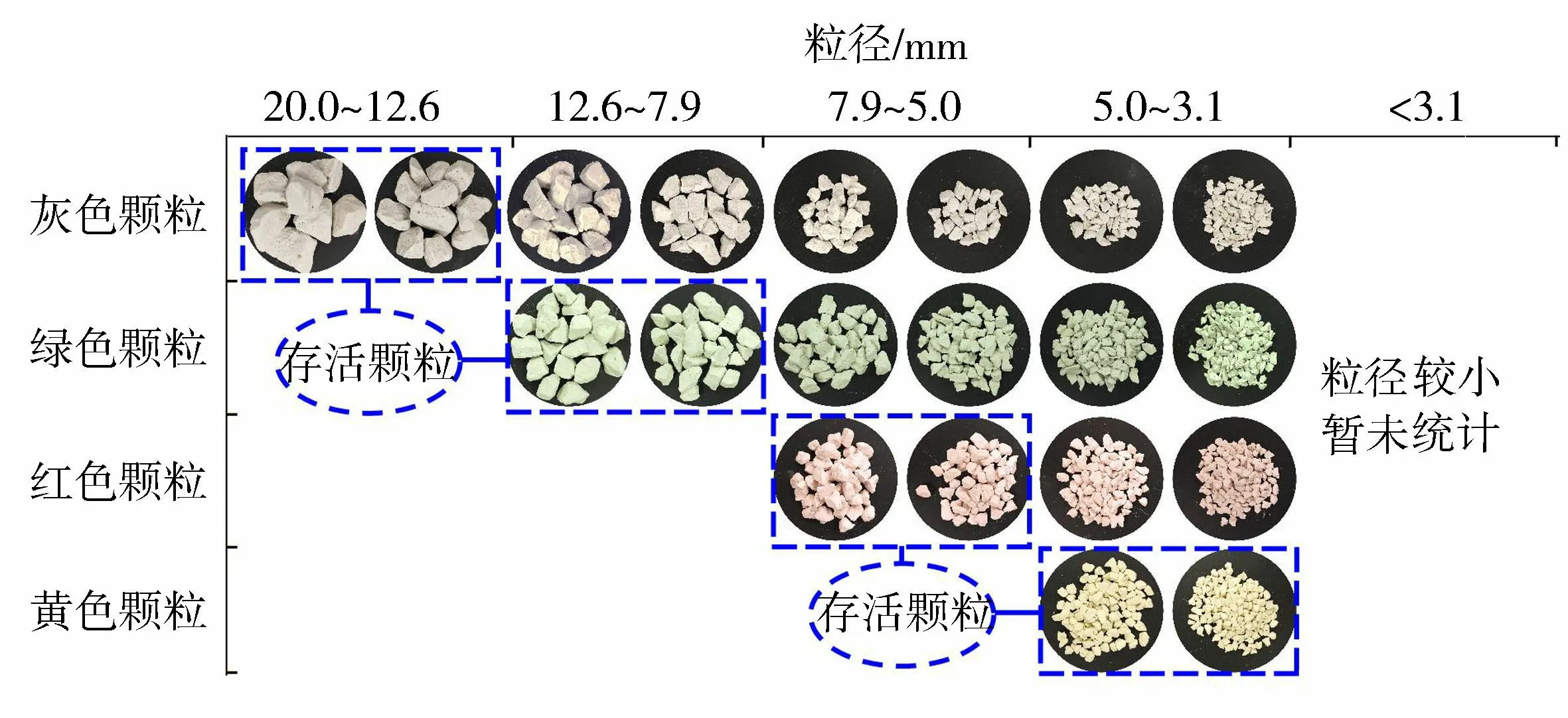
图6 压缩后按照粒径和颜色分离的染色石膏颗粒Fig.6 Dyed gypsum particles separated according to particle size and color after test

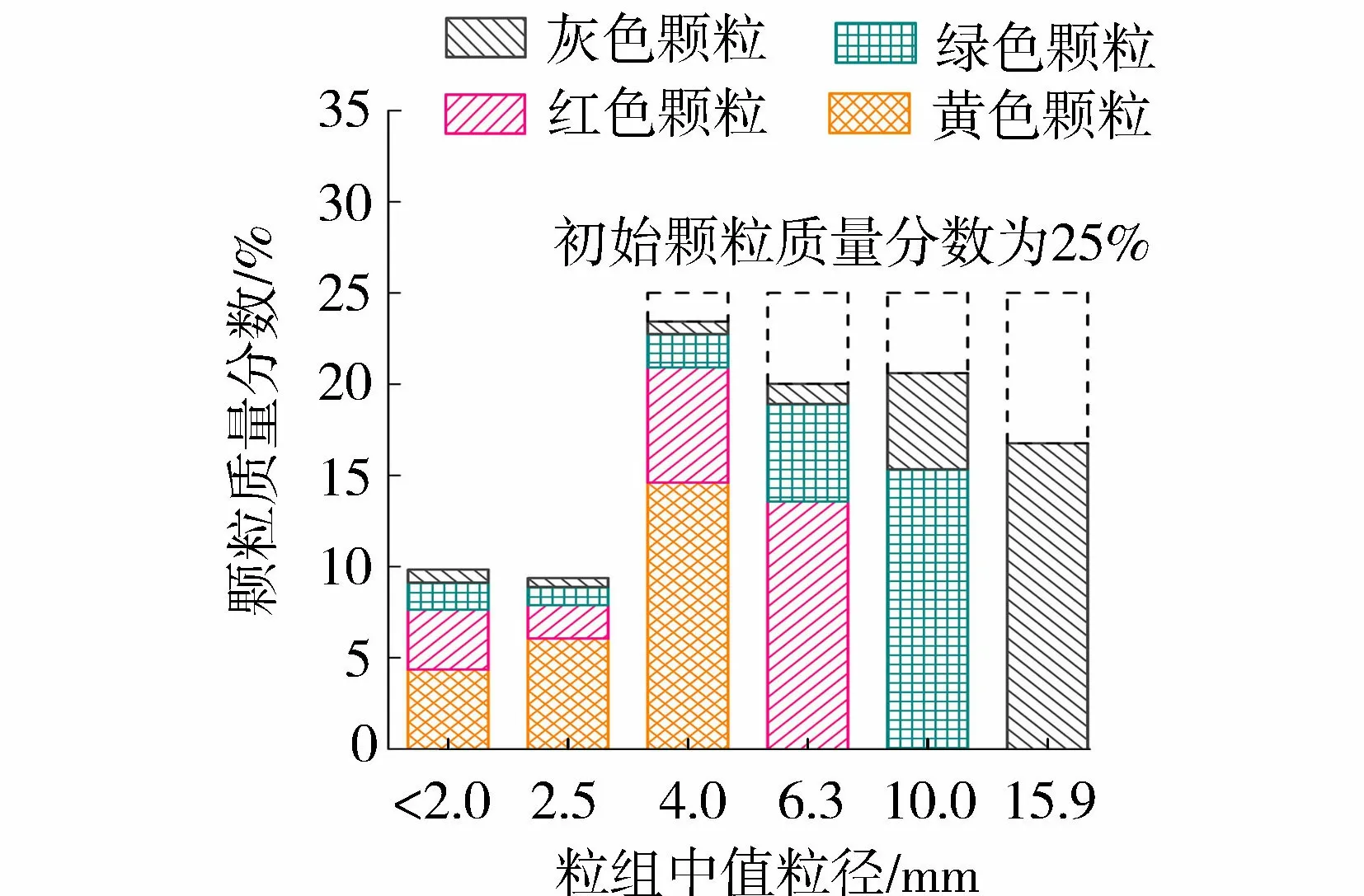
图7 破碎后各粒组颗粒详细的质量分布Fig.7 Detailed mass distribution of particles in each size range after test

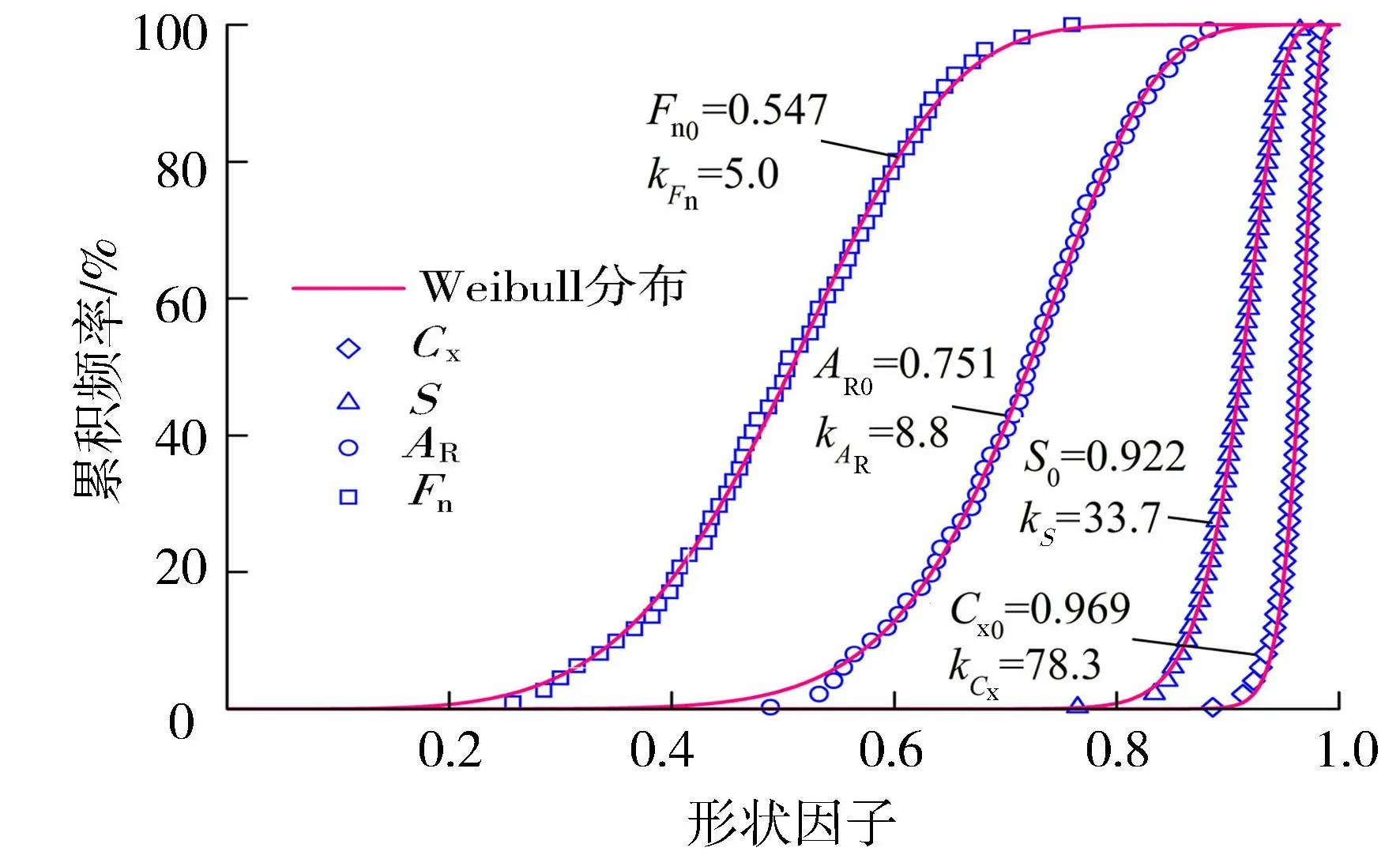
图8 形状因子分布Weibull函数拟合结果Fig.8 Fitting results of the distribution of particle shape factors using Weibull function

4 颗粒形状演化结果分析

4.1 形状因子统计分布

描述形状因子的方式通常有两种，一是用形状因子的平均值，一是绘制频率分布曲线，形如图5所示。采用平均值的方法忽略了形状因子的分布特征，而绘制频率分布曲线过于烦琐，且不便于定量分析。本文采用Weibull函数[17]对形状因子的累积频率分布进行表征：

F(x)=1-exp[-(x/x0)k]

(2)

式中：x为形状因子的值；F(x)为形状因子的累积频率；x0为特征值形状因子，等于63%累积频率下的形状因子；k为Weibull模量，反映形状因子的分布范围，k越大，形状因子的分布范围越小。图8为灰色颗粒形状因子累积频率分布及采用式(1)拟合的结果，拟合值与试验值吻合较好。对初始颗粒和子代颗粒形状因子分布均进行了拟合，相关系数R2均不小于0.966，表明形状因子的统计分布符合Weibull分布。

4.2 形状演化规律分析

图9和图10分别为破碎前后颗粒形状因子大小和分布模量对比。对于初始颗粒，Cx0的取值范围为0.95～0.97，S0为0.92～0.95，AR0为0.74～0.77，Fn0为0.53～0.56；而凸度的Weibull模量kCx为60～80，圆度的Weibull模量kS为25～35，纵横比的Weibull模量kAR为7～9，扁平率的Weibull模量kFn为4.5～5.5。可见，Fn的分布范围最广，AR次之，而Cx和S的差异性并不显著。对比试验前后颗粒的形状特征，发现破碎后粗颗粒的总体形状因子有所增大，而细颗粒的形状因子变化没有明显规律；而破碎后颗粒的k值均高于初始值，即颗粒形状因子的分布范围变窄，意味着同一粒组颗粒形状的差异性降低。很多学者也做过类似的分析，但总的来说破碎后的颗粒整体形状变化趋势并不统一，有些学者认为这和颗粒的初始形状有关[7]。

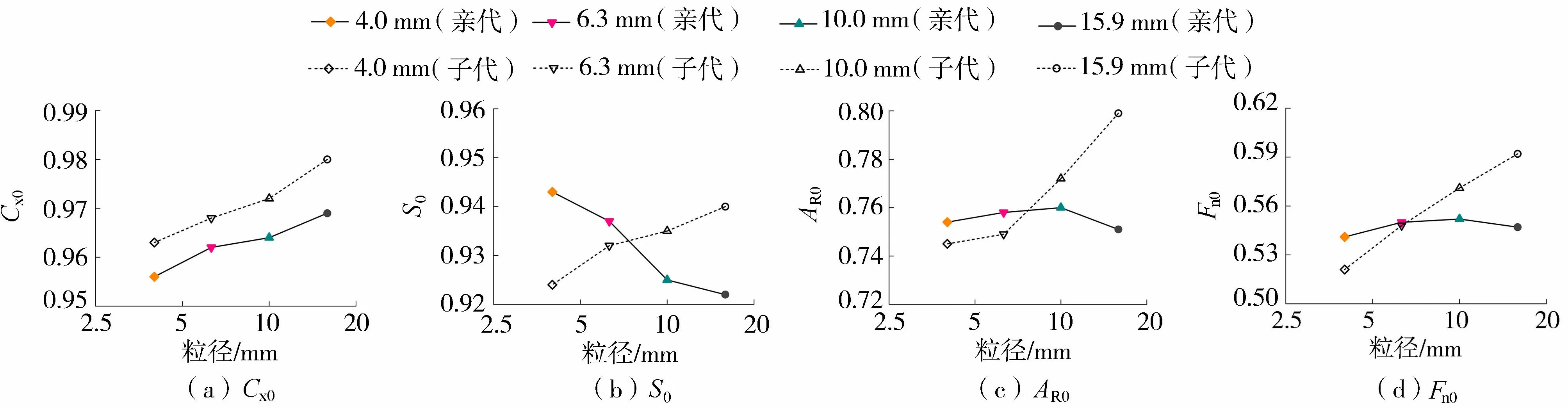
图9 试验前后颗粒的总体特征形状因子Fig.9 Characteristic shape factors of overall particles before and after test

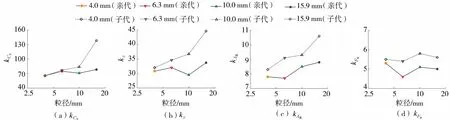
图10 试验前后颗粒的总体形状因子Weibull分布模量Fig.10 Weibull modulus of shape factors of overall particles before and after the test

图11和图12进一步对比了不同亲代颗粒对应的子代颗粒的形状特征，通过分析可以得出以下规律：

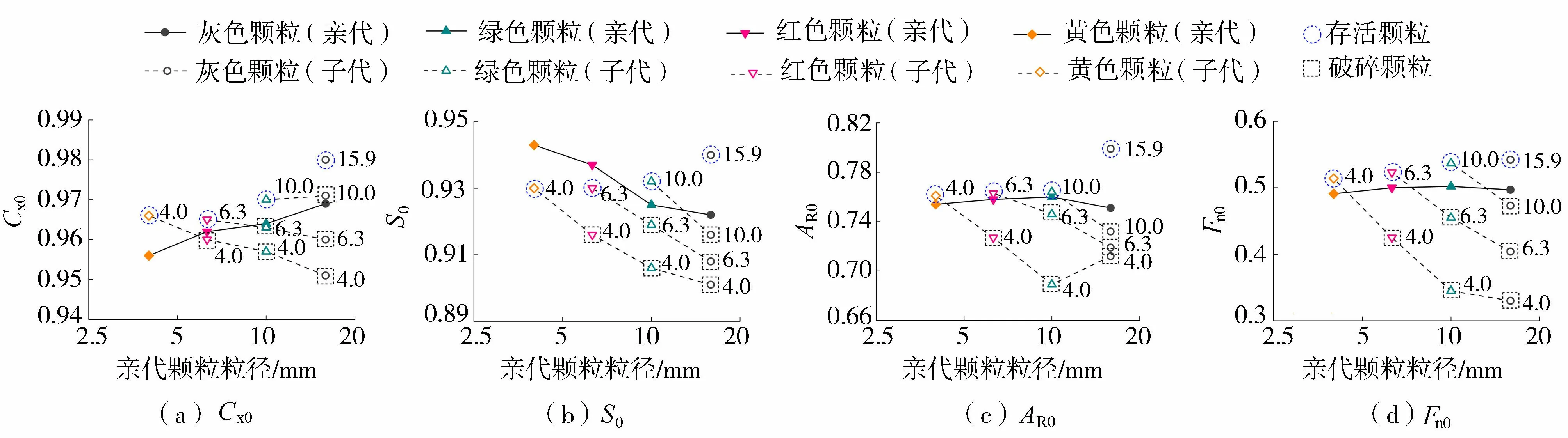
图11 子代颗粒的特征形状因子Fig.11 Characteristic shape factors of child particles

图12 子代颗粒的形状因子Weibull分布模量 Fig.12 Weibull modulus of shape factors of child particles

a.同一亲代颗粒破碎产生的子代颗粒，粒径越小，形状因子越小。即子代颗粒和亲代颗粒粒径差距越大，其表面愈粗糙，圆度愈差，形状愈细长和扁平，且形状分布愈不均一，因为细颗粒可能是经历多次破碎产生的。与Cx和S相比，AR和Fn的变化更为明显，尤其是Fn，比如15.9 mm灰色子代颗粒的Fn(0.592)和4.0 mm灰色子代颗粒的Fn(0.380)相差56%，这主要是因为细颗粒多为粗颗粒应力集中剥落产生，这些剥落的碎片通常呈片状。

b.相同粒径的子代颗粒，其对应的亲代颗粒粒径越大，子代颗粒的形状因子越小。这表明破碎后的颗粒即使处于同一粒径区间，但由于其来源不同，它们的形状产生了明显的差异。图7显示试验后的10.0 mm、6.3 mm和4.0 mm粒组分别有26%、32%和38%的颗粒为来自粗颗粒破碎产生的碎片，这个比例随着粒径区间的减小而增大。细颗粒区间由于接收了更多粗颗粒破碎产生的碎片，其整体形状更容易受到影响，比如图10中6.3 mm和4.0 mm的AR和Fn较初始值有所降低，而颗粒形状因子的改变可能会对颗粒的存活概率造成影响。

c.存活颗粒的形状因子总体上大于其亲代颗粒，而破碎颗粒的形状因子则小于其亲代颗粒。存活颗粒没有发生明显的破碎，因此粒径没有发生明显变化，但由于与周围颗粒的接触摩擦，颗粒表面的棱角被磨圆，直接导致Cx和S增大，并且间接影响了AR和Fn。较大颗粒的磨圆现象更为明显，因为其与更多的颗粒接触。而对于发生破碎的颗粒，它们不仅粒径改变，同时颗粒形状也发生明显劣化，一个显著的变化是颗粒变得更加扁平。

d.形状因子分布模量和形状因子特征值表现出一致的演化趋势。存活颗粒的形状因子分布在一个更窄的范围，因为存活颗粒经过磨圆后表面更光滑且形状更接近球形；而破碎颗粒则可能经过分裂、剥落、磨损等多种碎裂模式产生，因此形态差异更大。

通过以上分析发现，存活颗粒的形状因子增大，而破碎颗粒的形状因子减小。而同一粒组所有颗粒既包含存活颗粒也包含破碎颗粒，其平均形状因子取决于存活颗粒和破碎颗粒的形状及二者的比例。这个比例受很多因素的影响，比如加载的应力、加载的方式、初始颗粒的形状、初始级配、应力水平等，所以颗粒破碎的演化结果不存在确定性，因此出现不同的试样在不同的试验工况下形状演化结果差别较大的现象。

5 结 论

a.子代颗粒与亲代颗粒粒径相差越大，颗粒表面越粗糙、圆度越差、越扁平，且形状因子分布越不均匀。

b.存活颗粒相比亲代颗粒，形状变得更规则，形状因子分布趋向于均一化，而破碎颗粒的形状演化则完全相反。

c.由于整体试样既包含存活颗粒又包含破碎颗粒，其形状演化规律未表现出明显的一致性。