道路雨水口泄流效率关键影响因素研究

段园煜，郭 帅，王秋萍，陈国芬，吴众华，陈 岚

(1.合肥学院城市建设与交通学院，安徽 合肥 230601； 2.合肥工业大学土木与水利工程学院，安徽 合肥 230009； 3.华东勘测设计研究院，浙江 杭州 310014； 4.浙江大学建筑工程学院，浙江 杭州 310058)

道路雨水口是雨水排水系统的组成部分，是路面径流进入地下管道的入口，雨水口的泄流效率直接影响城市路面的积水程度。国家建筑标准设计图集《雨水口(16S518)》[1]指出，雨水口的泄水能力与道路坡度、雨水口形式、箅前水深等因素有关，因此将雨水口的泄流量定为单一值不能满足设计需要。而GB 50014—2006《室外排水设计规范》[2]对雨水口设计的规定不够明确，如仅指出雨水口的布置间距适宜为25～50 m。鉴于此，迫切需要相应的理论或经验公式指导雨水口的优化设计，以提高泄流效率，减少城市内涝的发生[3-4]。

Wong[5]给出了雨水口泄流效率与径流量、道路横纵坡之间的数学关系，但包含了多个未知参数。美国联邦公路局[6]以规范的形式给出了雨水口泄流效率的预测方法，并将流经雨水篦盖周围的径流量分为前端流量和侧边流量，其计算公式包含多个经验参量，计算方法相对烦琐。Spaliviero等[7]和Gómez等[8]分别得出两个关于泄流效率E与径流量和箅前水深比值Qa/h的关系式。Kemper等[9]通过试验得出将偏沟式雨水口泄流效率与弗劳德数、雨水篦子的尺寸以及篦上水深相联系的计算式。除此之外，Li等[10-14]探究了雨水口形式、篦子栅条角度、开孔率等对泄流效率的影响。对于国外文献提出的经验公式，国内还没有进行验证及采纳，但也对雨水口进行了研究。如刘雷斌等[15-16]先用试验方法探究了雨水口泄流效率与径流量及道路纵坡的关系，再用数值模拟方法探究了路面积水深度与雨水口布置间距的关系。梁小光等[17]通过分析国内外道路坡度和雨水口布置的相关要求，结合案例计算，总结了道路横坡、纵坡、箅前水深和雨水口布置间距之间的变化关系，并提出道路设计漫幅的推荐值。陈国芬等[18]用数值模拟方法得出当降雨强度足够大时雨水口的泄流效率将达到饱和的结论。然而，目前国内尚缺乏可以精确计算雨水口泄流效率的经验公式。

本文以《雨水口(16S518)》中的标准型平箅式雨水口为研究对象，探究道路坡度和径流量对泄流效率的影响。基于孔口出流理论，提出泄流效率的计算公式，同时与国外文献中的经验公式进行对比，分析其优劣性，。

1 模型试验概况

1.1 试验平台

雨水口泄流特性研究模型试验平台如图1所示。模拟道路按照1∶1的比例设计，长12 m、宽3 m、侧边高0.5 m，底部铺一层厚10 mm的水泥砂浆，雨水口箅盖安装在距离道路起始端10 m处，模拟一段长12 m、宽6 m水泥道路的一半。千斤顶能调节道路的纵坡范围为0%～5%，横坡范围为0%～10%。试验水由高于模拟道路6 m的水箱提供，由连接在引水箱上的水平导流板均匀地导流进入模拟道路，使进入模拟道路的水流均匀平缓，且能保证重复试验的初始条件一致。试验平台排出的水流入地下水库，用泵实现用水循环。雨水箅盖形式见图2，总开孔面积为0.153 m2，开孔率为54.2%。

图1 试验平台Fig.1 Test platform

图2 雨水口箅盖(单位：mm)Fig.2 Grate cover of street inlet (unit: mm)

表1 试验工况

1.2 试验计算

试验以道路纵坡SL、道路横坡SC和径流量Qa为因变量，探究这3个因素对雨水口泄流效率的影响。道路纵、横坡度的取值参考CJJ 37—2012《城市道路工程设计规范》[19]；根据合肥市的降雨情况，结合汇流面积计算得出径流量的取值范围为0～70 m3/h。

(1)

式中：q为降雨强度，mm/min；P为暴雨重现期，a；t为降雨历时，min。

共进行126组不同工况的试验，见表1。其中，序号1、2各7个工况，流量变化幅度为10 m3/h；序号3～10各14个工况，流量变化幅度为5 m3/h。

2 泄流效率

2.1 试验结果分析

雨水口的泄流效率是指雨水口泄流流量与雨水口上游径流量的百分比：

(2)

式中：Qint为雨水口泄流流量(可分为前缘泄水量和侧边泄水量)；Qa为雨水口上游的径流量，m3/h；Qp为未被雨水口泄流的流量。

在不同坡度条件下，雨水口的泄流效率随径流量的变化如图3所示。由图3可以看出，仅在径流量非常小的情况下(Qa=5 m3/h)，雨水口泄流效率能够达到100%；径流量越大，泄流效率越低。当SC=2.0%、SL=2.0%、径流量从5 m3/h增加到70 m3/h时，泄流效率从100%逐步降低至75%。图3(a)中的3条曲线仅横坡不同，横坡越大，侧向重力对雨水口的有效收水范围影响越大。当横坡从1.0%变为2.0%时，同一流量下的泄流效率约增大20%，当横坡从1.0%增加到1.5%时，其效率的增长梯度大于从1.5%增加到2.0%的情况；在横坡为1.5%时，雨水口的泄流效率已达到较高值(70%～100%)。由图3(b)可知，同一流量下，纵坡在0.3%～5.0%变化时，泄流效率的相对变化约为10%，总体呈现纵坡越大，泄流效率越低的规律。纵坡会改变径流流速的大小，不改变流速方向，其主要通过影响雨水口的前缘泄水量来影响泄流效率。

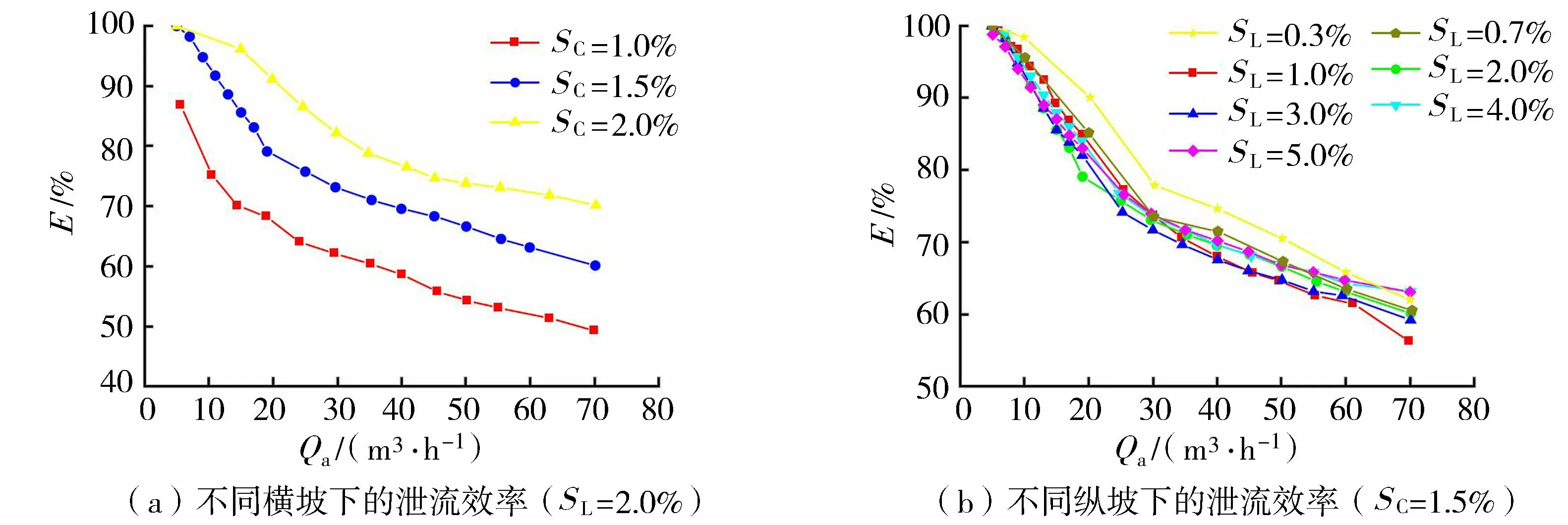
图3 雨水口泄流效率随径流量的变化Fig.3 Variations of inlet efficiencies with runoff

2.2 数据拟合

图4 径流横断面Fig.4 Gutter cross section

在道路横坡的影响下，雨水口箅盖上游的径流横断面形式见图4。雨水均匀流动时，图4中所标参数值保持不变，其中，h为靠近路缘处的水流深度，W为径流覆盖路面的宽度(W>>h，W=h/SC)。各参数间的关系符合谢才公式，则h的表达式可化简为

(3)

路面径流通过雨水口箅盖的开孔泄流，符合孔口出流形式[20-22]，故可用孔口出流方程计算雨水口泄流量(式(4))，进而可得泄流效率E的理论公式(式(5))，式(5)中唯一需要确定的是参数C。

(4)

(5)

式中：n为道路粗糙系数；A0为出流孔口面积，m2；C0、C1、C为泄流系数。

将试验得出的E值代入式(5)计算C，发现C与Qa相关，其关系见图5。由图5可以看出C与Qa具有很高的相关性。去掉实际工程中较少见的4组坡度组合(表1中序号5、6、7、10)，则C的差值在10%以内。相同径流量下，取其余6种坡度下C的均值，拟合其与Qa的数学关系，结果见图6，表达式为

C=2.3Qa0.574

(6)

图5 实测C值与Qa关系Fig.5 Relationship between measured C and Qa

图6 C的实测值与预测值的对比Fig.6 Comparison of measured C and predicted C

则标准型平箅式雨水口的E计算式为

E=2.3Qa-0.239SC0.187 5SL-0.094

(7)

由式(7)可知，E主要的影响因素有径流量、横坡和纵坡，且受径流量和横坡的影响程度大于纵坡。

为校验式(7)的准确性，取SL=1.5%、SC=1.2%和SL=0.8%、SC=1.7%进行验证，其结果见图7(a)，可见E的计算值与实测值符合度较高。

图7 试验与计算所得E的对比Fig.7 Comparison of E by formula calculation and experimental measurement

一些国外研究通过试验提出了雨水口泄流效率的经验公式，英国水力实验室提出的公式为[7]

(8)

式中：G为雨水箅子综合几何参数；Ag为箅子面积，m2；p为孔隙率；nt、nl、nd分别为横格条数、纵格条数和斜格条数。

Gómez等[8]提出的公式见式(9)。用式(8)、式(9)试验数据校验，结果见图7(b)。

(9)

式中：L为雨水箅子长度，m；W为雨水箅子宽度，m。

由图7(b)可见，式(8)在Qa/h< 0.5 m2/s时，计算的泄流效率与实测值较接近；当Qa/h> 0.5 m2/s时，偏离越来越大。式(9)则更适用于计算Qa/h>0.3 m2/s的情况(当Qa/h<0.3 m2/s时，式(9)计算的E均大于100%)。式(8)的拟合相关指数R2=0.853，式(9)的R2=0.881，即式(9)比式(8)更符合实测数据的散点分布。对比图7(a)和图7(b)，对于图2所示的雨水口，图7(a)的拟合效果(R2=0.99)远高于图7(b)；但对于其他平箅式雨水口，在C未知的情况下，式(9)可用来大致估计E。

3 雨水口布置间距

综合上述分析，标准型平篦式雨水口宜优先采用式(7)进行优化设计；若为其他类型雨水口，在当前缺乏原始试验数据的情况下，推荐采用式(9)[8]进行设计。

雨水口能有效排水的定义是在设计暴雨重现期下其泄流效率大于一定值(根据试验数据，可取50%～70%)，则根据对雨水口泄流效率的分析，各雨水口设计间距的计算式为

(10)

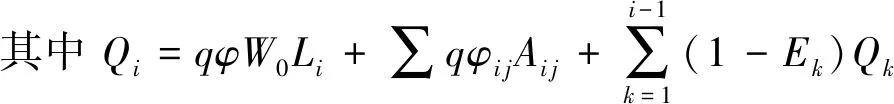
Ei=2.3Qi-0.239SC0.187 5SL-0.094

式中：Qi为第i个雨水口上游的径流量，m3/h；Ei为第i个雨水口的泄流效率；Li为第i个雨水口距离道路起始端的设计间距，m；W0为道路总宽度的一半，m；φ为路面径流系数；φij、Aij分别为第i个雨水口汇流区扣除上游道路面积W0Li后第j个汇流分区的径流系数和面积。

根据以上间距设计公式，越往下游雨水口设计间距应越小，为了道路美观及雨水口布置的简便，雨水口一般等间距设计，则：

L=(L1+L2+…+Ln)/n

(11)

4 结 论

a.雨水口泄流效率受径流量、横坡、纵坡的影响，随纵坡和径流量的增大而减小，随横坡的增大而增大，其中受径流量和横坡的影响更显著。

b.结合曼宁公式与孔口出流公式，并根据标准雨水口的试验数据，给出泄流效率的拟合公式；公式中的泄流系数与雨水口上游的径流量相关，当道路纵坡为0.3%～3.0%、横坡为1.0%～2.0%时，系数值几乎不随坡度变化。

c.根据研究所得泄流效率的计算公式，给出了雨水口布置间距的计算方法；在连续坡度道路上，越往下游，雨水口承担的泄流任务越大，故在下游宜将雨水口布置成双箅、多箅来提高下游排水效率。